Самостоятельная работа по дисциплине Теория расчета пластин и оболочек по шифру 180323
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Саратовский Государственный Технический Университет имени Гагарина Ю.А.» Кафедра: «Строительные материалы, конструкции и технологии» САМОСТОЯТЕЛЬНАЯ РАБОТА по дисциплине: «Теория расчета пластин и оболочек» по шифру №180323 Подготовил: студент группы с1-СЗС31 ___________Торопова Н.А. Принял: акад. РААСН, д.т.н. профессор ___________ Петров В.В. Саратов 2021 г Задание №1Для пологой оболочки (положительной, отрицательной или нулевой гауссовой кривизны) на прямоугольном плане размерами 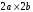 , а=4м, b=4м выполненной из линейно-упругого материала с коэффициентом Пуассона , а=4м, b=4м выполненной из линейно-упругого материала с коэффициентом Пуассона 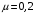 и расчетным сопротивлением и расчетным сопротивлением 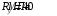 и действующей равномерно распределенной нагрузкой интенсивностью и действующей равномерно распределенной нагрузкой интенсивностью 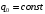 требуется: требуется:Описать схему, предложенную в варианте (тип оболочки, форма, тип граничных условий и т.д.). Записать уравнение поверхности переноса в соответствии с заданными радиусов кривизн контурных линий, через общее уравнение окружности в плоскости 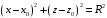 . .Определить коэффициенты первой и второй квадратичной формы поверхности. Определить индикатрису Дюпена (сделать вывод о типе поверхности). Определить кривизну нормального сечения при 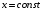 и и 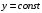 (главные кривизны). (главные кривизны).Рассчитать среднюю и Гауссову кривизну поверхности. В соответствии с заданными условиями на контуре пологой оболочки построить аппроксимирующие функции для прогиба 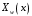 и и 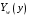 и для функции усилий и для функции усилий 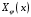 и и 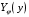 статическим методом В.З. Власова. статическим методом В.З. Власова.Записать вариационные уравнения метода Бубнова-Галеркина для системы разрешающих уравнений тонкой пологой оболочки. Вычислить величины определенных интегралов и подсчитать величины коэффициентов 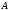 и и 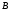 в функциях в функциях 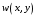 и и 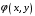 . .Записать выражения для функций изгибающих моментов 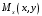 и и 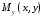 , крутящего момента , крутящего момента 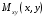 и мембранных усилий и мембранных усилий 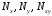 . .Построить эпюры прогибов 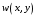 и моментов и моментов 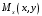 и и 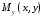 ; эпюры функции усилий ; эпюры функции усилий 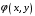 и осевых сил и осевых сил 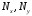 в серединных сечениях пологой оболочки. в серединных сечениях пологой оболочки.Определить наибольшую величину интенсивности напряжений в центре пологой оболочки и подсчитать максимальную нагрузку на оболочку при которой выполняется условие 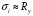 . .Исходные данныеВариант схемы № 2. (см. рис.1) Радиус вдоль оси х Rx=90 Радиус вдоль оси y Ry=80 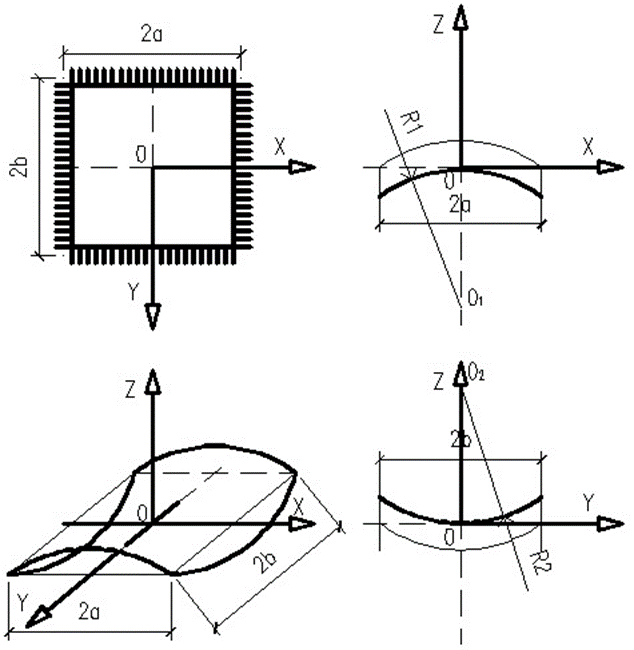 Рисунок 1.Схема №2 1. Описать схему, предложенную в варианте (тип оболочки, форма, тип граничных условий и т.д.).Схема тонкостенной пространственной конструкции, представленной на рисунке, является двояковогнутой оболочкой, отрицательной Гаусовой кривизны. Нагрузка на оболочку равномерно распределенная, следовательно, симметрия по нагрузке присутствует в любом направлении. В направлении оси х, граничные условия симметричные: сверху и снизу имеется жесткая заделка; в направлении оси y, граничные условия симметричные: слева и справа жесткая заделка. По приведенному описанию оболочки можно расположить точку начала декартовой системы координат, в левом верхнем углу оболочки. Граничные условия для приведённой пластинки приведём в символьном виде. 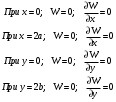 2. Записать уравнение поверхности переноса в соответствии с заданными радиусов кривизн контурных линий, через общее уравнение окружности в плоскости 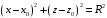 Заданные радиусы кривизн: Rx=90; Ry=80 Уравнение поверхности переноса имеет вид 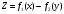 Для построения поверхности переноса воспользуемся данными приведенными на рис.1. рассмотрим плоскость XOZ, в которой общее уравнение имеет вид 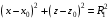 . .Поскольку начало координат по оси x расположено в левом углу оболочки, то имею следующие условия: 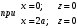 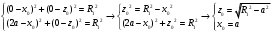 Получаем уравнение края оболочки переноса, расположенного в плоскости XOZ 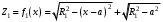 Рассмотрим плоскость XOY, в которой общее уравнение имеет вид 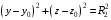 Поскольку начало координат по оси x расположено в левом углу оболочки, то имею следующие условия: 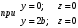 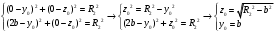 Получаем уравнение края оболочки переноса, расположенного в плоскости XOY 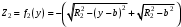 Совмещая полученные уравнения для обоих направлений получим следующее уравнение для поверхности переноса: 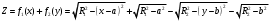 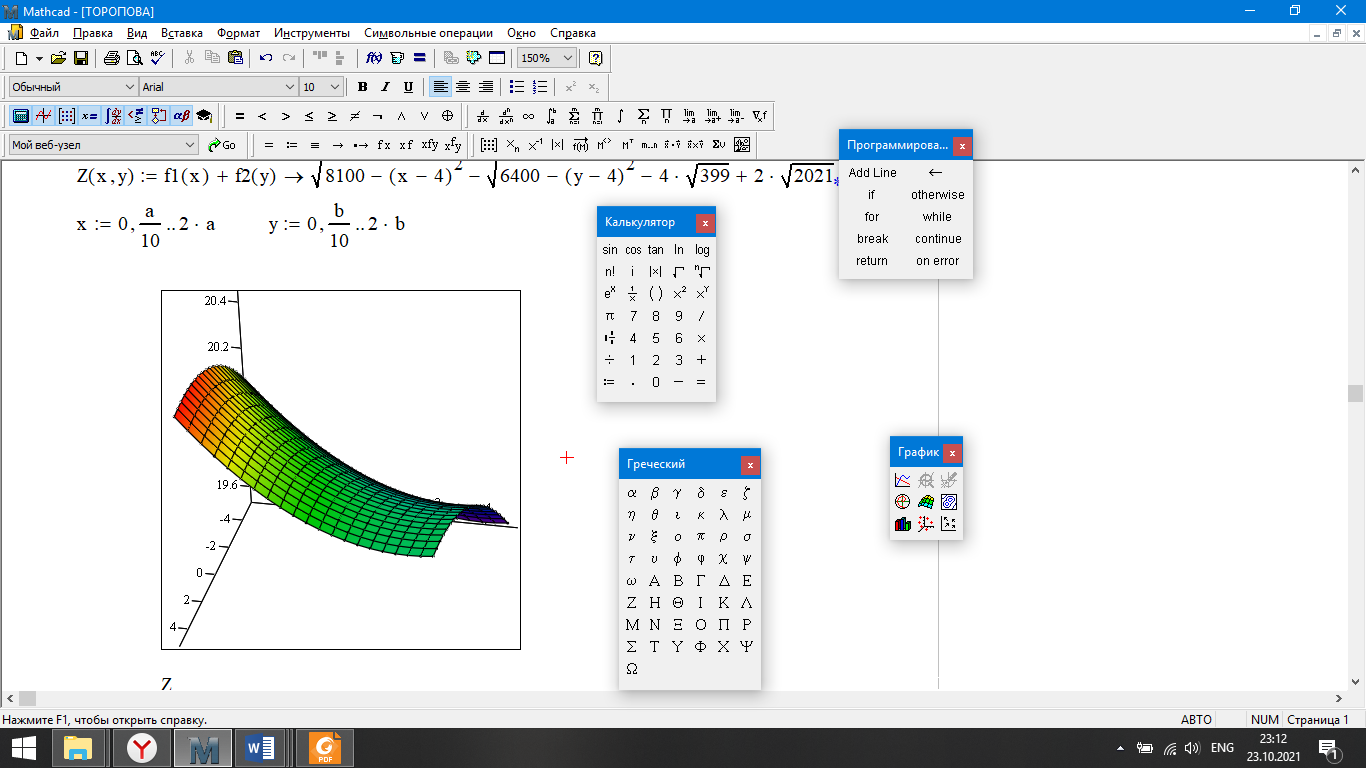 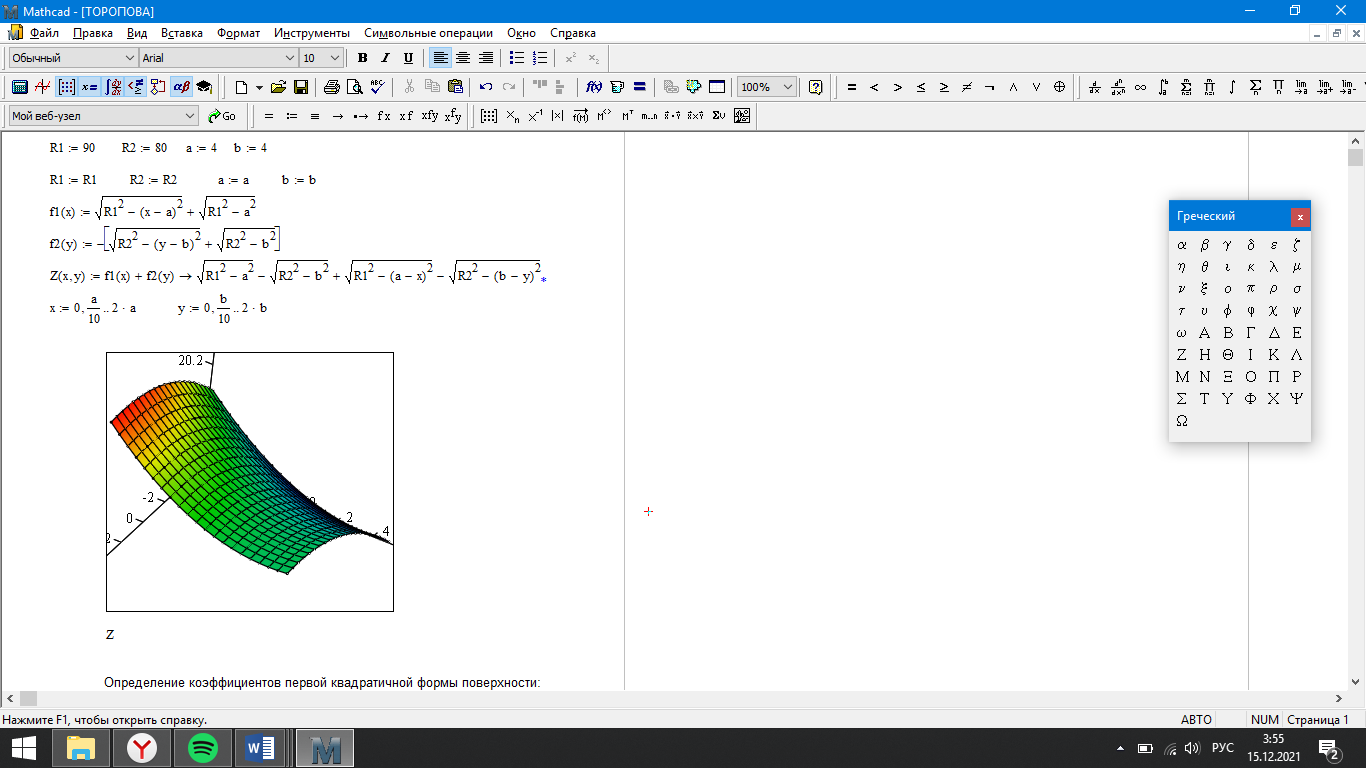 Рисунок 2. Поверхность переноса 3. Определить коэффициенты первой и второй квадратичной формы поверхности.Значения коэффициентов первой квадратичной формы поверхности вычисляются по формуле 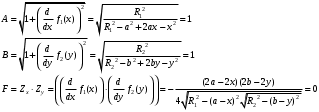 Значения коэффициентов второй квадратичной формы поверхности вычисляются по формуле 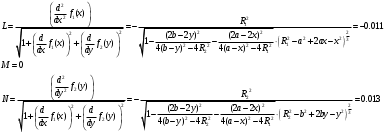 4. Определить индикатрису Дюпена (сделать вывод о типе поверхности).Определения величины индикатрисы Дюпена, определяющее уравнение 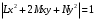 Вид кривой определяется в зависимости от значения инварианта 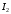 : :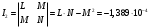 Величина I2< 0, значит индикатриса представляет собой пару смежных гипербол. 5. Определить кривизну нормального сечения при 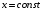 и и 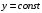 (главные кривизны). (главные кривизны). Кривизна нормального сечения 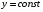 : :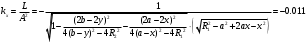 Кривизна нормального сечения 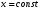 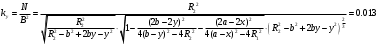 6. Рассчитать среднюю и Гауссову кривизну поверхности.Гауссова кривизна поверхности 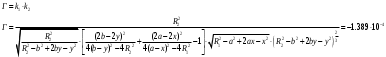 Средняя кривизна поверхности 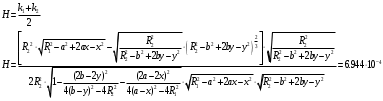 7. Построение аппроксимирующий функций для прогиба и для функции усилий статическим методом В. З. Власова.В соответствии с заданными условиями на контуре пологой оболочки построить аппроксимирующие функции для прогиба и для функции усилий статическим методом В.З. Власова. Граничные условия для функции прогиба: 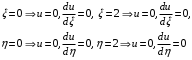 Граничные условия для функции усилий: 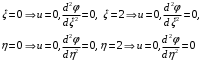 Запишем уравнение для функции прогиба в направлении оси 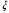 : :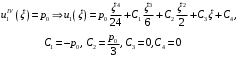 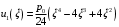 Запишем уравнение для функции прогиба в направлении оси 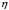 : :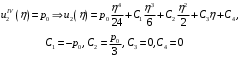 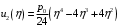 Запишем уравнение для функции усилий в направлении оси 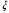 : :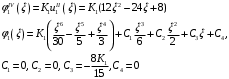 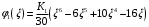 Запишем уравнение для функции усилий в направлении оси 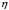 : :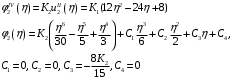 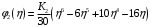 Итоговые функции: 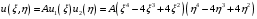 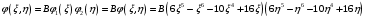 8. Записать вариационные уравнения метода Бубнова-Галеркина для системы разрешающих уравнений тонкой пологой оболочки:Запишем систему дифференциальных уравнений для пологих оболочек в безразмерном виде: 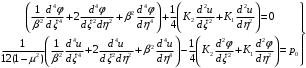 Используя приведенную систему уравнений для пологой оболочки записываем вариационное уравнение метода Бубнова-Галеркина и приводим определенные интегралы в качестве коэффициентов: 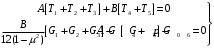 9. Вычислить величины определенных интегралов и подсчитать величины коэффициентов 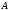 и и  в функциях в функциях  и и  . . Коэффициенты данной системы вычисляются в следующем виде:  Вычисляем величины определенных интегралов и величины коэффициентов А и B: 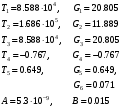 10. Записать выражения для функций изгибающих 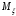 , ,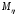 и крутящего и крутящего 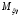 моментов, мембранных усилий моментов, мембранных усилий  , , , поперечных сил , поперечных сил  , , . .  11. Построить эпюры прогибов  и моментов и моментов  и и  , осевых сил , осевых сил  , , и поперечных сил и поперечных сил  , , в серединных сечениях пологой оболочки. в серединных сечениях пологой оболочки. Рисунок 3. Эпюры прогиба по оси  и и   Рисунок 4. Эпюры моментов по оси  и и   Рисунок 5. Эпюры поперечных сил по оси  и и   Рисунок 6. Эпюра осевых сил по оси  и и  12. Определить наибольшую величину интенсивности напряжений в центре пологой оболочки и подсчитать максимальную нагрузку на оболочку при которой выполняется условие 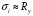 . .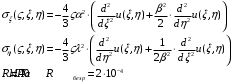  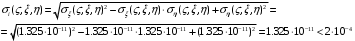 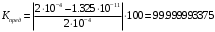 Оболочка недогружена на 99,999%. |
