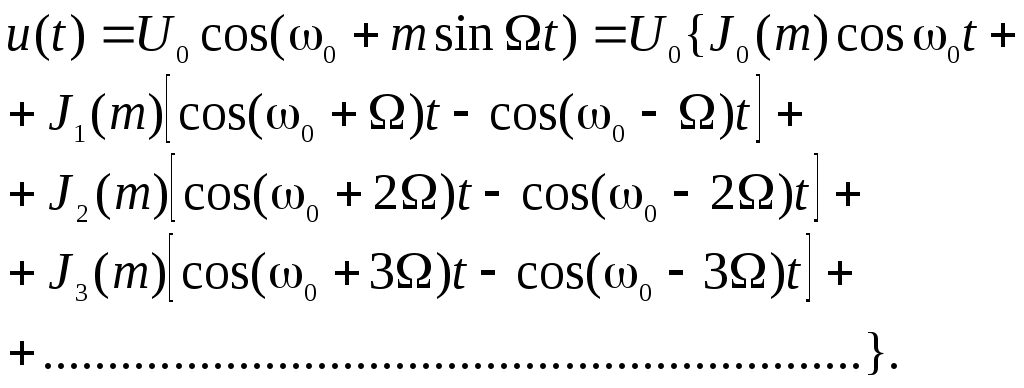МетодаАСПИ (1). Санктперербургский государственный университет аэрокосмического приборостроения
 Скачать 451.5 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования САНКТ-ПЕРЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ _______________________________________________________________ АМПЛИТУДНАЯ И ЧАСТОТНАЯ МОДУЛЯЦИЯ Методические указания к выполнению лабораторных работ по дисциплине «Аппаратные средства передачи информации» Санкт-Петербург 2015 Составитель С. И. Зиатдинов Рецензент кандидат технических наук В. И. Исаков Методические указания содержат описание двух лабораторных работ по курсу "Аппаратные средства передачи информации". Изучаются временные и частотные характеристики амплитудно - и частотно - модулированных сигналов. Предназначены для студентов специальности информационных специальностей. Подготовлены кафедрой информационно-сетевых технологий и рекомендованы к изданию редакционно-издательским советом университета. Сдано в набор Подписано к печати Формат 60х84 1/16. Бумага офсетная. Печать офсетная. Усл.печ.л. Тираж экз. Заказ № Редакционно-издательский центр ГУАП 190000, Санкт-Петербург, Б. Морская ул., 67 СПбГУАП, 2015 Лабораторная работа №1 ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК АМПЛИТУДНО-МОДУЛИРОВАННЫХ СИГНАЛОВ Цель работы: расчет и построение амплитудно-модулированных сигналов и их спектров. 1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Основным назначением различных аппаратных средств передачи информации является передача сообщений о каком-либо событии на расстояние. Расстояние разделяет отправителя и адресата сообщения и может быть очень незначительным (передача информации в пределах ЭВМ от одного блока к другому) или огромным (межконтинентальная или космическая связь). Передача сообщений осуществляется посредством проводных, кабельных, волноводных, оптоволоконных линий или свободного пространства (воздушной среды, космического пространства). При этом в качестве переносчика информации используются электрические сигналы, которые подвергаются модуляции. Процесс модуляции заключается в том, что достаточно высокочастотные электрические колебания наделяются признаками, однозначно характеризующими полезное сообщение. Для этого один (или несколько) параметр высокочастотного колебания изменяется по закону, совпадающему с законом изменения передаваемого сообщения. В зависимости от изменяемого параметра (амплитуды, частоты или фазы колебания) различают три основных вида модуляции – амплитудную, частотную и фазовую. Обратное преобразование модулированных высокочастотных колебаний в первоначальный сигнал, осуществляемое на приемной стороне, называется демодуляцией или детектированием, соответственно, амплитудным, частотным или фазовым. Амплитудная модуляция является наиболее простым и очень распространенным способом заложения информации в высокочастотное колебание. При амплитудной модуляции огибающая амплитуд несущего колебания изменяется по закону, совпадающему с изменением передаваемого сообщения, частота же и начальная фаза колебания остаются неизменными. Поэтому для амплитудно-модулированного колебания можно общее выражение записать следующим образом:
где  ,  ,  ,  – мгновенное значение, амплитуда, частота и начальная фаза колебания.При этом амплитуда определяется видом передаваемого сообщения  .Пусть передаваемое сообщение , являющееся модулирующей функцией, представляется гармоническим колебанием
где  ,  ,  – амплитуда, частота и начальная фаза модулирующей функции.Амплитуда модулированного колебания при этом может быть записана
где  ;  – коэффициент пропорциональности;  – среднее значение амплитуды.Перепишем соотношение (2) следующим образом:
Отношение  называется коэффициентом глубины амплитудной модуляции или просто коэффициентом модуляции.Таким образом, мгновенное значение модулированного колебания можно записать в форме
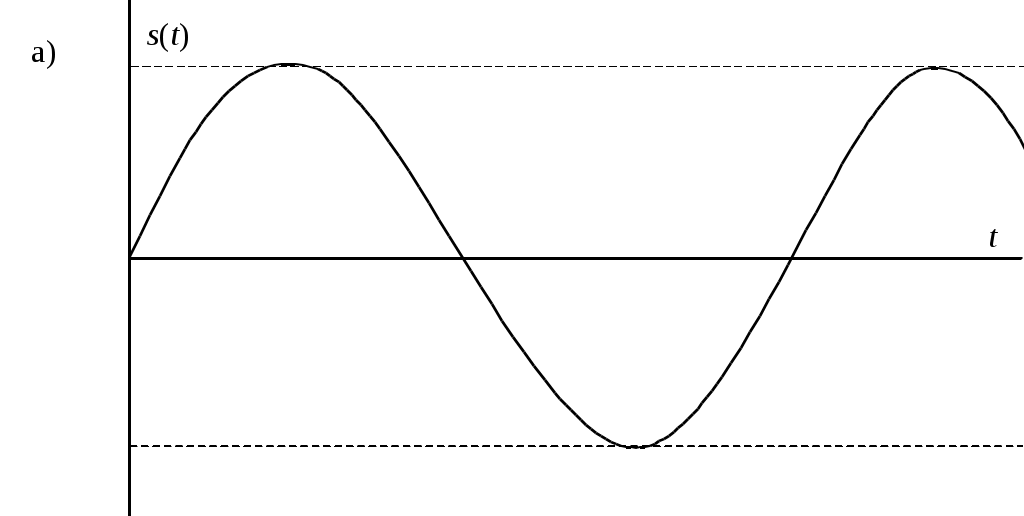
На рис. 1, а показан модулирующий сигнал , на рис.1, б – сигнал .
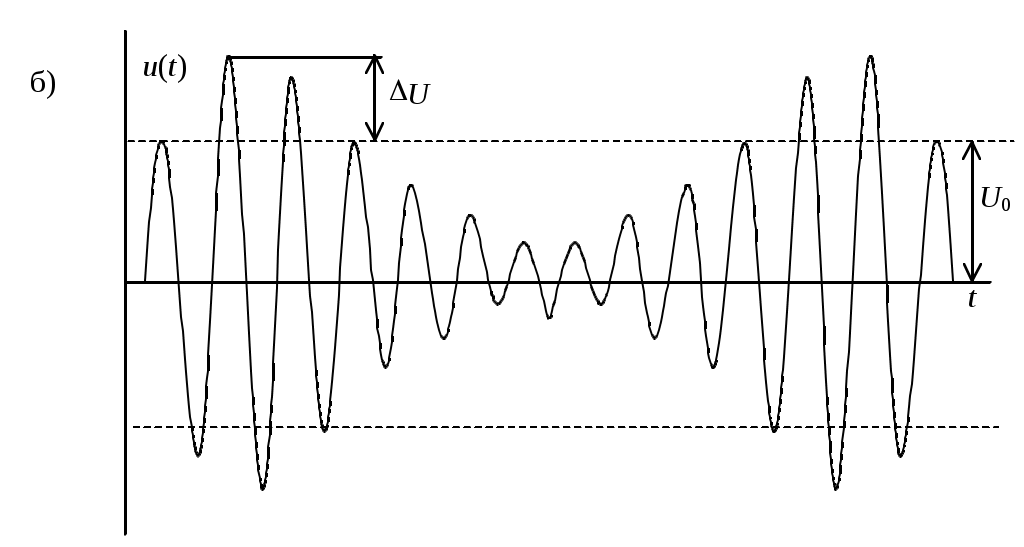
При неискаженной модуляции (  ) амплитуда колебания изменяется от минимальной  до максимальной  .В соответствии с изменением амплитуды изменяется и средняя за период высокой частоты мощность модулированного колебания. Пикам амплитуды соответствует мощность, в  раз большая, чем мощность несущего колебания. Средняя же за период модуляции мощность пропорциональна среднему квадрату амплитуды :
где черта над функцией означает операцию усреднения по времени. Таким образом, при стопроцентной модуляции (  ) пиковая мощность равна 4 , а средняя мощность 1,5 ( ) – мощность несущего колебания. Отсюда видно, что обусловленное модуляцией приращение средней мощности колебания, которое в основном и определяет условие выделения сообщения при приеме, и при предельной глубине модуляции не превышает половины мощности несущего колебания.Частотный спектр амплитудно-модулированного сигнала при гармонической модуляции Для нахождения спектра амплитудно-модулированного колебания в случае тональной (гармонической) модуляции запишем соотношение (4)
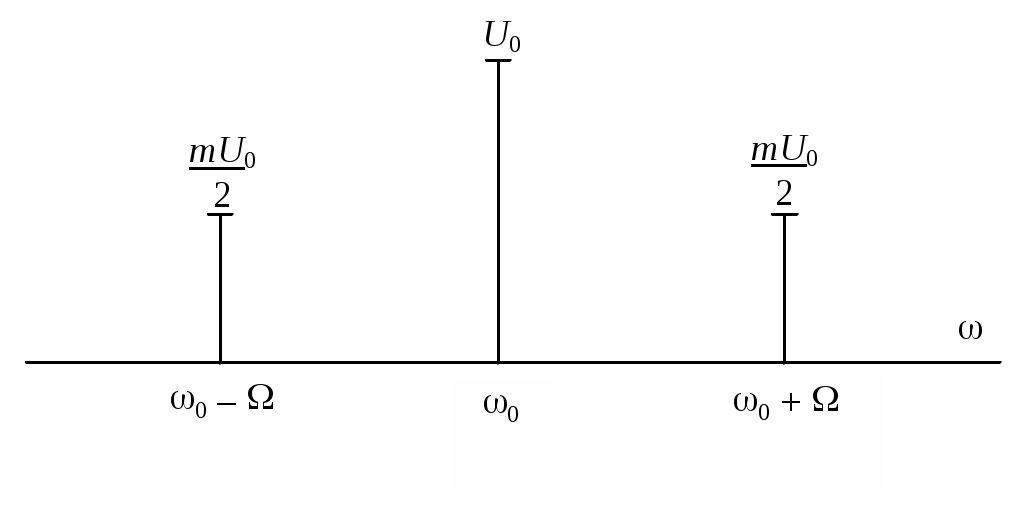
Второе слагаемое в правой части этого выражения, являющееся продуктом модуляции, может быть приведено к форме
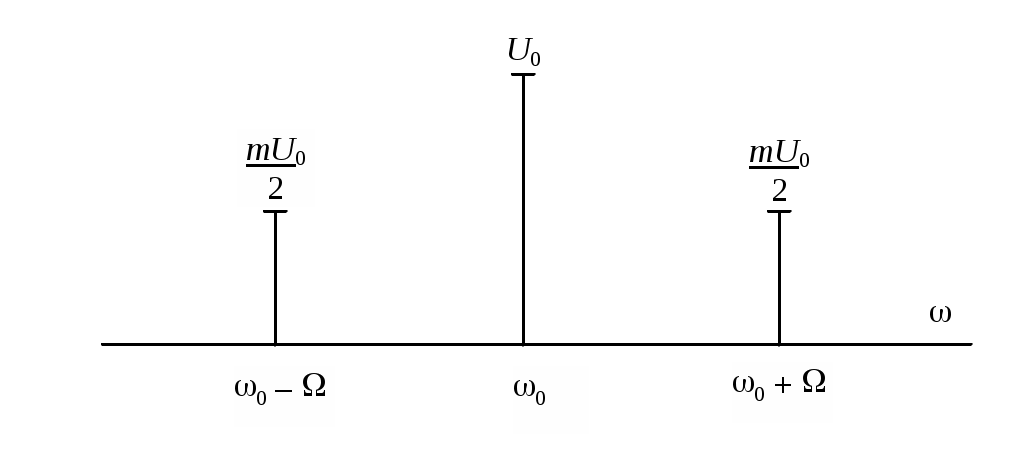
При этом развернутое выражение колебания принимает вид
Первое слагаемое в правой части представляет собой исходное немодулированное колебание с «несущей» частотой  . Второе и третье слагаемые соответствуют новым колебаниям (гармоническим), появляющимся в процессе модуляции амплитуды. Частоты этих колебаний  и  называются «верхней» и «нижней» боковыми частотами модуляции.Амплитуды этих двух колебаний одинаковы и составляют от амплитуды немодулированного колебания долю, равную  /2, а их фазы симметричны относительно фазы несущего колебания.Спектральная диаграмма колебания при тональной модуляции показана на рис. 2.
2. ПОРЯДОК ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ 1. Представить основные теоретические положения, связанные с амплитудной модуляцией. Привести математические формулы для мгновенных значений модулирующего, несущего и модулированного сигналов. 2. Представить основные теоретические положения по расчету спектров амплитудно-модулированных сигналов в случае модуляции гармоническим сигналом. 3. В соответствии с вариантом задания изобразить вручную или на экране ПК временные реализации модулирующего и несущего сигналов. 4. В соответствии с вариантом задания изобразить вручную или на экране ПК амплитудно-модулированное гармоническим сигналом колебание для трeх значений коэффициента модуляции M = 10, 50 и 100%. 5. Для каждой из реализаций рассчитать и изобразить вручную или на экране ПК спектр амплитудно-модулированного сигнала. . 3. ЗАДАНИЯ ______________________________________________________________________
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Сов. радио, 1971. Лабораторная работа №2 ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК СИГНАЛОВ ПРИ УГЛОВОЙ МОДУЛЯЦИИ Цель работы: моделирование с помощью ЦВМ, расчет и построение спектральной плотности частотно-модулированных сигналов. 1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ При угловой модуляции информация о событии закладывается либо в мгновенную частоту (частотная модуляция), либо в мгновенную фазу (фазовая модуляция) несущего колебания. Запишем выражение для высокочастотного несущего колебания
где  – мгновенная фаза колебания. При этом мгновенная частота колебания
Одновременно мгновенная фаза записывается следующим образом
Из соотношений (2) и (3) следует, что изменение фазы колебания по закону  приводит к изменению мгновенной частоты по закону производной от , а изменение мгновенной частоты по закону  приводит к изменению фазы по закону интеграла .Рассмотрим случай простейшей гармонической частотной модуляции, когда мгновенная частота колебания определяется выражением
где = 2f представляет собой амплитуду частотного отклонения (девиация частоты или просто девиация). Через 0,, как и в случае амплитудной модуляции, обозначены несущая частота и модулирующая частота. Составим выражение для мгновенного значения несущего колебания, частота которого изменяется по закону (4), а амплитуда постоянна. Подставляя в (3) из уравнения (4), получаем
Таким образом
Фаза колебания наряду с линейно возрастающим слагаемым  содержит еще периодическое слагаемое  . Это позволяет рассматривать как колебание, модулированное по фазе. Закон этой модуляции является интегральным по отношению к исходной частотной модуляции. Изменение частоты по закону  приводит к изменению фазы по закону .Амплитуду изменения фазы
называют индексом угловой модуляции. Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты 0, а определяется исключительно величиной девиации и модулирующей частотой . Рассмотрим теперь гармоническую фазовую модуляцию, когда мгновенная фаза изменяется по закону
При этом
Найдем частоту этого колебания. Применяя выражение (2), находим
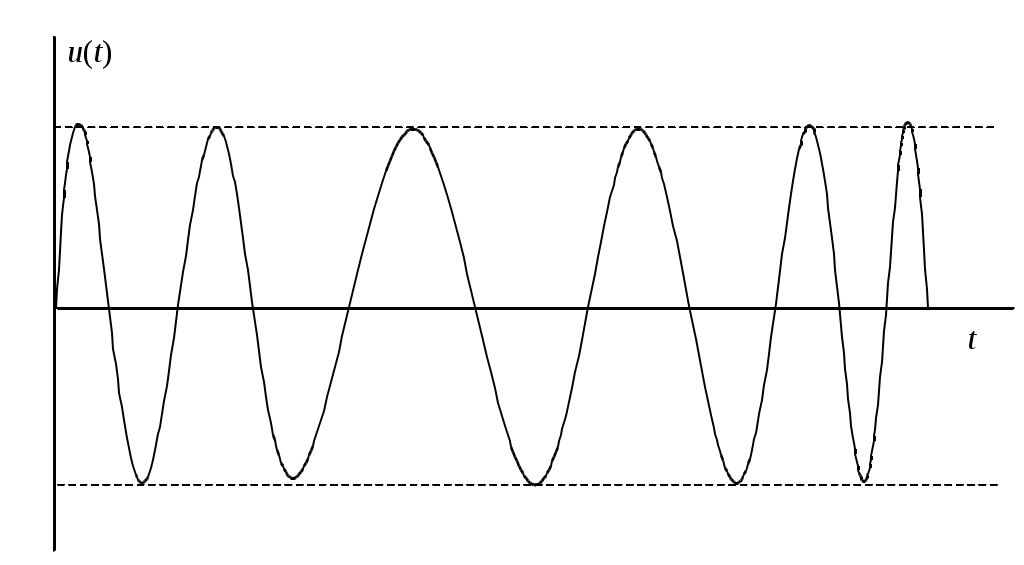
Учитывая соотношение (4), приходим к выводу, что  . Таким образом, гармоническая модуляция фазы с индексом  эквивалентна частотной модуляции с девиацией  .Из приведенного примера видно, что при гармонической угловой модуляции по характеру колебания нельзя заключить, с какой модуляцией имеем дело – с частотной или фазовой. В то же время различие между частотной и фазовой модуляцией проявляется при изменении частоты модуляции. При частотной модуляции величина девиации пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции . При фазовой же модуляции величина пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляции.На рис. 1 показана временная реализация сигнала с угловой модуляцией.
Спектр колебания при гармонической угловой модуляции Рассмотрим несущее колебание с угловой модуляцией вида
В этом выражении опущены для упрощения выкладок начальная фаза и начальная фаза модулирующей функции .Соотношение (11) преобразуется
Используя разложения функций  и  в ряды с использованием функций Бесселя, можно записать [1]
Таким образом, при частотной и фазовой модуляции спектр колебания состоит из бесконечного числа боковых частот, расположенных попарно симметрично относительно несущей частоты 0 и отличающихся от последней на  , где n – любое целое число. Амплитуда n-й боковой составляющей равна  , где – амплитуда немодулированного колебания, m – индекс модуляции.Рассмотрим режим угловой модуляции при малых и больших значениях m. Если  , то имеют место приближенные равенства
При этом выражение (12) переходит в следующее соотношение:
Сравним это колебание с амплитудно-модулированным колебанием, которое для удобства сравнения зададим в аналогичной форме
Из сравнения (14) и (15) видно, что при малых значениях m спектр колебания, как и в случае амплитудной модуляции, состоит из несущей с частотой 0 и двух боковых составляющих с частотами: верхней и нижней . При значениях индекса m от 0,5 до 1 приобретает некоторое значение вторая пара боковых частот, ввиду чего ширина спектра должна быть приравнена 4. Далее, при 1 < m < 2 приходится считаться с третьей и четвертой парами боковых частот и т.д. Спектрограммы для m = 1 и m = 2 представлены на рис. 3 и 4 соответственно.Спектрограмма угловой модуляции для m << 1 показана на рис. 2.
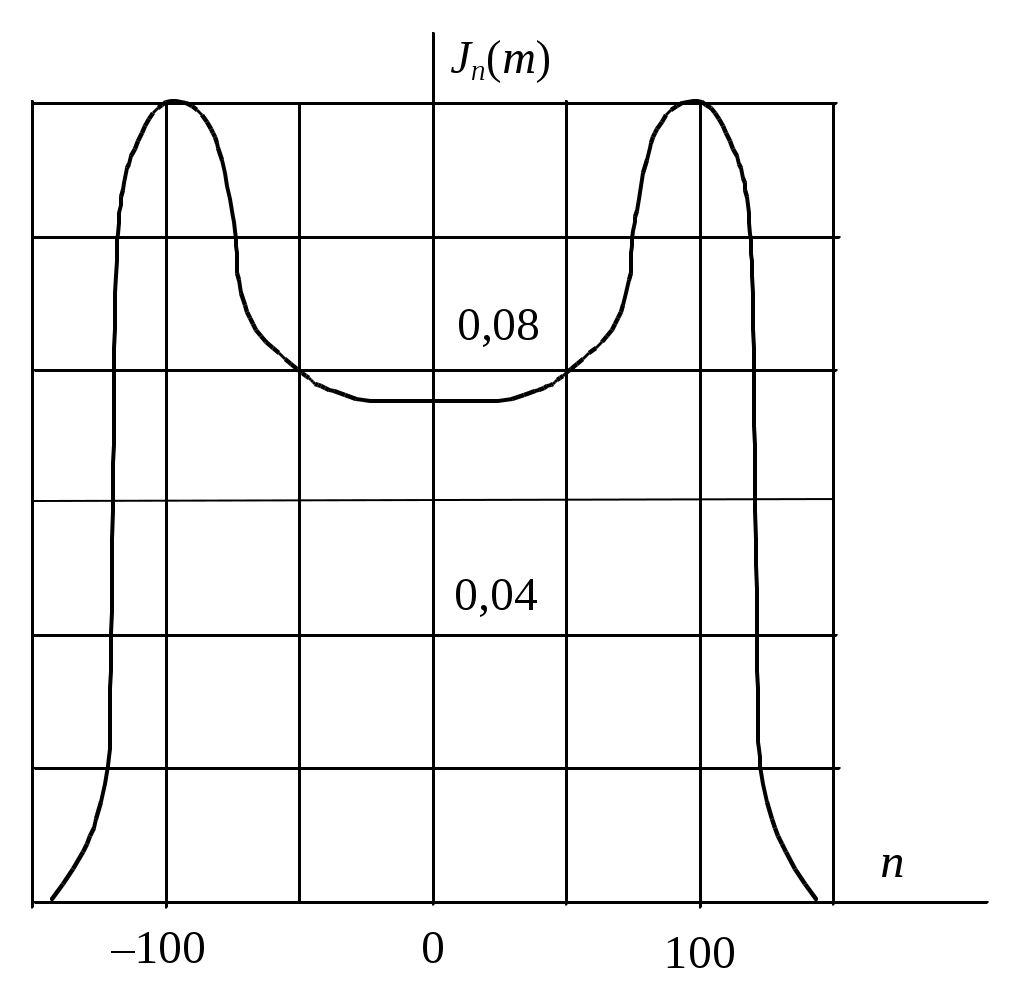
Амплитуды всех составляющих спектра представлены на этих рисунках в виде вертикальных отрезков, длины которых равны  , а расстояние от отрезка  , соответствующего амплитуде колебания несущей частоты, равны n, где – частота модуляции, а n – порядковый номер боковой частоты. Амплитуда результирующего колебания принята за 100%. Обозначенные на рисунках величины , дают амплитуды колебаний соответствующих частот в процентах от амплитуды результирующего колебания.При m >> 1 величина более или менее равномерна при всех значениях n, меньших, чем аргумент m.На рис. 5 показан спектр колебания при m = 100. Из рисунка видно, что наивысший номер n боковой частоты, с амплитудой которой необходимо считаться, приблизительно равен индексу модуляции m (в данном случае n = 100). Приравнивая это максимальное значение  к величине m, приходим к выводу, что полная ширина спектра модулированного колебания
где  . Следовательно, при больших индексах модуляции ширина спектра модулированного колебания близка к удвоенной девиации частоты:
Заметим, что выражение «модуляция с малым индексом» эквивалентно выражению «быстрая модуляция», а «модуляция с большим индексом» эквивалентна «медленной модуляции». Поэтому можно сформулировать следующее положение: при быстрой угловой модуляции (когда << ) ширина спектра модулированного колебания близка к величине 2; при медленной угловой модуляции(когда >> ) ширина спектра близка к величине 2.
2. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ 1. В соответствии с вариантом задания изобразить на экране ПК частотно-модулированное гармоническим сигналом колебание. 2. Для полученной реализации рассчитать и изобразить на экране ПК спектр частотно-модулированного сигнала в области положительных частот. 3. ЗАДАНИЯ
4. СОДЕРЖАНИЕ ОТЧЕТА 1. В отчете необходимо представить основные теоретические положения, связанные с угловой модуляцией. 2. Рассчитать и построить временные реализации и спектральные характеристики модулированных сигналов. 3. Представить результаты моделирования и сравнить их с теоретическими расчетами. 5. КОНТРОЛЬНЫЕ ЗАДАНИЯ 1. Понятие угловой модуляции. 2. Аналитические выражения для частотно- и фазомодулированных сигналов. 3. Временные диаграммы частотно-модулированного сигнала для гармонической модуляции. 4. Спектральная плотность сигналов с угловой модуляцией. 5. Программа моделирования частотно-модулированного сигнала и расчета спектральной плотности. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Сов. радио, 1971. 2. Окунь Е.Л. Радиопередающие устройства. Л.: Судостроение, 1997. ОГЛАВЛЕНИЕ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
,
,
.
.
,
, кГц
,
.
.
,
.
.
.
.
.
.
.
, 
.
,
.