Элементы математической статистики. Корреляционно-регрессионный анализ. (РГЗ). ргз матем. санктпетербургский горный университет Кафедра Высшей Математики Расчетнографическое задание
 Скачать 466.01 Kb. Скачать 466.01 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра Высшей Математики Расчетно-графическое задание Вариант 20 По дисциплине: Высшая математика Тема работы: Элементы математической статистики. Корреляционно-регрессионный анализ Выполнил студент гр. ЭХТ-20-1 Яшагина А. С. (шифр группы) (подпись) (Ф.И.О) Оценка: Дата: 20.12.2021 Проверил: Руководитель работы Доцент Пастухова Е. В. (должность) (подпись) (Ф.И.О) Санкт-Петербург 2021 Задание 1. Для выборок а), б) и в) определить размах R, моду Mo, медиану Me, выборочное среднее 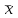 , выборочную дисперсию , выборочную дисперсию 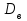 , «исправленную» выборочную дисперсию , «исправленную» выборочную дисперсию 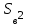 . Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения . Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения 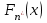 ; для в) построить гистограмму и полигон, эмпирическую функцию распределения ; для в) построить гистограмму и полигон, эмпирическую функцию распределения 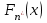 . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| б) | xi | 5 | 7 | 9 | 11 | 13 | 15 | 18 | ||||
| | ni | 10 | 6 | 1 | 7 | 8 | 91 | 2 | ||||
| | | | | | | | ||||||
| в) | xi | [0; 6) | [6; 12) | [12; 18) | [18; 24) | | ||||||
| | ni | 2 | 3 | 4 | 2 | | ||||||
А)
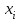 | 1 | 2 | 3 | 4 | 6 | 7 |
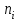 | 1 | 1 | 2 | 3 | 1 | 2 |
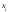 | 1 | 2 | 3 | 4 | 6 | 7 |
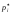 | 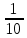 | 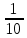 | 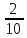 | 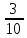 | 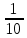 | 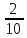 |
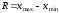 = 7-1=6
= 7-1=6М0 = 4
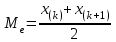 = 3,5
= 3,5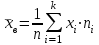 = 1/10*(1*1+1*2+3*2+4*3+6*1+7*2) = 4,1
= 1/10*(1*1+1*2+3*2+4*3+6*1+7*2) = 4,1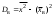 = 20,5 - 4,12=3,69
= 20,5 - 4,12=3,69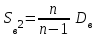 = 10/(10-1)*3,69 = 4,1
= 10/(10-1)*3,69 = 4,1Б)
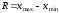 = 18-5=13
= 18-5=13М0 = 15
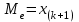 = 11
= 11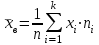 = 1/125*(5*10+7*6+9*1+11*7+13*8+15*91+18*2) = 13,464
= 1/125*(5*10+7*6+9*1+11*7+13*8+15*91+18*2) = 13,464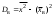 = 191,576-13,4642 = 10,3
= 191,576-13,4642 = 10,3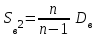 = 125/(125-1)*10,3 = 10,4
= 125/(125-1)*10,3 = 10,4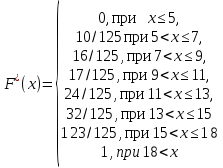
В)
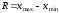 = [6; 18)
= [6; 18)М0 = [12; 18)
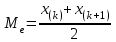 = [9; 15)
= [9; 15)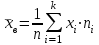 = 1/12*(2*[0; 6) +3*[6; 12) +4*[12; 18) +2*[18; 24)) = [8,5; 14)
= 1/12*(2*[0; 6) +3*[6; 12) +4*[12; 18) +2*[18; 24)) = [8,5; 14)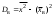 = [121,1; 268,7) - [86,49; 234,09) = [34,61; 34,61)
= [121,1; 268,7) - [86,49; 234,09) = [34,61; 34,61)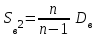 = 11/(11-1)* [34,61; 34,61) = [38,1; 38,1)
= 11/(11-1)* [34,61; 34,61) = [38,1; 38,1)| xi | [0; 6) | [6; 12) | [12; 18) | [18; 24) |
| pi | 2/11 | 3/11 | 4/11 | 2/11 |
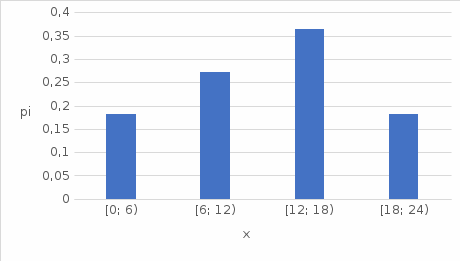
Рис. 1. Гистограмма
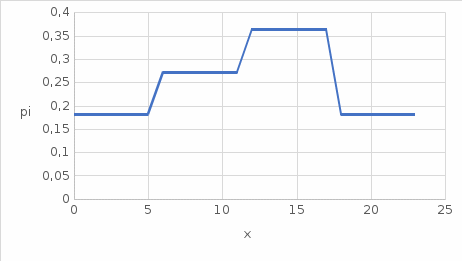
Рис. 2. Полигон частностей
| xi | [0; 6) | [6; 12) | [12; 18) | [18; 24) |
| F(x) | 2/11 | 5/11 | 9/11 | 1 |
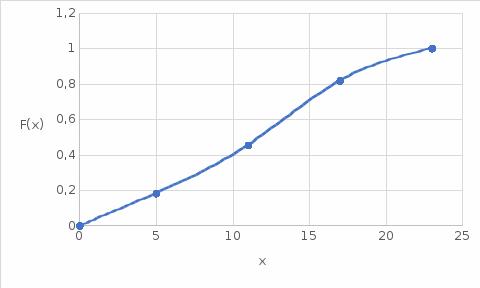
Рис. 3. Эмпирическая функция распределения
Задание 2. Для каждой из приведенных ниже выборок (см. по вариантам) (предполагается, что между признаками существует линейная зависимость):
1. Вычислить выборочный коэффициент линейной корреляции 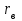 и оценить степень зависимости между переменными;
и оценить степень зависимости между переменными;
2. Найти уравнения прямых линий регрессии Y на X и XнаY, построить их графики;
3. Построить корреляционное поле, линии регрессии;
4. Интерпретировать полученную модель, сделать выводы и прогноз.
В таблице приведена сведения об объеме спроса (у, у.е.) на некоторую продукцию и цены на эту продукцию (х, тыс. руб.).
| хi | 10 | 10,6 | 11 | 12 | 12,5 | 12,8 | 13 | 13,2 | 13,3 | 13,7 |
| уi | 68 | 64 | 59 | 52 | 45 | 42 | 38 | 37 | 35 | 34 |
Получить прогноз объема спроса в случае, если цена на продукцию достигнет 14 тыс. руб.
1. Вычислим выборочный коэффициент регрессии. Для этого составим расчетную таблицу:
 | 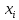 | 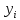 | 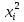 | 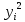 | 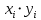 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 10 | 68 | 100 | 4624 | 680 |
| 2 | 10,6 | 64 | 112,36 | 4096 | 678,4 |
| 3 | 11 | 59 | 121 | 3481 | 649 |
| 4 | 12 | 52 | 144 | 2704 | 624 |
| 5 | 12,5 | 45 | 156,25 | 2025 | 562,5 |
| 6 | 12,8 | 42 | 163,84 | 1764 | 537,6 |
| 7 | 13 | 38 | 169 | 1444 | 494 |
| 8 | 13,2 | 37 | 174,24 | 1369 | 488,4 |
| 9 | 13,3 | 35 | 176,89 | 1225 | 465,5 |
| 10 | 13,7 | 34 | 187,69 | 1156 | 465,8 |
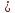 | 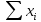 = == 122,1 | 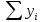 = == 474 | 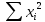 = == 1505,27 | 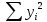 = == 23888 | 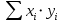 = == 5645,2 |
Коэффициент корреляции рассчитывается по формуле:
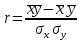 .
.Найдем средние значения:
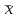 (сумма значений второго столбца, деленная на число строк):
(сумма значений второго столбца, деленная на число строк):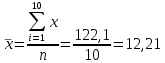 ;
;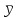 (сумма значений третьего столбца, деленная на число строк):
(сумма значений третьего столбца, деленная на число строк):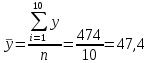 ;
;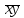 (среднее значение шестого столбца):
(среднее значение шестого столбца):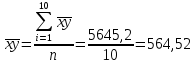 .
.Найдем средние квадратические отклонения
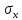 и
и 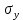 :
: 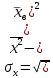 ,
,где
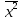 рассчитывается как среднее значение четвертого столбца.
рассчитывается как среднее значение четвертого столбца.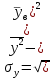 ,
, Где
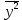 – среднее значение пятого столбца.
– среднее значение пятого столбца.Подставляя найденные значения в формулу коэффициента корреляции, получим:
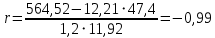 .
.2. Составим уравнения линейной регрессии.
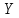 и
и  .
.Для определения параметров
 и
и 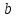 линии регрессии
линии регрессии 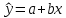 составим систему нормальных уравнений:
составим систему нормальных уравнений: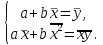
Подставляя найденные в пункте 1 задачи средние значения
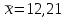 ,
, 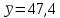 ,
, 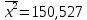 ,
, 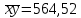 , получим:
, получим: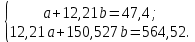
Решая эту систему, найдем
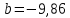 и
и 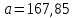 . Тогда уравнение регрессии
. Тогда уравнение регрессии  и
и  имеет вид:
имеет вид: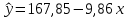 .
.Составим уравнения линейной регрессии
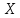 и
и 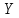 используя формулы:
используя формулы: 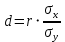 и
и 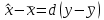 .
.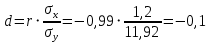
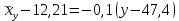 или
или 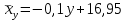 .
.3. Построим корреляционное поле и графики прямых линий регрессии Y на Х и Х на Y (рис. 10). Из чертежа видно, что полученные уравнения хорошо согласуются с исходными данными.
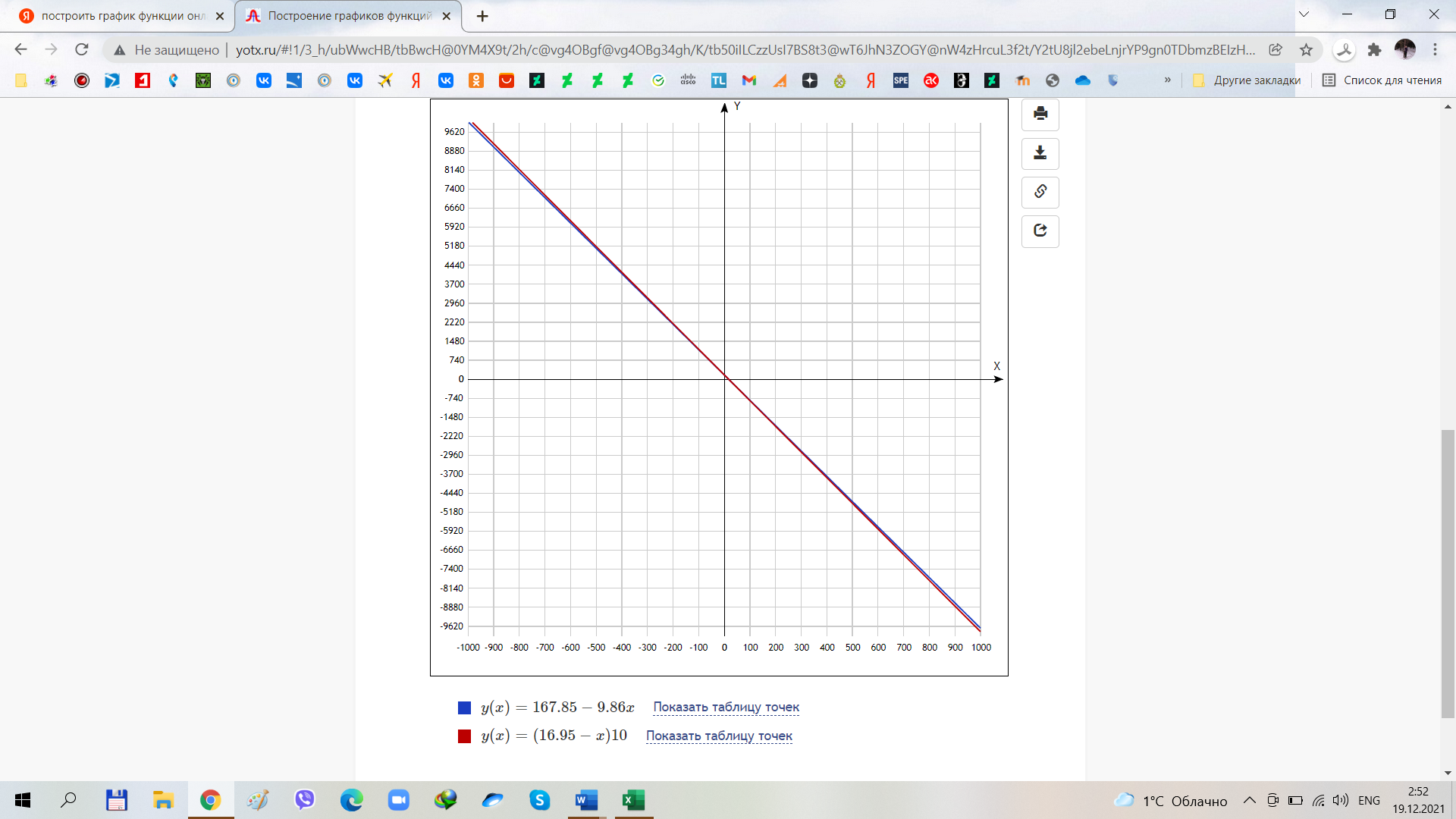
Рис. 4. Корреляционное поле. Линии регрессии
4. По вычисленным коэффициентам, можно сделать вывод, что связь между ценой продукции и объемом спроса обратная и очень тесная, так как полученный коэффициент корреляции (
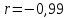 ) отрицательный и очень близок по модулю к единице. Это говорит о том, что чем больше цена продукции (
) отрицательный и очень близок по модулю к единице. Это говорит о том, что чем больше цена продукции (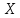 ), тем меньше спрос на нее (
), тем меньше спрос на нее (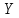 ).
).Выясним, какая часть вариации
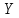 обусловлена вариацией
обусловлена вариацией 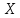 , для этого вычислим коэффициент детерминации:
, для этого вычислим коэффициент детерминации: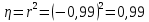 .
.То есть вариация объема спроса на продукцию (
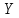 ) на 99% обусловлена вариацией цены на нее (
) на 99% обусловлена вариацией цены на нее (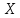 ).
).Отрицательный коэффициент регрессии
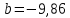 подтверждает то, что связь между ценой продукции и объемом спроса обратная. Вычислим коэффициент эластичности (регрессии):
подтверждает то, что связь между ценой продукции и объемом спроса обратная. Вычислим коэффициент эластичности (регрессии):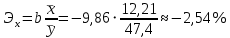 .
.Полученный коэффициент свидетельствует о том, что при увеличении цены продукции на 1%, объем спроса на нее в среднем уменьшается на 2,54%.
Спрогнозируем объем спроса при
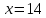 тыс. р. При увеличении цены продукции на 1%, объем спроса в среднем уменьшается на 2,54
тыс. р. При увеличении цены продукции на 1%, объем спроса в среднем уменьшается на 2,54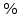 . Подставляя в уравнение регрессии
. Подставляя в уравнение регрессии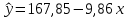 значение
значение 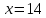 тыс.р., получим
тыс.р., получим 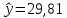 , т.е. при цене продукции
, т.е. при цене продукции 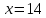 тыс. р. получим объем спроса 29,81 у. е., т.е. на 4,19 у. е. меньше.
тыс. р. получим объем спроса 29,81 у. е., т.е. на 4,19 у. е. меньше.