Сборник. Сборник задач и упражнений по линейной алгебре (1) (1). Сборник задач и упражнений по линейной алгебре

• Название: Сборник задач и упражнений по линейной алгебре
• Анкор: Сборник
• Дата: 22.09.2020
• Размер: 56.8 Kb.
• Имя файла: Сборник задач и упражнений по линейной алгебре (1) (1).docx
• Тип: Сборник задач; #139139

СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО ЛИНЕЙНОЙ АЛГЕБРЕ

УПРАЖНЕНИЯ

1. 
   Вычислить определители второго порядка:
   

7 8 1

1) ; 2)

2 4 3

2 3

; 3)

4  1

4  6

; 4)

5  4

 3 0

_{ 5} ; 5) ₇

2 1 0

; 6) ;

1 0 1

1 1 5

7) ; 8)

0 1 0

9  1

; 9)

4  2

2 0

; 10)

5 2

3 2

; 11)

1 1

 4 1 1

_{ 2} ; 12) _{2 2} ;

7

13)

1

10  1

; 14)

2 3

2 3

; 15)

4 6

5 7

; 16)

0 7

0 29 17

; 17) ;

1 28 18

18)	275 276	175 ; 19) 176	348 248	349 249	; 20)	5731 5732	4731 ; 21) 4732	6826 5826	6827 5827	;
22)	1115 1115	127 ; 23) 128	b b3	4 b2	; 24)	a b a b	a b a b ;

25)

cos  sin 

• 
  sin 
  

; 26)

cos 

; 27) .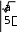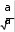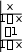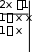

2. 
   Решить уравнения:
   

2 3x

¹⁾ 4  6

 0 ; 2) ^x

2
5
_{x } 4

₁ 1

 2 1

_{ 2} ; 3) _x2

1 _ 6 2 _;

3x 2 1


x² 2 ²

4)

x 1 ¹

 7 _x³

_{ 4} ; 5) _x2

 1 _ ^x

₁  1

_{4 x}3

; 6)

4 ₂

_{ x}² 1  x



;

₁ 9 18


x³ 5 ¹

7)

x² 1 ¹

• x _x⁴

_{ 5} ; 8) _x3

2 _ 2

1 1

• 
  x²
  

.

• x

3. 
   Вычислить определители третьего порядка:
   

4 0

1) 0 9

1 8

3 1

0 ; 2) 2

2 9

0 0 1

3 0 ; 3) 4

8 7 8

2 0 0 1

5 6 ; 4) 4 3

0 7 8 9

2 2

7 ; 5) 4

5 7

0 5

1 3 ;

6 8

1

6) 2

3

1

2  4

6  1 ; 7)

5  8

2 3

1 2  4

2 5  1 ; 8)

3 6  8

9 7 8

1 7  4

1 6  8 ; 9)

2 4  5

2 1 3

1 2 3

2 3 1 ; 10)

3 2 1

1 3 2

3 2 1

6 4 2 ;

7 8 9

2 1 1

11) 4 15

6 9

5 ; 12) 6

7 1

4 5 ; 13)  1 0

2 3 3 1

2 ; 14) 2 6

4 3 9

4 ; 15) 1

6 1

2 1 ;

1 2

0 1

16) 1 0

1 1

1 a

1 ; 17)  1

1. a

2. 
   a  x
   

a 1 ; 18) 0

 1 a x

1 x 1 c

 x  1 ; 19) 1 a

 1  x 1 b

a  b b  c . a  c

4. 
   Найти миноры и алгебраические дополнения элементов первой стро- ки и первого столбца следующих матриц:
   

_ 4  5 7 _

 

_ 0 2 1 _

 

_ 1 2 3_

 

_ 9 3 1 _

 


1) _ 8  3 2_; 2) _ 3 5 4_; 3) _ 3 6

9 _ ; 4) _ 4 5 7 _ .

1

9

7

8





6

 6
   
 

  

4

7

8

6

5

2
   

5. 
   Вычислить определители, разложив их:
   

2. 
   

   1	1	1
   1) 2	2	1	– по элементам первой строки;
   1	2	2
   1	3	5

   
   
   
   

   2	4	6
   8	9	7
   1	1		2
   2	1		1

   
   
   
   – по элементам третьей строки;
   

2. 
   – по элементам второго столбца;
   

			1	 2
			2	1	2
	4)		1	2	2
			2	2	1
				2 1
5)		1 0 5 0

2

– по элементам третьего столбца;

1

3 – по элементам второго столбца;

1

 2

6) 1

5

1 3

 2 4

0  2
– по элементам третьей строки;

8

7) 0

3

1

0  2

 1 4

2  9

2 3
– по элементам первого столбца;

8) 3 1

2 3

^a11

2

1

^a12

– по элементам второй строки;

^a13

9) 1 2

 1 0

3 – по элементам первой строки.

0

6. 
   Вычислить определители, предварительно преобразовав их:
   

1 a

1) 0 a a

1

0

0a

9

; 2) 6

1

7 8 1

4 5 ; 3) 2

2 3 1

4 3 3 2 1

 5 1 ; 4) 6 5 4 ;

 3 2 9 8 7

58

5) 69

77

63 59 46

73 71 ; 6) 57

81 79 68

40 30

54 55 ; 7)

65 66

251

363

574

125

181

288

126

182 .

289

7. 
   Проверить справедливость следующих равенств:
   

2

1) 3

1

2 3 2

1 2  3

3 1 1

1 2 1

2 1 ; 2) 4

3 3 6

 2 2 1

 1 15  4

 8 9 6

 2 3

 1 5 .

 8 7

8. 
   Вычислить определители четвертого порядка:
   

1 1 1

₁₎ 2 1 8

₁ 1 2

3 2	1	3		1	3	2	1		3	3	1	2
4 2	4	0		1	8	1	4		4	0	4	1

^{ 2} ; 2) ^{1 1}

^{3 0} 2 2 8 3

^{2 2} 1 1 1 1

; 3) ;

1	1	1		 1			6	3		4	5				3		6		5			4
1	 1	 1		1	; 9)		2	2		2	3		; 10)		1		2		3			3	.
1	2  3			1	3			3		3	2		3			3			2		2
2	1 4			5	2			2		3	3		2			1			1		1

1	2	3	4		4	3	2	 1		1	2	4	3		4	3	4	5
1	1	2	2	; 5)	8	6	4	 2	; 6)	5	1	1	2	; 7)	3	1	2	3
1 2 3 0 1 3 2 1					1 0 3 5 9 7 6 5					7 5 9 8 6 7 8 9					2 3 1 2 1 2 3 1

4) ;

8)

9. 
   Вычислить определители пятого порядка:
   

1 2 1

0 1 0

¹⁾ 2 3 1

0 2 0

1 1 2

1 1 ^{2 8 7 6 5}

 2 3 ^{3 0 4 1 2}

 4 1 ^{; 2) 1 3 2 1 1 .}

 3 2 4 2 3 0 1

1 4 3 8 7 6 5

0

10. 
    При каком k определитель 2
    

k

 3 0

0  2

4 2

равен нул