Сборник задач по практикам. Сборник задач по гидравлике может использоваться в качестве учебного пособия для практических занятий по курсу гидравлики и являться дополнением к лекционному курсу

• Название: Сборник задач по гидравлике может использоваться в качестве учебного пособия для практических занятий по курсу гидравлики и являться дополнением к лекционному курсу
• Анкор: Сборник задач по практикам.doc
• Дата: 27.08.2018
• Размер: 1.79 Mb.
• Имя файла: Сборник задач по практикам.doc
• Тип: Сборник задач; #23634
• страница: 11 из 12

9 СОПРЯЖЕНИЕ БЬЕФОВ

Задача 9.1. Определить глубину в сжатом сечении струи, переливающейся через водослив практического профиля (m = 0,49,  = 0,95). Высота водослива Р = 7 м (рис. 25), расход на 1 пог. м пролета q = 8 м³/с/м. Выяснить форму сопряжения потока в ниж­нем бьефе, если бытовая глубина h_б = 3 м.

Решение. Определим напор над гребнем водослива с учетом скорости подхода из формулы расхода незатопленного водослива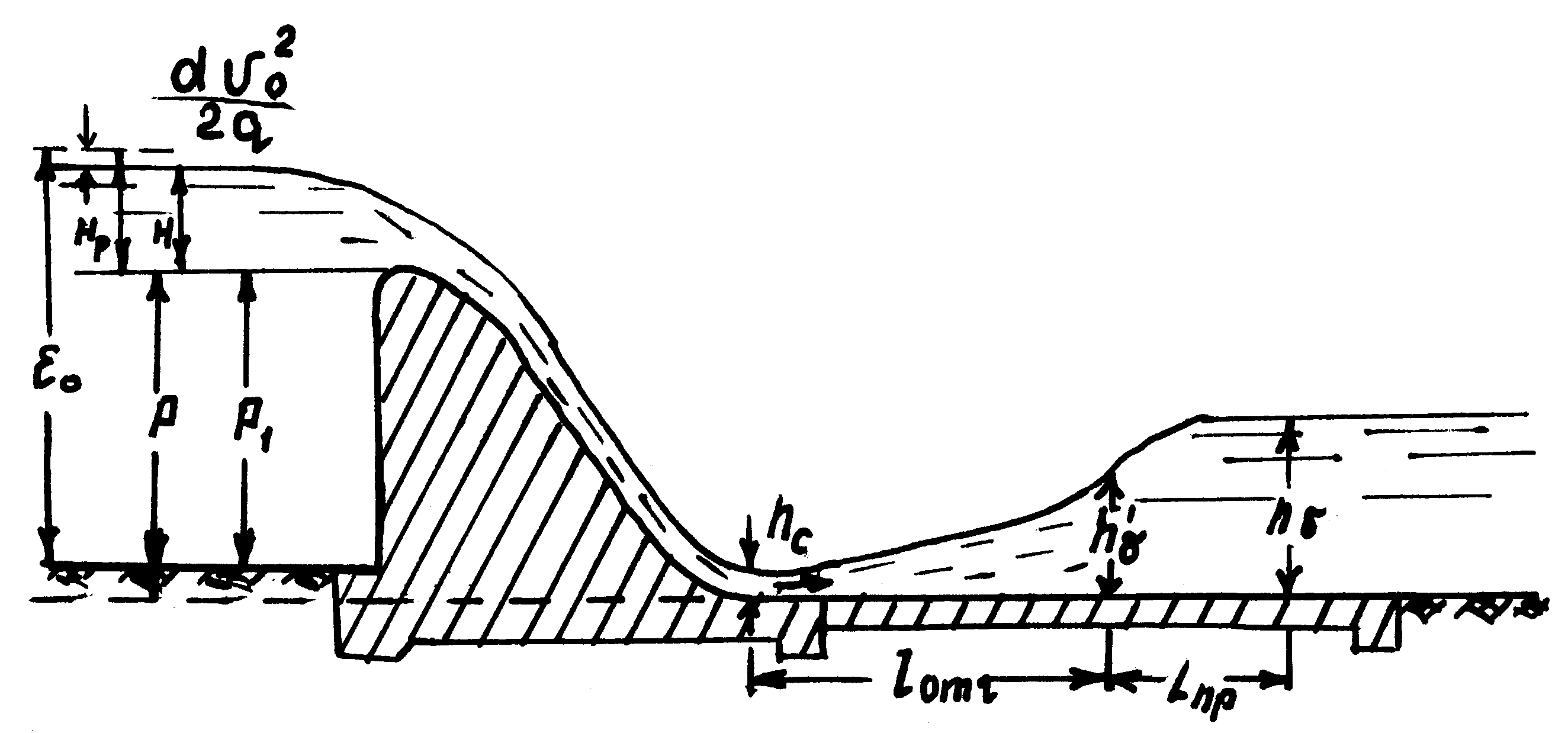

м.



Рисунок 25

Удельная энергия в верхнем бьефе относительно дна нижнего бьефа Е₀ = Р + Н₀ = 7 + 2,39 = 9,39 м.

Определение глубины в сжатом сечении и сопряженной с ней проведем двумя способами.

1-й способ. Вычислим Ф (_с)



где q – расход на 1 пог. м пролета плотины;

b – ширина сливного фронта или длина гребня;

Е₀ – удельная энергия в верхнем бьефе относительно дна нижнего бьефа;

 – коэффициент скорости, зависящий от типа плотины.

По таблице XXIX [1] такому значению Ф (_с) соответствуют _с = 0,069 и _с" = 0,448.

Глубина в сжатом сечении h_c = _сЕ₀ = 0,0699,39 = 0,646 = 0,65 м. Вторая сопряженная глубина h"_c = 0,4489,39 = 4,20 м. Так как h"_c = 4,20 больше h_б = 3 м, то сопряжение произойдет с отогнанным прыжком.

2-й способ. Найдем h_c по формуле (113).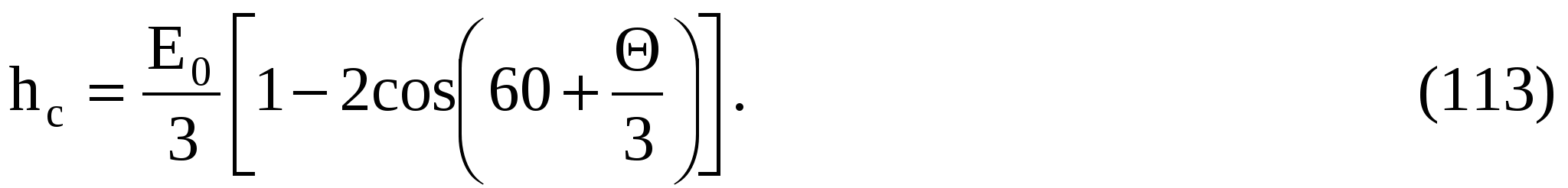



В этой формуле значение угла определяется по формуле





Этому значению соответствует угол =1950’ .

По формуле 113 определяем глубину в сжатом сечении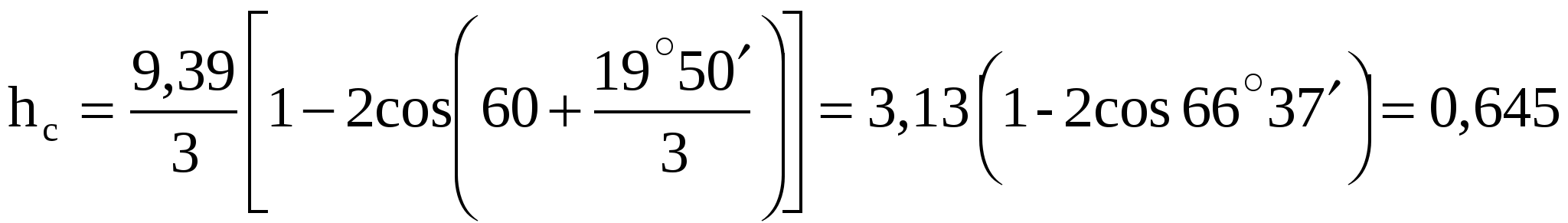

м.

Вторая сопряженная глубина при =1,0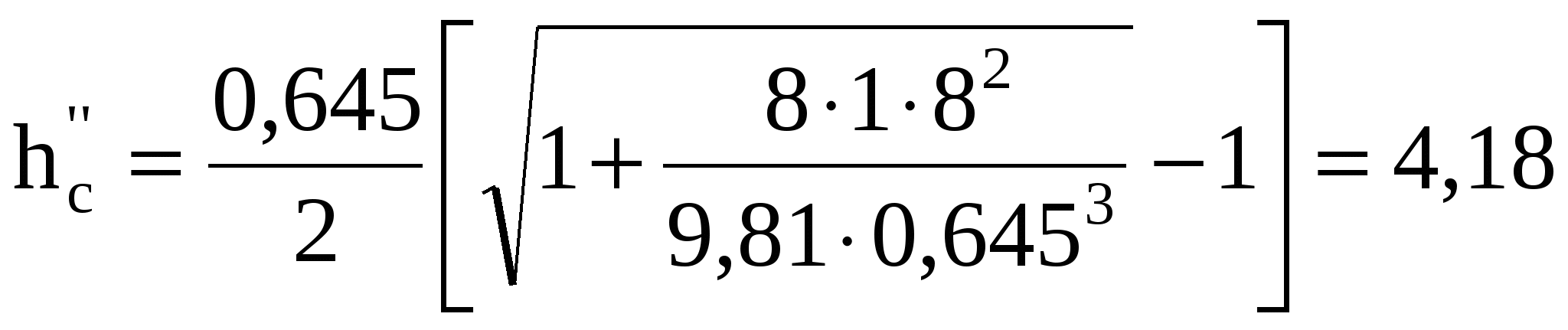



м,

что практически совпадает с найденным выше значением.

Задача 9.2. Рассчитать глубину водобойного колодца прямо­угольного сечения для сооружения, показанного на рисунке 26, пренебрегая перепадом при выходе потока из водобойного колодца. Рас­ход Q = 12 м³/с, ширина b = 4 м, Н₀ = 1,8 м, высота порога Р = 2 м. Бытовая глубина в канале h_б = 1,6 м.

Решение. Выясним характер сопряжения потока с нижним бьефом, для чего найдем Ф (_с) при 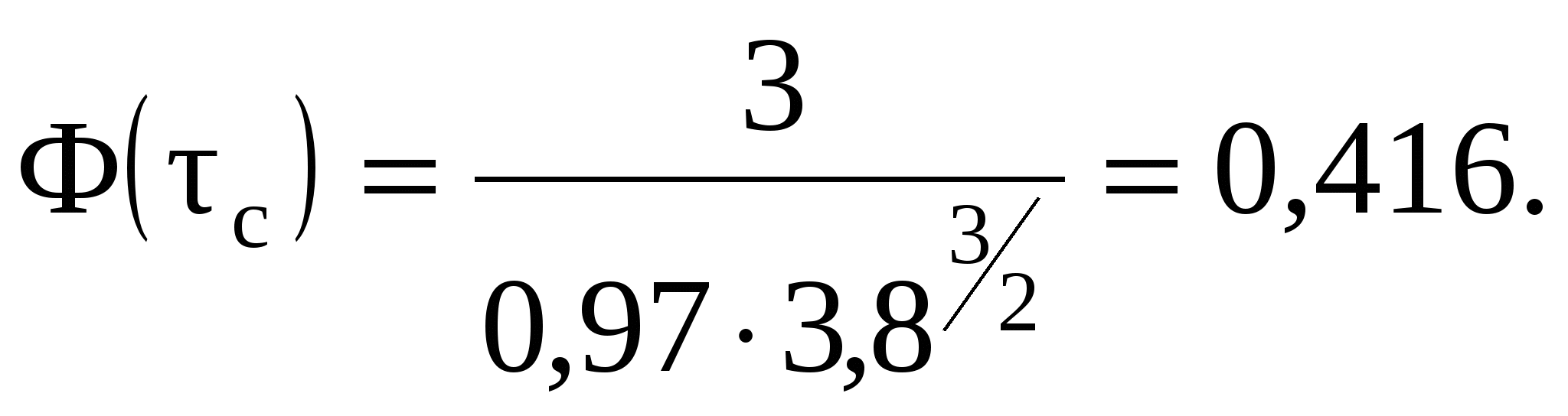м³/с/м и Е₀ = Р + Н₀ = 2 + 1,8 = = 3,8 м.



По таблице XXIX [1] _с = 0,099 и h_с = 0,0993,8  0,38 м.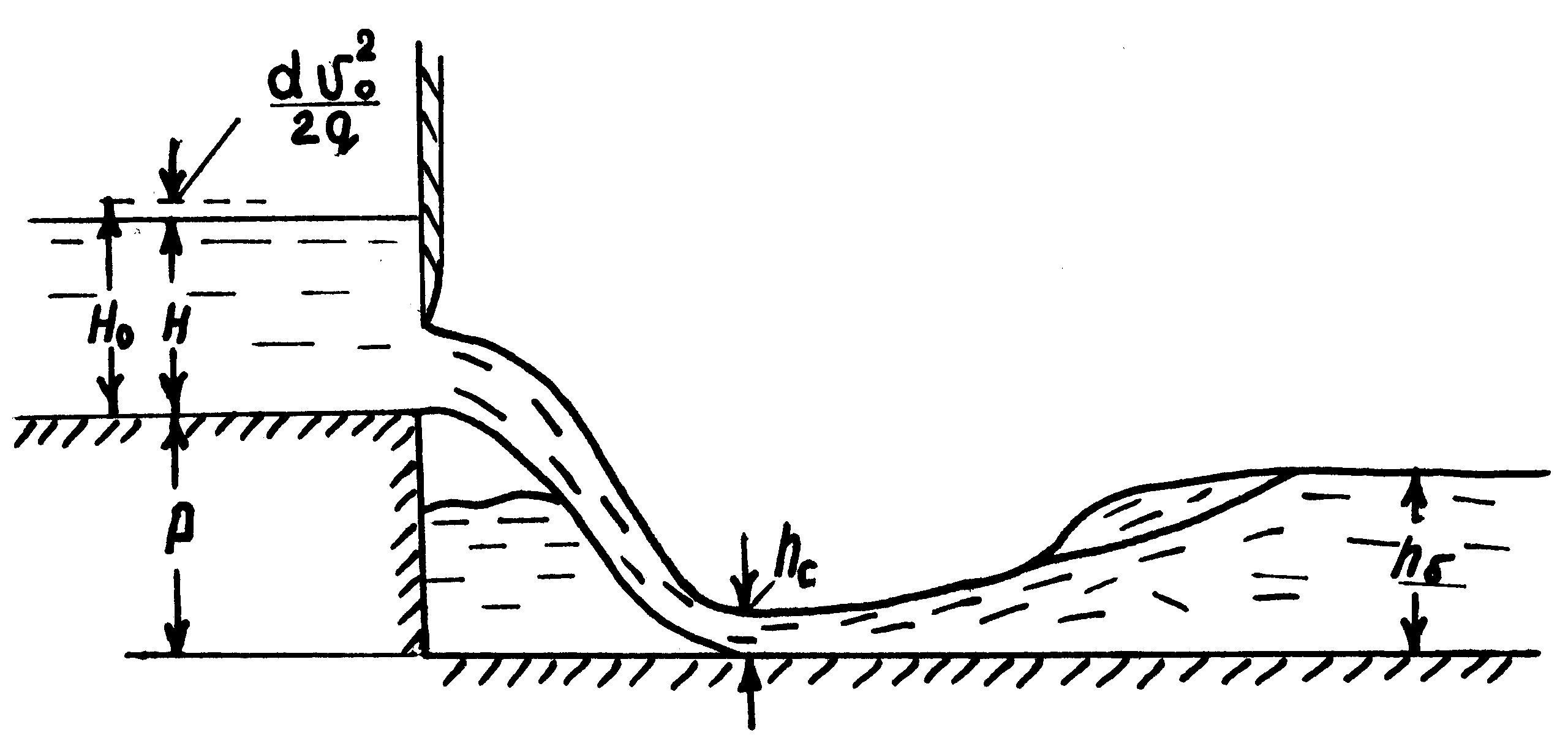


Рисунок 26

Вторая сопряженная глубина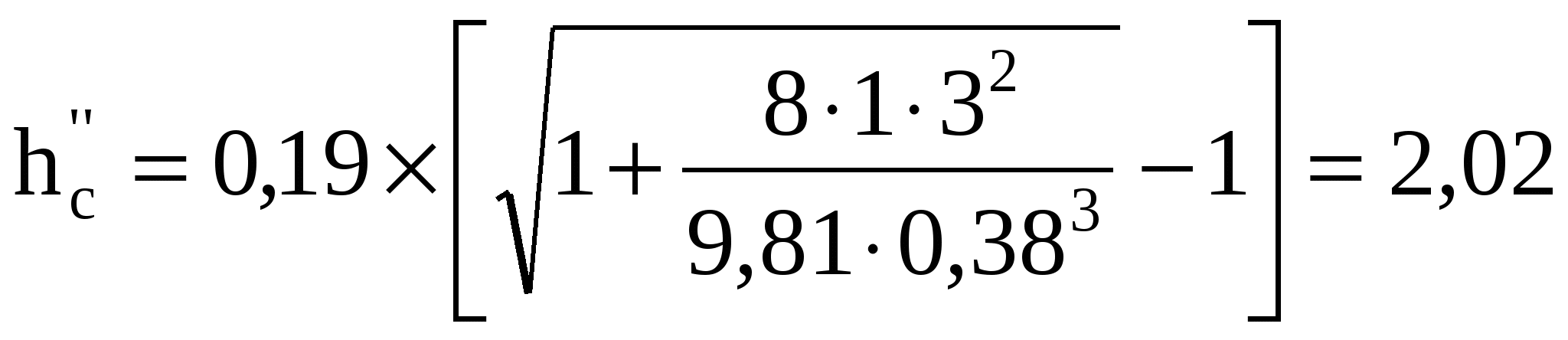

м.

Так как h"_c > h_б, то проектируем водобойный колодец. Глу­бина колодца в первом приближении равна d = h"_c – h_б = 2,02  0,5 м.

При устройстве колодца удельная энергия увеличится

Е^′₀ = Р + Н₀ + d = 3,8 + 0,5 = 4,3 м.

Определим глубину в сжатом сечении при устройстве колодца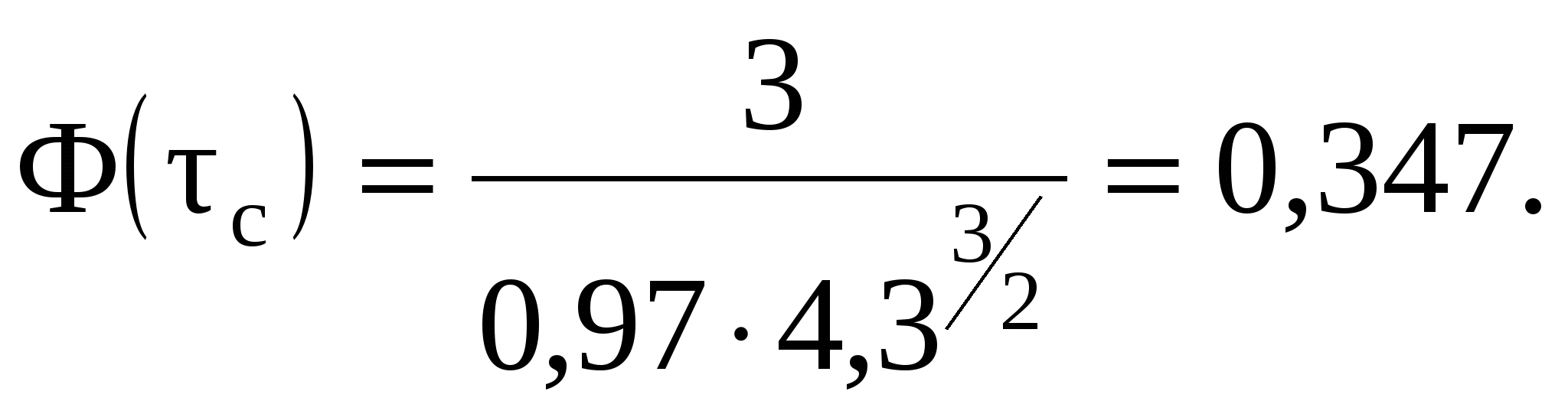



Этому значению Ф (_с) соответствует _с = 0,082, тогда, h_c = 0,0824,3 = = 0,352  0,35 м;

Вторая сопряженная глубина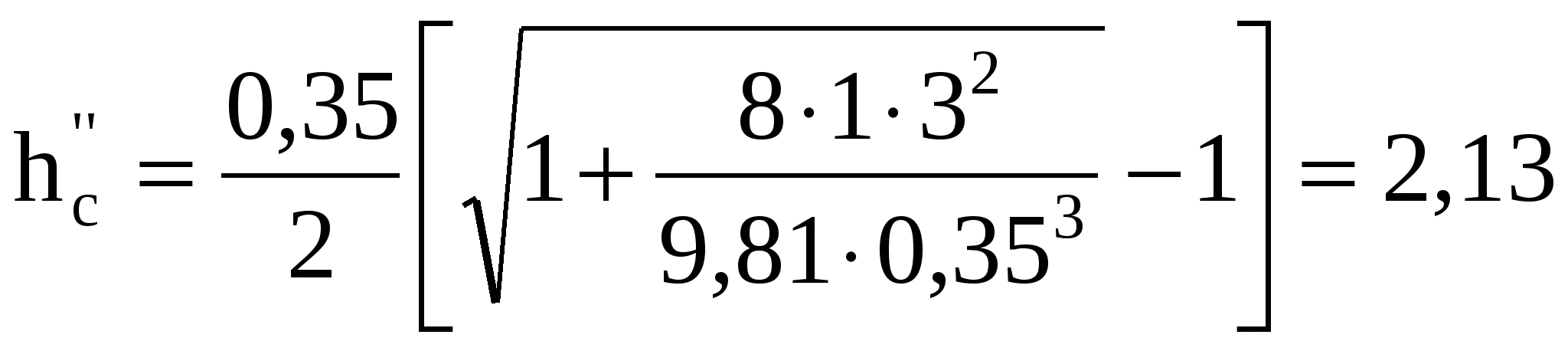

м.

Глубина колодца d = h"_c – h_б = 2,13 – 1,6 = 0,53 м (расхождение  6 %).

Зададимся значением d = 0,53 м и, проделав расчет аналогично вышеописанному, получим: h_c = 0,35 м, h"_c = 2,13 м и d = 0,53 м.

Окончательно принимаем d = 0,55 м. Проведем расчет, используя вспомогательный график А. А. Угинчуса (рисунок 1, приложение В).

Определим критическую глубину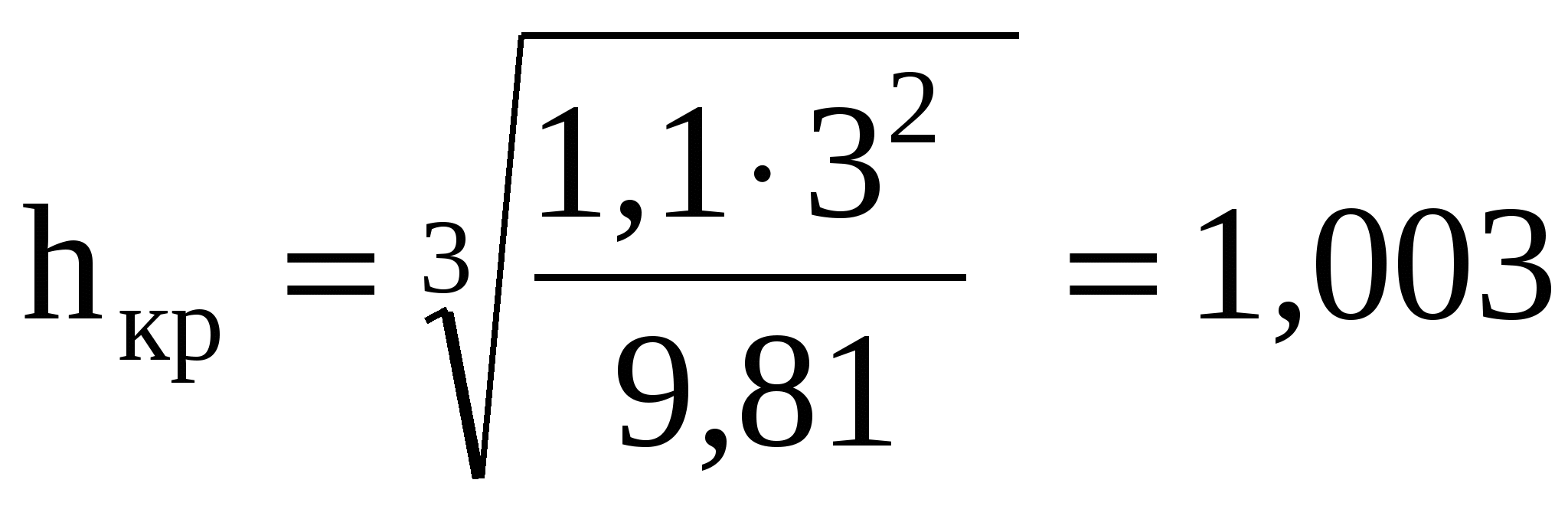



1м.

Вычислим z₀ = Р + Н₀ – h_б = 3,8 – 1,6 = 2,2 м.

По рисунку 1 приложение В при  = 0,97 и 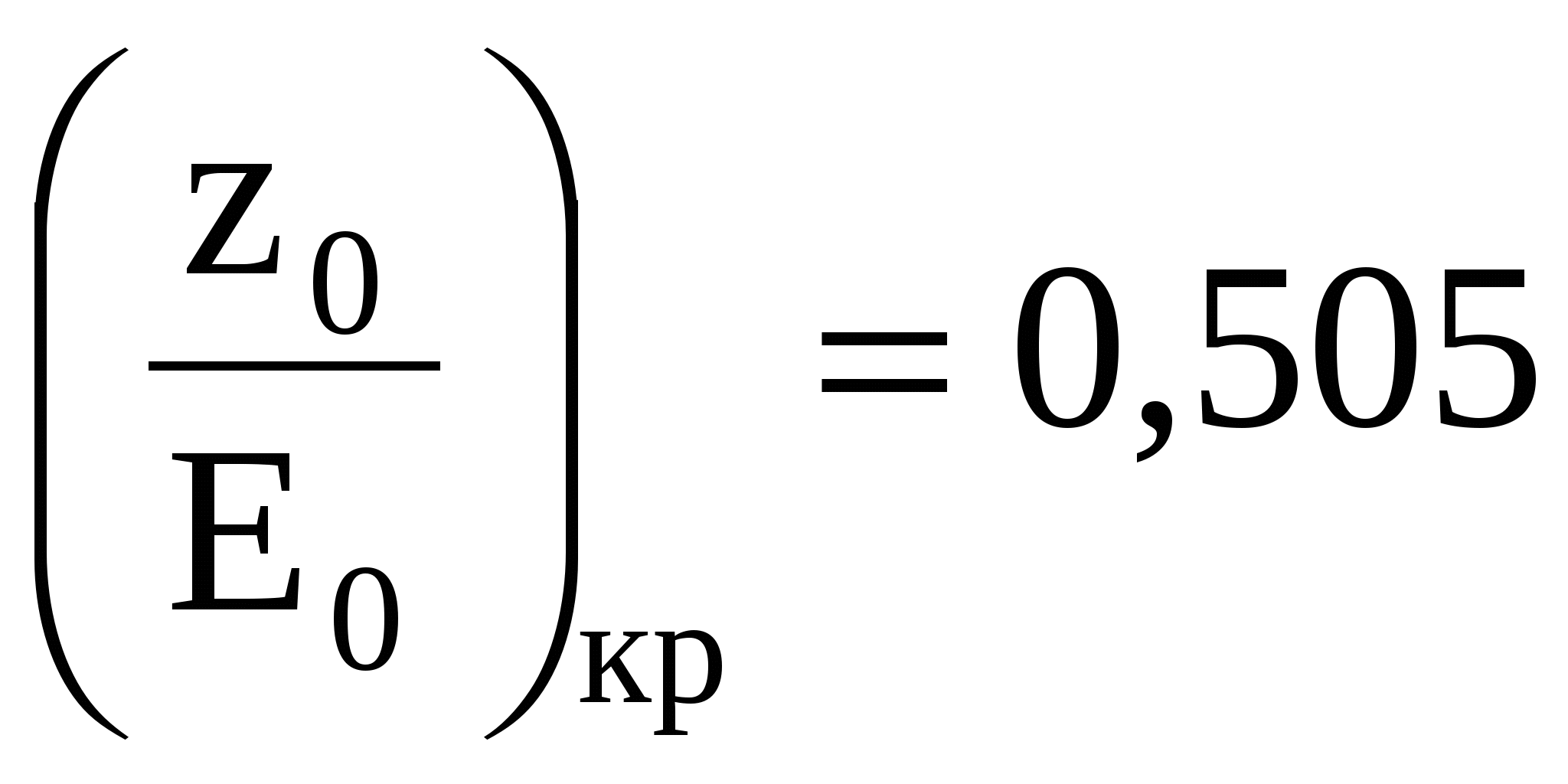находим

.

Глубина колодца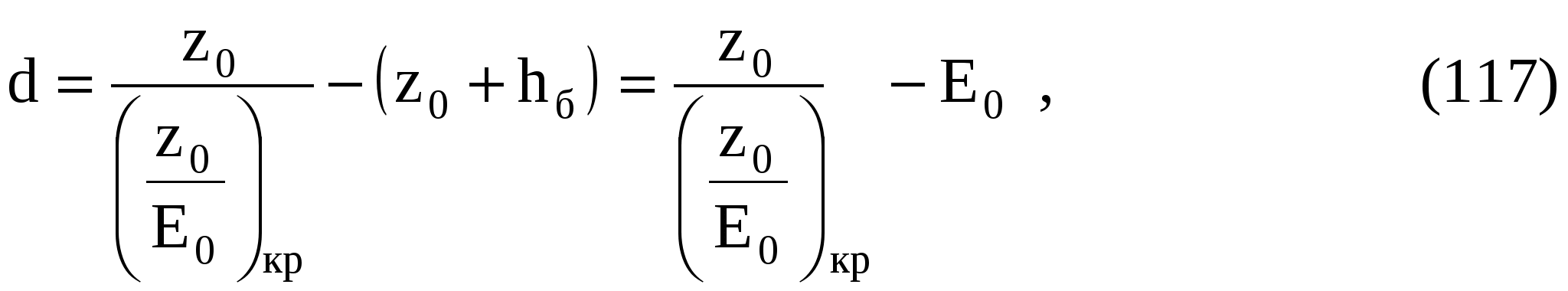





что практически равно найденному выше значению.

Задача 9.3. Рассчитать комбинированный водобойный колодец у плотины (рис. 27) при следующих данных: q = 8 м³/c/м; высота плотины Р = 7м; Н₀ = 3 м; глубина в нижнем бьефе h_б = 3 м, коэф­фициент скорости для плотины ₁ = 0,95; для водобойной стенки ₁ = 0,90. Расчет высоты водобойной стенки выполнить так, чтобы сопряжение переливающейся через стенку струи с потоком нижнего бьефа происходило в форме прыжка в сжатом сечении.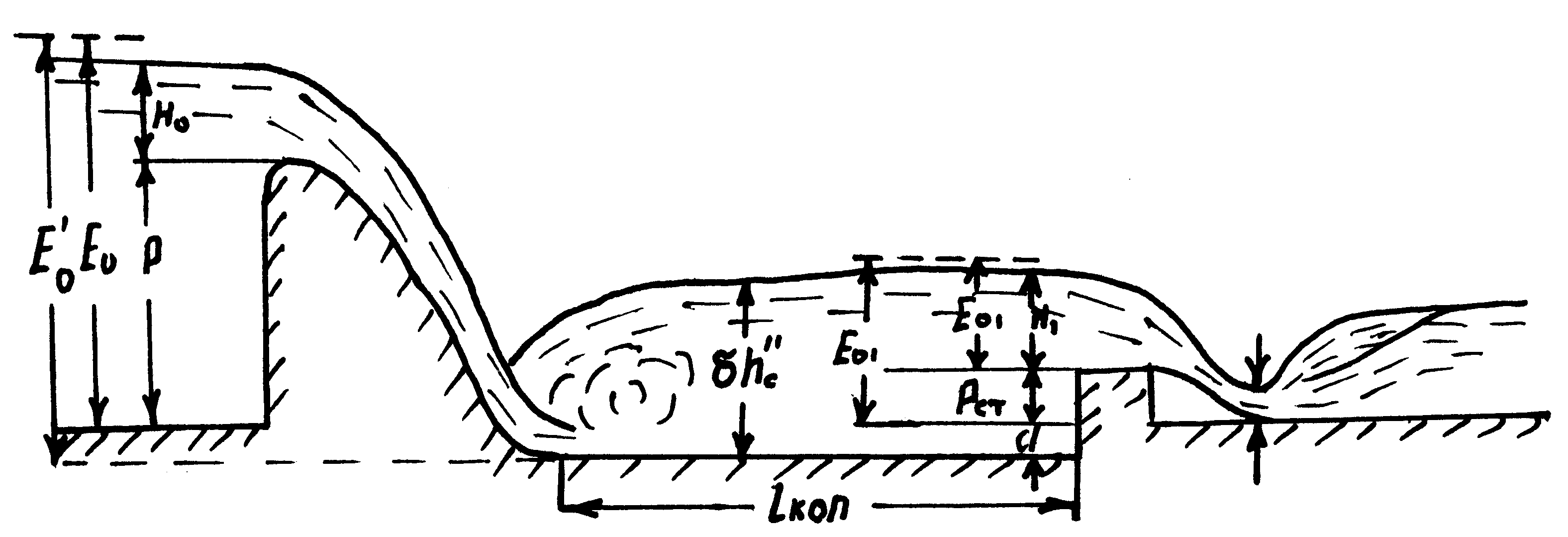



Рисунок 27

Решение. Выясним форму сопряжения при Е₀ = Р + Н₀ = 7 + 3 = 10 м.

Вычисляем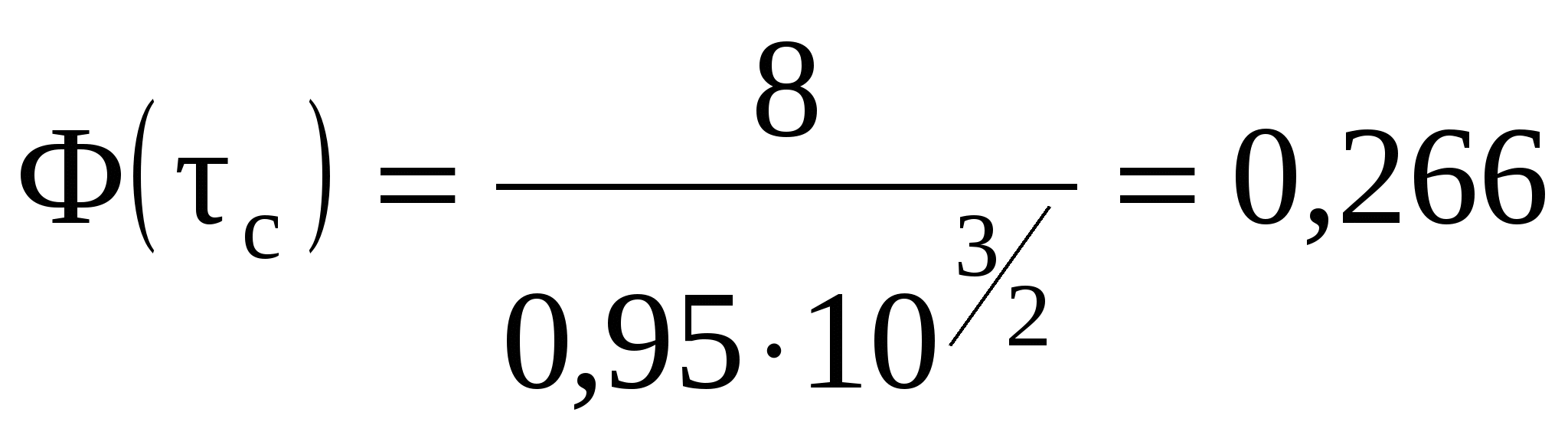





и по таблице XXIX [1] находим "_с = 0,428 при ₁ = 0,95 и _с = 0,062. Глубина в сжатом сечении h_с = _сЕ₀ = 0,06210 = 0,62 м. Вто­рая сопряженная глубина h"_с = "_сЕ₀0,42810 = 4,28 м.

Так как h"_c > h_б = 3 м, то сопряжение произойдет в форме отогнанного прыжка.

Запроектируем комбинированный колодец. Высоту водобойной стенки найдем из условия, чтобы за ней образовался прыжок в сжатом сечении. Определим вид прыжка за водобойной стенкой





Так как П_кб = 0,242 < 0,375, то сопряжение произойдет в фор­ме совершенного прыжка.

Найдем первую сопряженную глубину для бытовой глубины по формуле совершенного прыжка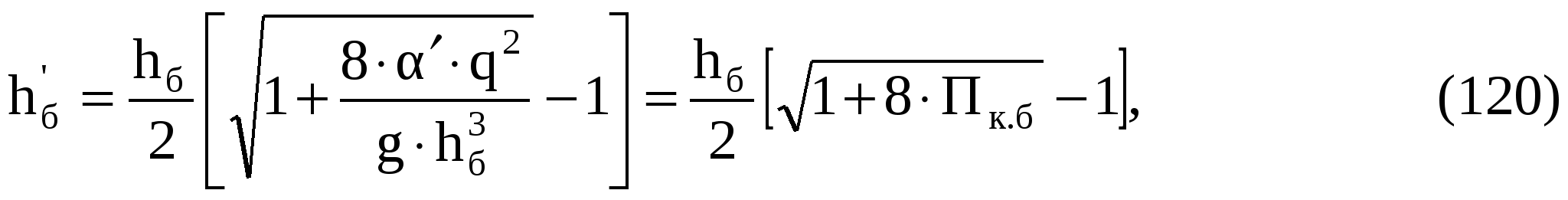





Эта глубина будет равна глубине за водобойной стенкой в сжа­том сечении.

Определим удельную энергию перед стенкой относительно дна нижнего бьефа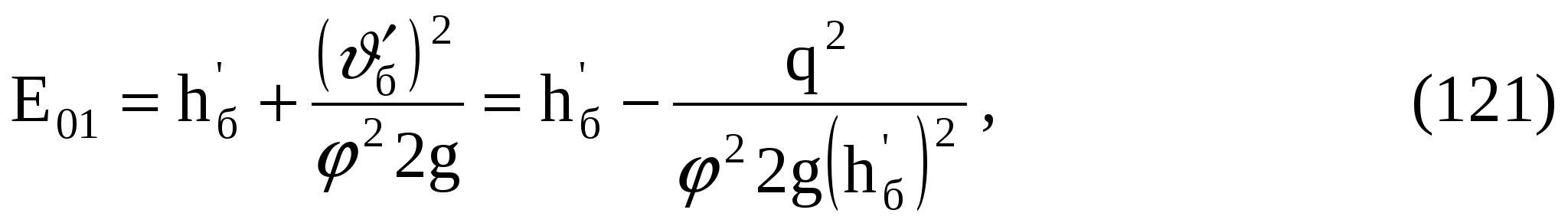





Напор над стенкой с учетом скорости подхода (при m = 0,42)



м.

Высота стенки, при которой произойдет сопряжение с прыжком в сжатом сечении м. Если стенку принять меньшей высоты, чем 1,95 м, то сопряжение произойдет с надвинутым прыжком, если большей, то с отогнан­ным прыжком.

Примем Р_ст = 1,95 м.

Глубина колодца в первом приближении равна



где м.

Напор над стенкой при



м/c,



м.

В первом приближении d = 4,5 – (1,95 + 2,46) = 0,09  0,1 м.

Вычислим удельную энергию Е^’₀ = Р + Н₀ + d = 10,1 м и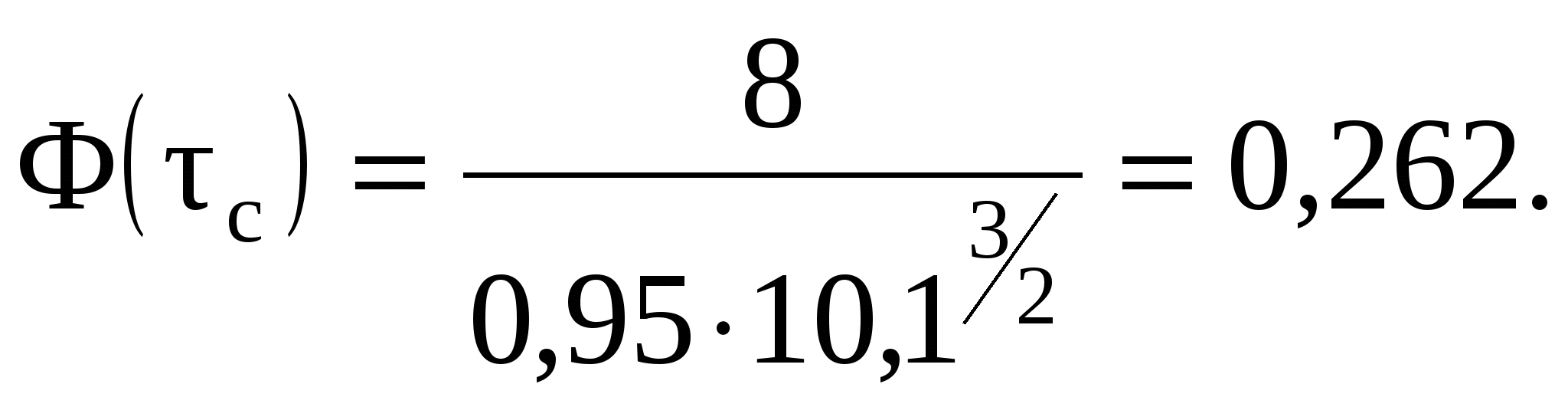



По таблице XXIX [1] "_с = 4,25 '_с = 0,061.

Глубина в сжатом сечении при устройстве колодца h'_с = 0,06110,1 = = 0,616м, т. е. глубина в сжатом сечении уменьшилась, а вторая сопряжен­ная возросла h"_с = 0,42510,1 = 4,3 м. Скорость подхода м/c. Напор над стенкой м. Глубина водобойного колодца d = 4,51–(1,95+2,46) = 0,10 м, что совпадает с тем значением, которым мы задались в первом приближении. Длина колодца l_кол = 3h"_с = 34,3 = 12,9  13 м.

Так как высота стенки получилась очень большой по сравне­нию с глубиной колодца, то желательно уменьшить высоту стенки и увеличить глубину колодца.