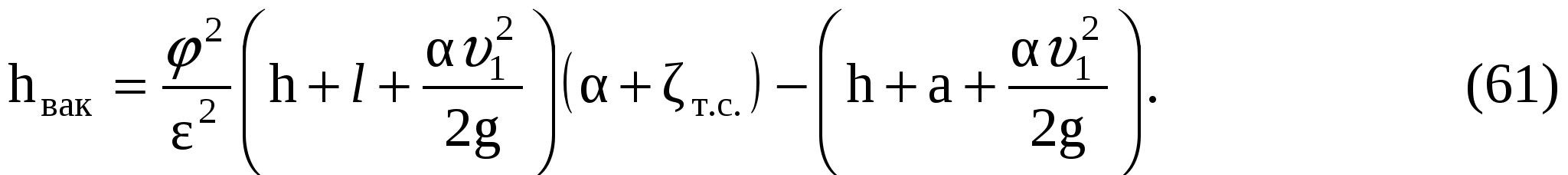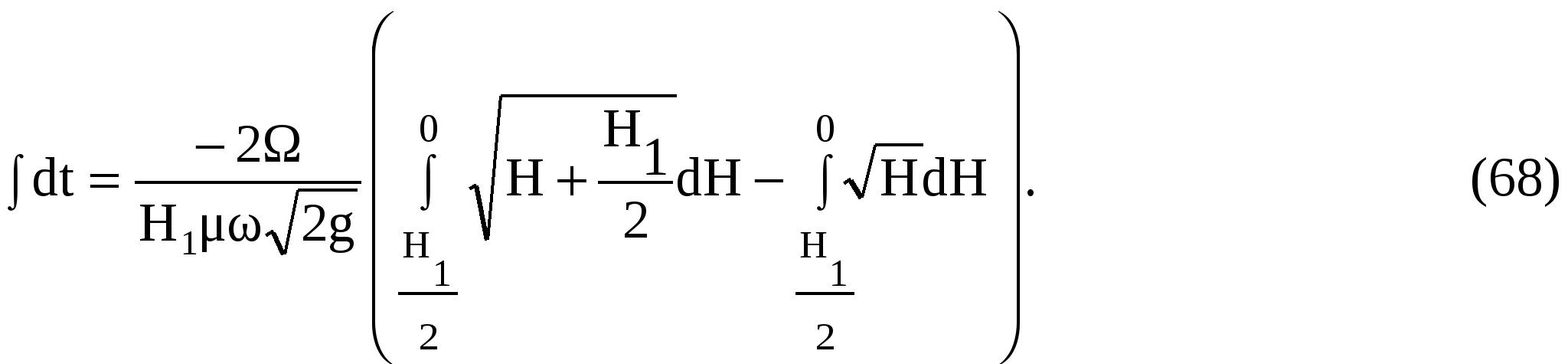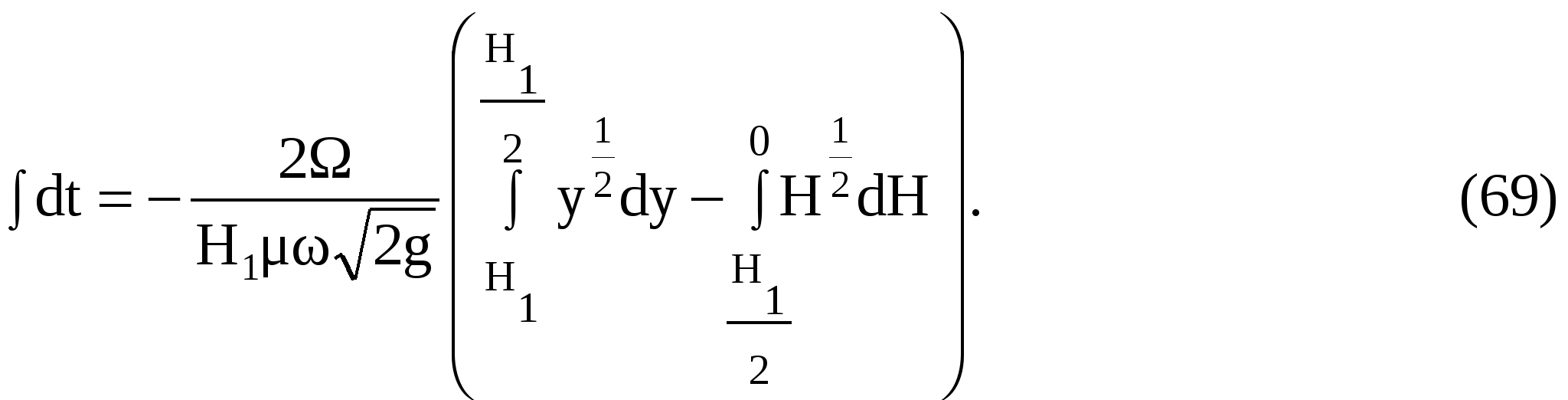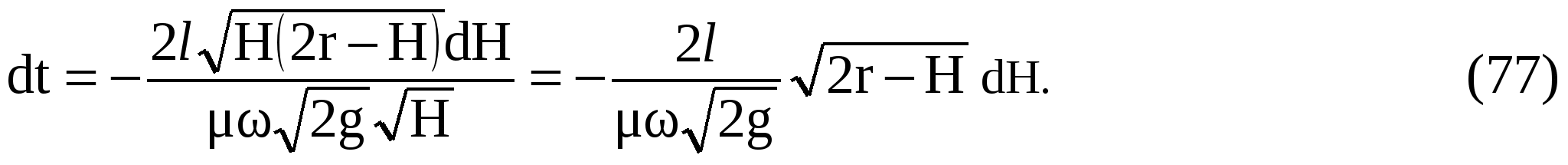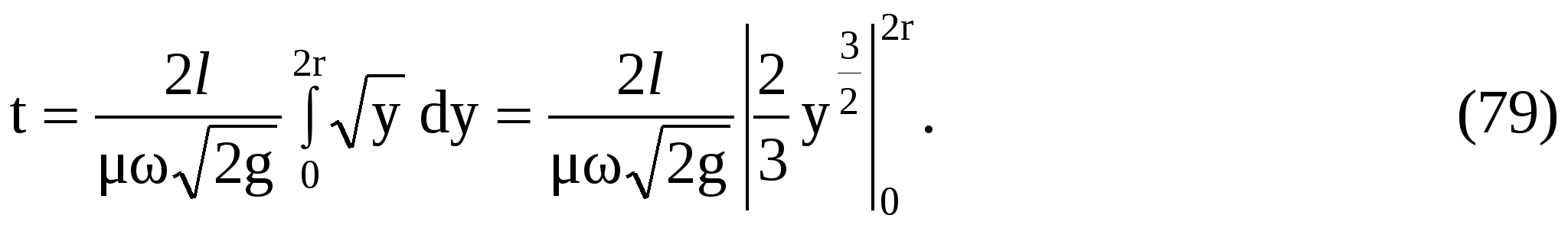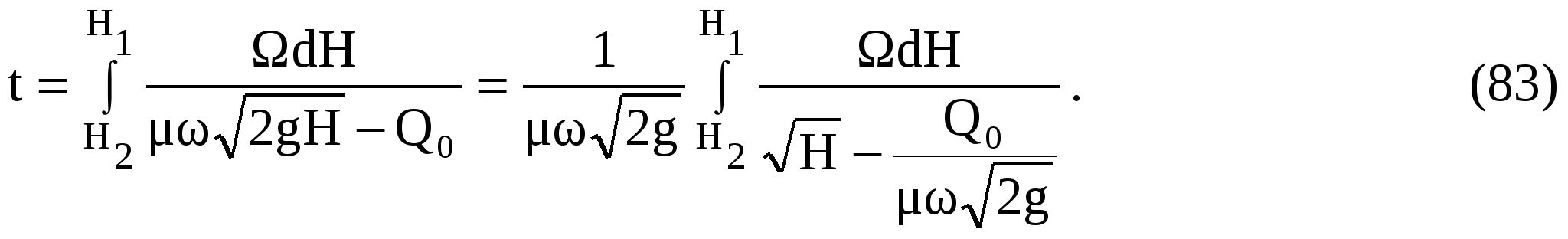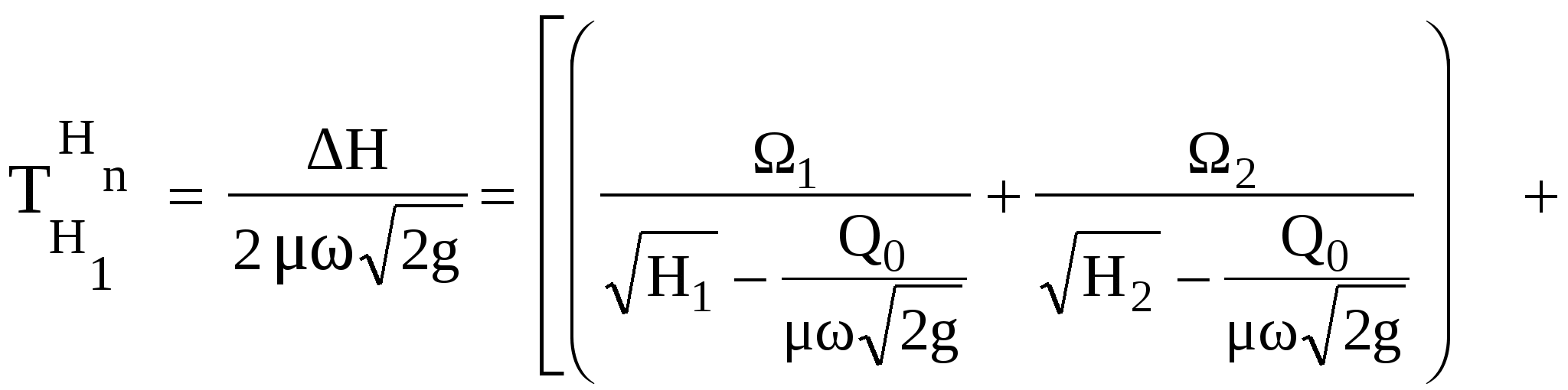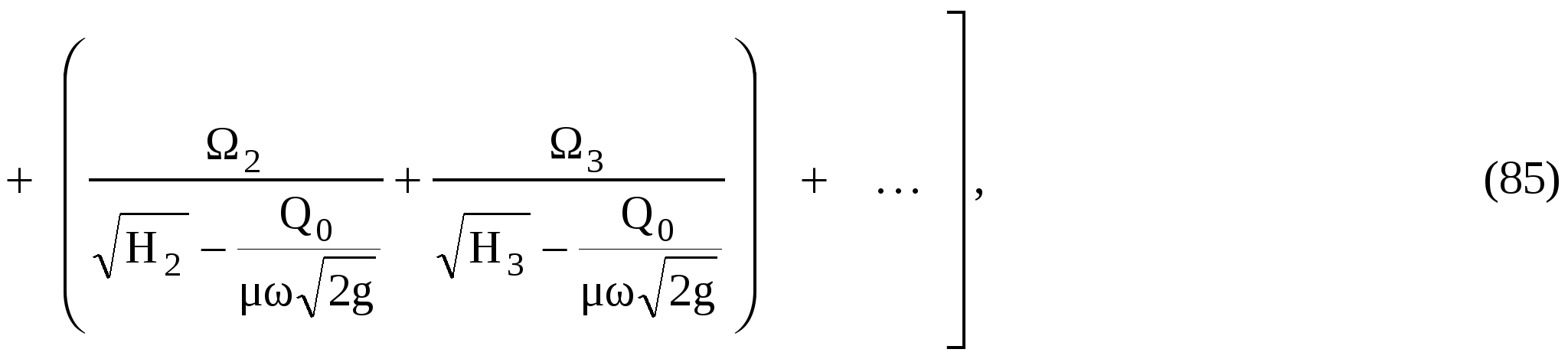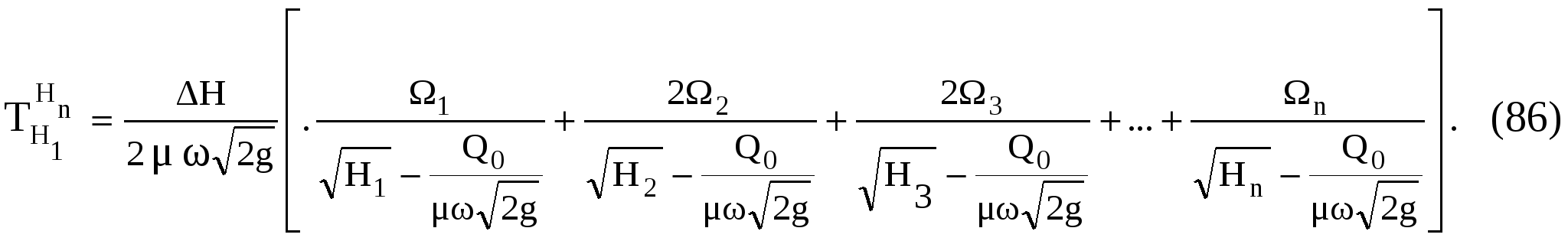Задача 3.1. Через цилиндрический насадок, расположенный в стенке, расходуется вода в количестве Q = 0,0056 м3/с. Диаметр насадка d = 0,038 м, длина l = 0,15 м. Определить напор Н над центром насадка, скорость с и давление pcв наcадке (в сжатом сечении).
Решение. Длина насадка l = 0,15 м 43,8, следовательно, можно принять коэффициент расхода = 0,82. При d = 0,038 м. площадь = 0,00113 м2. Напор над центром насадка определяется по формуле


Скорость в выходном сечении насадка
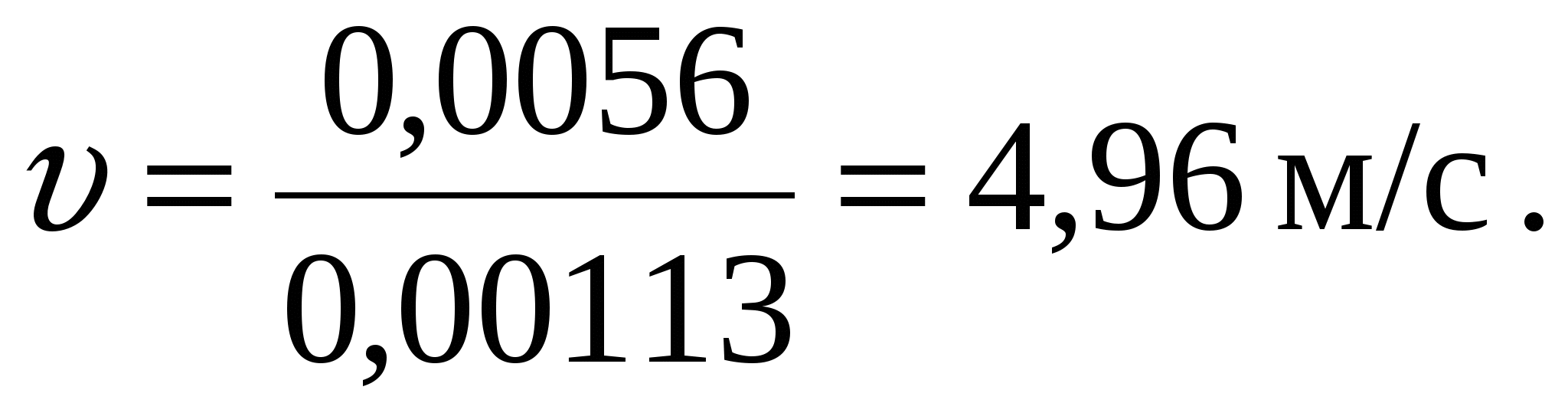
Из условия неразрывности сс = определим скорость в сжатом сечении, полагая = с/=0,64,

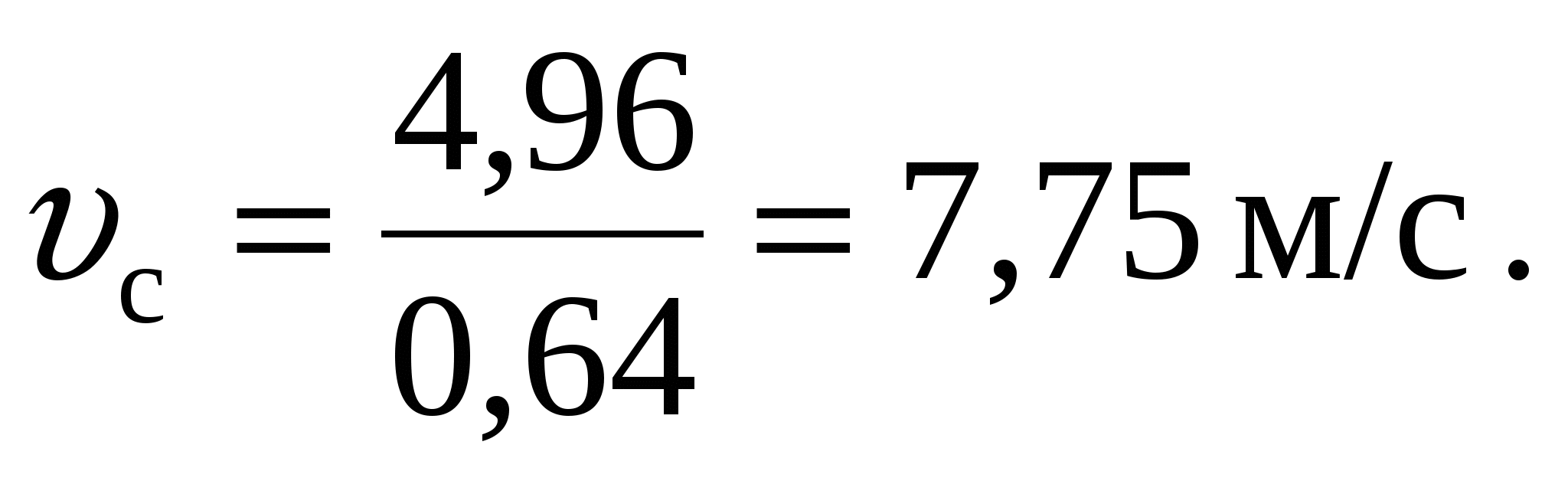
Для определения давления рс составим уравнение Бернулли для двух сечений 0-0 и С-С при плоскости сравнения, проходящей через ось насадка О'- О' (рис. 11) [4]
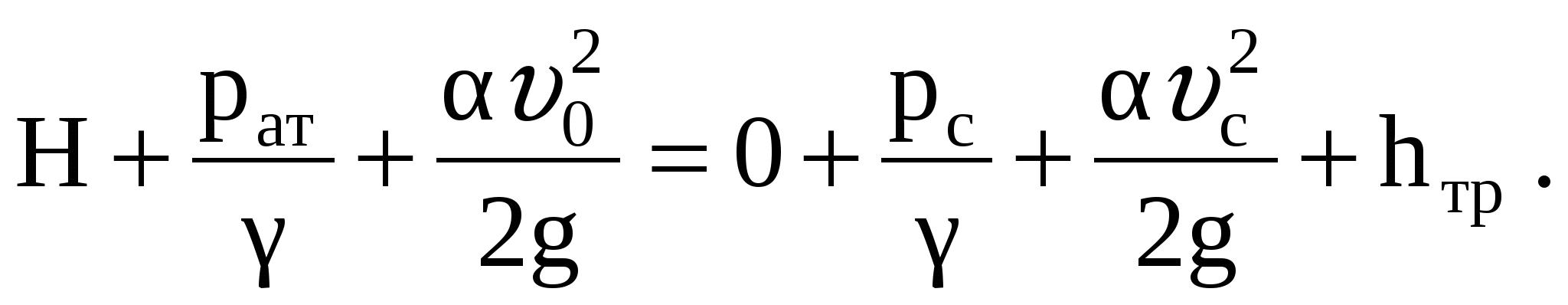
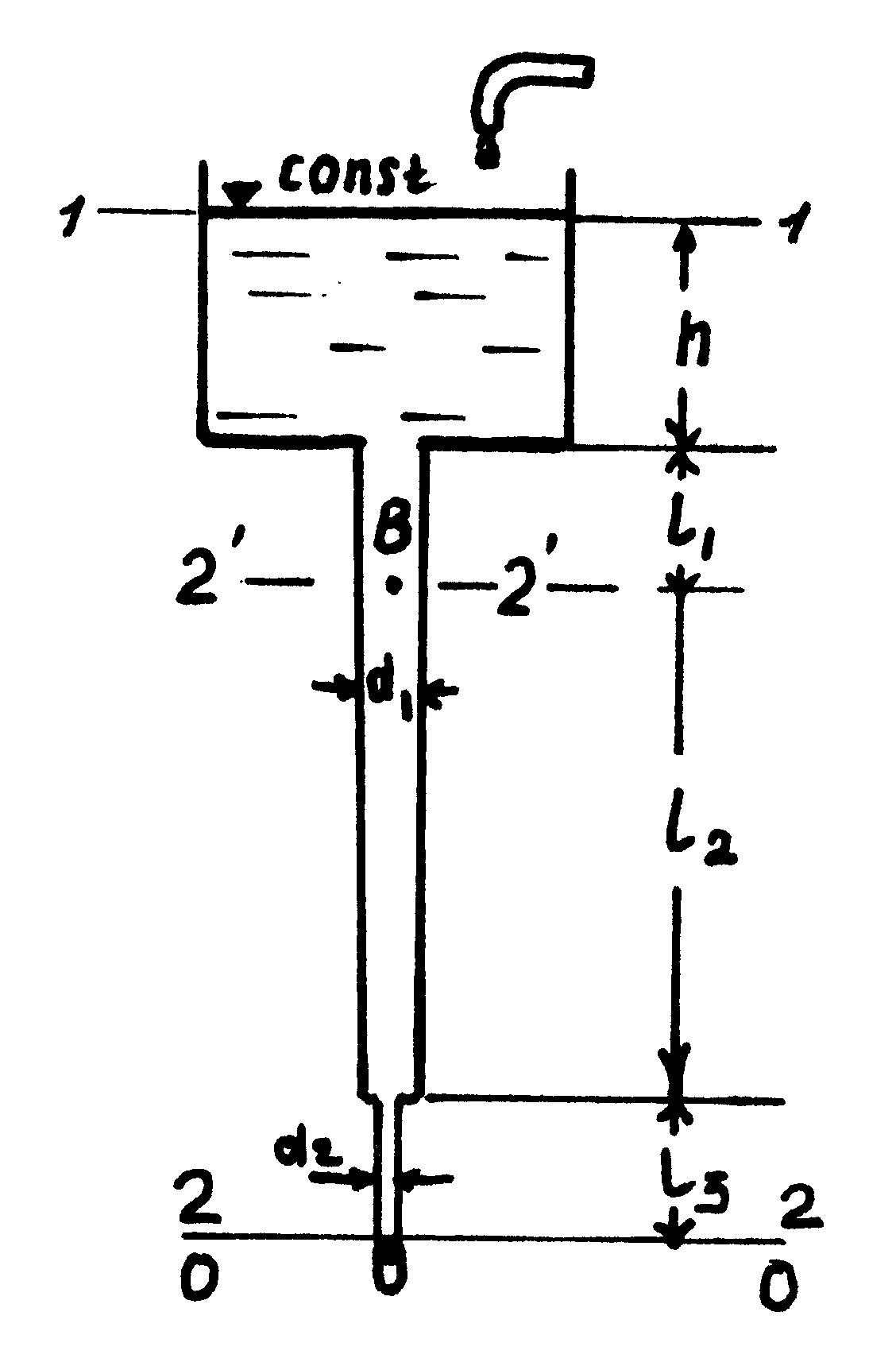
Рисунок 11
Так как при движении жидкости между сечениями О-О и С-С будут потери только на сопротивление в тонкой стенке, то 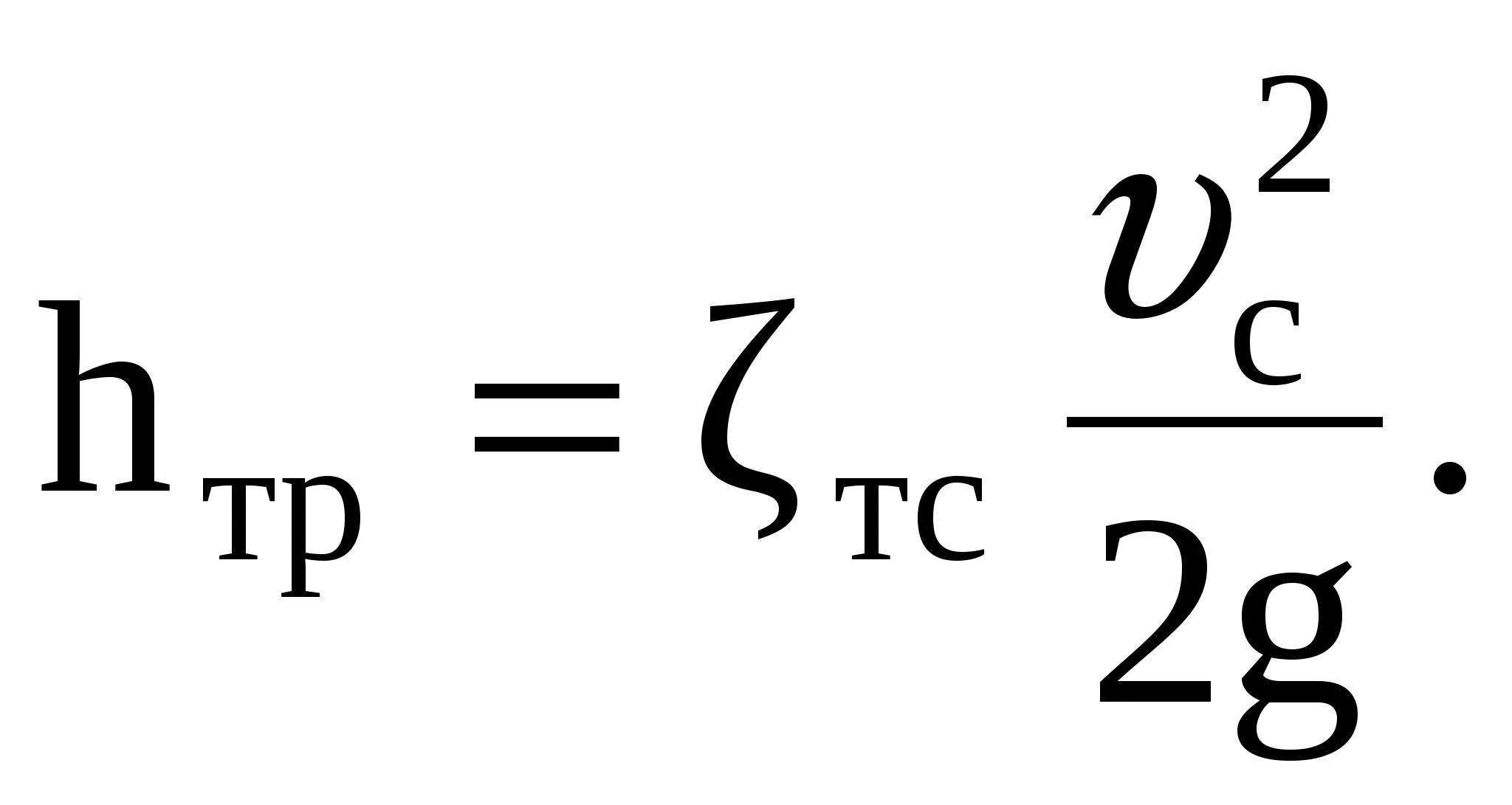 Полагая Полагая 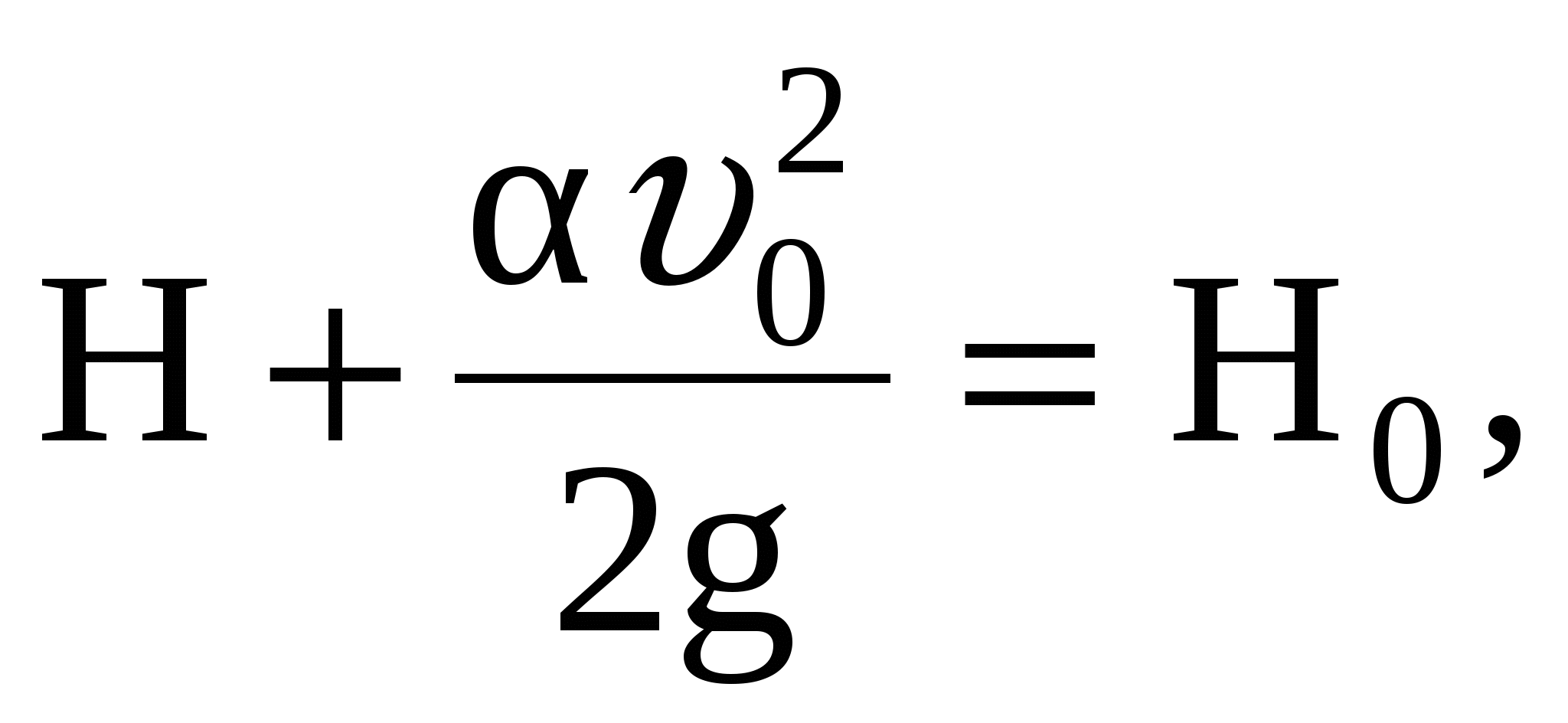 имеем имеем
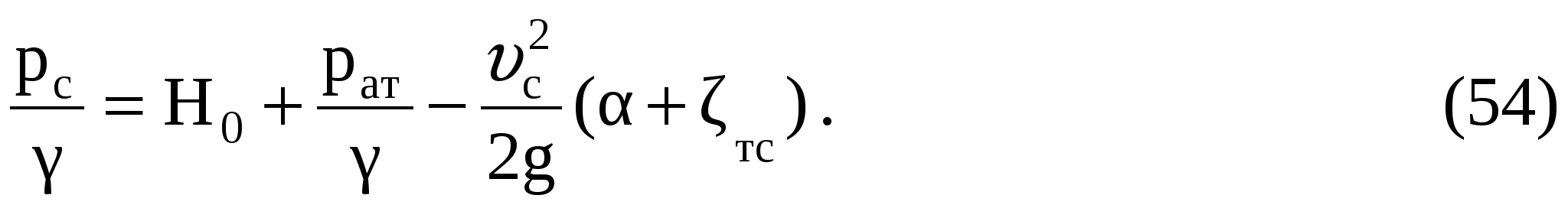
Подставляя численные значения, получим высоту давления h:
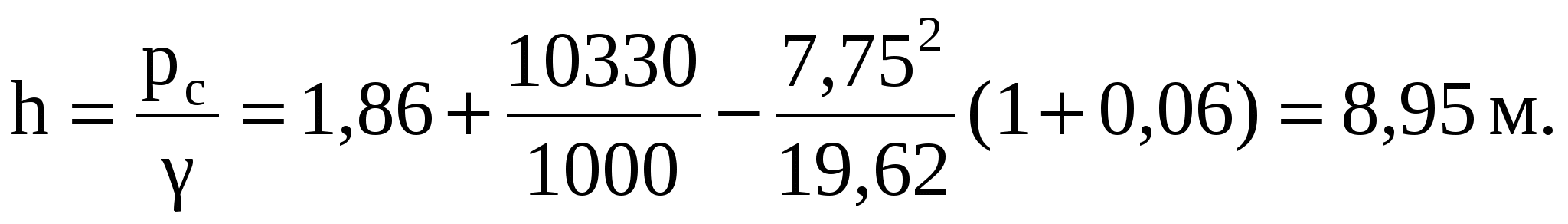
Давление рс = h g = 10008,959,81 = 0,0878 МПа.
Недостаток до атмосферного давления в сжатом сечении
Рвак = pат – pс = 0,101 – 0,0878 = 0,0132 МПа.
Высота вакуума, выраженная в сантиметрах водяного столба,


Такой же результат получим, применив формулу

Задача 3.2. Определить расход жидкости из резервуара через два цилиндрических насадка и величину вакуума в них. Один насадок расположен горизонтально в боковой стенке резервуара на расстоянии е = 20 см от дна, другой – вертикально в дне резервуара (рис. 12). Размеры насадков одинаковы: d = 6см, l = 20 см. Глубина воды в резервуаре h = 100 см.
Решение. 1. Напор над центром горизонтального насадка Н1 = h – е = = 100 – 20 = 80 см.
Пренебрегая скоростью подхода, так как размеры резервуара достаточно велики, примем Н1 = Н0.
Расход из горизонтального насадка [5]


Вакуум в сжатом сечении горизонтального насадка hвак = 0,74Н0 = = 0,740,8 = 0,59 м.
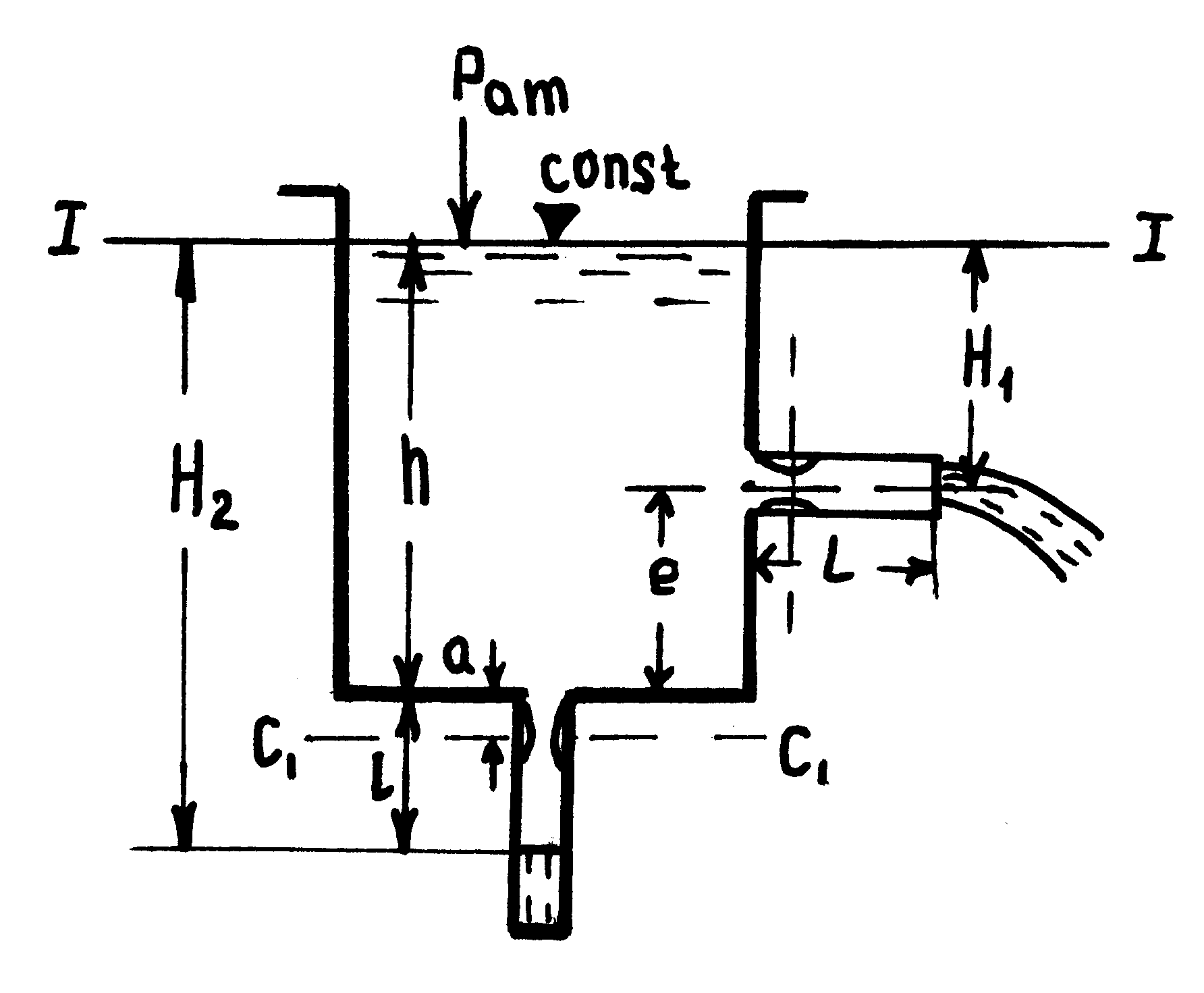
Рисунок 12
2. Расход через насадок, расположенный в дне резервуара, соответствует напору H2 = h+l = Н0. Скоростью подхода, как и в первом случае, пренебрегаем
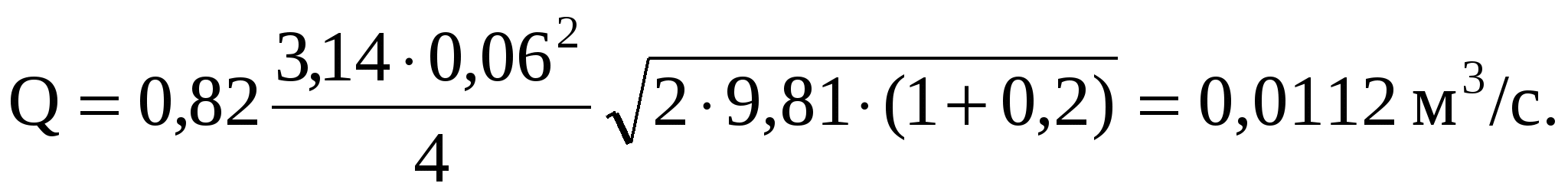
Расход из резервуара через оба насадка равен Q = 0,00918 + 0,0112 = = 0,0204м3/c.
Для определения вакуума в сечении C1-C1 составим уравнение Бернулли для сечений 1-1 и C1-C1, взяв плоскость сравнения на уровне C1-C1,
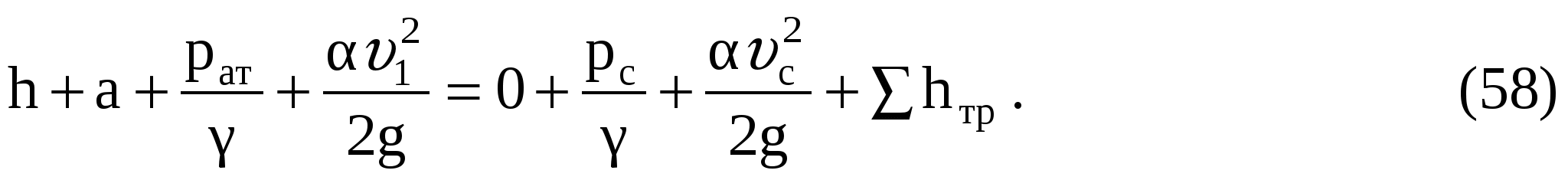
Отсюда, принимая потери h на сопротивление тонкой стенки, получим выражение высоты вакуума
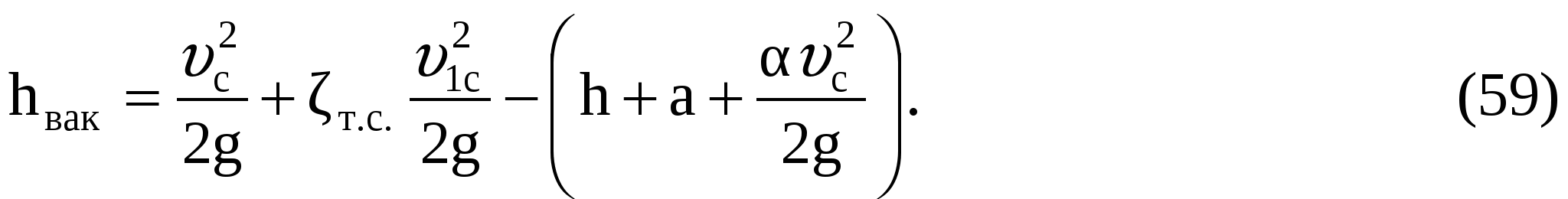
или

Полагая 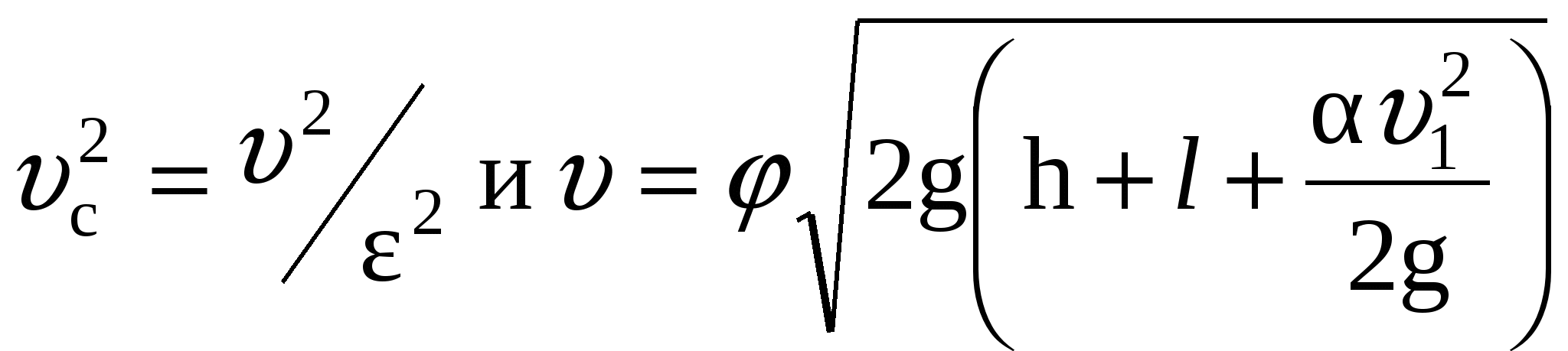 , получим: , получим:
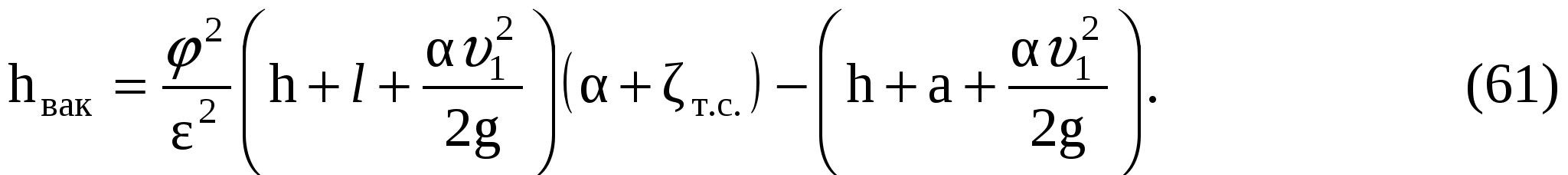
Подставляя числовые значения величин = 0,82, = 0,64, т.с.= 0,06, = 1, 1 0 и принимая а
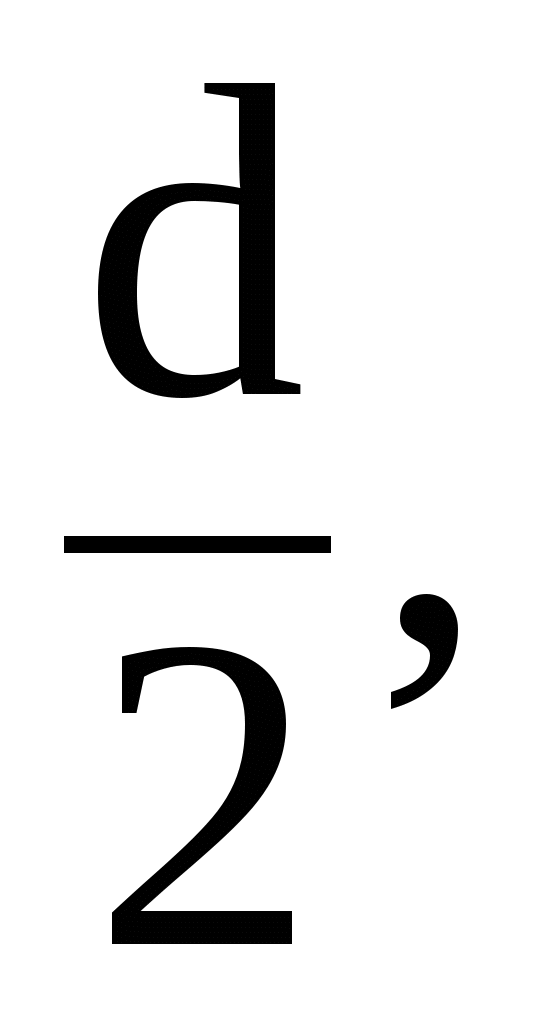 будем иметь: будем иметь:
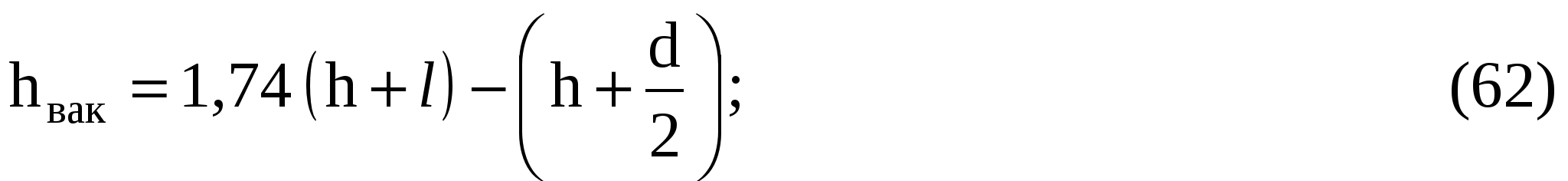
или 
Для условий задачи величина вакуума в вертикальном насадке будет
hвак = 0,741,2 + 0,2 – 0,03 = 1,06 м
Задача 3.3. В теле железобетонной плотины проектируется водоспуск в виде трубы длиной l = 5,0 м (рис. 13). Напор над водоспуском при свободном истечении равен H1 = 6,5 м. Разность отметок уровней воды в верхнем и нижнем бьефах плотины H2 = 15,0 м. Скорость подхода воды к плотине 0 = 0,4 м/с. Определить диаметр d водоспуска, если расход Q = 12,0 м3/с. Кроме того, установить:
а) какой будет расход Q1 через водоспуск, если уровень нижнего бьефа поднимется на 10 м;
б) на какой глубине H1 относительно уровня верхнего бьефа следует расположить водоспуск, чтобы он пропускал наибольший расход (при свободном истечении).

Рисунок 13
Решение. Скоростной напор при = 0,4 м/с равен
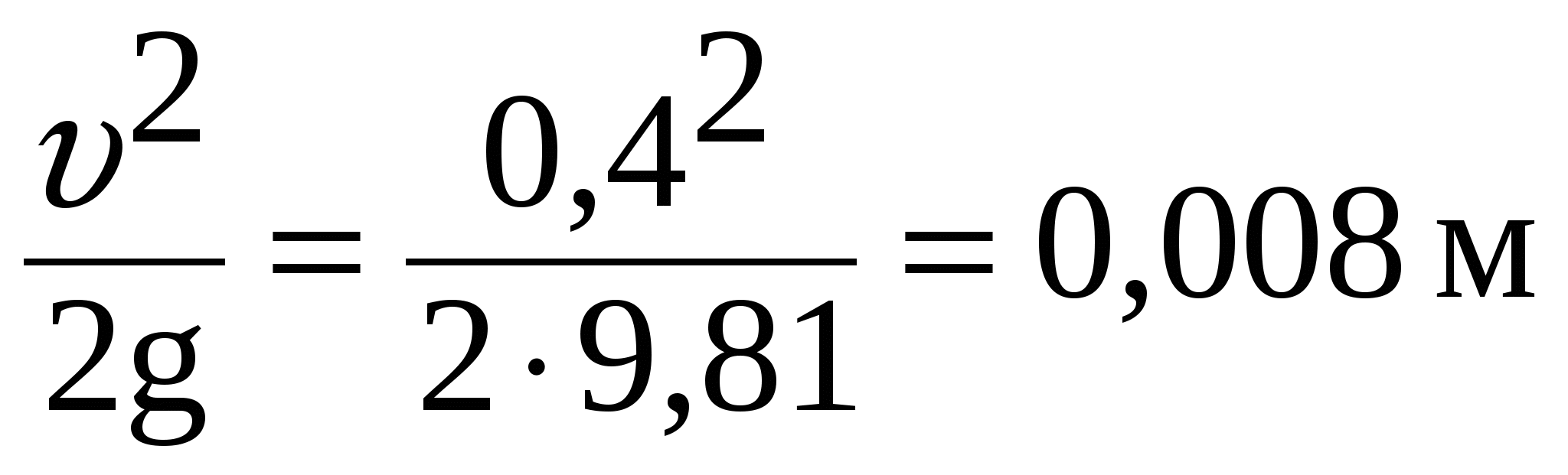 , поэтому полагаем напор H0 , поэтому полагаем напор H0
H1.
Из уравнения (64) определим площадь водоспуска , м2, считая, что он будет работать как насадок с коэффициентом расхода = 0,82


При = 1,3 м2 диаметр будет d = 1,29 м.
Соотношение между диаметром водоспуска и его длиной соответствует случаю насадка: 4d = 41,29 = 5,16 м
водоспуска. Следовательно, коэффициент = 0,82 применен правильно.
а) При повышении уровня нижнего бьефа на 10 м водоспуск будет работать как затопленный насадок при напоре Н = 15 – 10 = 5,0 м.
Расход в этом случае

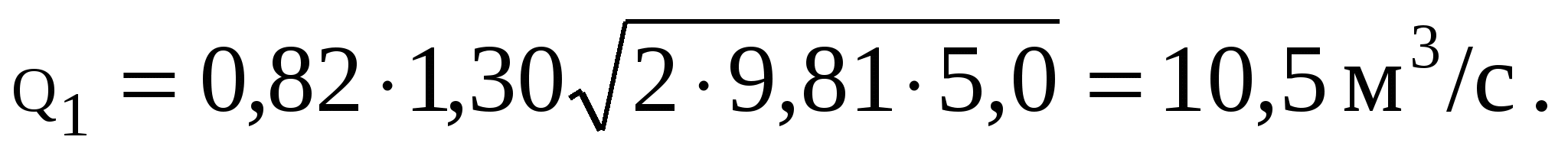
б) Водоспуск при расчетном диаметре d = l,29 м пропустит наибольший расход в том случае, когда будет обеспечен наибольший напор. При заданной схеме наибольший напор Нмакс = 15 м, т. е. ось водоспуска следовало бы расположить на уровне нижнего бьефа. Однако при напоре Н = 15 м вакуум в насадке достиг бы высоты hвак = 0,74; Н = 0,7415 = = 11,1 м, т. е. большей, чем составляет одна атмосфера. Практически допустимый вакуум, при котором может быть обеспечена устойчивая работа водоспуска, принимается Нвак = 9,0-9,5 м. Отсюда предельный напор перед водоспуском должен быть
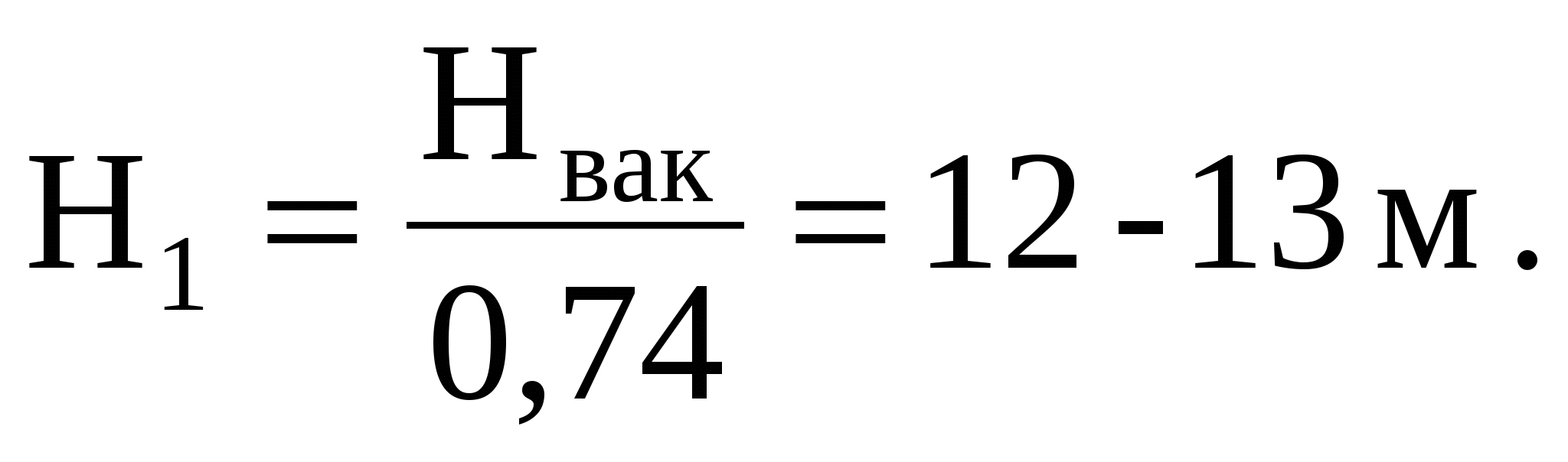
При этом расход через водоспуск равен

Задача 3.4. Цилиндрический бак с площадью = 3,0 м2 и высотой Н1 = 4,0 м, заполненный до краев водой, нужно опорожнить за время t = 5,0 мин.
Определить необходимую для этого площадь двух одинаковых отверстий, одно из которых расположено в центре дна, другое в стенке, на половине высоты бака (рис. 14).
Решение. Время опорожнения верхней половины бака определится из дифференциального уравнения [7]:

откуда

Освобождаясь от иррациональности в знаменателе и подставляя пределы при опорожнении верхней половины резервуара, получим
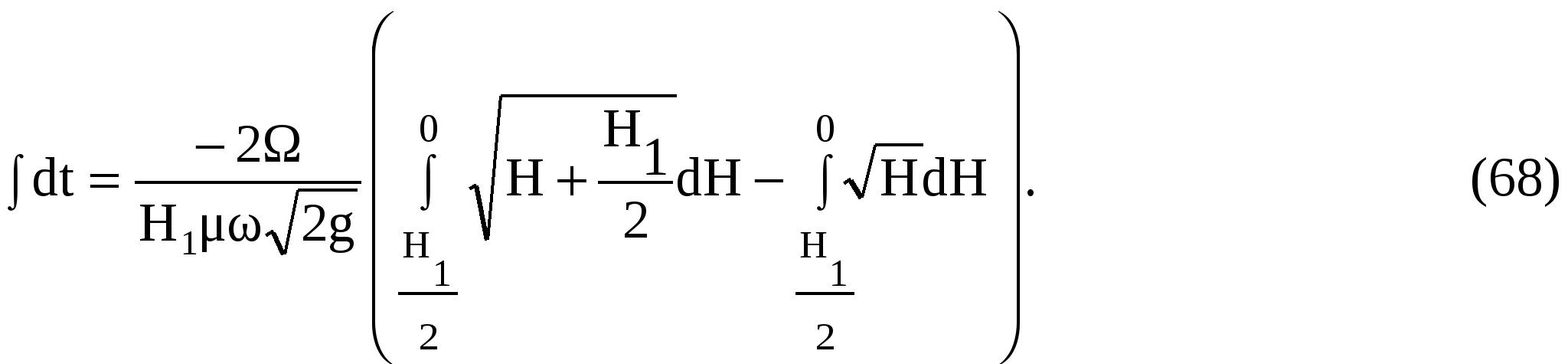
Вводя переменную у = Н + Н1/2, пределы которой будут от Н1 до Н1/2, запишем:
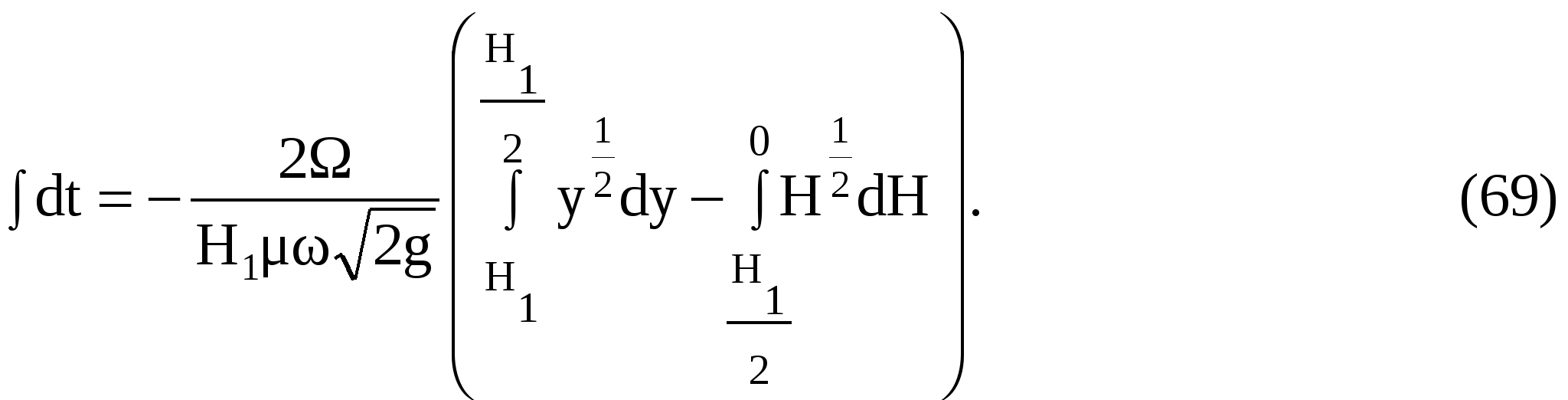
В результате интегрирования получим t1, c – время опорожнения верхней половины бака

Время опорожнения нижней половины бака t2, c, определится по формуле

По условию задачи t1 + t2 = t = 560 = 300 c.
Подставляя числовые значения, получим:
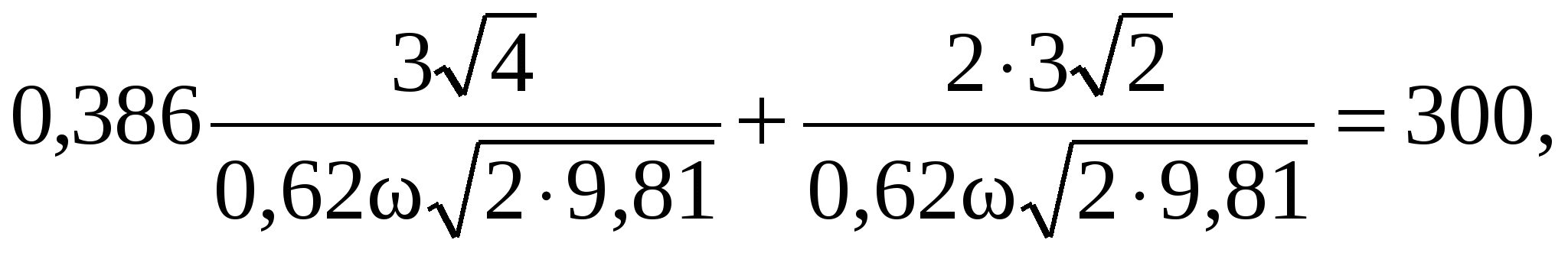
откуда = 0,0131 м2.
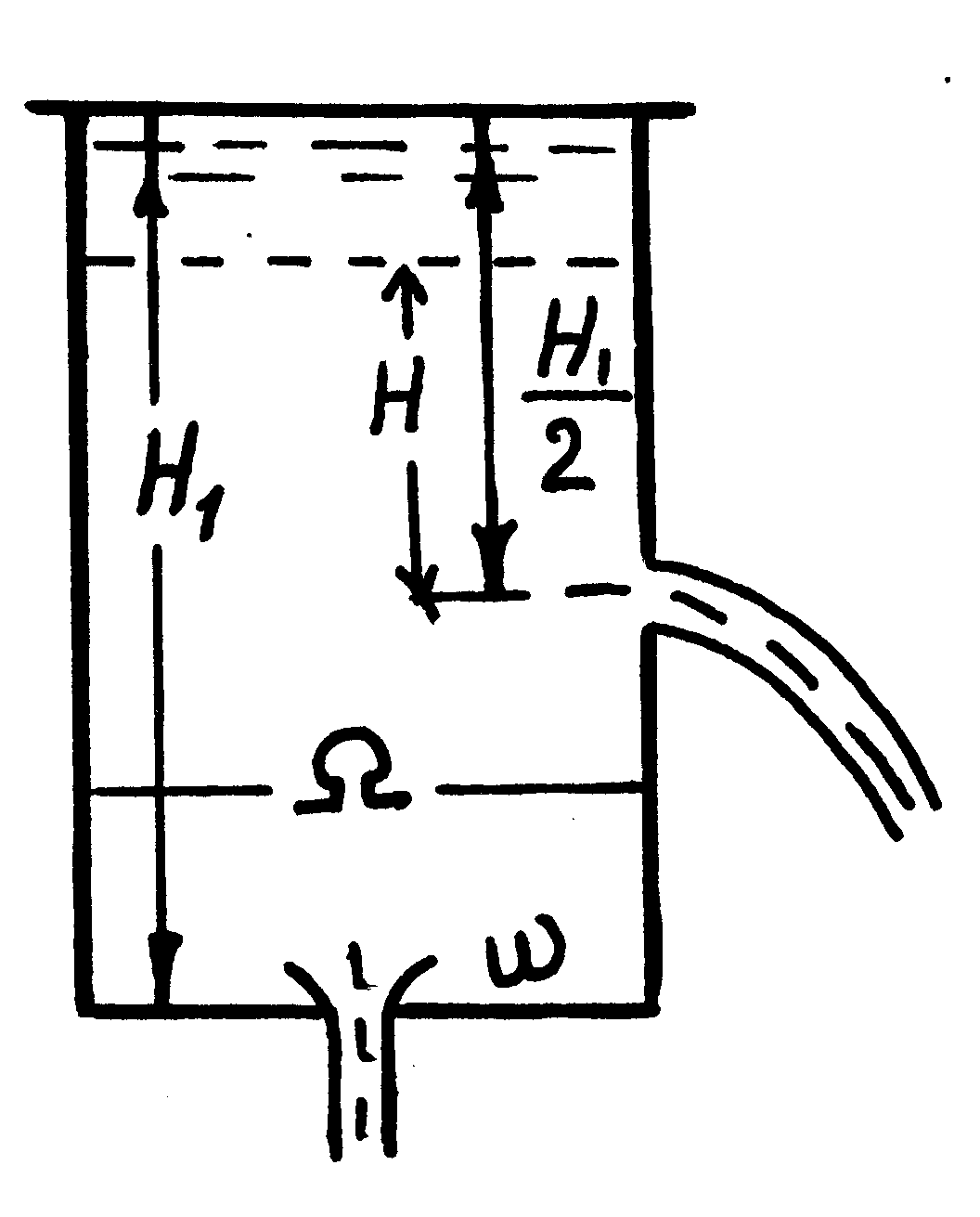
Рисунок 14
Задача 3.5. Определить время t опорожнения цилиндрического резервуара, заполненного водой, имеющего диаметр d = 2,4 м и высоту l = 6,0 м для двух случаев (рис. 15):
а) Резервуар поставлен вертикально. Отверстие = 0,0176 м2расположено в дне.
б) Резервуар лежит горизонтально. Отверстие = 0,0176 м2 расположено на боковой поверхности внизу.
В обоих случаях при истечении обеспечен доступ воздуха в резервуар.

Рисунок 15
Решение. В первом случае будет истечение из отверстия при переменном напоре от H1 = l до H1 = 0, при постоянной площади поперечного сечения
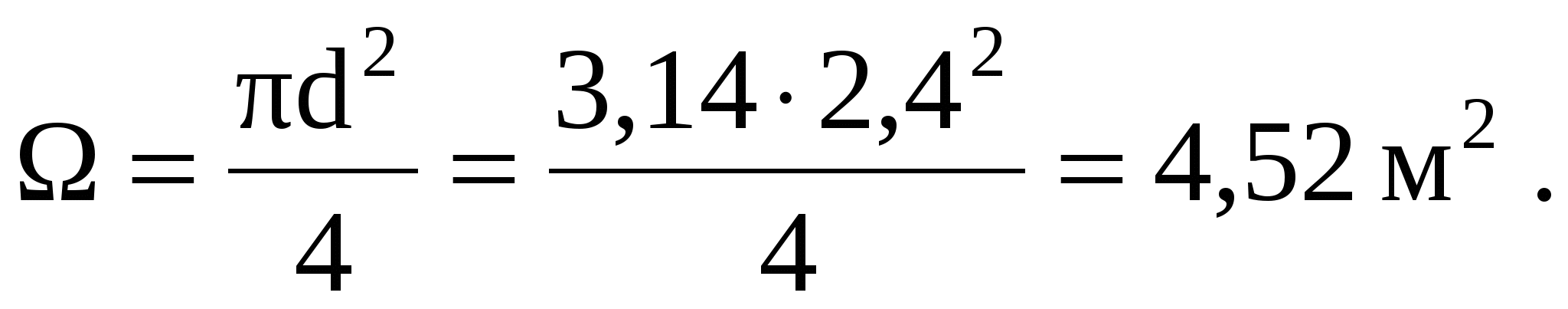
Время опорожнения определяем по уравнению [3] (72), принимая = 0,62,

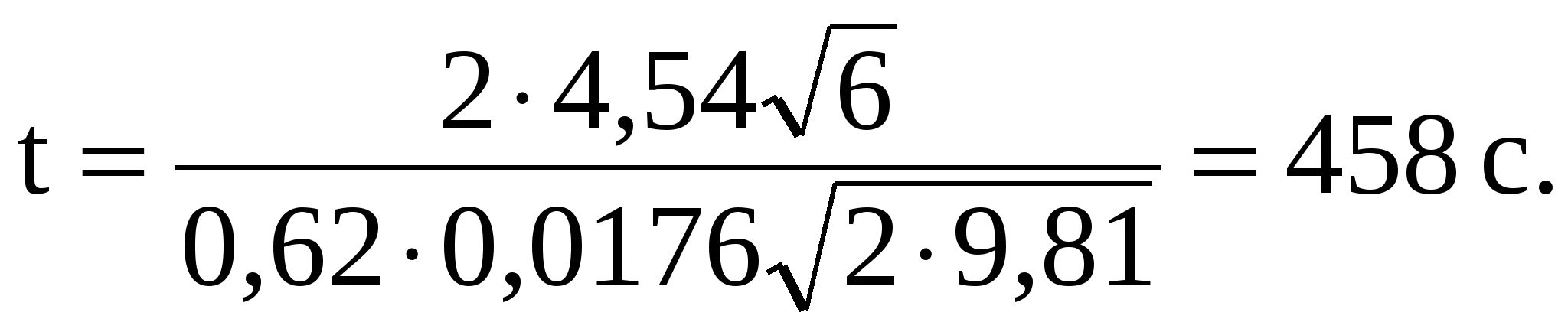
Во втором случае уравнение (72) для определения времени опорожнения неприменимо, так как площадь является переменной, зависящей от величины напора Н.
Из отверстия за время dt вытекает

За то же время объем воды в резервуаре уменьшается на
– dH.
Тогда из равенства
– dH = 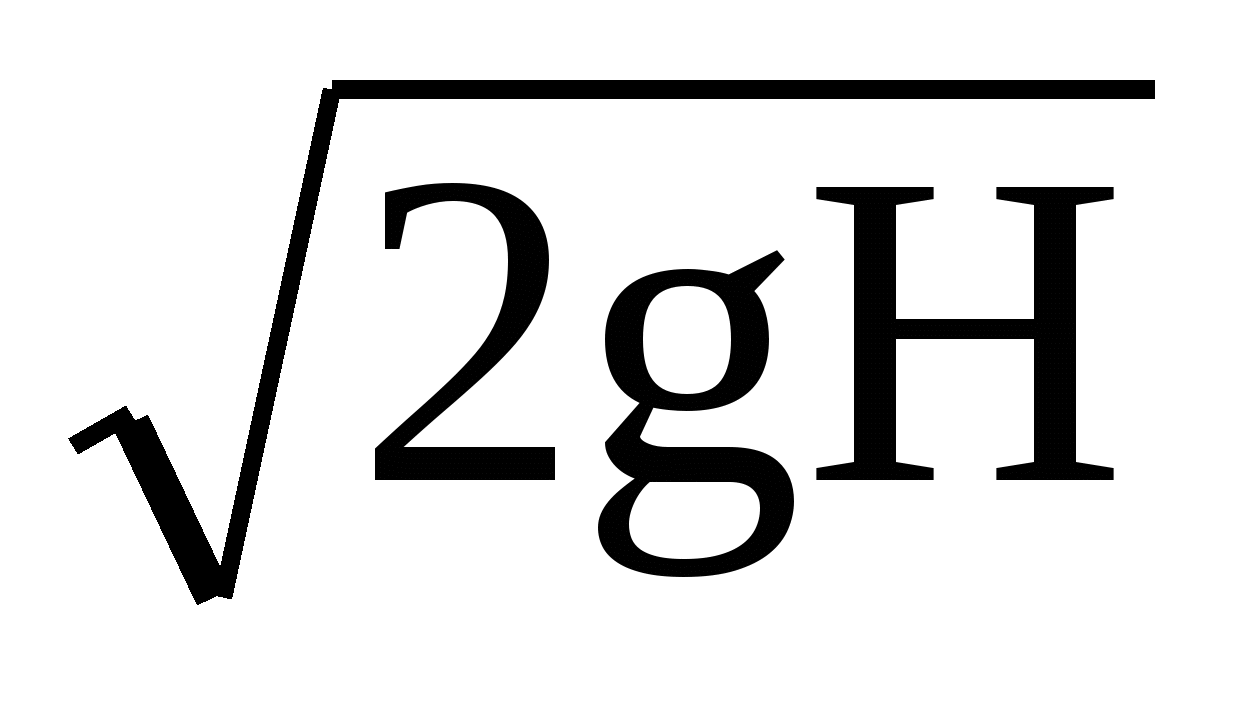 dt dt
получим:

Выразим переменную как функцию H. Площадь = lx при опорожнении сначала увеличивается от = 0 до = ld, затем уменьшается от = ld до = 0.
Как следует из рисунка 15
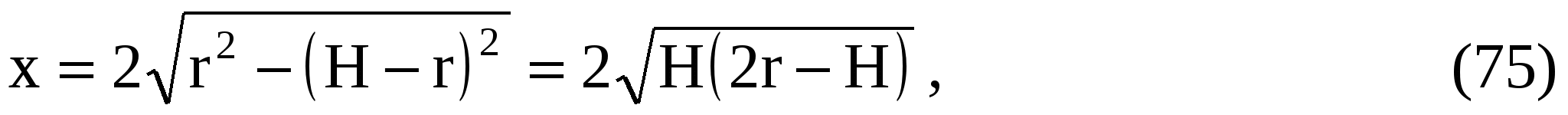
тогда

Подставляя значение площади в уравнение (75), имеем:
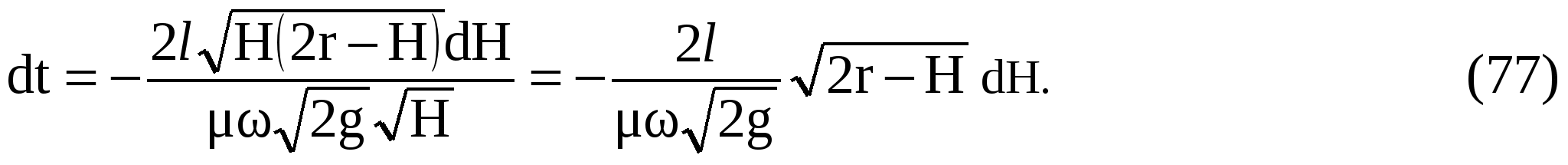
Напишем интеграл в пределах от Н1 = 2r до Н2 = 0

Введем новую переменную у = 2r–H, при этом dy = -dH. Пределы изменения у будут от y1 = 0 до y2 = 2r.
Имеем
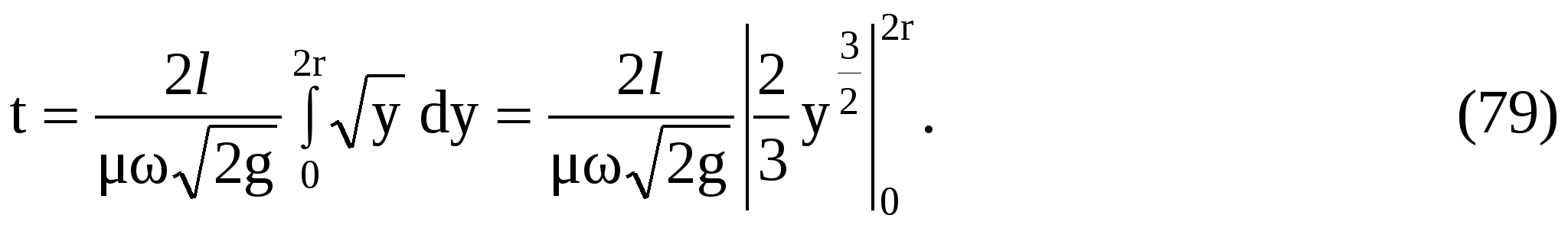
Подставляя пределы, получим

Для численных значений задачи

Задача 3.6. На рисунке 16 приведен план водохранилища с показанием горизонталей через 1 м и график зависимости площади зеркала водохранилища от его глубины. В водохранилище из реки поступает постоянный расход Qo = 4,16 м3/с. Определить время Т опорожнения водохранилища от отметки 36,0 до отметки 31,0 м. если площадь отверстия в плотине, через которое свободно вытекает вода из водохранилища, составляет = 11,0 м2. Центр отверстия расположен на отметке 30,0 м. Коэффициент расхода отверстия принять = 0,7.

Рисунок 16
Решение. Приток в водохранилище за время dt будет Q0dt. Расход из водохранилища за то же время  . Изменение объема воды в водохранилище dH равно разности притока и расхода . Изменение объема воды в водохранилище dH равно разности притока и расхода
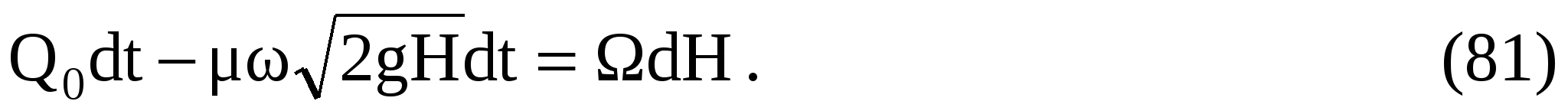
Отсюда время t, в течение которого глубина в водохранилище изменится от H1 до H2 при наличии постоянного притока Q0, будет

При опорожнении водохранилища H1 > H2, поэтому перепишем интеграл (считая = const) так:
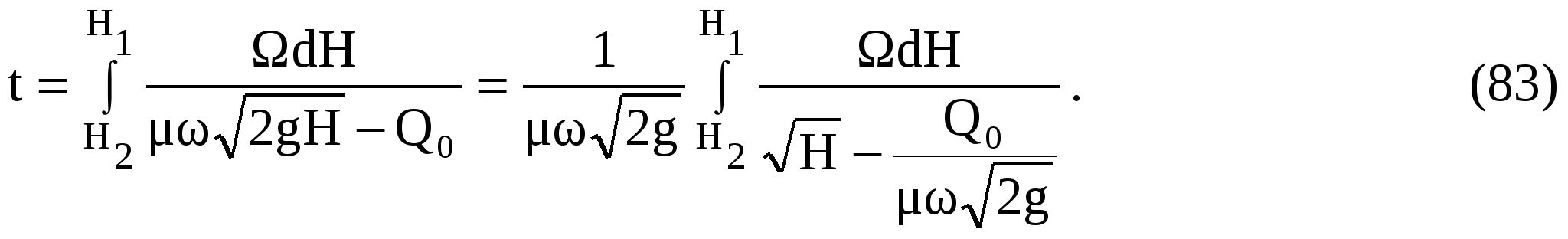
Точное интегрирование этого уравнения невозможно, так как нельзя выразить аналитически через Н, ввиду неправильной формы водохранилища. Заменим интегрирование одним из приближенных приемов – суммированием по способу трапеций.
Разделим опорожняемый объем водохранилища от отметки 36,0 м до отметки 31,0 м на n = 5 частей через  Н = 1 м по высоте. Объем одной части (приближенно) Н = 1 м по высоте. Объем одной части (приближенно)

Заменяя в подынтегральном выражении дифференциал dН конечной разностью напоров, получим выражение для времени при изменении напоров от начального Нn до конечного H1 (здесь Нn = 6м, H1 = l м):
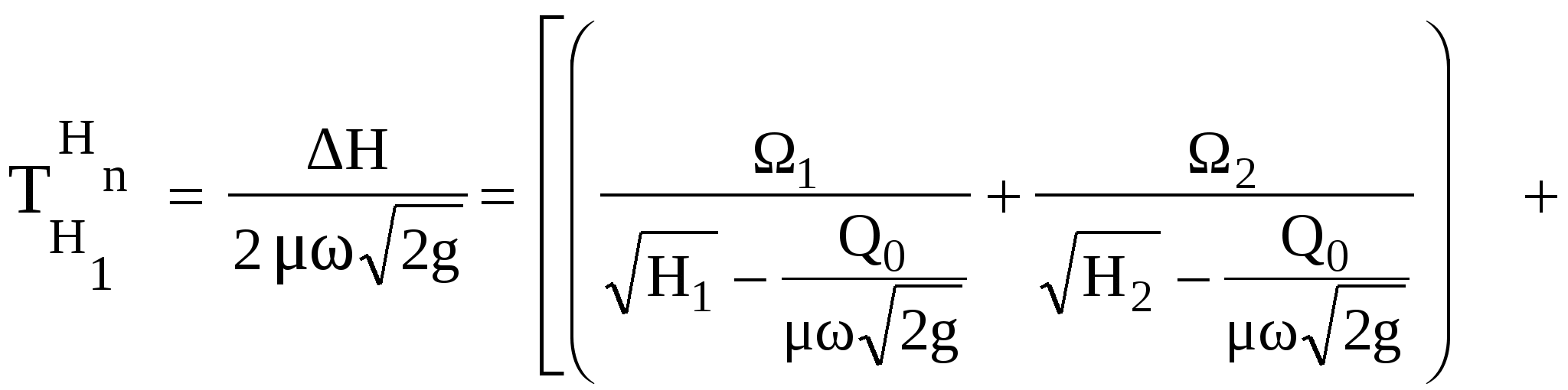
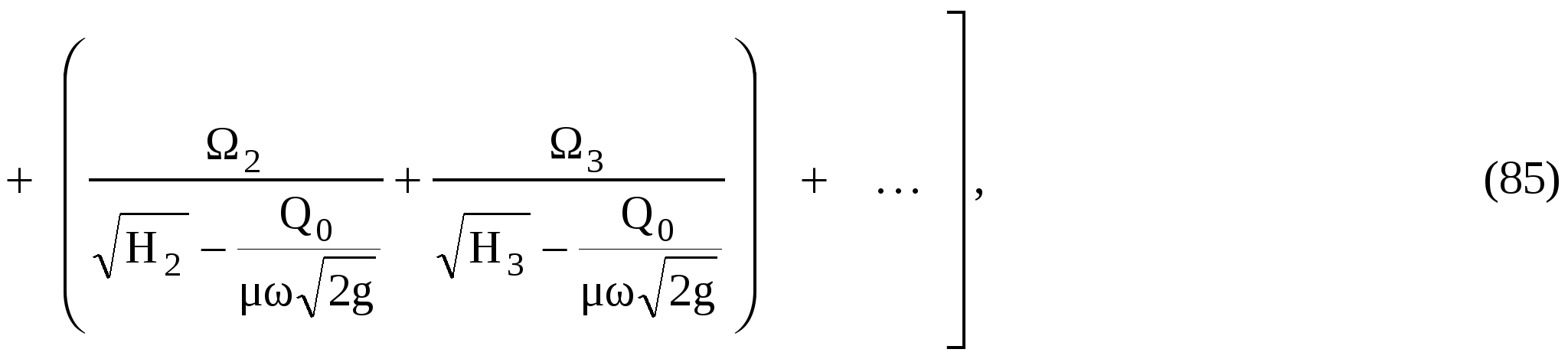
или
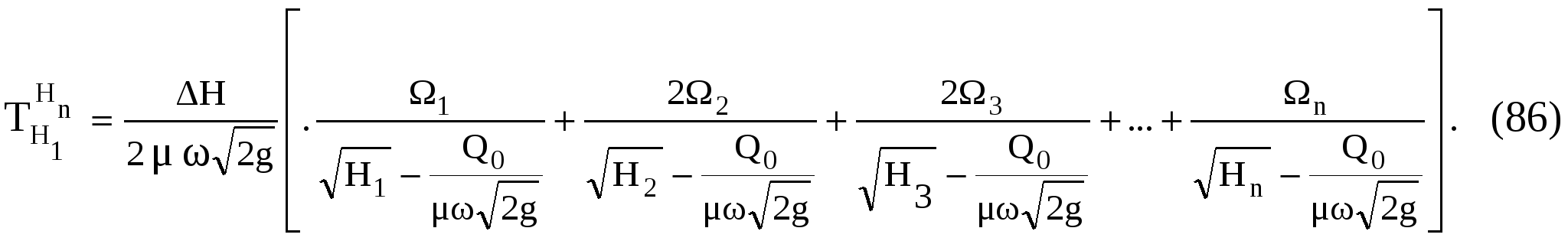
Подставляя в последнее уравнение численные значения задачи, получим, подсчитав предварительно
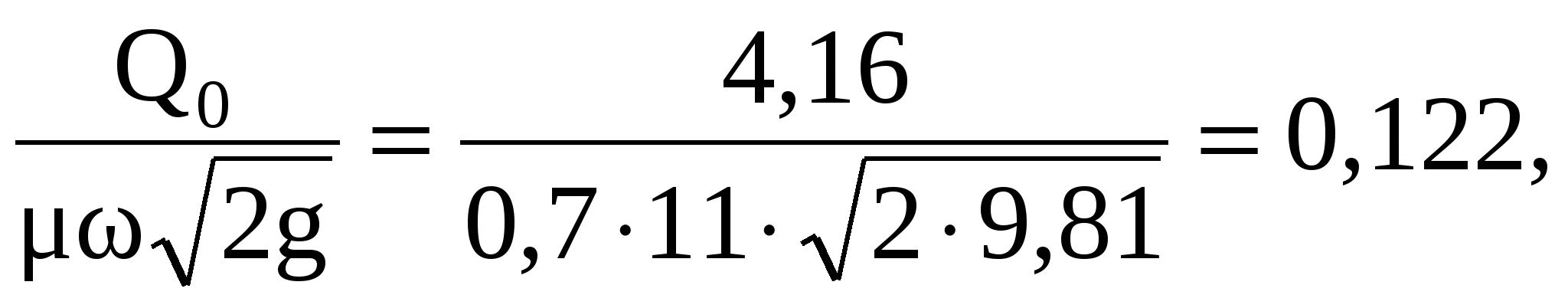

|
 Скачать 1.79 Mb.
Скачать 1.79 Mb.

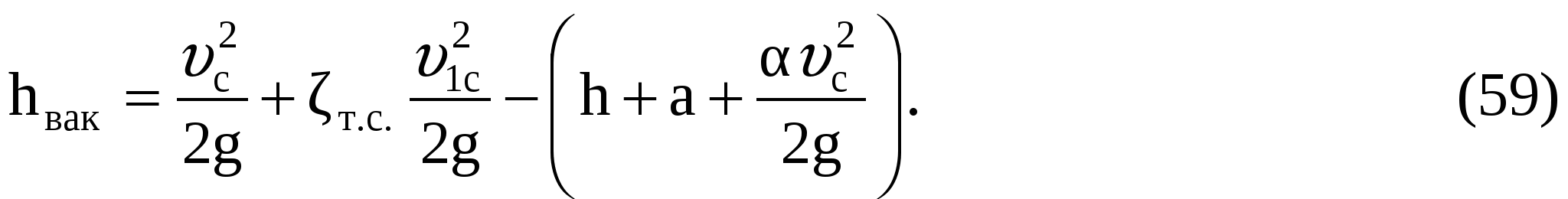

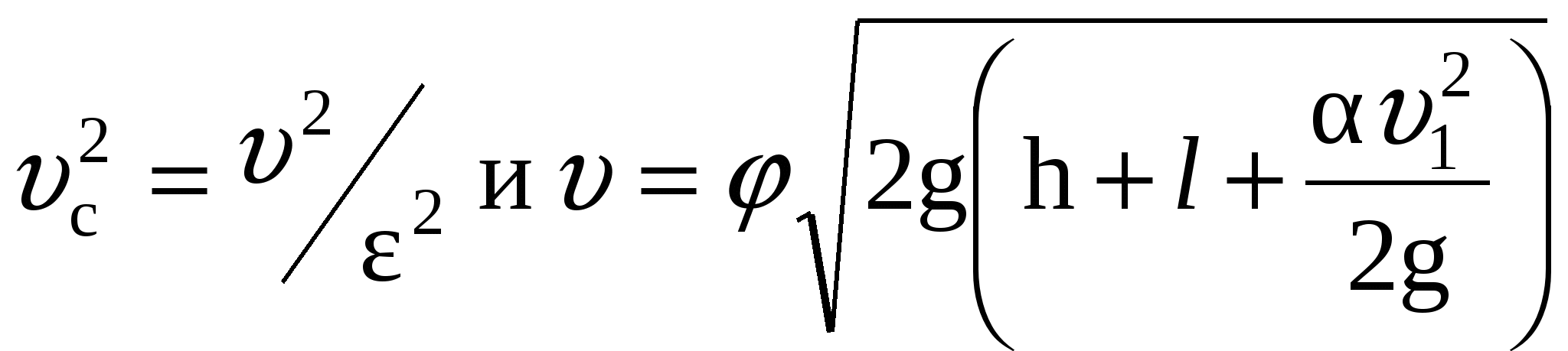 , получим:
, получим: