Сборник задач по практикам. Сборник задач по гидравлике может использоваться в качестве учебного пособия для практических занятий по курсу гидравлики и являться дополнением к лекционному курсу

• Название: Сборник задач по гидравлике может использоваться в качестве учебного пособия для практических занятий по курсу гидравлики и являться дополнением к лекционному курсу
• Анкор: Сборник задач по практикам.doc
• Дата: 27.08.2018
• Размер: 1.79 Mb.
• Имя файла: Сборник задач по практикам.doc
• Тип: Сборник задач; #23634
• страница: 8 из 12

7 ГИДРАВЛИЧЕСКИЙ ПРЫЖОК

Задача 7.1. Прыжок возникает в трапецеидальном русле при Q = 16 м³/с, b = 7 м; m = 1,5. Определить сопряженную глубину h", если h' = 0,5 м.

Решение. Определим h" по вспомогательным рисункам 1 и 2 в приложении А. Для этого находим: и Вычисляем параметр z'. и по графику k=2,24 м. Тогда h"= k h'=2,240,5 =1,12 м.

Так как отношение больше двух, то имеет место совершенный прыжок и решение правильное.

Задача 7.2. В параболическом русле возникает прыжок со вто­рой сопряженной глубиной h" = 2,2 м. Найти первую сопряженную глубину h' и длину прыжка _п, если Q = 6,2 м³/с, а р = 2,6 м.

Решение. Вычисляем величину и находим 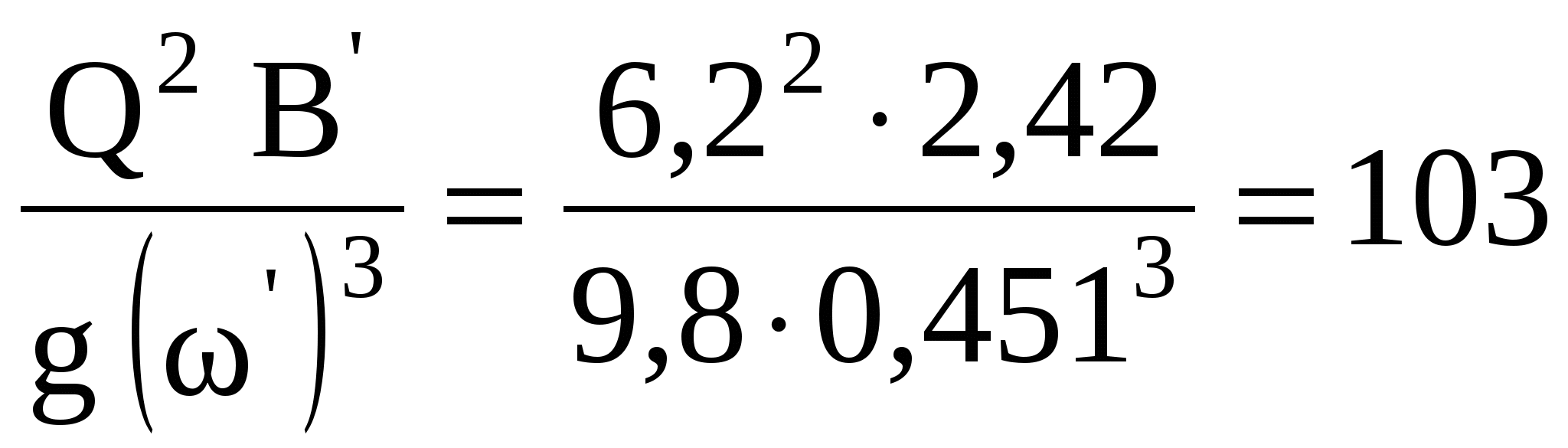'= По таблице приложения Б находим соответствующее значение '=0,275. Тогда h'= м. Далее вычисляем П'_к, для чего находим

В'= м и

.

Тогда П'_к=.

По формуле Айвазяна О.М.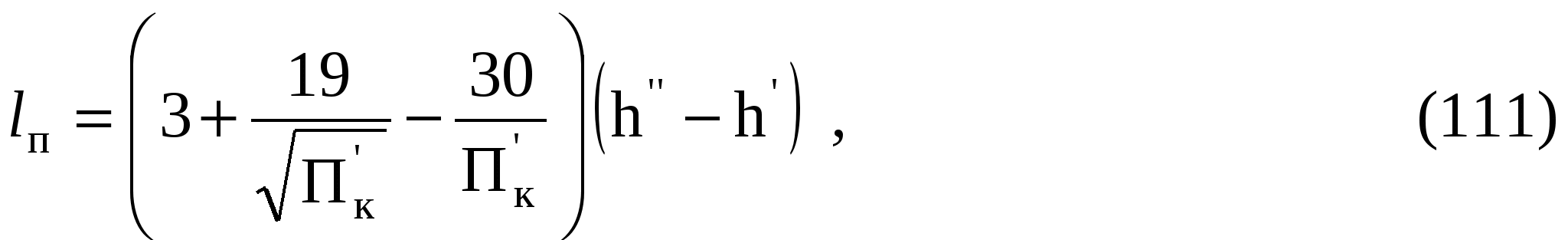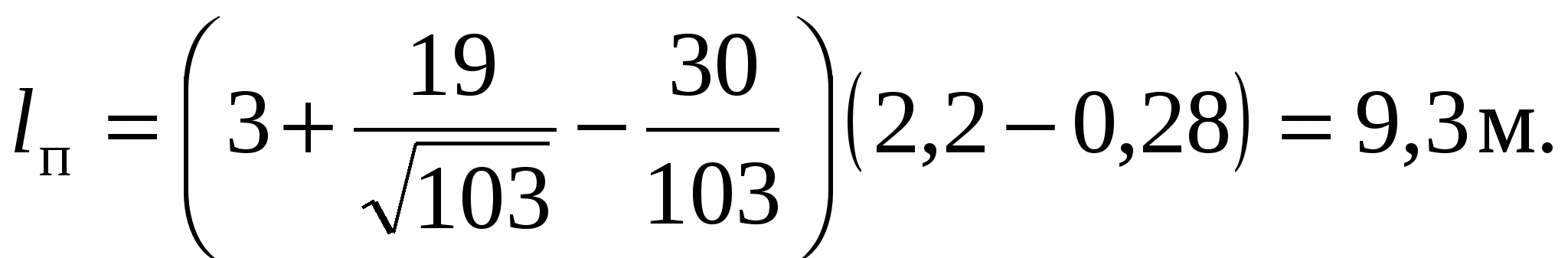





Задача 7.3. Определить вторую сопряженную глубину гидрав­лического прыжка в круговом (сегментном) русле, если первая со­пряженная глубина h' = 0,4м, a Q = 5 м³/с и r = 2 м.

Решение. Определяем безразмерную величину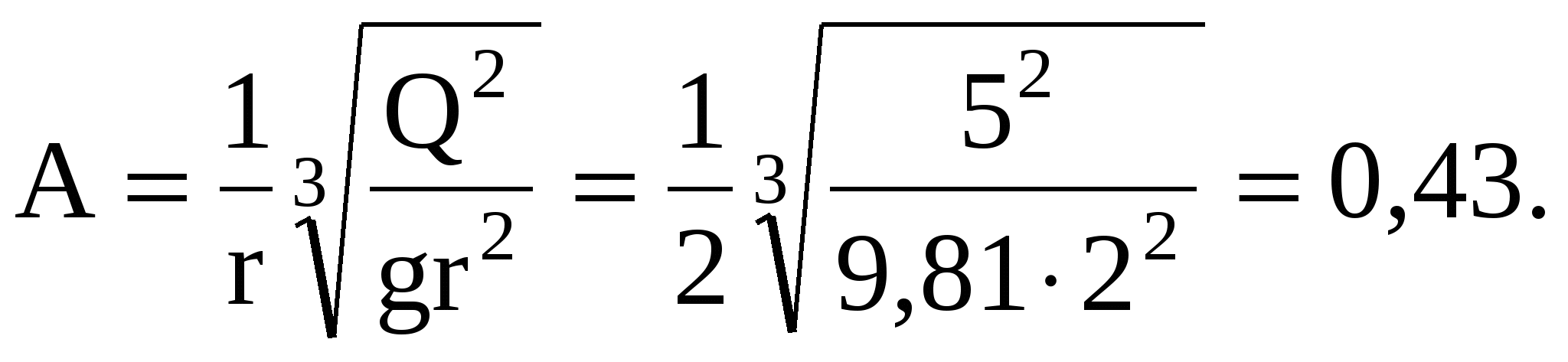



Далее находим отношение и по (рис. 3 приложения А) находим отношение при параметре кривой 0,43. Получаем = 0,84, откуда h" = 0,842 = 1,68 м.

Задача 7.4. Установить характер сопряжения потоков в пря­моугольном лотке шириной b = 10 м при изменении уклона от ₁ = 0,05 до ₂ = 0,00078, если Q = 20 м³/с, а нормальные глубины рав­ны соответственно = 0,29 м; = l,09м.

Решение. Определим критическую глубину для рассматриваемых условий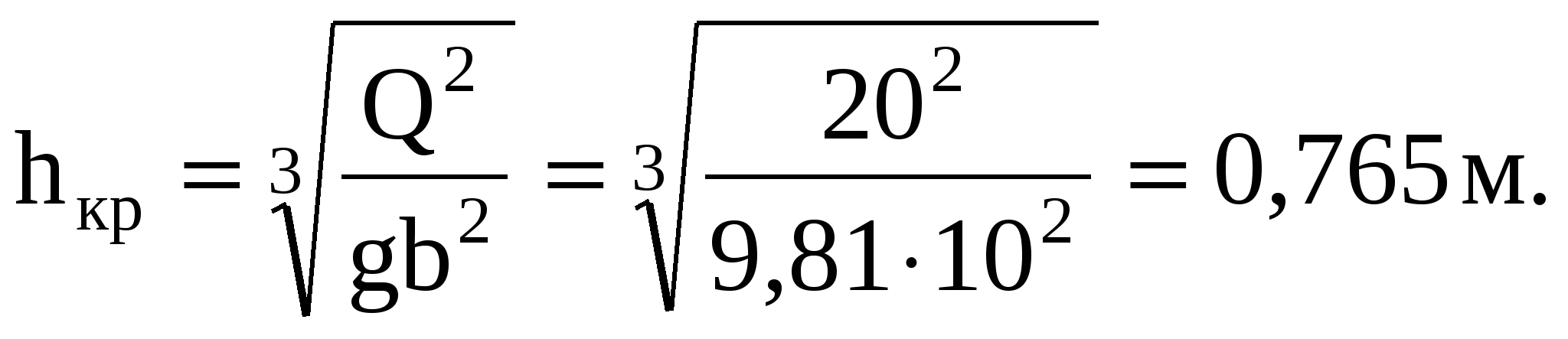

Так как нормальная глубина на первом участке меньше крити­ческой, а на втором участке больше критической, то приходим к вы­воду, что на верхнем участке поток в бурном состоянии, а на ниж­нем – в спокойном. Следовательно, сопряжение потоков произой­дет в форме гидравлического прыжка.

Уточним вид и место прыжка.

Определим значение глубины , сопряженной с , считая, что до конца первого участка поток движется с нормальной глу­биной .

Сравниваем 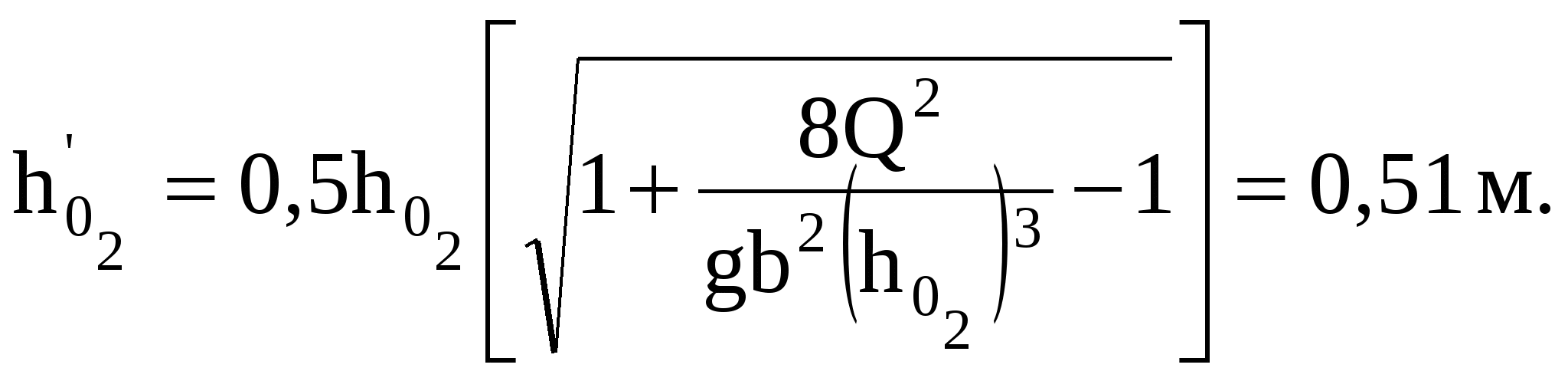с нормальной глубиной на втором участке и убеждаемся, что > . Следовательно, в месте перелома уклона прыжок возникнуть не может. Тем более он не может воз­никнуть на первом участке. Остается только, что прыжок возни­кает на втором участке в некотором удалении от точки перелома уклона, там, где глубина достигает значения . Найдем :



Таким образом, на втором участке будет сначала кривая под­пора, на длине, необходимой для увеличения глубины от 0,29 м до 0,51 м. Затем произойдет прыжок от глубины 0,51 м до 1,09 м, и далее поток будет двигаться равномерно с глубиной = 1,09 м. На первом участке сохранится равномерное движение с глубиной = 0,29 м по всей длине первого участка.