Сборник задач по практикам. Сборник задач по гидравлике может использоваться в качестве учебного пособия для практических занятий по курсу гидравлики и являться дополнением к лекционному курсу

• Название: Сборник задач по гидравлике может использоваться в качестве учебного пособия для практических занятий по курсу гидравлики и являться дополнением к лекционному курсу
• Анкор: Сборник задач по практикам.doc
• Дата: 27.08.2018
• Размер: 1.79 Mb.
• Имя файла: Сборник задач по практикам.doc
• Тип: Сборник задач; #23634
• страница: 2 из 12

1 ГИДРОСТАТИКА

Задача 1.1. Жидкостный манометр. В замкнутом сосуде с водой (рис. 1) абсолютное давление на сво­бодной поверхности р = 0,122625 МПа. На какую высоту Н поднимется вода в открытой трубке, сообщающейся с сосудом на глубине h = 3 м под свободной поверх­ностью?

Решение. Давление в точке А, создаваемое высотой водя­ного столба H, вместе с давлением атмосферы в открытой трубке должно быть равно давлению в той же точке с внутренней стороны сосуда, создаваемому водяным столбом высотой h и давлением p₀.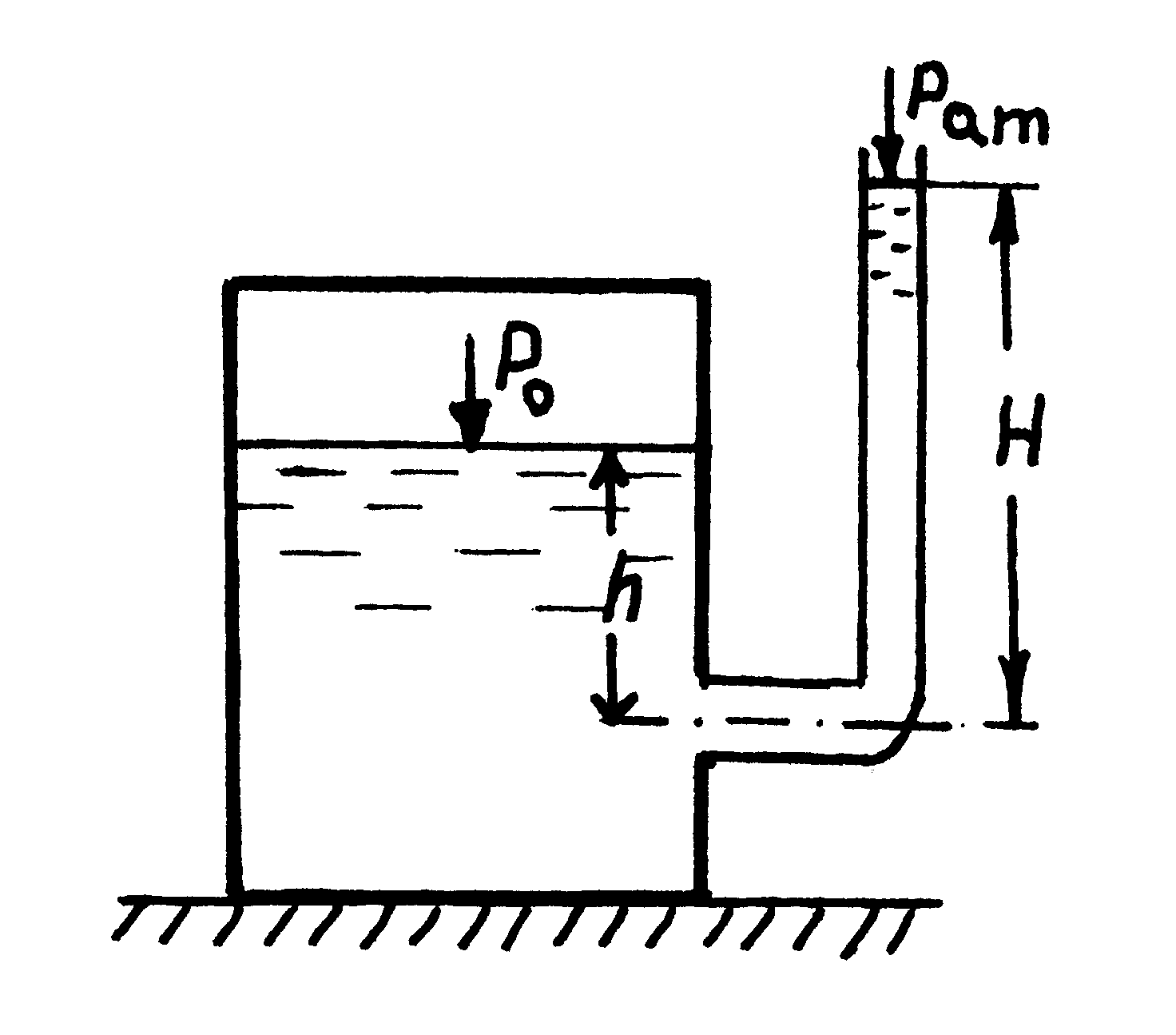



Рисунок 1

Тогда, обозначая через p_ат давление атмосферы, имеем:



где  - объемный вес воды;





Задача 1.2. Жидкостный вакуумметр. В сосуде А (рис. 2) часть воздуха выкачана и полное давление в нем p_А=0,08829 МПа. Сосуд соединен трубкой с водой резервуара В, находящейся под давлением атмосферы. Определить показания вакуумметра Н_вак.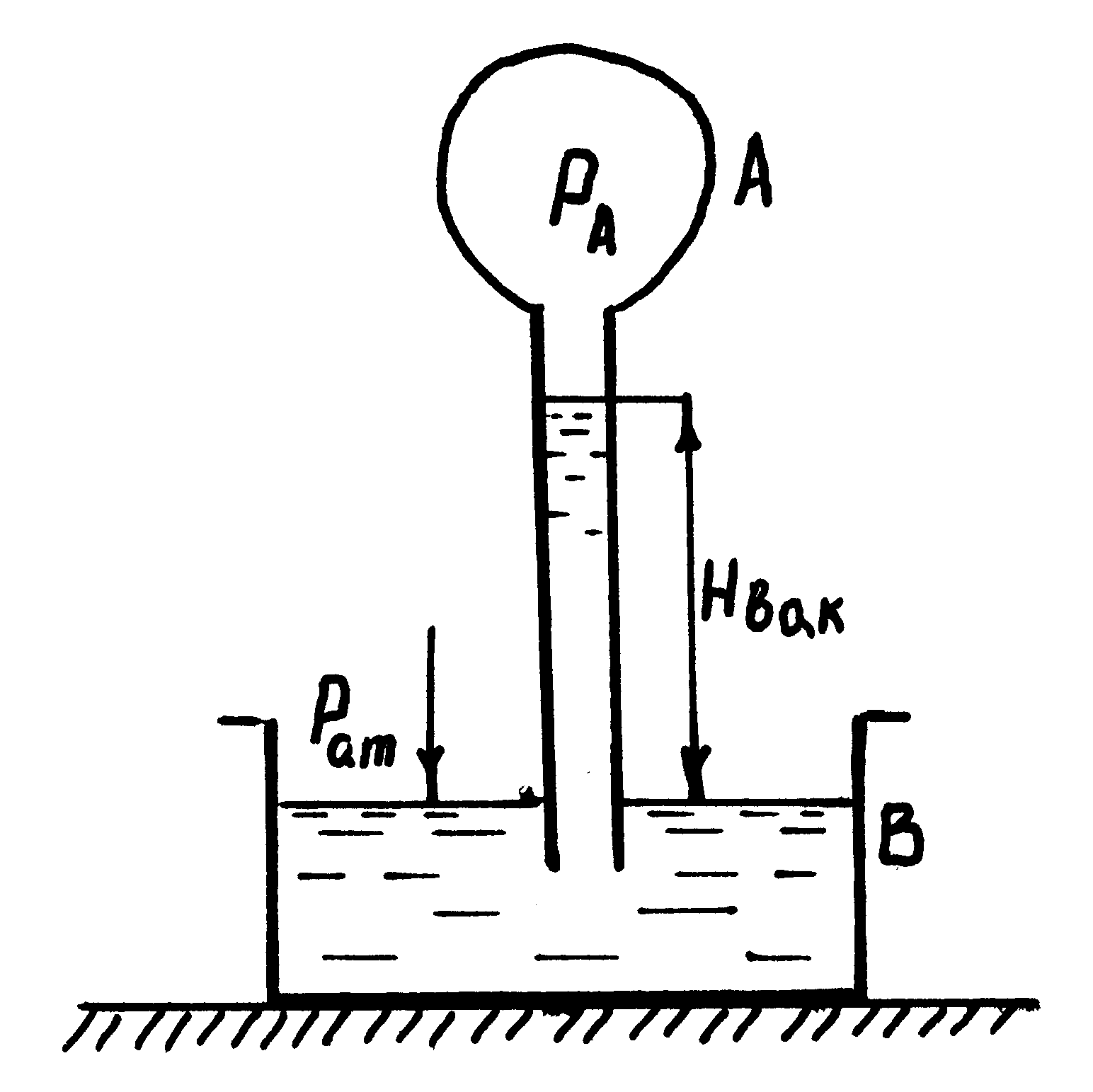



Рисунок 2

Решение.

Так как

то [5]





Задача 1.3. Боковая стенка АВСD открытого резервуара наклонена к горизонту под углом  = 60. Определить силу давления воды на трапецеидальную площадку, выделенную на боковой стенке. Размеры указанны на рисунке 3.



Рисунок 3­­

Решение. Определим глубину погружения центра тяжести интересующей нас площадки.

Центр тяжести трапеции находится от большего основания ее на расстоянии [2]



где В – большее основание трапеции;

b – меньшее основание трапеции;

L – высота трапеции.

Верхнее основание трапеции в данном случае находится на расстоянии е = 1 м от уреза воды, и потому положение центра тяжести, считая по наклону стенки, будет:





Глубина погружения центра тяжести от уровня воды





Площадь рассматриваемой трапеции





Искомое манометрическое давление на выделенную трапецеидальную площадку




Задача 1.4. Прямоугольный щит шириной b = 2 м соединен шарнирно по горизонтальной оси с дном сооружения, а вверху поддерживается крюками. Перед щитом глубина воды h₁ = 4 м, за ним h₂ = 2 м.



Рисунок 4

Определить реакцию шарнира R_ш и реакцию крюков R_к (рис. 4) от давления жидкости. Шарнир и крюки воспринимают на себя давление жидкости на щит слева P₁ и справа P₂.

Решение. Определим величину сил давления и точки их приложения с каждой стороны щита [2]:









считая от уровня жидкости, или 4 – 2,67 = 1,33 м от дна.

Соответственно имеем:









считая от уровня воды справа или 0,67 м от дна.

Давления на щит P₁ и P₂ направлены перпендикулярно плоскости щита в противоположные стороны, и щит находится под действием их равнодействующей P = P₁ – P₂ = 16 – 4 = 12 т, которую и должны принять на себя шарнир и крюки:

R_ш + R_к = 12 т.

Для расчета отдельно каждой реакции составим уравнение моментов сил.

Из уравнения моментов относительно шарнира



определим R_к = 4,14 т.

Из уравнения моментов относительно крюка



определим: R_ш = 7,86 т.

Проверяя, получаем:

R_ш + R_к = 4,14 + 7,86 = 12 т.

Задача 1.5. Определить, с какой силой Т необходимо тянуть трос, прикрепленный к нижней кромке прямоугольного затвора, размерами (21) м², закрывающего отверстие в плотине при данных на (рис. 5).

Решение. Определим давление P на затвор и точку его приложения:









Рисунок 5



от уровня воды, или 0,524 м от шарнира А.

Составим уравнение моментов сил относительно оси А [2]:





откуда

Т=5,19 т.

Задача 1.6. Из стали с допускаемым напряжением  = 147,15 МПа предполагают сделать трубу диамет­ром D = 1 м, в которой максимальное давление может достигать 500 м вод. ст. Рассчитать толщину стенок трубы.

Решение. Предположим, что ось трубы направлена верти­кально, и рассмотрим вырезанную из трубы полукруглую полосу шириной, равной единице (рис. 6).

Давление на поверхность рассматриваемой полу­круглой полосы будет, как уже известно, равно дав­лению на проекцию этой полосы, т. е. равно давлению на площадь диаметрального сечения:

Р = рDl. (19)

Это давление должно уравновешиваться силой со­противления стенок трубы рассматриваемой полосы.

Если обозначим сопротивление стенок трубы на рассматриваемом отрезке через Т, можно записать:



Это соотношение позволяет подсчитать толщину е тонкостенных труб, работающих под гидростатическим давлением р.



Рисунок 6

В самом деле, полагая силу Т равномерно распре­деленной по толщине е и обозначая через  допускае­мое напряжение в материале стенок, найдем так называемую формулу Мариотта [2]:



В условиях данного примера имеем р = 4,905 МПа и получим:



Задача 1.7. Отверстие водосбросного шлюза шириной b = 5 м закрывается сегментным щитом с радиусом r = 6 м. Ось вращения затвора находится на высоте 1 м над уровнем воды. Глубина воды перед щитом Н = 4 м; за щитом воды нет. Определить давление на затвор (рис. 7).

Решение. Найдем отдельно составляющие давления на за­твор. Горизонтальная составляющая давления будет [6]:



Рисунок 7





Для определения вертикальной составляющей най­дем соответствующий ей вес «тела давления» с попе­речным сечением, заштрихованным на (рис. 7).



Площадь AA"CD = площади треугольника АА"С + площадь сегмента ACD:











что соответствует  = 33°36';





что соответствует  = 9°36';

 +  = 43°12';

sin  = 90° – (+) = 46°48';

sin  = sin 46°48' = 0,729.

Подставляя полученные значения в уравнение (23), найдем площадь AA"CD = 6,77 м²;

G_ = P_z = 16,775 = 33,9 т.

Суммарное давление как равнодействующая обеих составляющих равно:





Эта сила пройдет через точку О.

Итак, на весь затвор передается давление 52,4 т.

Направление силы давления составляет с осью ОХ угол, характеризуемый величиной косинуса, равной



т. е. угол в 40°15'.

Задача 1.8. Определить центр давления на сегментный щит в задаче 1.7.

Решение. Так как элементарные силы нормальны к цилиндрической поверхности, то линия действия равнодействующей должна пройти через центр щита О. Поместив начало координат в точку О и приняв указанное на рисунке 8 направление осей координат, напишем уравнение прямой, проходящей через начало координат под углом  к оси ОХ:

z = tg  x . (28)

Точка пересечения этой прямой с окружностью x² + z² = r² и является центром давления.



Рисунок 8

В данном случае





и

r = 6 м;

тогда

z = 0,848 х;

х²+(0,848 х)² = 6²,

откуда



z = 0,848 * 4,59 =  3,88 м.

Согласно выбранной системе координат, центр давления должен находиться в третьем квадранте; следовательно,

х = - 4,59 м; z = - 3,88 м.

На рисунке 8 дано построение центра давления по центрам давления горизонтальной и вертикальной составляющих. Центр давления для горизонтальной составляющей можно определить по центру тяжести эпюры давления на проекцию щита.

Так как в данном случае линия действия равнодействующей сил давления должна пройти, кроме того, через центр окружности О, то мы имеем две точки: С и О, вполне определяющие положение искомой линии действия.