Сборник задач по практикам. Сборник задач по гидравлике может использоваться в качестве учебного пособия для практических занятий по курсу гидравлики и являться дополнением к лекционному курсу
 Скачать 1.79 Mb.
|
2 УРАВНЕНИЕ БЕРНУЛЛИ. СОПРОТИВЛЕНИЕ ДВИЖЕНИЮ ЖИДКОСТИЗадача 2.1. Пренебрегая потерями напора, определить диаметр горловины d2 (рис. 9), чтобы при пропуске расхода воды по трубопроводу Q = 0,0088 м3/с вода по трубке подсасывалась на высоту h = 55 см. Диаметр трубопровода d1 = 100 мм, а манометрическое давление в сечении 1-1 p1 = 0,003924 МПа ( 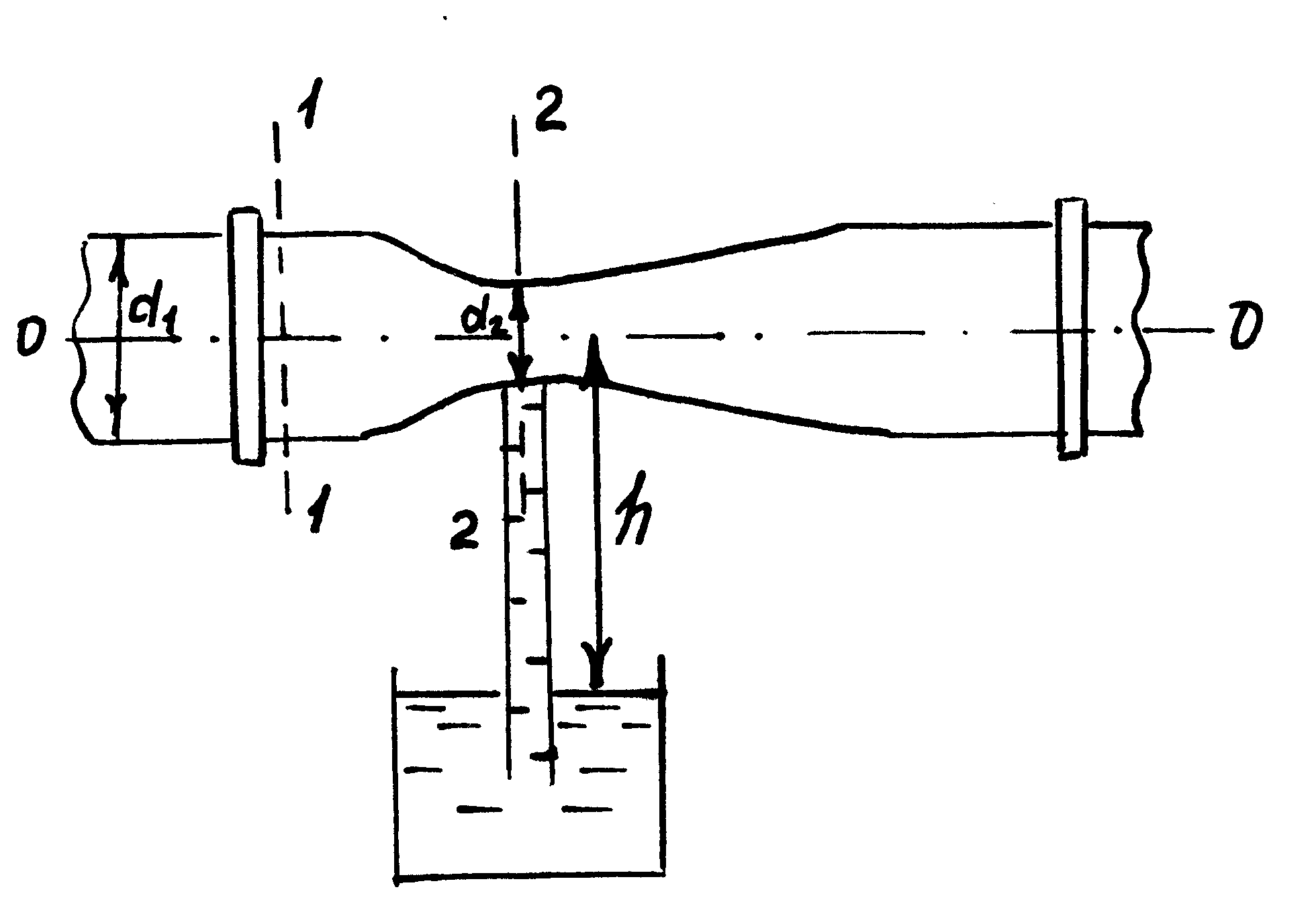 вод. ст.). Рисунок 9 Решение. Составам уравнение Бернулли для сечений 1-1 и 2-2,выбрав за плоскость сравнения ось трубы  Определим скоростной напор во втором сечении  где  - вакуум в сечении 2-2.Определим величину вакуума, обеспечивающего поднятие воды по трубке на высоту h = 55 см, составив условие равновесия  откуда  Вычислим площадь сечения трубопровода при d1 = 100 мм = 0,1 м   Скорость в первом сечении при Q = 0,0088 м3/с   Скоростной напор в первом сечении  Подставим числовые значения в уравнение Бернулли  тогда скорость во втором сечении  Определим диаметр горловины из уравнения для сечения (2-2)   Задача 2.2. Определить расход воды, вытекающей из трубы, и манометрическое давление в точке В (рис. 10). Уровень в резервуаре постоянный, глубина h = 5 м. Решение. Длина участков верхней трубы диаметром d1 = 150 мм равна  и  . Длина нижней трубы диаметром d2 = 100 мм  . Коэффициент Дарси вычислить по приближенной формуле (36). При расчете скоростным напором в резервуаре пренебречь. где d – диаметр, м. Составим уравнение Бернулли для двух сечений 1-1 и 2-2 относительно плоскости сравнения 0-0 (рис. 10).  или 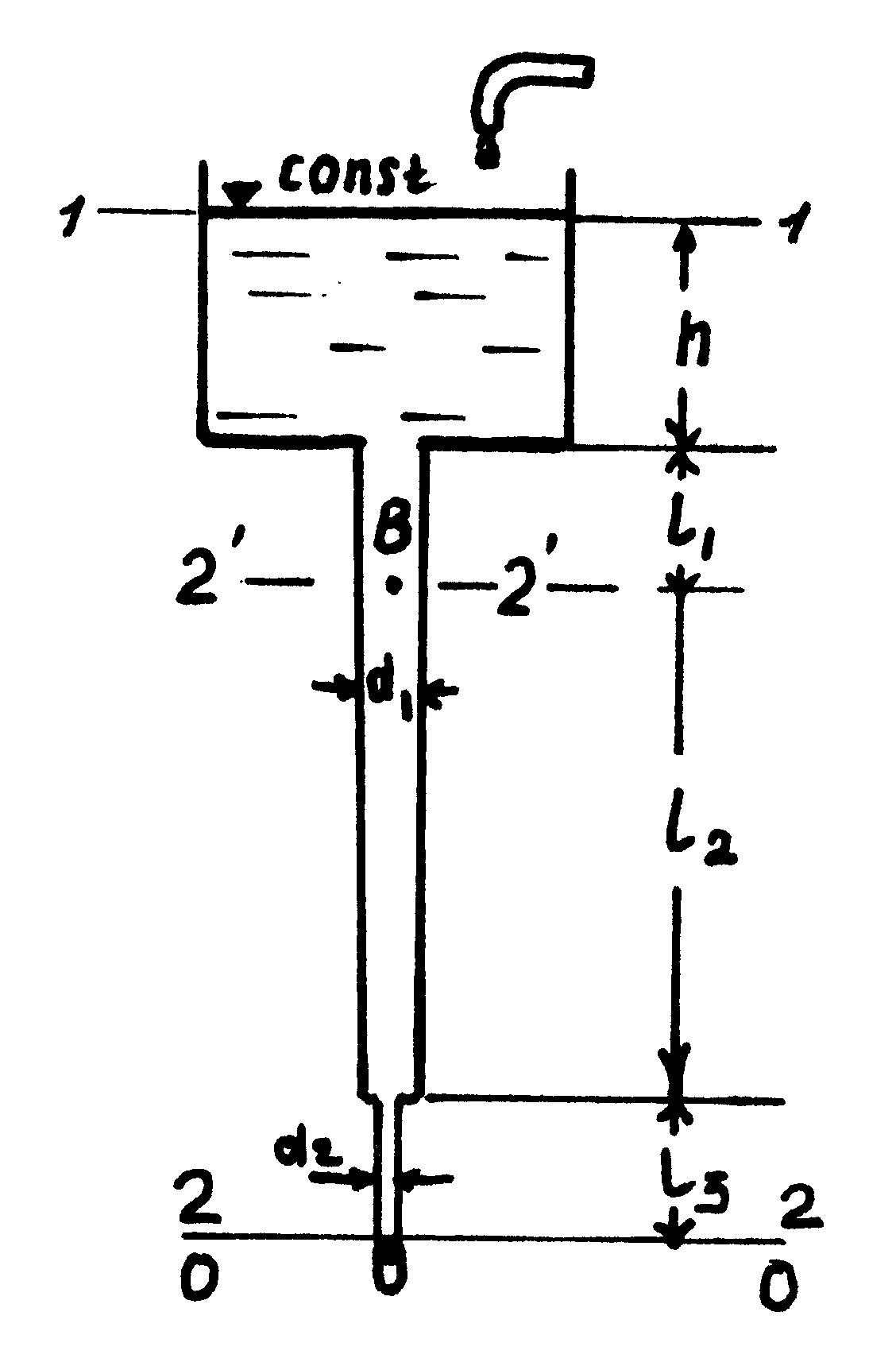  Рисунок 10 Определим потери напора  Выразим все потери через скорость 2, для чего найдем скорость 1 из уравнения неразрывности 11 = 22. Имеем:  Подставим найденное значение в уравнение, принимая коэффициенты местных сопротивлений и сопротивлений трения:   Подставим найденное значение в уравнение Бернулли  Скорость при выходе:   Расход Q = 22 = 0,00785*13 = 0,102 м3/c где  Для определения манометрического давления в трубе в точке Всоставим уравнение Бернулли для сечений 1-1 и 2'-2' относительно плоскости сравнения, проведенной через сечение 2'-2',  откуда   Задача 2.3. Канал трапецеидального сечения имеет следующие размеры: ширина по дну b = 3,8 м; коэффициент заложения откоса m = l,5; глубина воды h = 1,2 м. Определить режим движения в канале при пропуске расхода Q = 5,2м3/с. Температура воды t = 20°С. Решение. Для выяснения режима движения необходимо определить число Рейнольдса  где в качестве характерного геометрического размера русла принят гидравлический радиус R. Определим площадь живого сечения канала   Гидравлический радиус  где  – смоченный периметр, равный  тогда  Средняя скорость в канале   Кинематический коэффициент вязкости для воды при температуре 20° С равен  = 0,0101 см2/c.Тогда  Так как  то движение турбулентное.Задача 2.4. Определить потери напора при подаче воды со скоростью = 0,131 м/с, при температуре t = 10°C по трубопроводу диаметром d = 200 мм; длиной l= 1500 м. Трубы стальные новые. Решение. Задача может быть решена двумя способами. 1-й способ. Выясним режим движения, приняв коэффициент кинематической вязкости для воды при t = 10°С, = 0,0000131 м2/с Так как Re = 20000 > 2320, то режим движения турбулентный. Найдем число Рейнольдса, соответствующее границе гладкой зоны  Для новых стальных труб высота шероховатости  0,45 мм. Принимая  = 0,45 мм, вычислим: Так как число Re = 20000 < 28667, то рассматриваемый случай относится к области гладких труб. Вычисляем по формуле   Потери напора   2-й способ. Выясняем режим движения, так же как и в 1-м случае. Так как полученное число Рейнольдса является сравнительно небольшим Re = 20000, то предполагаем, что трубы работают как гидравлически гладкие, и находим по формуле Кольбрука. При Re = 20000 = 0,0257. Определяем по формуле толщину ламинарного слоя у стенок трубы   Так как ламинарный слой у стенок пл = 1,86 мм > = 0,45 мм,то наше предположение правильное – трубы будут работать как гидравлически гладкие. Следовательно, значение для найдено правильно ( = 0,0257). Напор определим по формуле   Задача 2.5. Определить потери напора в водопроводе длиной = 500 м при подаче Q = 0,1 м3/с, если трубы чугунные, бывшие в эксплуатации с d = 250 мм и = 1,35 мм. Температура воды t = 10° С. Решение. Выясним режим движения, принимая кинематический коэффициент вязкости для воды при t = 10° С = 0,0131 см2/с   где – скорость в трубе, равная   Так как Re = 389313 > 2320, то режим движения турбулентный. Число Рейнольдса получилось сравнительно большим, поэтому предполагаем, что движение происходит в квадратичной области сопротивления. Находим по формуле число Рейнольдса, при превышении которого начинается квадратичная область  где С – скоростной множитель, который может быть найден, например по формуле Агроскина [1]: С = 17,72 (n + lg R) = 17,72 (4,04 + lg 0,0625) = 17,72 (4,04 - 1,204) = 50,2 м0,5/с, где параметр гладкости принят n = 4,04 для чугунных труб, бывших в эксплуатации, а гидравлический радиус  Подставляя найденное значение для С, получаем:  Так как Re = 389313 >  = 201000, то движение происходит в квадратичной области и наше предположение было правильным.Определим потери напора по формуле   |