Сборник СОР и СОЧ 7 класс рус. Сборник заданий для

• Название: Сборник заданий для
• Дата: 09.03.2023
• Размер: 0.83 Mb.
• Имя файла: Сборник СОР и СОЧ 7 класс рус.docx
• Тип: Сборник; #977335
• страница: 20 из 43

ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА РАЗДЕЛЫ 2 ЧЕТВЕРТИ

Суммативное оценивание за раздел «Треугольники» Цель обучения:

7.1.1.12 знать определение медианы, биссектрисы, высоты, серединного перпендикуляра и средней линии треугольника и изображать их

21. 
    знать и доказывать признаки равенства треугольников
    
22. 
    применять признаки равенства треугольников при решении задач на вычисление и на доказательство
    
23. 
    применять свойства и признаки равнобедренного треугольника.
    

Критерий оценивания:

Обучающийся

• 
  Определяет медиану, биссектрису, высоту треугольника по чертежу
  
• 
  Распознает равные элементы фигур и определяет соответствующий признак равенства треугольников
  
• 
  Использует свойства равнобедренного треугольника для решения задач
  
• 
  Применяет признаки равенства треугольников при решении задач на доказательство.
  

Уровень мыслительных навыков: Применение Навыки высокого порядка

Время выполнения 25 минут

Вариант 1
Задание 1. На рисунке изображены треугольники. Укажите названия следующих элементов на рисунке (медиана, биссектриса, высота).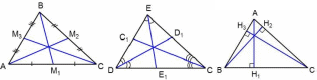



АМ₂ - ЕЕ₁ - ВН₂ -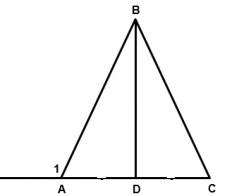
Задание 2. Луч AК – биссектриса угла ВАС. На сторонах угла отложены равные отрезки АВ и АС. Запишите равные элементы треугольников ВАК и САК и определите, по какому признаку треугольники равны.
Задание 3. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса BD. Найдите градусные меры углов BDC и BCA, если и 1  115⁰ .

Задание 4. Треугольник DОВ – равнобедренный, ВD – основание, MDB  KBD . Докажите, что ВМ=DК.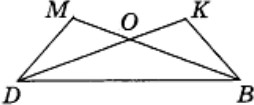

Вариант 2

Задание 1. На рисунке изображены треугольники. Укажите названия следующих элементов на рисунке (медиана, биссектриса, высота).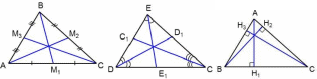



ВМ₁ - СС₁ - СН₃-

Задание 2. Луч AЕ – биссектриса угла ВАС. На сторонах угла отложены равные отрезки АВ и АС. Запишите равные элементы треугольников ВАЕ и САЕ и определите, по какому признаку треугольники равны.
Задание 3. В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. Найдите градусные меры углов BDC и BCA, если и 1  140⁰ .


Задание 4. Треугольник DОВ – равнобедренный, ВD – основание, MDB  KBD . Докажите, что DМВ =DКВ.