Различные методы умножения. различные методы умножения. Счёт и вычисления основа порядка в голове
 Скачать 0.57 Mb.
|
Фотоблоги
степени из многозначного числа), добился таких потрясающих успехов в счёте в результате многолетней тренировки. Итак, многие «счётчики-феномены» пользуются особыми приемами быстрого счёта и специальными формулами. Значит, мы тоже можем пользоваться некоторыми из этих приёмов. ГлаваII. Старинные способы умножения. 2.1. Русский крестьянский способ умножения. В России 2-3 века назад среди крестьян некоторых губерний был распространен способ, который не требовал знание всей таблицы умножения. Надо было лишь уметь умножать и делить на 2. Этот способ получил название крестьянского(существует мнение, что он берет начало от египетского). Пример: умножим 47 на 35, - запишем числа на одной строчке, проведём между ними вертикальную черту; - левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем); - деление заканчивается, когда слева появится единица; - вычёркиваем те строчки, в которых стоят слева чётные числа; - далее оставшиеся справа числа складываем – это результат; 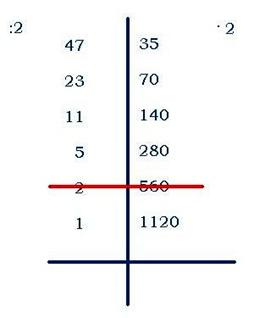 35 + 70 + 140 + 280 + 1120 = 1645.2.2. Метод «решетки». 1). Выдающийся арабский математик и астроном Абу Абдалах Мухаммед Бен Мусса аль - Хорезми жил и работал в Багдаде. «Аль - Хорезми» буквально означает «из Хорезми», т. е. родился в г. Хорезме (сейчас входит в состав Узбекистана). Учёный работал в Доме мудрости, где были библиотека и обсерватория, здесь работали почти все крупные арабские учёные. Сведений о жизни и деятельности Мухаммеда аль - Хорезми очень мало. Сохранились лишь две его работы – по алгебре и по арифметике. В последний из этих книг даны четыре правила арифметических действий, почти такие же, что используются в наше время. 2). В своей «Книге об индийском счете» учёный описал способ, придуманный в Древней Индии, а позже названный«методом решётки» (он же «ревность»). Этот метод даже проще, чем применяемый сегодня. Пусть нужно умножить 25 и 63. 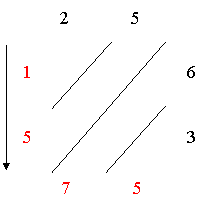 Начертим таблицу в которой две клетки по длине и две по ширине запишем одно число по длине другое по ширине. В клетках запишем результат умножения данных цифр, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали, и полученный результат можно прочитать по стрелке (вниз и вправо).
 Нами рассмотрен простой пример, однако, этим способом можно умножать любые многозначные числа. Рассмотрим еще один пример: перемножим 987 и 12: - рисуем прямоугольник 3 на 2 (по количеству десятичных знаков у каждого множителя); - затем квадратные клетки делим по диагонали; - вверху таблицы записываем число 987; - слева таблицы число 12 (см. рисунок); - теперь в каждый квадратик впишем произведение цифр – сомножителей, расположенных в одной строчке и в одном столбце с этим квадратиком, десятки выше диагонали, единицы ниже; - после заполнения всех треугольников, цифры в них складывают вдоль каждой диагонали; - результат записываем справа и внизу таблицы (см. рисунок); 987 ∙ 12=11844 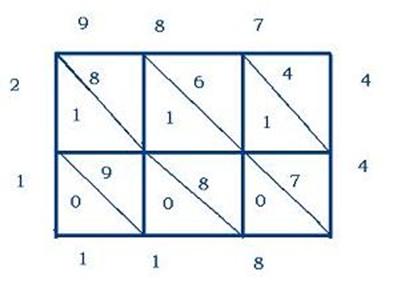 Этот алгоритмом умножения двух натуральных чисел был распространен в средние века на Востоке и Италии. Неудобство этого способа мы отметили в трудоемкости подготовки прямоугольной таблицы, хотя сам процесс вычисления интересен и заполнение таблицы напоминает игру. 2.3 Индийский способ умножения Некоторые опытные учителя в прошлом веке считали, что этот способ должен заменить в нашей школе общепринятый способ умножения. Американцам он настолько понравился, что они его даже так и назвали «Американский способ». Однако им пользовались жители Индии еще в VI в. н. э., и правильнее его назвать «индийским способом». Перемножить два каких - либо двузначных числа, скажем 23 на 12. Я сразу пишу, что получится. х23 12 276 Вы видите: очень быстро получен ответ. Но как он получен? Первый шаг: х23 говорю: «2 х 3 = 6» 12 …6 Второй шаг: х23 говорю: « 2 х 2 + 1 х 3 = 7» 12 .76 Третий шаг: х23 говорю: «1 х 2 = 2». 12 пишу 2 левее цифры 7 276 получаем 276. Мы познакомились с этим способом на очень простом примере без перехода через разряд. Однако наши исследования показали, что им можно пользоваться и при умножении чисел с переходом через разряд, а также при умножении многозначных чисел. Приведем примеры: х528 х24 х15 х18 х317 123 30 13 19 12 643804 На Руси этот способ был известен как способ умножения крестиком. В этом «крестике» и заключается неудобство умножения, легко запутаться, к тому же трудно удерживать в уме все промежуточные произведения, результаты которых затем надо сложить. 2.4. Египетский способ умножения Обозначения чисел, которые использовались в древности, были более или менее пригодны для записи результата счета. А вот выполнять арифметические действия с их помощью было очень сложно, особенно это касалось действия умножения (попробуй, перемножь: ξφß*τδ).  Выход из этой ситуации нашли египтяне, поэтому способ получил название египетского.Они заменили умножение на любое число - удвоением, то есть сложением числа с самим собой.
Пример: 34 ∙ 5=34∙ (1 + 4) = 34∙ (1 + 2 ∙ 2) = 34 ∙ 1+ 34 ∙ 4. Т. к. 5 = 4 + 1, то для получения ответа оставалось сложить числа, стоящие в правом столбике против цифр 4 и 1 , т. е. 136 + 34 = 170.  2.5. Умножение на пальцах Древние египтяне были очень религиозны и считали, что душу умершего в загробном мире подвергают экзамену по счёту на пальцах. Уже это говорит о том значении, которое придавали древние этому способу выполнения умножения натуральных чисел (он получил название пальцевого счета). Умножали на пальцах однозначные числа от 6 до 9. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходил число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. После этого брали столько десятков, сколько вытянуто пальцев на обеих руках, и прибавляли к этому числу произведение загнутых пальцев на первой и второй руке. П 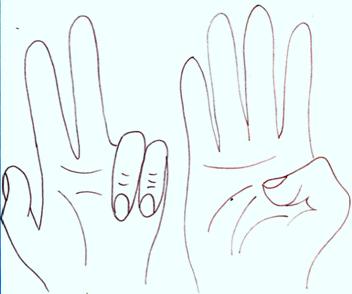 ример: 8 ∙ 9 = 72Позже пальцевой счёт усовершенствовали – научились показывать с помощь пальцев числа до 10000 Движение пальца А 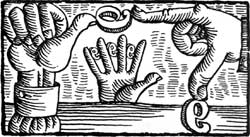 вот еще один из способов помочь памяти: с помощью пальцев рук запомнить таблицу умножения на 9. Положив обе руки рядом на стол, по порядку занумеруем пальцы обеих рук следующим образом: первый палец слева обозначим 1, второй за ним обозначим цифрой 2, затем 3, 4… до десятого пальца, который означает 10. Если надо умножить на 9 любое из первых девяти чисел, то для этого, не двигая рук со стола, надо приподнять вверх тот палец, номер которого означает число, на которое умножается девять; тогда число пальцев, лежащих налево от поднятого пальца, определяет число десятков, а число пальцев, лежащих справа от поднятого пальца, обозначает число единиц полученного произведения.Пример. Пусть надо найти произведение 4х9. Положив обе руки на стол, приподнимем четвертый палец, считая слева направо. Тогда до поднятого пальца находятся три пальца (десятки), а после поднятого - 6 пальцев (единицы). Результат произведения 4 на 9, значит, равен 36. Еще пример: Пусть требуется умножить 3 * 9. Слева направо найдите третий палец, того пальца выпрямленными будут 2 пальца, они и будут означать 2 десятка. Справа от загнутого пальца выпрямленными окажутся 7 пальцев, они означают 7 единиц. Сложите, 2 десятка и 7 единиц получится 27. Сами пальцы показали это число. // // ///// 20 7 Итак, рассмотренные нами старинные способы умножения показывают, что используемый в школе алгоритм умножения натуральных чисел - не единственный и известен он был не всегда. Однако, он достаточно быстр и наиболее удобен. Глава 3. Устный счет – гимнастика ума 3.1. Умножение и деление на 4. Чтобы умножить число на 4, его дважды удваивают. Например, 214 * 4 = (214 * 2) * 2 = 428 * 2 = 856 537 * 4 = (537 * 2) * 2 = 1074 * 2 = 2148 Чтобы число разделить на 4 , его дважды делят на 2. Например, 124 : 4 = (124 : 2) : 2 = 62 : 2 = 31 2648 : 4 = (2648 : 2) : 2 = 1324 : 2 = 662 3.2. Умножение и деление на 5. Чтобы умножить число на 5, нужно его умножить на 10/2 , то есть умножить на 10 и разделить на 2. Например, 138 * 5 = (138 * 10) : 2 = 1380 : 2 = 690 548 * 5 (548 * 10) : 2 = 5480 : 2 = 2740 Чтобы число разделить на 5, нужно умножить его на 0,2, то есть в удвоенном исходном числе отделить запятой последнюю цифру. Например, 345 : 5 = 345 * 0,2 = 69,0 51 : 5 = 51 * 0,2 = 10,2 3.3. Умножение на 25. Чтобы умножить число на 25, нужно его умножить на 100/4, то есть умножить на 100 и разделить на 4. Например, 348 * 25 = (348 * 100) : 4 = (34800 : 2) : 2 = 17400 : 2 = 8700 3.4. Умножение на 1,5. Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину. Например, 26 * 1,5 = 26 + 13 = 39 228 * 1,5 = 228 + 114 = 342 127 * 1,5 = 127 + 63,5 = 190,5 3.5. Умножение на 9. Чтобы умножить число на 9, к нему приписывают 0 и отнимают исходное число. Например, 241 * 9 = 2410 – 241 = 2169 847 * 9 = 8470 – 847 = 7623 3.6. Умножение на 11. 1 способ. Чтобы число умножить на 11, к нему приписывают 0 и прибавляют исходное число. Например: 47 * 11 = 470 + 47 = 517 243 * 11 = 2430 + 243 = 2673 2 способ. Если хочешь умножить число на 11, то поступай так: запиши число, которое нужно умножить на 11, а между цифрами исходного числа вставь сумму этих цифр. Если сумма получается двузначное число, то 1 прибавляем к первой цифре исходного числа. Например:     45 * 11 = * 11 = 9674 (4+5+7) 7 Такой способ подходит только для умножения двузначных чисел. 3.7. Умножение трехзначного числа на 101. Например 125 * 101 = 12625 (увеличиваем первый множитель на число его сотен и приписываем к нему справа две последние цифры первого множителя) 125 + 1 = 126 12625 Этот прием дети легко усваивают при записи вычисления в столбик
Еще пример: 527 * 101 = (527+5)27 = 53227
3.8. Возведение в квадрат числа, оканчивающегося цифрой 5. Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 65), умножают число его десятков (6) на число десятков, увеличенное на 1 (на 6+1 = 7), и к полученному числу приписывают 25 (6 * 7 = 42 Ответ: 4225) Например:  952 = 90259 *10  1252 = 1562512 * 13 3.8. Возведение в квадрат числа, близкого к 50. Если хочешь возвести в квадрат число, близкое к 50, но большее 50, то поступай так: 1) вычти из этого числа 25; 2) припиши к результату двумя цифрами квадрат избытка данного числа над 50. Примеры: 1) 582 = 3364. Объяснение: 58 – 25 = 33, 82 = 64, 582 = 3364. 2) 672 = 4489 Объяснение: 67 – 25 = 42, 67 – 50 = 17, 172 =289, 672 = 4200 + 289 = 4489. Если хочешь возвести в квадрат число, близкое к 50, но меньшее 50, то поступай так: 1) вычти из этого числа 25; 2) припиши к результату двумя цифрами квадрат недостатка данного числа до 50. Примеры: 1) 482 = 2304. Объяснение: 48 – 25 = 23, 50 – 48 =2, 22 = 4, 482 = 2304. 2) 372 = 1369 Объяснение: 37 – 25 = 12,= 13, 132 =169, 372 = 1200 + 169 = 1369. 3.9. Игры Отгадывание полученного числа. 1. Задумайте какое-нибудь число. Прибавьте к нему 11; умножьте полученную сумму на 2; от этого произведения отнимите 20; умножьте полученную разность на 5 и от нового произведения отнимите число, в 10 раз больше задуманного вами числа. Я отгадываю: вы получили 10. Верно? 2. Задумайте число. Утрой его. Вычти из полученного 1. Полученное умножьте на 5. К полученному прибавьте 20. Разделите полученное на 15. Из полученного вычтите задуманное. У вас получилось 1. 3. Задумайте число. Умножьте его на 6. Вычтите 3. Умножьте на 2. Прибавьте 26. Вычтите удвоенное задуманное. Разделите на 10. Вычтите задуманное. У вас получилось 2. 4. Задумайте число. Утройте его. Вычтите 2. Умножьте на 5. Прибавьте 5. Разделите на 5. Прибавьте 1. Разделите на задуманное. У вас получилось 3. 5. Задумайте число, удвойте его. Прибавьте 3. Умножьте на 4. Вычтите 12. Разделите на задуманное. У вас получилось 8. Угадывание задуманных чисел. Предложите своим товарищам задумать любые числа. Пусть каждый прибавит к своему задуманному числу 5. Полученную сумму пусть умножит на 3. От произведения пусть отнимет 7. Из полученного результата пусть вычтет ещё 8. Листок с окончательным результатом пусть каждый отдаст вам. Глядя на листок, вы тут же говорите каждому, какое число он задумал. (Чтобы угадать задуманное число, результат, написанный на бумажке или сказанный вам устно, разделить на 3) Заключение Мы вступили в новое тысячелетие! Грандиозные открытия и достижения человечества. Мы много знаем, многое умеем. Кажется чем-то сверхъестественным, что с помощью чисел и формул можно рассчитать полёт космического корабля, «экономическую - ситуацию» в стране, погоду на «завтра», описать звучание нот в мелодии. Нам известно высказывание древнегреческого математика, философа, жившего в 4 веке д. н.э.- Пифагора - «Всё есть число!». Согласно философскому воззрению этого учёного и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса. Описывая старинные способы вычислений и современные приёмы быстрого счёта, мы попытались показать, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись. Изучение старинных способов умножения показало, что это арифметическое действие было трудным и сложным из-за многообразия способов и их громоздкости выполнения. Современный способ умножения прост и доступен всем. При знакомстве с научной литературой обнаружили более быстрые и надежные способы умножения. Поэтому изучение действия умножения – тема перспективная. Возможно, что с первого раза у многих не получится быстро, с ходу выполнять эти или другие подсчеты. Пусть сначала не получится использовать прием, показанный в работе. Не беда. Нужна постоянная вычислительная тренировка. Из урока в урок, из года в год. Она поможет приобрести полезные навыки устного счета. Список использованной литературы 1. Ванцян А. Г. Математика: Учебник для 5 класса. - Самара: Издательский дом «Фёдоров», 1999. 2. Кордемский Б. А., Ахадов А. А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986. 3. Минских Е. М. «От игры к знаниям», М., «Просвещение» 1982г. 4. Свечников А. А. Числа, фигуры, задачи М., Просвещение, 1977г. 5. http://matsievsky. *****/sys-schi/file15.htm 6. http://*****/mod/1/6506/hystory. html |
