100 баллдық вышмат. Сені олынан брі келеді, тек зіе сен (кейбір сратарды жауабын таба алмадым, барымша істедім) жне матрицалары берілген
 Скачать 2.04 Mb. Скачать 2.04 Mb.
|
|
+белгісіз функция 186. Бернулли әдісінде 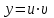 алмастыруда v функциясы алмастыруда v функциясы+сәйкес біртекті теңдеудің дербес шешімі 187. 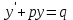 дифференциалдық теңдеудің дифференциалдық теңдеудің 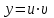 алмастыруда v функциясының шешімі алмастыруда v функциясының шешімі+ 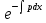 188. 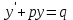 дифференциалдық теңдеудің дифференциалдық теңдеудің 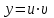 алмастыруда u функциясының шешімі алмастыруда u функциясының шешімі+ 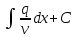 189. 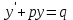 дифференциалдық теңдеудің Лагранж әдісінің басқа атауы дифференциалдық теңдеудің Лагранж әдісінің басқа атауы+тұрақтыларды варияциялау 190. 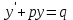 дифференциалдық теңдеудің p, q ______ функциялар дифференциалдық теңдеудің p, q ______ функциялар+x-қа тәуелдi функциялар немесе тұрақты шамалар +біртекті 191. Сызықтыбіртектідифференциалдықтеңдеу *+ 192. Сызықты біртекті емес дифференциалдық теңдеу *+ + 193. Сызықтық дифференциалдық теңдеу +у'-2у/х=2х 194. Берілген дифференциалдық теңдеулердің қайсысы бірінші ретті сызықтық теңдеу болады *+ 195. Бірінші ретті сызықтық дифференциалдық теңдеу:*+ 195. y-yctgx=2xsinx теңдеуді шешіңіз:*+y=(x2+С)sinx 196. 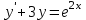 теңдеуінің p(x), q(x)-?+ p(x)=3, q(x)= e2x теңдеуінің p(x), q(x)-?+ p(x)=3, q(x)= e2x197. xdx+ydy=0 теңдеудi шешіңіз: -х +  198. 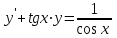 теңдеудi шешіңіз теңдеудi шешіңіз+y=sinx+C*cosx 199. 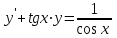 теңдеуінің p(x), q(x)-? теңдеуінің p(x), q(x)-?P(x)=tgx q(x)= 1/cosx 200. 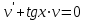 теңдеудi шешіңіз теңдеудi шешіңіз+y=C*cosx 201. у'-2у/х=х2 теңдеудi шешіңіз +y= x^2(C+x) 202. у'-2у/х=2хтеңдеуінің p(x), q(x)-? +p(x)=-2/х,q(x)= 2х 203. у'-2у/х=0 теңдеудi шешіңіз +y=х2C 204. у'+у/х=хтеңдеуінің p(x), q(x)-? + p(x)= 1/х, q(x)=x 205. 2-ші ретті дифференциалдық теңдеу + 206. 3-ші ретті дифференциалдық теңдеу *+ 207. 2-ші ретті дифференциалдық теңдеу *+ 208. 209. 210. 211. 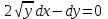 дифференциалдық теңдеудің шешу әдісі: +айнымалыны алмастыру әдіс дифференциалдық теңдеудің шешу әдісі: +айнымалыны алмастыру әдіс212. Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады... + 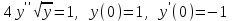 213. 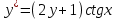 дифференциалдық теңдеуді дифференциалдық теңдеуді 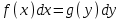 түріне келтір түріне келтір+ctgx*dx=dy/2y+1 214. 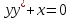 дифференциалдық теңдеуді дифференциалдық теңдеуді 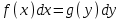 түріне келтір:-x*dx=ydy түріне келтір:-x*dx=ydy215. 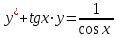 сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек p(x)=tgx g(x)=1/cosx 216.  сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек: p(x)=-4/х g(x)=х сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек: p(x)=-4/х g(x)=х217.  сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек : p(x)=1/x g(x)=3x сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек : p(x)=1/x g(x)=3x218. Дифференциалдық теңдеудің жалпы шешімі  және бастапқы шартты және бастапқы шартты  белгілі болса, онда С неге тең белгілі болса, онда С неге тең С=-2 219. Дифференциалдық теңдеудің жалпы шешімі  және бастапқы шартты және бастапқы шартты  белгілі болса, онда С неге тең: С=1 белгілі болса, онда С неге тең: С=1220. Дифференциалдық теңдеудің реті *+туындының жоғарғы ретін 221. Дифференциалдық теңдеудің орнына қойғанда оны теңбе-теңдікке айналдыратын кез-келген функция...: *+дифференциалдық теңдеудің шешімі 222. Бірінші ретті дифференциалдық теңдеудің жалпы шешімі *+  223. Коши есебі: *+ тәуелсіз айнымалының бастапқы берілуі 224. *+айнымалылары ажыратылатын дифференциалдық теңдеу 225.  - олардың туындылары: n-ші ретті дифференциалдық теңдеу - олардың туындылары: n-ші ретті дифференциалдық теңдеу226. n-ші ретті дифференциалдық теңдеу: + 227.  дифференциалдық теңдеудің шешу әдісі дифференциалдық теңдеудің шешу әдісі +Айнымалыны ажырату 228. Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады... +y’+(x+1)y=x  , x(3)=1, y(0)=1 , x(3)=1, y(0)=1229.  дифференциалдық теңдеуді дифференциалдық теңдеуді  түріне келтір түріне келтір2sinx*dx=dy/y 230.  сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек 231. Дифференциалдық теңдеудің жалпы шешімі  және бастапқы шартты және бастапқы шартты  белгілі болса, онда С неге тең белгілі болса, онда С неге тең C=-2 232.  дифференциалдық теңдеудің шешу әдісі дифференциалдық теңдеудің шешу әдісі+айнымалыны ажырату 233.  дифференциалдық теңдеуді дифференциалдық теңдеуді  түріне келтір түріне келтірSinxdx=dy/5y-1 234.  дифференциалдық теңдеуінің реті дифференциалдық теңдеуінің реті+3 235. xdy=ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=1, y=4 болса Y=4x #32  дифференциалдық теңдеуінің шешімі: дифференциалдық теңдеуінің шешімі:#33  дифференциалдық теңдеуінің шешімі: дифференциалдық теңдеуінің шешімі:#34xdy=ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=2, y=4 болса Ответ: 2 #35Решение уравнения  , если х=1 , y=1с= 1 , y(x)=cx^5 , если х=1 , y=1с= 1 , y(x)=cx^5#37  болғандағы, болғандағы,  дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: Ответ: 4 дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: Ответ: 4#38 Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады... #39 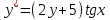 дифференциалдық теңдеуді дифференциалдық теңдеуді 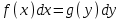 түріне келтір түріне келтір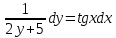 #40 Дифференциалдық теңдеудің жалпы шешімі 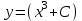 және бастапқы шартты және бастапқы шартты 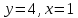 белгілі болса, онда С неге тең Ответ: 3 белгілі болса, онда С неге тең Ответ: 3#1 Алғашқы функцияның дифференциалынан алынған анықталмаған интеграл неге тең 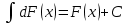 #2 Егер С – тұрақтысанболса, онда 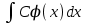 интегралы тең: интегралы тең: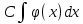 #3 *!Функцияның алгебралық қосындысының анықталмаған интегралы 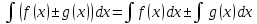 #4Егер F(x) функциясының туындысы f(x)-ке тең болса, онда F(x).....деп аталады: алғашқы функция #5 Анықталмаған интегралдың дифференциалы тең:интеграл таңбасының астындағы функцияға #6Егер F(x) функциясы f(x) үшін алғашкы функция болса, онда F(x)+c өрнегі ... деп аталады анықталмаған интеграл. #7 Функцияның анықталмаған интегралын есептеу процесi:интегралдау #8 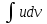 =*= =*=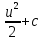 или или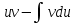 8. 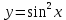 функциясының туындысы неге тең: sin2x функциясының туындысы неге тең: sin2x#9 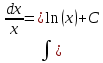 #10 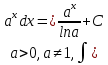 #11 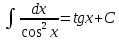 #12 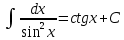 #13 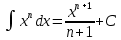 #14 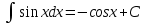 #1*! 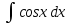 интегралы үшін интегралдау әдісі:Тікелей интегралдау интегралы үшін интегралдау әдісі:Тікелей интегралдау#2*!n-нiң қандай мәнiнде 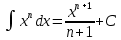 орындалмайды n=-1. орындалмайды n=-1.#3*!Анықталмаған интеграл үшін бөліктеп интегралдау формуласы: 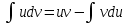 #4*! 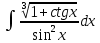 интегралы үшін интегралдау әдісі Жаңа айн интегралы үшін интегралдау әдісі Жаңа айн#5*! 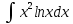 интегралындағы u=ln(x) және dv=x^2 интегралындағы u=ln(x) және dv=x^2#6*! 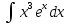 интегралындағы u=x^3 және dv=e^x интегралындағы u=x^3 және dv=e^x#7*! #8*!Тікелей интегралдау әдісімен есептелетін интеграл 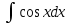 #9*! 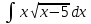 интегралы үшін интегралдау әдісі Жаңа айн интегралы үшін интегралдау әдісі Жаңа айн#10*! 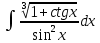 интегралы үшін интегралдау әдісі Жаңа айн интегралы үшін интегралдау әдісі Жаңа айн#11*! 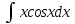 интегралы үшін интегралдау әдісі: Бөліктеп интегралдау интегралы үшін интегралдау әдісі: Бөліктеп интегралдау#14*! 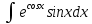 алмастыру Жаңа айн алмастыру Жаңа айн#1 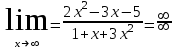 Берілген анықталмағандықты ашу әдісі: алымын да, бөлімін де х-тің ең үлкен дәрежесіне бөлу Берілген анықталмағандықты ашу әдісі: алымын да, бөлімін де х-тің ең үлкен дәрежесіне бөлу#2 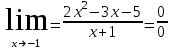 . Берілген анықталмағандықты ашу әдісі:көпмүшені көбейткіштерге жіктеу . Берілген анықталмағандықты ашу әдісі:көпмүшені көбейткіштерге жіктеу#3 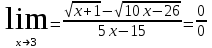 . Берілген анықталмағандықты ашу әдісі: Алымын және бөлімін түйіндес өрнекке көбейту . Берілген анықталмағандықты ашу әдісі: Алымын және бөлімін түйіндес өрнекке көбейту#4 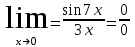 . Берілген анықталмағандықты ашу әдісі: Тамаша шекке келтіру . Берілген анықталмағандықты ашу әдісі: Тамаша шекке келтіру#5 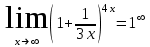 . Берілген анықталмағандықты ашу әдісі: Тамаша шекке келтіру . Берілген анықталмағандықты ашу әдісі: Тамаша шекке келтіру#6 Егер 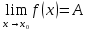 және және 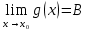 , онда , онда 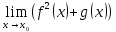 шегі тең: *+ шегі тең: *+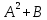 #7 Егер 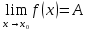 және және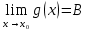 , онда , онда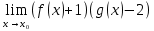 шегі тең*+(А+1)(В-2) шегі тең*+(А+1)(В-2)#8Егер 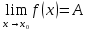 және және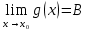 , онда , онда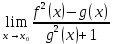 шегі тең *+ шегі тең *+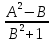 #9 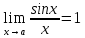 теңдігі дұрыс болатындай а мәнін табыңдар:*+ теңдігі дұрыс болатындай а мәнін табыңдар:*+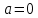 #10 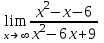 шектің мәні: 1 шектің мәні: 1#11 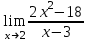 шектің мәні:10 шектің мәні:10#12 Егер 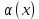 функциясы функциясы 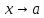 болғанда шексіз аз шама болса, онда f(x)= болғанда шексіз аз шама болса, онда f(x)=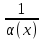 функциясы:*+ функциясы:*+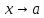 болғанда шексіз үлкен шама болғанда шексіз үлкен шама #13 Егер 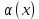 функциясы функциясы 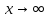 болғанда шексіз үлкен шама болса, онда f(x)= болғанда шексіз үлкен шама болса, онда f(x)=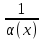 функциясы*+ x→a болғанда шексіз аз шама функциясы*+ x→a болғанда шексіз аз шама#14 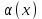 функциясы функциясы 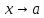 болғанда шексіз үлкен шама деп аталады, егер:limα(x)=∞ болғанда шексіз үлкен шама деп аталады, егер:limα(x)=∞#1 Бірінші тамаша шек:*+ 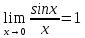 #2 Екінші тамаша шек *+ 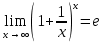 2. Анықталған интегралдық қасиеті: *+ 2. Анықталған интегралдық қасиеті: +++ 2. Анықталған интегралдық қасиеті: +++ 2. Анықталған интегралдық қасиеті: +++ 2. Анықталған интегралдық қасиеті: +++ #3 С тұрақты шаманың шегі тең: *+с шамасының өзіне #4 Егер 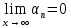 , онда , онда 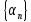 тізбегі ... деп аталады:*+шексіз аз тізбегі ... деп аталады:*+шексіз аз #5 Егер 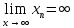 , онда , онда 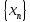 тізбегі ... деп аталады:*+шексіз үлкен тізбегі ... деп аталады:*+шексіз үлкен#6 Шектің нүктедегі қасиеті:*+ 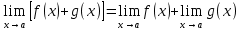 #7 а қандай мәнінде 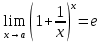 теңдігі дұрыс:*+ теңдігі дұрыс:*+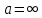 #8 Төменде келтірілген әрекеттердің қайсысы шектердің анықталмағандығын ашу тәсіліне жатады?Бөлшектің алымы мен бөлімін аргументтің ең жоғары дәрежесіне мүшелеп бөлу #9 Төменде келтірілген әрекеттердің қайсысы шектердің анықталмағандығын ашу тәсіліне жатады?Көпмүшелікті көбейткіштерге жіктеу #10 Төменде келтірілген әрекеттердің қайсысы шектердің анықталмағандығын ашу тәсіліне жатады? #11 Төменде келтірілген әрекеттердің қайсысы шектердің анықталмағандығын ашу тәсіліне жатады? #12Шектің нүктедегі қасиеті: *+ 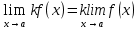 #13 Шектің нүктедегі қасиеті: *+ 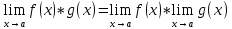 #14 Шектің нүктедегі қасиеті #1 Радийдің ыдырау жылдамдығы әрбір уақыт мезетінде, оның массасына: Пропорционал #2 t уақыт мезетінде радийдің массасы x г болсын делік. Олай болса радийдың ыдырау жылдамдығы 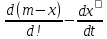 #3 Егер 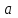 - А затының бастапқы концентрациясы, - А затының бастапқы концентрациясы, 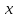 - реакция басталуынан - реакция басталуынан 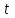 уақыт өткеннен кейінгі бір литрге шаққанда әрекеттескен мольдер саны болса, онда реакция жылдамдығы уақыт өткеннен кейінгі бір литрге шаққанда әрекеттескен мольдер саны болса, онда реакция жылдамдығы 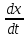 болады да, ал осы мезеттегі әрекеттесу массасы.... a-x болады да, ал осы мезеттегі әрекеттесу массасы.... a-x #4 Егер 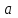 - А затының бастапқы концентрациясы, - А затының бастапқы концентрациясы, 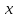 - реакция басталуынан - реакция басталуынан 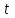 уақыт өткеннен кейінгі бір литрге шаққанда әрекеттескен мольдер саны болса, ал осы мезеттегі әрекеттесу массасы уақыт өткеннен кейінгі бір литрге шаққанда әрекеттескен мольдер саны болса, ал осы мезеттегі әрекеттесу массасы 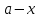 онда реакция жылдамдығы онда реакция жылдамдығы 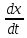 =k(a-x) =k(a-x)#5 Егер 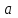 - А затының бастапқы концентрациясы, - А затының бастапқы концентрациясы,  - реакция басталуынан - реакция басталуынан  уақыт өткеннен кейінгі бір литрге шаққанда әрекеттескен мольдер саны болса, онда реакция жылдамдығы уақыт өткеннен кейінгі бір литрге шаққанда әрекеттескен мольдер саны болса, онда реакция жылдамдығы  болады да, ал осы мезеттегі әрекеттесу массасы болады да, ал осы мезеттегі әрекеттесу массасы  . Әрекеттесетін массалар қай заңға сәйкес . Әрекеттесетін массалар қай заңға сәйкес  =k(a-x) =k(a-x)#6 А және В заттарының бастапқы концентрациялары  және және  болсын; t уақытта А және В затының әрекеттескен моль санын х; А затының әрбір молі В затының молімен қосылғандықтан, екі заттан да әрекеттескен моль мөлшері бірдей болады деп алайық.t уақыт мезетінде реакция жылдамдығы болсын; t уақытта А және В затының әрекеттескен моль санын х; А затының әрбір молі В затының молімен қосылғандықтан, екі заттан да әрекеттескен моль мөлшері бірдей болады деп алайық.t уақыт мезетінде реакция жылдамдығы  болады. А затының массасы болады. А затының массасы  , ал В затының қолданыстағы массасы , ал В затының қолданыстағы массасы  тең. Масса заңына сәйкес тең. Масса заңына сәйкес =k(a-x) (b-x) =k(a-x) (b-x)#7 Әрекеттесетін массалар заңына сәйкес  мұндағы k-... , химиялық процестің шартынан, түрінен тәуелді. Пропорционалды коэф мұндағы k-... , химиялық процестің шартынан, түрінен тәуелді. Пропорционалды коэф |
