Сетевой график. Сетевой моделью называется ориентированный граф, отражающий последовательность и организационнотехнологические взаимосвязи между работами, выполнение которых необходимо для достижения поставленной цели.

• Название: Сетевой моделью называется ориентированный граф, отражающий последовательность и организационнотехнологические взаимосвязи между работами, выполнение которых необходимо для достижения поставленной цели.
• Анкор: Сетевой график
• Дата: 14.03.2022
• Размер: 2.2 Mb.
• Имя файла: Сетевой график.doc
• Тип: Документы; #396875

Сетевая модель с требуемой степенью детализации отображает взаимосвязь отдельных работ по возведению объекта (комплекса) и даёт возможность осуществить математический анализ календарного плана, прогнозировать его будущее состояние, а также оценивать эффективность принимаемых решений.

Сетевой моделью называется ориентированный граф, отражающий последовательность и организационно-технологические взаимосвязи между работами, выполнение которых необходимо для достижения поставленной цели.

Сетевая модель, представленная графически на плоскости с рассчитанными временными и ресурсными параметрами, называется сетевым графиком. Сетевые графики используются для расчёта временных параметров и оптимизации календарных планов.

Правила построения сетевых графиков

Для построения сетевого графика необходимо выявить последовательность и взаимосвязь работ: какие работы необходимо выполнить, и какие условия обеспечить, чтобы можно было начать данную работу, какие работы можно и целесообразно выполнять параллельно с данной работой, какие работы можно начать после окончания данной работы. Эти вопросы позволяют выявить технологическую взаимосвязь между отдельными работами, обеспечивают логическое построение сетевого графика и его соответствие моделируемому комплексу работ.

Уровень детализации сетевого графика зависит от сложности строящегося объекта, количества используемых ресурсов, объёмов работ и продолжительности строительства.

Имеется два типа сетевых графиков:

• вершины - работы

• вершины – события
Сетевые графики типа «вершины - работы».
Элементами такого графика являются работы и зависимости. Работа представляет собой определенный производственный процесс, требующий затрат времени и ресурсов для его выполнения, и изображается прямоугольником. Зависимость (фиктивная работа) показывает организационно-технологическую связь между работами, не требующую затрат времени и ресурсов, изображается стрелкой. Если между рабо­тами имеется организационный или технологический перерыв, то на зависимости указывается длительность этого перерыва. Пример сетевого графика «вершины - работы» приведен на рис. 6.1.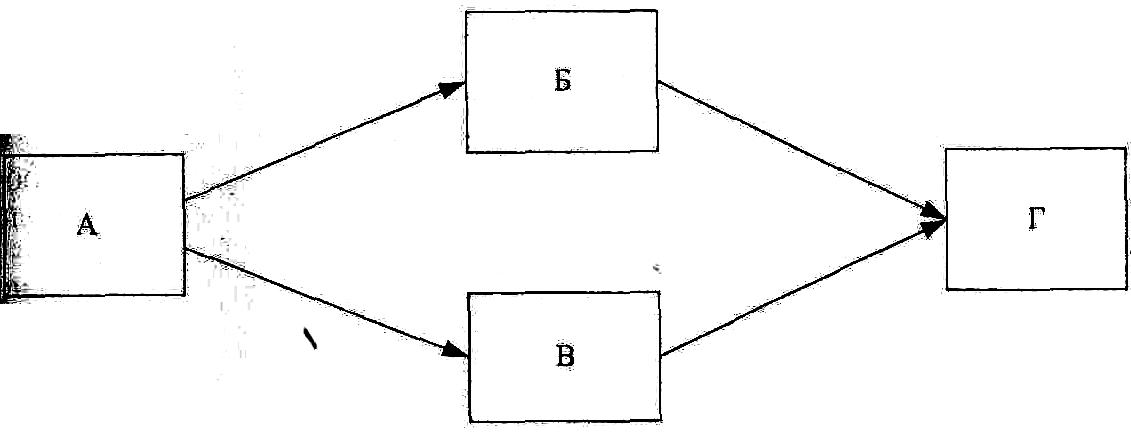



Рис. 6.1. Сетевой график типа «вершины - работы»

Если работа сетевого графика «вершины - работы» не имеет предшествующих работ, то она является исходной работой этого графика. Если работа не имеет последующих работ, то она является завершающей работой сетевого графика. В сетевом графике «вершины - работы» не должно быть замкнутых контуров (циклов), т.е. зависимости не должны возвращаться в ту работу, из которой они вышли.
Сетевые графики типа «вершины-события».
Элементами такого типа графиков являются работы, зависимости и события. Работа изображается сплошной стрелкой, зависимость – пунктирной. Событие представляет собой результат одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ, и изображается кружком.

В сетевых графиках этого типа каждая работа находится между двумя событиями: начальным, из которого она выходит, и конечным, в которое она входит. События сетевого графика нумеруются, поэтому каждая работа имеет код, состоящий из номеров её начального и конечного события. Например, на рис. 6.2 работы закодированы как (1,2); (2,3); (2,4); (4,5).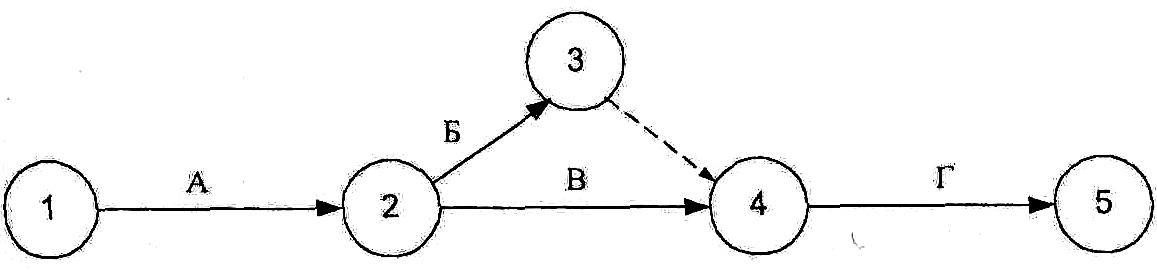



Рис.6.2. Сетевой график «вершины - события»

Если событие сетевого графика «вершины-события» не имеет предшествующих работ, то оно является исходным событием этого графика. Следующие непосредственно за ним работы называются исходными. Если событие не имеет последующих работ, то оно является завершающим событием. Входящие в него работы называются завершающими.

Для правильного отображения взаимосвязей между работами необходимо соблюдать следующие основные правила построения сетевого графика «вершины-события»:

1. При изображении одновременно или параллельно выполняемых работ (например, работ «Б» и «В» на рис.6.2) вводятся зависимость (3,4) и дополнительное событие (3).

2. Если для начала работы «Г» необходимо выполнить работы «А» и «Б», а для начала работы «В» – только работу «А», то вводится зависимость и дополнительное событие (рис.6.3.).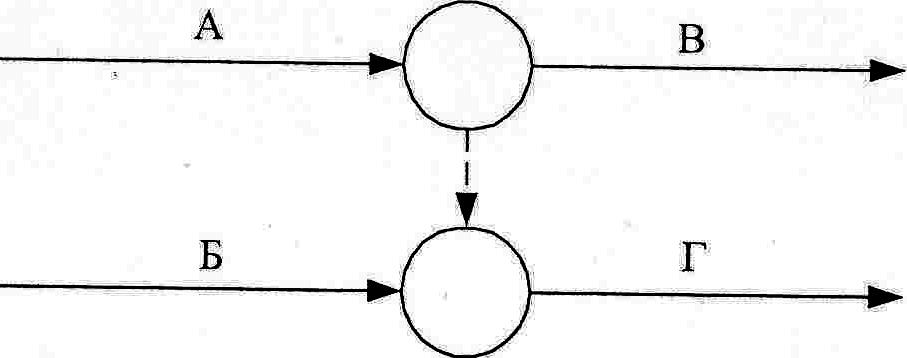



Рис.6.3. Изображение зависимости между работами

3. В сетевом графике не д.б. замкнутых контуров (циклов), т.е. цепочки работ, возвращающейся к тому событию, из которого они вышли (рис.6.4).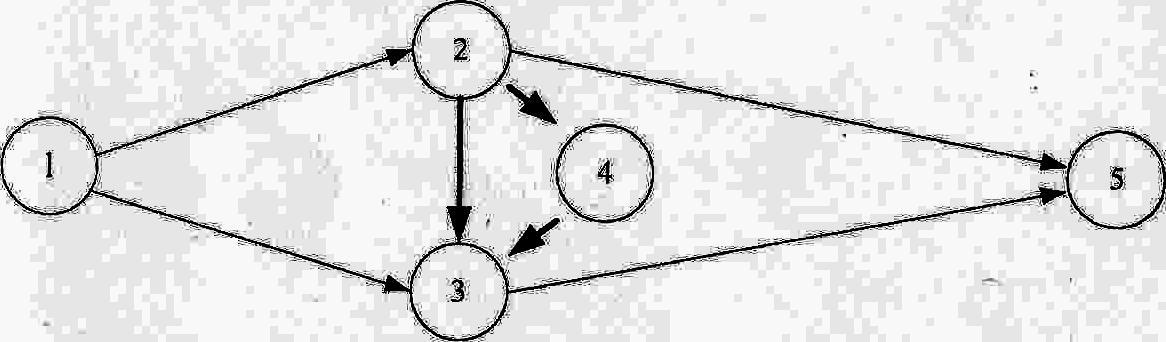



Рис. 6.4. Пример замкнутого контура (2,4,3,2)

4. В сетевом графике при поточной организации строительства вводятся дополнительные события и зависимости (рис. 6.5.).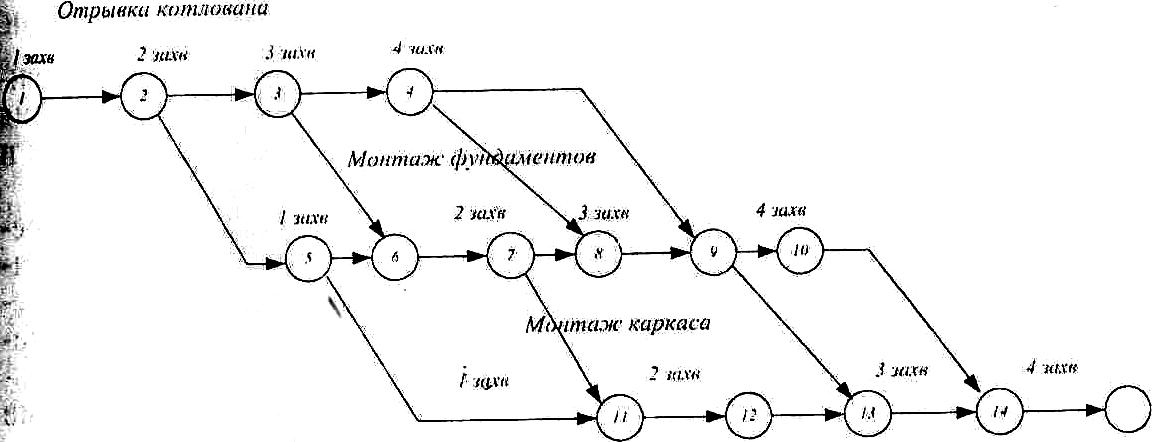



Рис. 6 5. Пример изображения потоков однородных работ
Сравнение сетевых графиков типа «вершины-работы» и «вершины-события»
Сетевые графики типа «вершины-события» имеют более давнюю историю, они появились в 50-х годах. И лишь в конце 60-х годов появились сетевые графики типа «вершины-работы» В настоящее время сетевые графики типа «вершины-работы» приобретают всё более широкое применение по следующим причинам.

1. Отсутствие событий и пунктирных зависимостей позволяет определить взаимосвязи работ до построения сетевого графика по таблице исходных данных. Каждой работе присваивается постоянный номер (код), не зависящий от изменений и дополнений в сетевом графике. Обособленное положение каждой работы позволяет ввести специальные коды для всех исполнителей.

2. Более удобное построение сетевого графика. Все прямоугольники могут быть нарисованы на листе, а затем между ними расставлены организационно-технологические зависимости. Введение новых работ и связей, так же как исключение ранее существующих, производится без изменения топологии сетевого графика. Для сетевых графиков типа «вершины-события» этого сделать нельзя, так как работы находятся между двумя событиями, а это предполагает другую логику.

3. Написание прикладных программ для сетей типа «вершины-работы» является наиболее простым делом, поэтому большинство современных прикладных программ применимо только для таких сетевых графиков

4. Сетевые графики типа «вершины-работы» адаптированы к стандартам управления и используются в специализированных пакетах программ планирования и оперативного управления.

Временные параметры сетевого графика

Каждая работа сетевого графика имеет временную оценку – продолжительность. Продолжительность (t) выполнения работы измеряется в единицах времени: часах, днях, неделях и т.д.

Любая непрерывная последовательность работ в сетевом графике называется путём. Путь от исходной до завершающей работы (события) является полным путём сетевого графика. Если известна продолжительность выполнения каждой работы, то может быть определена продолжительность пути. Продолжительность любого пути равна сумме продолжительностей составляющих его работ. Полный путь, имеющий наибольшую продолжительность, называется критическим.

Продолжительность критического пути (Т_кр) определяет общую продолжительность строительства. Следовательно, чтобы сократить продолжительность строительства, необходимо уменьшить продолжительность критических работ, т.е. работ, находящихся на критическом пути. Одной из главных задач руководителей строительства является тщательный контроль за соблюдением установленных продолжительностей выполнения именно этих работ, изыскание путей их сокращения и принятие оперативных мер по предотвращению их срыва

Для определения продолжительности критического пути и сроков выполнения каждой работы определяют следующие временные параметры сетевой модели: раннее начало работы – t^pн, раннее окончание работы – t^po; позднее начало работы – t^пн, позднее окончание работы – t^по; полный резерв времени – R; свободный резерв времени – r.

Раннее начало работы – самый ранний момент начала работы. Раннее начало исходных работ сетевого графика равно нулю. Раннее начало любой работы равно максимальному раннему окончанию предшествующих работ.

Раннее окончание работы – самый ранний момент окончания данной работы. Он равен сумме раннего начала и продолжительности работы.

Позднее окончание работы – самый поздний момент окончания работы, при котором продолжительность критического пути не изменится. Позднее окончание завершающих работ равно продолжительности критического пути. Позднее окончание любой работы равно минимальному позднему началу последующих работ.

Позднее начало работы – самый поздний момент начала работы, при котором продолжительность критического пути не изменится. Он равен разности между поздним окончанием данной работы и ее продолжительностью.

У работ критического пути ранние и поздние сроки начала и окончания равны между собой, поэтому они не имеют резервов времени. Работы, не лежащие на критическом пути, имеют резервы времени.

Полный резерв времени – максимальное время, на которое можно увеличить продолжительность работы или перенести её начало без увеличения продолжительности критического пути. Он равен разности между поздним и ранним сроком начала или окончания работы.

Свободный резерв времени – время, на которое можно увеличить продолжительность работы или перенести её начало, не изменив при этом раннего начала последующих работ. Он равен разности между ранним началом последующей работы и ранним окончанием данной работы.

Расчёт сетевого графика «вершины-работы»

Для расчёта сетевого графика «вершины-работы» прямоугольник, изображающий работу, делят на 7 частей (рис. 6.6). В верхних трёх частях прямоугольника записываются раннее начало, продолжительность и раннее окончание работы, в трёх нижних позднее начало, резервы времени и позднее окончание. Центральная часть содержит код (номер) и наименование работы.

Расчёт сетевого графика начинается с определения ранних сроков. Ранние начала и окончания вычисляются последовательно от исходной до завершающей работы. Раннее начало исходной работы равно 0, раннее окончание – сумме раннего начала и продолжительности работы:

t^ро = t^рн + t

Например, для работы (1): t^po₁ = t^pн₁ + t₁ = 0 + 2 = 2.

Трн	t	tpo
Код и наименование работы
tпн	R/r	tпo1

Рис. 6.6. Работа в сетевом графике «вершины-работы»

Раннее начало последующей работы равно раннему окончанию предыдущей работы. Если данной работе непосредственно предшествуют несколько работ, то её раннее начало будет равно максимальному из ранних окончаний предшествующих работ:

t^pн = max { t^po_предш}.

Например, для работы (5):

t^pн₅ = max { t^po₂; t^po₃} = max {7;5} = 7.

Таким образом, определяются ранние сроки всех работ сетевого графика и заносятся в верхние правую и левую части.

Раннее окончание завершающей работы определяет продолжительность критического пути.

Расчёт поздних сроков ведется в обратном порядке от завершающей до исходной работы. Позднее окончание завершающей работы равно её раннему окончанию, т.е. продолжительности критического пути: t^по₁₀ = 20

Позднее начало определяется как разность позднего окончания и продолжительности:

t^пн = t^по - t

Например, для работы (10): t^пн₁₀ = t^по₁₀ = t₁₀ - 20 - 1 = 19. Позднее начало последующих работ становится поздним окончанием предшествующих работ. Если за данной работой непосредственно следуют несколько работ, то её позднее окончание будет равно минимальному из поздних начал последующих работ:

t^по = min { t^пн_посл}.

Например, для работы (5):

t^по₅ = min { t^пн₇; t^пн₈; t^пн₉;} = min {17;15;12} = 12.

Подобным образом определяются поздние сроки всех работ сетевого графика и записываются в левую и правую нижние части.

Полный резерв времени, равный разности поздних и ранних сроков, заносится в числитель середины нижней части:

R = t^пн - t^PH = t^по - t^ро

Например, для работы (3):

R₃ = t^пн₃ - t^рн₃= 4 - 2 = 2 = t^по₃ - t^po₃ = 7 - 5 = 2

Свободный резерв времени, равный разности между минимальным ранним началом последующих работ и ранним окончанием данной работы, записывается в знаменатель середины нижней части:

r = min { t^рн_посл} - t^ро.

Например, для работы (3):

r₃ = min { t^рн₅; t^рн₆} - t^ро₃ = min {7,5} – 5 = 5 – 5 = 0.

Свободный резерв всегда меньше или равен полному резерву работы.

Пример расчёта сетевого графика «вершины - работы» приведен на рис. 6.7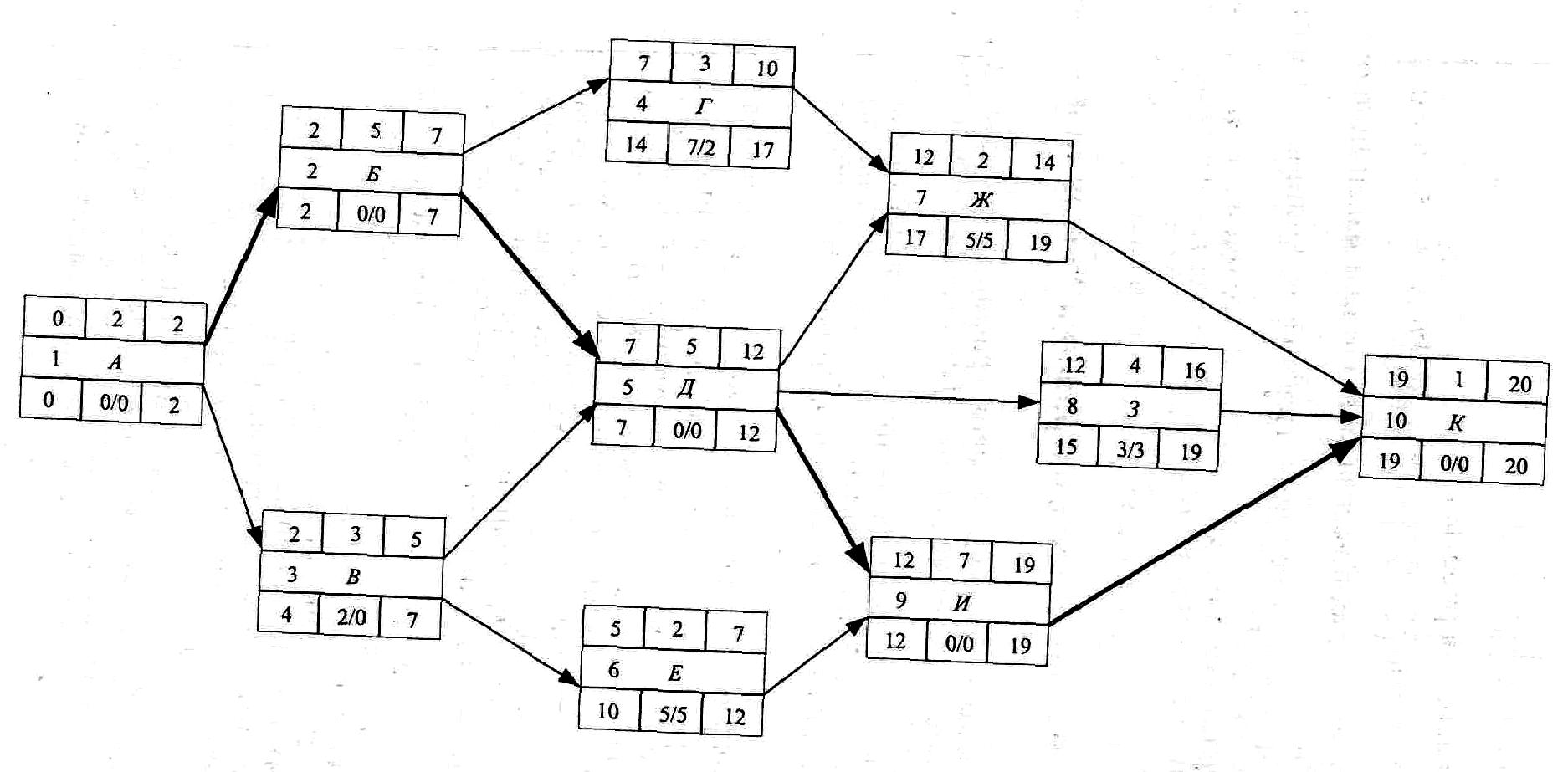



Рис. 6.7. Пример расчета сетевого графика «вершины-работы»

Последовательность работ с нулевыми резервами времени является критическим путём сетевого графика. В данном примере работы 1, 2, 5, 9, 10 находятся на критическом пути, продолжительность которого равна Т_кр = 20.

Расчёт сетевого графика "вершины-события"

На рис. 6.8 приведен сетевой график «вершины-события», включающий те же работы, что и график «вершины-работы», (рис. 6.7)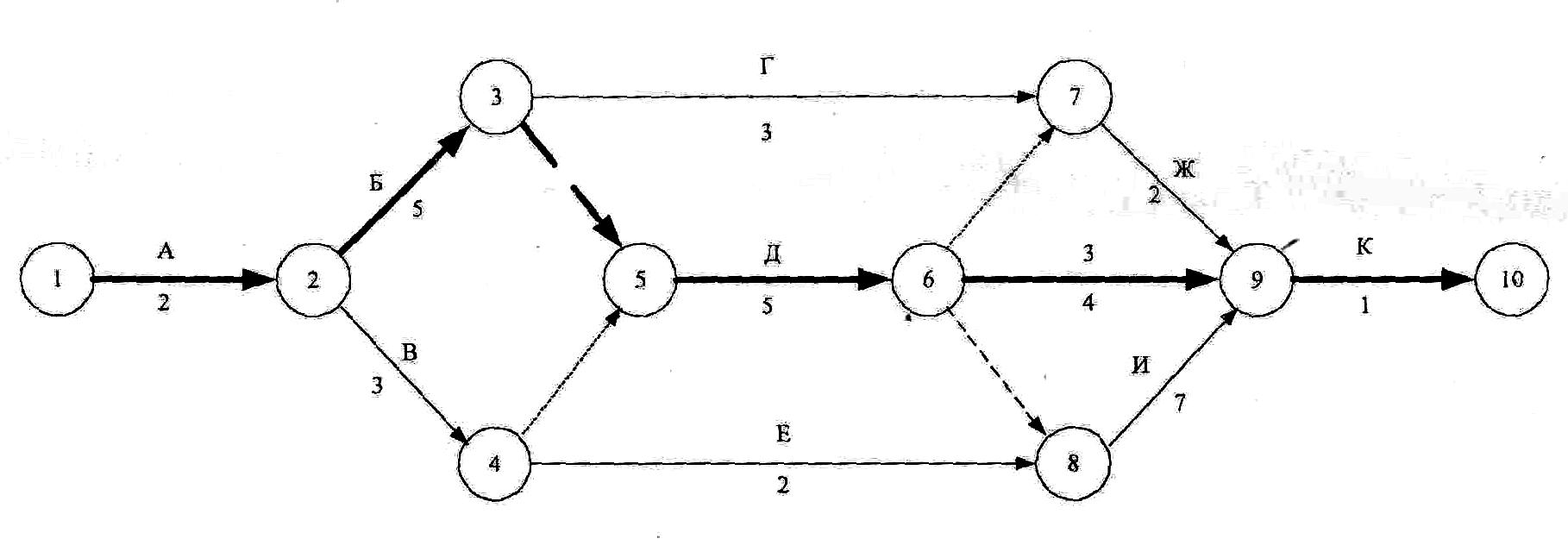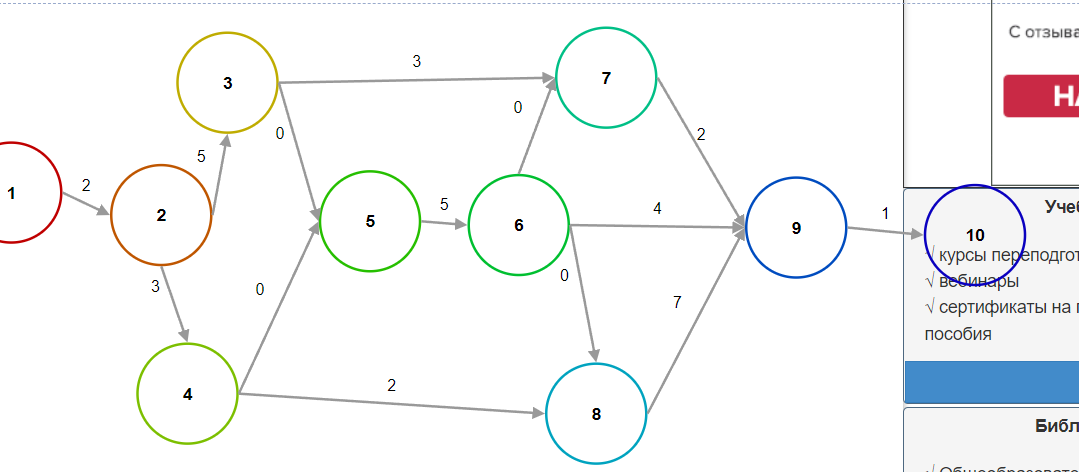





Рис. 6.8 Пример сетевого графика «вершины-события»

Для расчёта такого графика имеется несколько алгоритмов Наиболее распространенные из них это алгоритм расчёта сетевого графика в табличной форме и непосредственно на графике.

Алгоритм расчёта сетевого графика в табличной форме

Для расчёта сетевого графика в таблице необходимо, чтобы события были пронумерованы следующим образом: номер начального события каждой работы должен быть меньше номера её конечного события. Исходному событию присваивается первый номер, а все последующие события получают номера в порядке возрастания от исходного до завершающего. После нумерации каждая работа получает свой код, соответствующий номерам её начального и конечного событий.

Исходные данные из графика для расчёта заносятся в графы 1, 2 и 3 таблицы (см. табл. 6.2). Все эти три графы заполняются одновременно.

В графу 1 заносятся номера начальных событий предшествующих работ. Например, для работы (7,9) (рис. 6.8} предшествующими являются работа (3,7) и зависимость (6,7), следовательно, в гр. 1 заносятся номера начальных событий этих работ 3 и 6.

В гр. 2 заносятся коды работ и зависимостей в порядке возрастания начальных номеров событий, т.е. сначала работы, выходящие из события 1, затем из события 2 и т.д.

В гр. 3 проставляются продолжительности работ.

Таблица 6.2

Расчёт сетевого графика в таблице

Номера начальных событий предшествующих работ	Код работ (i, j)	Продолжительность работ	Раннее начало работ tрн(i,j)	Раннее окончание работ tро(i,j)	Позднее начало работ tпн(i,j)	Позднее окончание работ tпо(i,j)	Полный резерв времени работ R(i,j)	Свободный резерв времени работ R(i,j)
1	2	3	4	5	6	7	8	9
-	(1,2)	2	0	2	0	2	0	0
1	(2,3)	5	2	7	2	7	0	0
1	(2,4)	3	2	5	4	7	2	0
2	(3,5)	0	7	7	7	7	0	0
2	(3,7)	3	7	10	14	17	7	2
2	(4,5)	0	5	5	7	7	2	2
2	(4,8)	2	5	7	10	12	5	5
3,4	(5,6)	5	7	12	7	12	0	0
5	(6,7)	0	12	12	17	17	5	0
5	(6,8)	0	12	12	12	12	0	0
5	(6,9)	4	12	16	15	19	3	3
3,6	(7,9)	2	12	14	17	19	5	5
4,6	(8,9)	7	12	19	12	19	0	0
6,7,8	(9,10)	1	19	20	19	20	0	0

Ранние сроки начала и окончания работ рассчитываются по таблице сверху вниз. Раннее начало работ, выходящих из первого события, равно нулю. Раннее окончание – сумме раннего начала и продолжительности работы:

t^ро_(1,1) = t^рн_(1,1) + t_(i,1)

Например, для работы (1,2):

t^ро_(1,2) = t^рн_(1,2) + t_(1,2) = 0 + 2 = 2

Раннее начало последующих работ равно максимальному из ранних окончаний предшествующих работ:

t^pн_(i,k) = max t^po_(i,1)

Например, для работы (5,6):

t^pн_(5,6) = max { t^po_(3,5); t^po_(4,5)} = max {7;5} = 7.

Подобным образом определяются ранние начала и окончания всех работ и заносятся в графы 4 и 5 табл. 6.2.

Максимальное раннее окончание работ, входящих в завершающее событие, определяет продолжительность критического пути. В рассматриваемом примере Т_кр = 20.

Поздние сроки начала и окончания работ записываются в графы 6 и 7 табл. 6.2 Расчёт ведется в таблице снизу вверх.

Для работ, входящих в завершающее событие, позднее окончание равно продолжительности критического пути:

t^по_(9,10) = 20.

Позднее начало любой работы определяется разностью между ее поздним окончанием и продолжительностью:

t^пн_(i,j) = t_(i,j) - t_(i,j)

Например, для работы (9,10):

t^пн_(9,10) = t^по_(9,10) - t_(9,10) = 20 - 1 = 19

Позднее окончание любой работы равно наименьшему позднему началу последующих работ: t_(i,j) = min { t^пн_(j,k) }.

Например, для работы (2,4).

t^по_(2,4) =min { t^пн_(4,5) ; t^пн_(4,8) } = min{7;10}= 7

Подобным образом определяются поздние сроки всех работ сетевого графика.

Полный резерв времени равен разности поздних и ранних сроков:

R_(i,j) = t^по_(i,j) - t^ро_(i,j) = t^пн_(i,j) - t^по_(i,j)

Например, для работы (2,4):

R_(2,4) = t^по_(2,4) - t^ро_(2,4) = 7 – 5 = 2 = t^пн_(2,4) - t^рн_(2,4) = 4 – 2 = 2

Полный резерв времени заносится в графу 8 табл. 6.2.

У работ критического пути полный резерв времени равен нулю. Определяем критические работы, т.е. работы, лежащие на критическом пути, это - (1,2); (2,3); (3,5); (5,6); (6,8) (8,9), .,(9,10) Критический путь рассматриваемого сетевого графика (рис 38) будет (1,2,3,5,6,8,9,10).

Свободный резерв времени заносится в графу 9 табл. 6.2 и определяется разностью между ранним началом последующей работы и ранним окончанием данной работы:

r_(i,j) = t^рн_(j,k) - t^ро_(i,j)

Например, для работы (3,7):

r_(3,7) = t^рн_(7,9) - t^ро_(3,7) = 12 – 10 = 2.

Свободный резерв времени работы всегда меньше или равен её полному резерву:

r_(i,j)  R_(i,j)

По вышеописанному алгоритму все расчеты производятся в таблице 6.2, используя приведенные формулы.

Алгоритм расчёта непосредственно на сетевом графике

Для расчёта непосредственно на сетевом графике каждое событие делится на 4 сектора (рис. 6.9); секторный метод.

Первоначально определяются ранние начала работ сетевого графика. Расчёт ведется слева направо от исходного до завершающего события. В левый сектор исходного события (1) (рис. 6.10) записываем «0», так как раннее начало работ, выходящих из этого события равно нулю. У исходных работ сетевого графика нет предшествующих работ, поэтому в нижний сектор также записываем «0».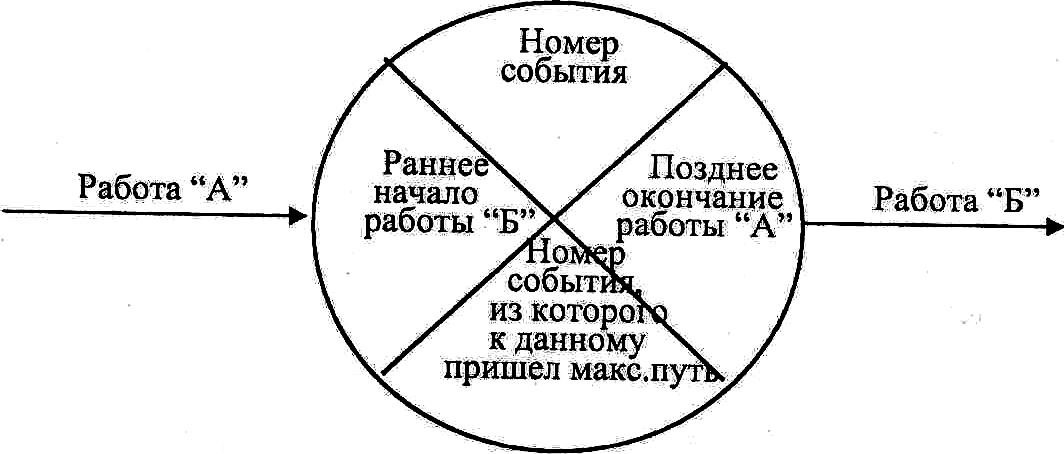



Рис. 6.9. Содержание секторов события.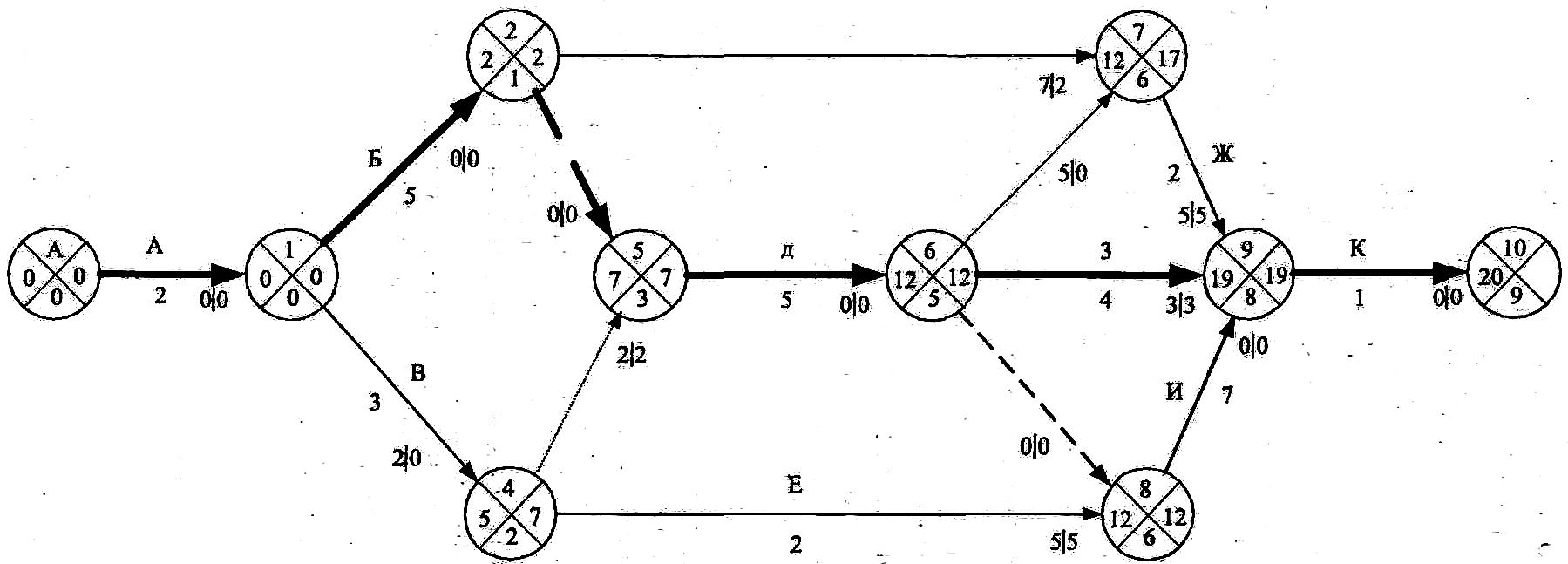



Рис. 6.10. Пример расчета на сетевом графике «вершины-события»

Раннее начало последующих работ равно максимальному раннему окончанию предшествующих работ, т.е. максимальной сумме раннего начала и продолжительности предшествующих работ:

t^рн_(j,k) = max {t^рн_(i,j) + t_(i,j)}

Например, для работы (7,9):

t^рн_(7,9) = max {(t^рн_(3,7) + t_(3,7));( t^рн_(6,7) + t_(6,7))} = max {(7 + 3);(12 + 0)} = 12

B левый сектор события (7) записываем 12 – раннее начало работы (7,9), в нижний пишем 6 – номер события, из которого к данному идёт максимальный путь. Подобным образом определяются ранние начала всех работ. Работы, выходящие из одного события, имеют одинаковые ранние начала.

В левый сектор завершающего события (10) заносится максимальная величина из сумм ранних начал и продолжильностей завершающих работ – это и будет продолжительность критического пути. Для рассматриваемого примера:

Т_кр = t^рн_(9,10) + t_(9,10) = 19 + 1 = 20.

В левый сектор события (10) заносим 20, в нижний – событие (9).

Далее определяются критические работы. Критический путьзавершает событие (10), в нижнем секторе которого записано 9. Следовательно, событие (9) также находится на критическом пути, в нижнем секторе которого записано 8, т.е. критический путь проходит через событие (8), в нижнем секторе которого стоит цифра 6, значит и событие (6) лежит на критическом пути и т.д. до исходного события. Критический путь в рассматриваемом примере проходит события (1,2,3,5,6,8,9,10), критические работы: (1,1); (2,3); (3,5); (5,6); (6,8); (8,9); (9,10). Позднее окончание работ определяется справа налево от завершающего до исходного события.

Позднее окончание завершающих работ равно продолжительности критического пути, поэтому в правый сектор события (10) проставляется 20.

Позднее окончание предшествующих работ равно минимальной разности поздних окончаний и продолжительностей последующих работ:

t_(i,j) = min{t_(j,k) - t_(j,k)}

Например, для работы (2,4):

t_(2,4) = min{(t_(4,5) - t_(4,5));(t_(4,8) - t_(4,8))} = mm{(7 - 0);(l2 - 2)} = 7

В правый сектор события (4) записываем 7. Все работы, входящие в одно событие, имеют одинаковые поздние окончания.

После расчёта ранних и поздних сроков определяются резервы времени.

Полный резерв времени работы равен разности между поздним окончанием и суммой раннего начала и продолжительности этой работы:

R_(i,j) = t^по_(i,j) - (t^рн_(i,j) - t_(i,j))

Например, для работы (3,7).

R_(3,7) = t^по_(3,7) - (t^рн_(3,7) - t_(3,7)) = 17 - (7 + 3) = 7.

Свободный резерв времени работы равен разности между ранним началом последующей работы и суммой раннего начала и продолжительности данной работы.

r_(i,j) = t^рн_(j,k) = (t^рн_(i,j) + t_(i,j))

Например, для работы (3,7):

r_(3,7) = t^рн_(7,9) = (t^рн_(3,7) + t_(3,7)) = 12 - (7 + 3) = 2.

Резервы времени работ и зависимостей записываются на графике под стрелкой полный резерв слева, свободный справа.

Корректировка сетевого графика

После расчёта временных параметров сетевого графика производится их анализ с целью установления соответствия заданным ограничениям.

Анализ начинается со сравнения продолжительности критического пути с нормативной или заданной, определяемой контрактом на строительство. Если продолжительность критического пути превышает установленные ограничения, то производится корректировка сетевого графика по времени. Корректировка по времени имеет цель сократить общую продолжительность работ, т.е. длину критического пути и других путей до величины, соответствующей заданному сроку ввода объекта. Сокращение продолжительности может производиться следующими способами:

1. сокращение продолжительности критических работ за счёт резервов времени некритических работ и перераспределения ресурсов,

2. сокращение продолжительности критических работ за счёт привлечения дополнительных ресурсов,

3. пересмотр топологии сетевого графика, т.е. изменение организационно-технологической последовательности и взаимосвязи работ.