схематехника. Схемотехника

• Название: Схемотехника
• Анкор: схематехника
• Дата: 12.02.2021
• Размер: 0.84 Mb.
• Имя файла: схематехника.docx
• Тип: Документы; #176048
• страница: 4 из 9

5.2 Тізбектелген сумматор

 

Тізбектелген операнттарға арналған сумматор тек бір ғана бір разрядты сумматордан тұрады, ол ең кішісінен бастап разрядтарды кезектесіп өңдейді. Кіші разрядтарды қосып, нәтиже мен тасымалдау кіші разрядтары үшін бір разрядты сумматор бір такттіде сақталынатын қосынды өңдеп шығарады.  Келесі тактіде кіші разрядтан ауысатын a₁ және b₁ қосылмалы жаңадан түскен разрядтар жиналады.

Тізбектелген операнттар сумматоры схемасында (5.2,а суретті қара) сумматордан басқа, A,B қосылмалы қозғалатын регисторлар және S қосынды, сондай-ақ, ауысуды есте сақтайтын D-триггер бар. A,B,S регисторлары және  D-триггері синхроимпульстармен СИ тактіленеді. 5.2,6 суретте , екі операнттың қосылу операциясына 101 + 110= 1011 немесе ондық өрнекте 5 + 6 = 11 сәйкес келетін уақыттық диаграммасы көрсетілген.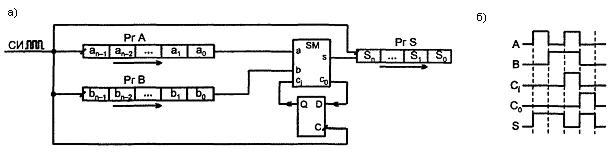

 



5.2 сурет -  Тізбектелген сумматор схемасы (а) және уақыттық диаграмма (б)

 

 

5.3 Тізбектелген тасымалдауы бар параллелді сумматор

 

Тізбектелген тасымалдануы бар параллельді операнттарға арналған сумматор тасымал тізбегімен тізбектеліп қосылған бір разрядты тізбек секілді  құрылады. Қосылу мен ауысу функциялары өздігімен екіжүзділенетін (5.5) болғандықтан, қосылу мен тасымалдың терістелуін өңдейтін бір разрядты сумматордың схемасы үшін тізбек, 5.3 суретте келтірілген түрге ие. Сумматор разрядына терістелген аргументтер берілу керек болса, олардың желісінде терістегіш бар, ал терістелген қосынды өңделсе, онда терістегіш шығыс тізбекке жалғанады.



 5.3 сурет - Тізбектелген тасымалдаулы параллельді сумматор схемасы

5.4 Параллельді тасымалдауы бар параллельді сумматор

 

Параллельді операнттар үшін параллельді тасымалдаулы сумматорлар максималды тезәсерлілікті алу үшін жасалған.

Параллельді ауысулы сумматорда разрядты торды жағалай ауысатын тізбектеп таралуы болмайды.  Барлық разрядтарда нәтиже біруақытта, уақытқа параллелді өңделеді. Берілген разряд үшін ауысу сигналы, ауысуды өңдеуге қажетті,  кірісіне барлық айнымалылар келіп түсетін, оның бар-жоғына тәуелді арнайы схемамен қалыптасады. Разрядты схемалардағы бір разрядты сумматорлар оңайлатылған, олардан ауысу шығысы талап етілмейді, қосылудың бір шығысы жеткілікті  (5.4 суретті қара).  CR белгіленуі  саrrу (ауысу) сөзінен алынған.

 



5.4 сурет - Параллельді тасымалдаулы сумматор схемасы

 

Егер берілген разряд шығысында кіріс тасымалдың бар-жоғына қарамастан тасымал  пайда болса, генерация функциясы 1 қабылдайды. Бұл  g_i = а_ib_i функциясы екені белгілі.  

Егер, берілген разряд шығысында тасымал тек кіріс тасымалы болғанда ғана пайда болса, онда айқындылық функциясы 1 қабылдайды. Бұл функция h_i = a_ivb_i. Нақтап айтқанда,  , бірақта, а_i = b_i = 1 кезінде, НЕМЕСЕ және БЕКІТУШІ НЕМЕСЕ функциялары арасында айырмашылық пайда болады, ауысым g_i = 1 үшін қалыптасады, айқындылық функциясын дизъюнкцияға ауыстыру мүмкін.  Енді, ауысым сигналы үшін өрнекті мына түрде жазуға болады  .

 i нөмірлі туынды разряд үшін былай жазуға болады

                              .                 (5.6)

ЖӘНЕ-ЕМЕС элементтеріндегі болжамды схема (стандартты элементтерде ЖӘНЕ бойынша сегіз элементке дейін болады). Алынған өрнектің аударуы ЖӘНЕ-ЕМЕС базисінде мынандай өрнекке ие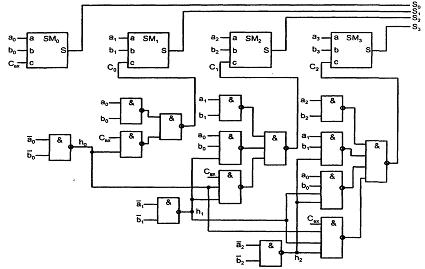

 

,

,

                                            .                                  (5.7)



 5.5 сурет - Параллельді ауысулы сумматор схемасының нұсқасы

 

Сумматор схемасы алынған өрнекке сәйкес келеді  (5.5 суретті қара). Паралельді тасымалдаулы сумматор беделін  көтеретін, разрядтылық диапазоны үлкен емес.  n = 3...4 дейін тізбектелген ауысулы,   n = 8 дейін паралельді ауысулы, n = 8 кейін топтық құрылымды сумматорлар  қолданылады.

 

6 Дәріс. АЛҚ және матрицалық көбейткіштер

 

6.1 Арифметикалы-логикалық құрылғы

 

Негізгі АЛҚ (Arithmetic-Logic Unit)  схемасы функционалды мүмкіндіктерді кеңейтетін және оның қайта құрылуын бір операциядан басқаға өтуді қамтамасыз ететін сумматор. АЛҚ негізінен төрт разрядты және разрядтылықты өсіру үшін тізбектеліп немесе паралельді тасымалданумен қалыптасу біріктіріледі. Әртүрлі технологияларда АЛҚ-ның логикалық мүмкіндіктері ұқсас болады (ТТЛШ, КМОП, ЭСЛ) .

АЛҚ ( 6.1 суретті қара) А және В операнттарының кірістеріне, S операциясын таңдау кірісіне және  орындалатын операция типін беретін сигналдың М (Mode) кірісіне ие:  логикалық (М = 1) немесе арифметикалы-логикалық  (М = 0). Операция нәтижелері F шығыстарында өңделеді, ал G және Н шығыстары АЛҚ көлемін өсіру кезінде паралельді тасымалдауды қамтамасыз ететін,  шығыстары айқындылық және генерация функцияларын береді. С_о сигналы – шығыс тасымал, ал А = В шығысы ашық коллекторлы тепе-теңдікке салыстыратын шығыс.



 

6.1 сурет - АЛҚ-ның шартты белгісі

 

АЛҚ-ның орындайтын операцияларының тізімі 6.1 кестеде келтірілген. S₃S₂S₁S₀  екілік жүйедегі қысқалық үшін оларды ондық эквивалентпен көрсеткен. Кіріс тасымал 000С_i сөзінің кіші разрядына келіп түседі. Арифметикалық операцияларда разряд аралық тасымалдар ескеріледі.

 Логикалық 16 операциялар екі айнымалының барлық функцияларын шығаруға мүмкіндік береді. Арифметикалы-логикалы операцияларда логикалық және арифметикалық операциялар бір уақытта кездеседі.

Мысалы,   - бастапқыда разряд бойынша терістеу (В), логикалық біріктіру  (АvВ) және логикалық көбейту  (АВ) операцияларын орындайды, содан кейінкөрсетілген үлгімен алынған екі төрт разрядты сандар арифметикалық түрде қосылады. 

Үлкен көлемді сөздердегі операциялар кезінде АЛҚ тізбектеліп ұйымдасып, (6.2,а суретке қара) немесе паралельді тасымалдаумен бір-бірімен қосылады  (6.3,б суретке қара).  Соңғы жағдайда, АЛҚ-мен бірге микросхема – АЛҚ жеке  айқындық және генерация функцияларын алатын жылдамдататын

тасымал блоктарын, сондай-ақ нақты формула бойынша тасымал сигналдарын шығарушы және кіріс тасымалдары қолданылады.

 

6.1 кесте – АЛҚ операцияларының тізімі

 

S	Логикалық функциялар (М=1)	Арифметикалы-логикалық функциялар (М=0)
0 1 2 3	0000	A + Ci 1111 +Ci
4 5 6 7
8 9 10 11	В АВ	A + AB + Ci A + B + Ci AB + 1111 + Ci
12 13 14 15	1111 А	A + A + Ci A v B + A + Ci A + 1111 + Ci

 

CRU блогы АЛҚ қызмет ететін барлық топтар үшін қажет болған жағдайда келесі дәреже бойынша паралель тасымалды ұйымдастыруға мүмкіндік беретін айқындылық және генерация функцияларын өңдейді (төрт АЛҚ ішінен бірнеше топтар арасында).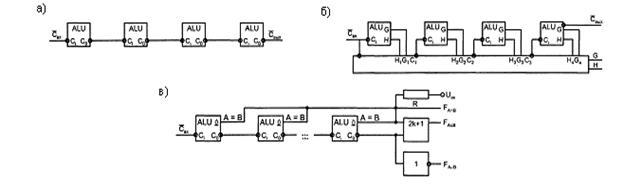



6.2 сурет -  Тізбектеліп (а) және параллельді (б)  тасымалдану кезіндегі  АЛҚ-ның өсу және топтар үшін (в) компаратор функцияларын жүзеге асыру схемалары 

 

6.2,в суретте АЛҚ топтары үшін сөздерді салыстыру үшін сигналдарды өңдеу тәсілдері көрсетілген. Тепе-теңдікке салыстыру шығысы ОК типті ығыстар үшін монтажды логика схемалары бойынша орындалады. Азайту  режимінде АЛҚ жұмысы кезінде топтардың шығысында тасымалдау сигналдарын сөздерді теңестіру сигналдарымен құрамдастырып F_a≥b  және F_a≤b функцияларын оңай алуға болады. Егер  А<В болса, онда азайту кезінде үлкен разрядтан қарыз алу туындайды  F_a≤b = 1. Егер де қарыз болмаса (А>В), онда F_a≥b = 1.

 

6.2 Матрицалы көбейткіштер

 

Матрицалы көбейткіштердің құрылымы көбейту операцияларын сипаттайтын математикалық өрнектердің құрылымымен тығыз байланысты. Екі таңбасыз екілік жүйе сандары болсын A_m = a_m-1...a_o және B_n=b_n-1...b_o. оларды еселеу "бағаналарды көбейту" схемасы бойынша орындалады. Егер сандар төрт разрядты болса m = n = 4, онда

 



 

 

a_ib_j мүшелері, мұндағы  i = 0... (m - 1) және  j = 0... (n - 1), конъюктор уақытымен паралельді түрде өңделеді. Оларды бағана бойынша әртүрлі жолмен

орындауға болатын  көбейту көбейткіштер үшін негізгі операцияларды құрайды. 

Матрицалы қайта көбейткіштер қарапайым көбейткіш блоктары (КБ) немесе көбейтіп-қосқыш блоктары (КҚБ) болуы мүмкін, соңғысы көбейткіштердің көлемінің өсуіне жағдай жасайды.

КҚБ МСБ Р = А_m х В_n + С_m + D_n операциясын жүзеге асырады, ол туындыға екі буын қосады: біреуі  көбейетін разрядтылыққа сәйкес келетін разряды, ал екіншісі m т. е. Көбейткішке екі қосылғыш қосады: біреуі  m разрядты, көбейтінді разрядымен сәйкес келетін, екіншісі n разрядты, көбейткіш разрядымен сәйкес келетін.

 

6.2.1 Көбейткішті-қосындылы блоктар.

Көбейткішті-қосындылы блоктар конъюнкторлар жинағынсыз төртразрядты операндтар үшін, өңделген а_ib_j түріндегі мүшелері  6.3, а суретте көрсетілген ( мұндағы бірразрядты  сумматор үшін қолданылған белгілеу 6.3, б суретті қара).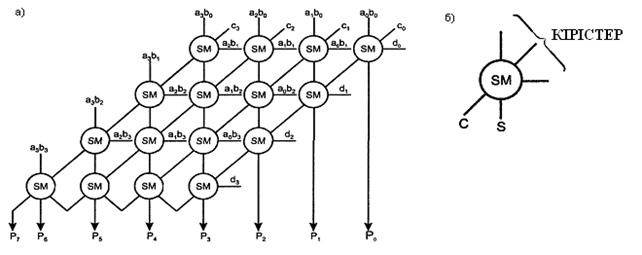

 



6.3 сурет  – Төртразрядты көбейткіштерге арналған КҚБ сызбасы (а) және  осы сызба үшін бірразрядты сумматордың белгіленуі (б)

 

Теңразрядты сандардың  КҚБ құру үшін  n² конъюкторлар және  n²  бірразрядты сумматорлар керек.

 

6.2.2 Жедел көбейту сызбалары.

Модифицирленген алгоритм бойынша көбейту процесін қарастыралық. Бұнда көбейту бірден екі разрядқа артады. Жеке көбейткіштердің қосындысын азайту функциясы көбейту уақытын едәуір қысқартады. Осыған төмендегі талдауларға негізделген  алгоритм алып келеді.

Мына көбейтіндіні есептеу керек болсын

                                 .                                (6.1)

Тікелей (6.1) қатынасын  қайта көбейту мына түрдегі жеке көбейтулерді орындаумен тікелей байланысты

                                         Ab_i2ⁱ    (i = 0...n - 1).                                           (6.2)

Мұндай көбейтулер саны  n көбейткішінің санына тең.

Мына қатынас көмегімен  (6.1) өрнегінің түрін өзгертуге болады

                                                       .                                             (6.3)

Бұл қатынас жеке көбейткіштер қосындысындағы дәрежелердің тізбектілігін сиретуге мүмкіндік тудырады. Мысалы, 6.4 суретте көрсетілгендей жұп дәрежелерді шығарып тастауға болады.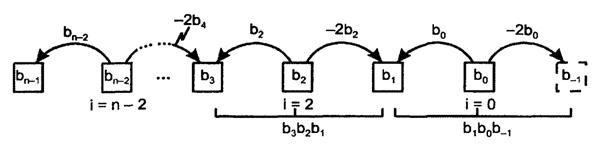  



6.4 сурет – Жұп дәрежелерді шығарып тастау

 

Жұп (тақ)  дәрежелерді шығарып тастау қалған жеке көбейтінділердің мәнін ғана өзгертіп қоймай , сонымен қатар олардың санын жуық шамамен екі есеге азайтып, көбейту нәтижесін тездетеді.  (6.3) формуласы бойынша разрядтық торды кеңейту үшін (6.1)  өрнегіндегі В көбейткіші  үшін  b₂2²,b_o2^o,b_-22^-2  жұп дәрежелі мүшелерді «көршілерге таратады».

Осыдан соң  кез-келген i-ші  разряд үшін мына түрге келтіріледі

                                                      .                                     (6.4)

Егер  (6.1) және (6.4) өрнектерін салыстырсақ, онда жеке көбейтінділер екі есе азайды. Осы алгоритмді қолданған кезде бірден  екі разрядқа көбейту туралы (i жұп разрядтан бастап коэффициенттері солдан i+1 және оңнан i-1 ).

 (6.4)  барлық  мүмкін b_i+1, b_i, b_i-1  үшін қолданып, жеке көбейтінділер үшін 6.2 кестесін құруға болады.

 

 

 6.2  кесте

bi+1	bi	bi-1	Жақша мәні	Ri/2i	Алу операциясы Ri/2i
0	0	0	0	0	А нөлмен ауыстыру
0	0	1	1	А	А көшіру
0	1	0	1	А	А көшіру
0	1	1	2	2А	А солға жылжыту
1	0	0	-2	-2А	А солға жылжыту және А қос. кодқа ауыстыру
1	0	1	-1	-А	А қос. кодқа ауыстыру
1	1	0	-1	-А	А қос. кодқа ауыстыру
1	1	1	0	0	А нөлмен ауыстыру

 

Мысал.

1010-ды  0111-ге көбейту керек болсын, яғни  10∙7 = 70. Жеке көбейтінділерді сиреткен кезде тек тақтарын ғана қалдырамыз (6.4 суретті қара).

Енді (6.4) формуласы бойынша мынаны аламыз         .

Алынған өрнектен көрініп тұрғандай  В көбейткішінің разрядтық торын солдан 1 разрядқа және оңнан 2 разрядқа кеңейту керек, яғни

В = b₄b₃b₂b₁b_ob_-1b_-2 = 0011100.

Бірінші жеке көбейтіндіге   b_ob_-1b_-2 = 100 үштігі  сәйкес келеді.  6.2 кестеден осы үштікке мына жеке көбейтінді сәйкес екенін аламыз

R_-1 = -2А∙2^-1 = -А,

оны алу үшін   қосымша А кодқа көшіру керек.  А  шамасының өзі  разрядтық көбейту тор шегінде 0001010 сияқты болып жазылуы керек, оның кері коды 1110101 және қосымша коды 1110110 болады.

Екінші жеке көбейтіндіге  b₂b₁b_o = 111 үштігі сәйкес келеді, осыдан екінші жеке көбейтінді  R₁ = 0 тең болады ( 6.2 кестені қара).

Үшінші жеке көбейтіндіге  b₄b₃b₂ = 001 үштігі сәйкес келеді, осыдан  оның түрі  R₃ = А∙2³ = 1010000  ( А-ны 3 разрядқа солға жылжыту ) келтіріледі.

Берілген көбейту нәтижесін алу үшін жеке көбейтінділерді қосу қажет болады:

       1110110

       1010000

       -----------

       1000110 = 2⁶ + 2² + 2¹ = 64 + 4 + 2 =70.

 

6.5 суретте тез көбейту алгоритмін іске асыру сызбасы көрсетілген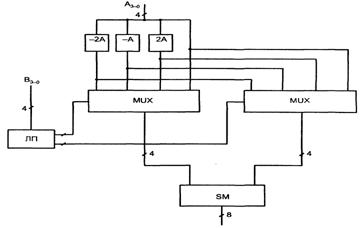



 

 6.5 сурет  – Тез көбейту сызбасы

 

 А көбейгіші (-2А, -А, 2А), сызбалық тарату қажет етпейтін  А-ның өзінен және нөлден басқа жеке көбейтінділердің барлық мүмкін варианттарын дайындайтын бірнеше түзеткіштер қатарына келіп түседі.  В көбейгіші ЛТ логикалық түрлендіргіш ретінде  түсіп, разрядтар үштіктерін сараптайды, оларды кодтайды және оларды  мультиплексорларға  (MUX) жеке көбейтінділердің сол немесе басқа варианттарының сигналдары түрінде береді

 ( 6.2 кестесін қара). Қорытынды нәтиже олардың разрядтық тордағы өзара ығысуын ескере отырып,  жеке көбейтінділерді қосу арқылы алынады. Көбейткіш өлшемділігі «4х4».