Задания для олимпиады. задания на Школьный этап всероссийской олимпиады по математике 6. Школьный этап всероссийской олимпиады по математике 202122 уч г. 6 класс Максимальная оценка каждой задачи 7 баллов
 Скачать 233.5 Kb. Скачать 233.5 Kb.
|
 Школьный этап всероссийской олимпиады по математике 2021-22 уч.г. Школьный этап всероссийской олимпиады по математике 2021-22 уч.г.6 класс Максимальная оценка каждой задачи – 7 баллов 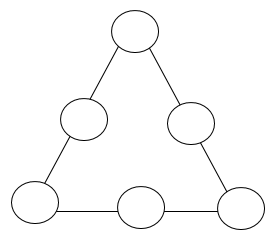 В шести кружках, расположенных в форме равностороннего треугольника, расставьте числа 31, 32, 33, 34, 35, 36 так, чтобы сумма чисел на всех трех сторонах треугольника была одинаковой и равнялась 100. Вычислите: 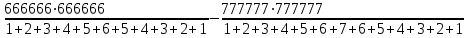 Куб с ребром 20 см разрезан на кубики с ребром 2 см. Затем все эти кубики уложили в один сплошной ряд. Чему равна длина этого ряда? В магазин доставили 6 бочонков с квасом, в них было 15, 16, 18, 19, 20 и 31 литр. В первый же день нашлось два покупателя: один купил два бочонка, другой – три, причем первый купил вдвое меньше кваса, чем второй. Не пришлось даже раскупоривать бочонки. Из шести бочонков на складе остался всего лишь один. Какой? Одуванчик утром распускается, два дня цветет желтым, на третий день утром становится белым, а к вечеру облетает. Вчера днем на поляне было 20 желтых и 14 белых одуванчиков, а сегодня 15 желтых и 11 белых. Сколько белых одуванчиков будет на поляне завтра? Критерии оценивания и решения задач: В соответствии с регламентом проведения математических олимпиад каждая задача оценивается в 7 баллов. Соответствие правильности решения и выставляемых баллов приведено в таблице. Максимальный балл в каждой задаче – 7.
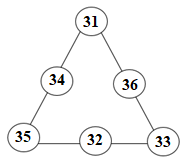 Ответ: 0  Решение: 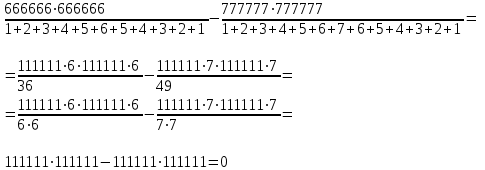 Ответ: 20 м Решение: Объем большого куба – 8000 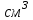 , значит в ряд уложены 1000 кубиков с ребром 2 см, то есть длина ряда равна 2000 см или 20 м. , значит в ряд уложены 1000 кубиков с ребром 2 см, то есть длина ряда равна 2000 см или 20 м.Ответ: 20-литровый бочонок Решение: Первый покупатель купил 15-литровый и 18-литровый бочонки. Второй – 16-литровый, 19-литровый и 31-литровый. Остался непроданным 20-литровый бочонок. Ответ: 9 одуванчиков Решение: Из вчерашних желтых одуванчиков 11 побелели сегодня, а остальные 20−11=9 побелеют завтра. Олимпиадные задания по математике 8 класс Приведите какое-нибудь одно решение числового ребуса ДО + РЕ + МИ + ФА = 128 (различными буквами зашифрованы различные ненулевые цифры). Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды. Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика. От чего больше толстеют: от варенья или от сгущенки? В каждой клетке клетчатой доски размером 50  50 записано по числу. Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали. Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках. 50 записано по числу. Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали. Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках. Две семьи выехали каждая на машине «Жигули» на прогулку одновременно из одного места. Обе семьи проехали на машинах одинаковые расстояния и вернулись домой в одно и то же время. В пути они отдыхали. Первая семья была в пути вдвое больше времени, чем вторая. Вторая была в пути втрое больше времени. Чем отдыхала первая. Какая из этих семей двигалась на машине быстрее? В комнате лежал небольшой мешок с яблоками. Среди 10 человек часть – рыцари (они всегда говорят правду), а остальные – лжецы (они всегда лгут). Первый из этих 10 человек зашёл в комнату, заглянул в мешок и сказал: «В мешке больше 1 яблока»; после этого он взял одно яблоко из мешка и вышел из комнаты. Потом зашел второй, и, заглянув в мешок, сказал, что в нем больше двух яблок. Затем он взял яблоко из мешка и вышел из комнаты. Так же и остальные по очереди заходили, говорили, что в мешке осталось больше 3, 4, . . . , 10 яблок, брали по яблоку и выходили из комнаты. Какое наибольшее число лжецов может быть среди этих 10 человек? Ответы на олимпиадные задания по математике 8 класс Приведите какое-нибудь одно решение числового ребуса ДО + РЕ + МИ + ФА = 128 (различными буквами зашифрованы различные ненулевые цифры). Ответ. 15 + 26 + 38 + 49 = 128. Замечание. Ответ является единственным с точностью до перестановок у слагаемых цифр в разрядах единиц или цифр в разрядах десятков. Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды. Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика. От чего больше толстеют: от варенья или от сгущенки? Ответ. От сгущенки. Решение. По условию 3м + 4с + 2в > 2м + 3с + 4в, откуда м + с > 2в. (*) По условию же 3м + 4с + 2в > 4м + 2с + 3в, откуда 2с > м + в. Складывая последнее неравенство с неравенством (*), получаем м + 3с > м + 3в, откуда с > в. В каждой клетке клетчатой доски размером 50  50 записано по числу. Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали. Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках. 50 записано по числу. Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали. Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках. Решение: Покажем, что подойдет раскраска клеток доски в шахматном порядке. Заметим, что сумма данного числа и его соседей по диагоналям равна сумме соседей этого числа по сторонам: обе суммы втрое больше данного числа. Поэтому в квадрате 2  2, находящемся в углу доски, суммы чисел в красных и синих клетках совпадают: обе они втрое больше числа, стоящего в угловой клетке доски. Также совпадают суммы чисел в красных и синих клетках любого прямоугольника 3 2, находящемся в углу доски, суммы чисел в красных и синих клетках совпадают: обе они втрое больше числа, стоящего в угловой клетке доски. Также совпадают суммы чисел в красных и синих клетках любого прямоугольника 3  2, примыкающего длинной стороной к краю доски: обе они втрое больше числа, стоящего в средней клетке стороны, примыкающей к краю доски. Наконец, совпадают суммы чисел в красных и синих клетках любого квадрата 3 2, примыкающего длинной стороной к краю доски: обе они втрое больше числа, стоящего в средней клетке стороны, примыкающей к краю доски. Наконец, совпадают суммы чисел в красных и синих клетках любого квадрата 3  3: обе они втрое больше числа, стоящего в центре квадрата. 3: обе они втрое больше числа, стоящего в центре квадрата.Разобьем доску 50  50 на квадрат 48 ? 48, квадрат 2 50 на квадрат 48 ? 48, квадрат 2  2 и два прямоугольника 2 2 и два прямоугольника 2 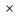 48, как показано на рисунке 3. Квадрат 48 48, как показано на рисунке 3. Квадрат 48 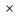 48 разобьем на квадраты 3 48 разобьем на квадраты 3 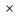 3, а прямоугольники 2 3, а прямоугольники 2 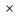 48 — на прямоугольники 3 48 — на прямоугольники 3 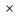 2, примыкающие длинной стороной к краю доски. В каждом из этих квадратов и прямоугольников суммы чисел, стоящих в красных и синих клетках, равны. Значит, они равны и на всей доске. 2, примыкающие длинной стороной к краю доски. В каждом из этих квадратов и прямоугольников суммы чисел, стоящих в красных и синих клетках, равны. Значит, они равны и на всей доске. Две семьи выехали каждая на машине «Жигули» на прогулку одновременно из одного места. Обе семьи проехали на машинах одинаковые расстояния и вернулись домой в одно и то же время. В пути они отдыхали. Первая семья была в пути вдвое больше времени, чем вторая. Вторая была в пути втрое больше времени. Чем отдыхала первая. Какая из этих семей двигалась на машине быстрее? Ответ. Вторая семья. Решение: 1-я семья: 2х часов - время на езду, у часов - время на отдых. 2-я семья: 3у часов - время на езду, х часов - время на отдых 2х + у = 3у + х; х = 2у. Вторая семья отдыхала в два раза больше, чем первая следовательно, она ехала быстрее первой. В комнате лежал небольшой мешок с яблоками. Среди 10 человек часть – рыцари (они всегда говорят правду), а остальные – лжецы (они всегда лгут). Первый из этих 10 человек зашёл в комнату, заглянул в мешок и сказал: «В мешке больше 1 яблока»; после этого он взял одно яблоко из мешка и вышел из комнаты. Потом зашел второй, и, заглянув в мешок, сказал, что в нем больше двух яблок. Затем он взял яблоко из мешка и вышел из комнаты. Так же и остальные по очереди заходили, говорили, что в мешке осталось больше 3, 4, . . . , 10 яблок, брали по яблоку и выходили из комнаты. Какое наибольшее число лжецов может быть среди этих 10 человек? Ответ. Рыцарей и лжецов не меньше 5. Решение: Так как 10 человек взяли по яблоку из мешка, то в мешке изначально было не меньше 10 яблок. После того, как первые четыре человека взяли по яблоку из мешка, в мешке осталось не менее 6 яблок. Значит, пятый вошедший (сказавший, что в мешке больше 5 яблок) сказал правду. Аналогично, сказали правду первые четверо. Это означает, что рыцарей не меньше 5, а лжецов не больше 10 – 5 = 5. С другой стороны, 5 лжецов среди этих 10 человек быть могло, если, например, в мешке изначально лежало 10 (или 11) яблок. Тогда первые пять человек скажут правду, а все, начиная с шестого (перед его приходом в мешке будет только 5 или 6 яблок), солгут. Шкала оценивания заданий.
|
