тезисы. Шляпина Любовь Васильевна
 Скачать 37.01 Kb.
|
|
Задачи на клетчатой бумаге Формула Пика. Беляева Кристина, 8 класс МАОУ «СОШ №74» г. Пермь Руководитель: Шляпина Любовь Васильевна Увлечение математикой начинается с размышления над какой-либо интересной темой или понравившейся задачей. Богатым источником служат различные математические конкурсы и олимпиады. Мне хочется выделить особую группу заданий, подход к решению которых интересен и оригинален. Это задачи на клетчатой бумаге. У меня возникали вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге. Изучив литературу, выяснила, что для многих задач на бумаге в клетку нет общего правила решения, конкретных способов и приёмов. Мне удалось найти формулу Пика, которая позволяет упростить решение и сэкономить время при решении задач на нахождение площадей многоугольников. Объект исследования: задачи на клетчатой бумаге. Предмет исследования: площади фигур, изображённых на клетчатой бумаге. Методы исследования: моделирование, сравнение, обобщение, изучение литературных и Интернет-ресурсов, анализ и классификация информации. Цель исследования : изучить различные способы решения задач на клетчатой бумаге и познакомиться с формулой Пика. Задачи: 1. Изучить источники и отобрать понятную информацию. 2. Решить задачи на нахождение площадей фигур, изображённых на клетчатой бумаге, геометрическими методами. 3. Решить задачи на нахождение площадей фигур, изображённых на клетчатой бумаге, с применением формулы Пика. 4. Подобрать задачи на нахождение площадей фигур на клетчатой бумаге для подготовки к ОГЭ и ЕГЭ. 5.Сравнить и проанализировать результаты исследования. 6. Подготовить презентацию для представления собранного материала. Площади фигур имеют огромное значение в геометрии, как в науке. Ведь площадь это одна из важнейших величин в геометрии. Существует множество способов нахождения площадей многоугольников. Познакомимся с некоторыми из них. Сюжет будет разворачиваться на обычном листке клетчатой бумаги. Л 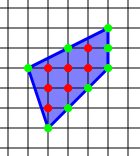 инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдем его площадь. Найти её можно по-разному. 1 способ. Можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить. S=(4*2)/2+(3*1)/2+(3*3)/2=10см² 2 способ. Вычислим площадь заштрихованной фигуры, которая «дополняет» многоугольник до прямоугольника и вычтем её из площади прямоугольника. S=4*5-1,5-4,5-4=10 см² . Заштрихованная фигура легко разбивается на прямоугольники и прямоугольные треугольники, и её площадь вычисляется без усилий. Итак, хотя многоугольник и выглядел достаточно просто, для вычисления его площади пришлось потрудиться. А если бы многоугольник выглядел более причудливо? Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри (обозначим В), а количество узлов на границе (Г) многоугольника. Получим формулу: S= В+ 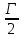 -1 . Эта замечательная и простая формула называется формулой Пика, которая была открыта в 1899 года. Формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки. 3 способ: Найдем площадь фигуры по формуле Пика. В=7, Г=8, S= В+ 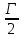-1 =7+4-1=10 см² Вычислив тремя способами, получили один и тот же результат. Сравнивая и анализируя результаты исследования можно сделать вывод: формула Пика даёт быстрое и простое решение задач на нахождение площадей фигур, вершины которых лежат в узлах решётки, т.е. нахождение площади многоугольников. В процессе исследования изучено много справочной, научно-популярной литературы, просмотрены сайты ФИПИ, РЕШУ ЕГЭ. Рассмотрены различные задачи на построение и вычисления, заданные на клетчатой бумаге, а также задачи с практическим содержанием. подобраны задачи для подготовки к итоговой и промежуточной аттестации. Эти задачи отличаются от обычных задач, изложенных в учебниках и задачниках по математике. Вычисления по формуле Пика имеет перед другими способами ряд преимуществ. Формула проста для запоминания, удобна в применении. Маленькая формула Пика заменит учащимся целый комплект формул, необходимых для решения таких задач. Работа носит исследовательский характер. Достигнута поставленная цель, решены задачи. Гипотеза: Площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии, подтвердилась. Практическая значимость: 1.Результаты данного исследования могут быть использованы в последующих работах при решении задач, связанных с бумагой в клеточку; 2.Материалы работы будут полезны при подготовке к ОГЭ и ЕГЭ; 3. Работа по данной теме позволила преодолеть психологический барьер и поверить в свои силы, что является важнейшим фактором успешного решения олимпиадных и экзаменационных задач, выступления перед аудиторией с материалом по данной теме. |