РГЗ по ОТС. ОТС РГЗ №1. Сигналы и их характеристики
 Скачать 280.38 Kb. Скачать 280.38 Kb.
|
Задание 1Сигналы и их характеристикиСигнал определяется восьмизначным равномерным кодом согласно варианту и подварианту (табл. 1), где символ «0» соответствует нулевой посылке, а символ «1» – прямоугольному видеоимпульсу напряжения с амплитудным значением 10 В и длительностью 0.1 мкс. Дан сигнал: 01111010. Требуется: Записать математическую модель сигнала в виде линейной комбинации функций Хэвисайда, построить временной график 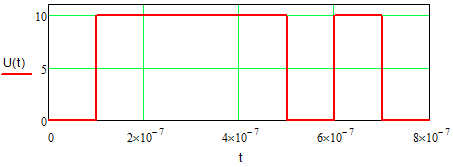 Рис 1. Временной график заданного сигнала. Найти спектр сигнала относительно базиса Уолша, построить спектральную диаграмму Функции Уолша формируются из функций Радемахера с помощью следующего соотношения:  где n – номер функции Уолша, nk – значение (0 или 1) k – разряда номера функции Уолша n, записанного в виде m – разрядного двоичного кода Грея, radk (θ) – функция Радемахера, которая имеет вид: - 3 битный код Грэя; П   одставляя все имеющиеся значения, получаем: одставляя все имеющиеся значения, получаем:  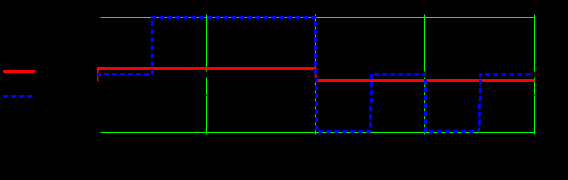  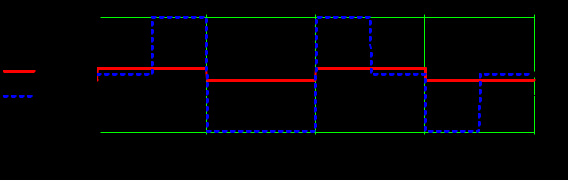 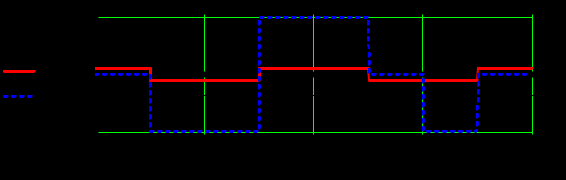 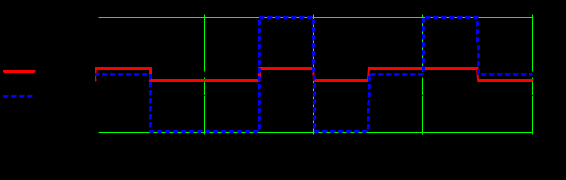 Рис 2.1. Система i -х функций Уолша  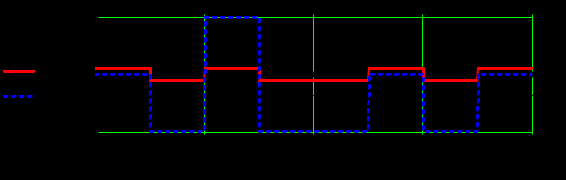 Рис 2.2.Система i -х функций Уолша (продолжение) Тогда спектром сигнала относительно базиса Уолша будет:  ; ; Рис 3. Спектральная диаграмма сигнала относительно базиса Уолша Найти аналитически спектральную плотность прямоугольного видеоимпульса длительностью 1 с и амплитудой 1 В относительно ядра Фурье Математическая модель прямоугольного видеоимпульса: Е  го спектральная плотность рассчитывается по формуле: го спектральная плотность рассчитывается по формуле: Рис 4. Спектральная плотность одиночного видеоимпульса Пользуясь свойствами преобразования Фурье, найти спектральную плотность заданного сигнала относительно ядра Фурье, построить графики её модуля и аргумента  Рис 5. Временной график заданного сигнала. Спектральная плотность прямоугольного видеоимпульса рассчитывается по формуле:  − где 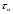 длительность импульса. длительность импульса.Используем, теорему о спектре сигнала смещённого во времени 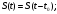 : :  − где  задержка импульса. задержка импульса.Найдём длительность и задержку для исходного сигнала: 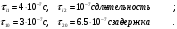  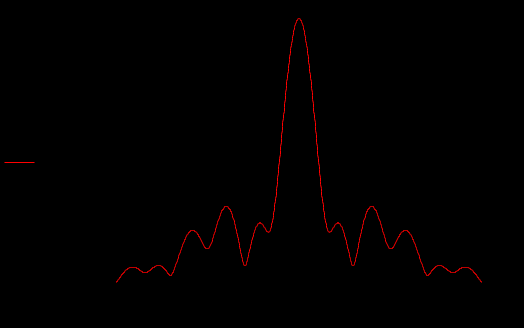 Рис 6. Модуль спектральной плотности заданного сигнала 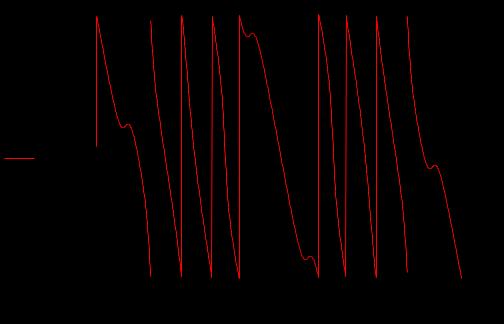 Рис 7. Аргумент спектральной плотности заданного сигнала Найти спектр периодической последовательности, полученной повторением заданного сигнала, относительно комплексного базиса Фурье, построить амплитудную и фазовую спектральные диаграммы Найденная в прошлом пункте спектральная плотность имеет форму огибающей спектральных коэффициентов ряда Фурье периодической последовательности, образованной повторением заданного импульсного сигнала. Тогда формула для нахождения спектра относительно базиса Фурье будет иметь следующий вид: 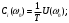 − 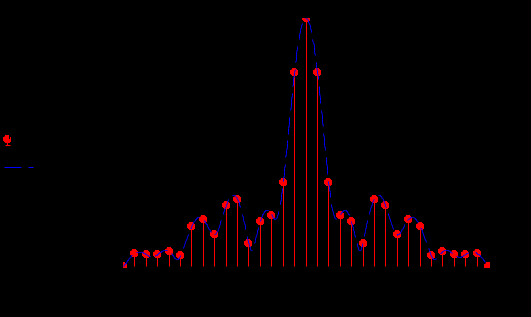 где где 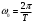 − частота заданного сигнала с периодом Т=0.8 мкс. − частота заданного сигнала с периодом Т=0.8 мкс. Рис 8. Амплитудная спектральная диаграмма 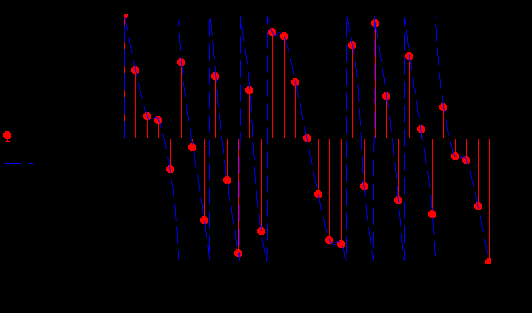 Рис 9. Фазовая спектральная диаграмма Найти автокорреляционную функцию сигнала, построить график Автокорреляционная функция сигнала есть скалярное произведение, сигнала и его смещенной копии на величину  : : Представим это произведение графически ( Δ  =107 с – смещение). =107 с – смещение). 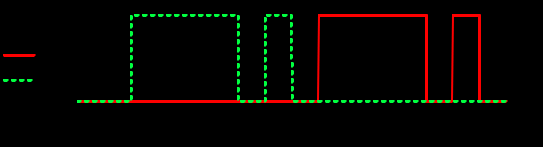 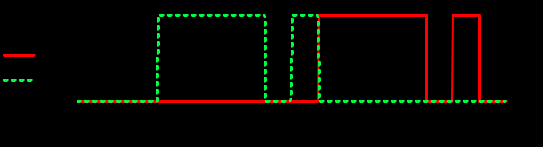  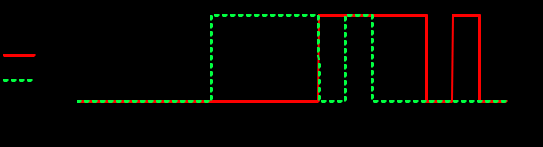 Рис 10.1. Заданный сигнал и его смещенная копия 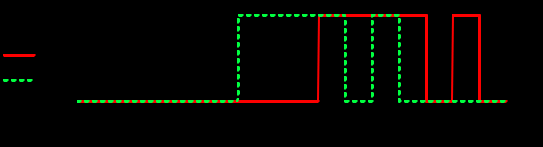  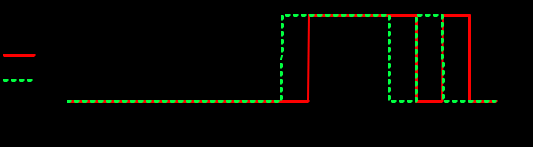 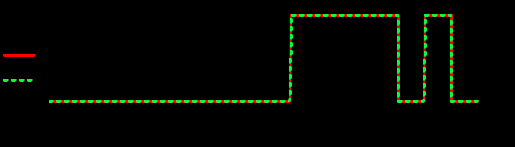 Рис 10.2. Заданный сигнал и его смещенная копия (продолжение) Исходный сигнал задан на промежутке [0, T], поэтому его автокорреляционная функция определяется как:  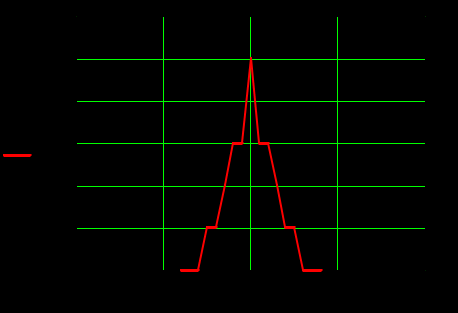 Рис 11. Автокорреляционная функция заданного сигнала U(t) Полученная автокорреляционная функция достигает максимума при  =0 и равна при этом значении аргумента энергии сигнала: =0 и равна при этом значении аргумента энергии сигнала: А также она является четной для вещественных сигналов. Определить эффективную ширину спектра, как полосу частот, содержащую 95% энергии сигнала Спектральную плотность энергии сигнала U(t) легко получить из обобщенной формулы Релея при этом получим:  Найдем 95% этой энергии:  Полосу частот, содержащую 95% энергии можно определить с помощью блока решений Given – Find в программе MathCAD.  Найти сигнал, который получается из заданного при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ (частота среза 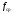 фильтра в МГц и крутизна фильтра в МГц и крутизна  ФЧХ в рад/МГц приведены в табл. 2), построить временной график полученного сигнала (для выполнения этого пункта рекомендуется использовать математическую программу MathCAD, MATLAB и т.п.) ФЧХ в рад/МГц приведены в табл. 2), построить временной график полученного сигнала (для выполнения этого пункта рекомендуется использовать математическую программу MathCAD, MATLAB и т.п.)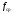 =24 МГц – частота среза фильтра согласно варианту 4; =24 МГц – частота среза фильтра согласно варианту 4;S=0.9 рад/МГц – крутизна ФЧХ фильтра согласно подварианту 1. Запишем математическую модель КЧХ фильтра с помощью функций Хэвисайда:  ; ;Здесь мы крутизну делим на 2  , а частоту умножаем на 2 , а частоту умножаем на 2 , т. к. КЧХ фильтра зависит от круговой частоты , т. к. КЧХ фильтра зависит от круговой частоты  . .Спектральная плотность выходного сигнала находится как произведение КЧХ фильтра и спектральной плотности входного:  ; ;Сигнал, который получится на выходе, вычислим по формуле: 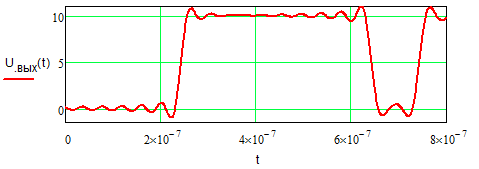 Рис 12. Временной график сигнала полученного из заданного при воздействии фильтра с прямоугольной АЧХ и линейной ФЧХ Н 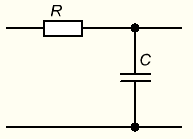 айти сигнал, который получается при воздействии заданного сигнала на RC-фильтр нижних частот с параметрами, указанными в табл. 3 ( айти сигнал, который получается при воздействии заданного сигнала на RC-фильтр нижних частот с параметрами, указанными в табл. 3 (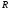 в кОм, в кОм,  в пФ), построить временной график полученного сигнала в пФ), построить временной график полученного сигналаR=0.25 кОм – согласно варианту 4; C=900 пФ – согласно подварианту 1. Рис 13. Фильтр нижних частот Фильтр нижних частот имеет импульсную характеристику:  Сигнал на выходе линейной цепи является сверткой входного сигнала и импульсной характеристики: 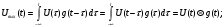 В нашем случае сигнал существует на промежутке [0,T] поэтому: 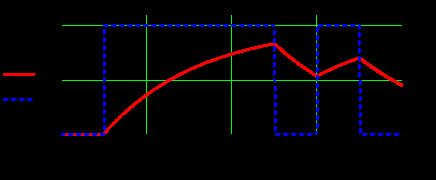  ; ;Рис 14. Временные графики выходного и входного сигналов Линейные инвариантные к сдвигу цепиЛИС-цепь определяется схемой согласно варианту (табл. 4), ее параметры ( 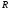 в кОм, в кОм,  в пФ, в пФ, 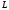 в мГн ) – согласно подварианту (табл. 5). Однотипные элементы нумеруются в соответствии с их расположением на схеме: слева направо и сверху вниз. Предполагается, что выход цепи подключен к устройству с бесконечным входным сопротивлением. в мГн ) – согласно подварианту (табл. 5). Однотипные элементы нумеруются в соответствии с их расположением на схеме: слева направо и сверху вниз. Предполагается, что выход цепи подключен к устройству с бесконечным входным сопротивлением. 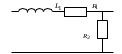 Рис 15. Заданная ЛИС цепь R1=2 кОм; R2=1 кОм; L1=1 мГн; – согласно подварианту. Требуется: Найти комплексную частотную характеристику цепи, АЧХ и ФЧХ; построить графики АЧХ и ФЧХ КЧХ линейной цепи вычисляется по формуле:  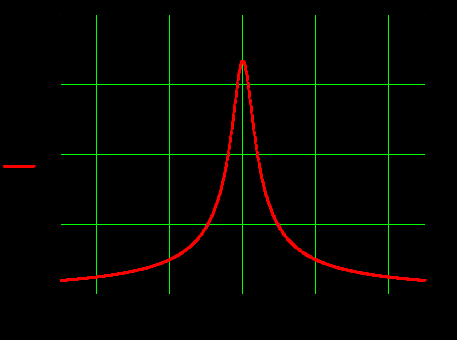 Рис 16. Амплитудно-частотная характеристика линейной цепи 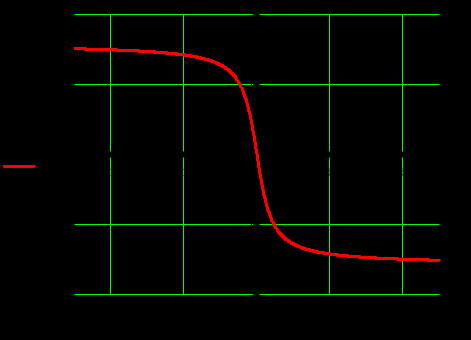 Рис 17. Фазо-частотная характеристика линейной цепи Найти импульсную и переходную характеристики, построить графики Исходная ЛИС-цепь имеет комплексную характеристику:  Заменим 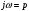 тогда: тогда: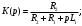 Импульсную характеристику найдем по формуле обратного преобразования Лапласа от КЧХ линейной цепи:  В нашем случае имеем: 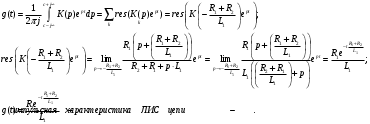  Рис 18. Импульсная характеристика линейной цепи Переходную характеристику можно найти, проинтегрировав полученную импульсную характеристику: 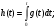 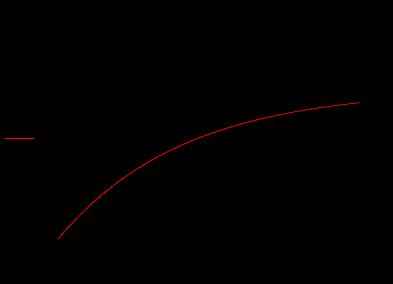 Рис 19. Переходная характеристика линейной цепи Найти отклик цепи на заданный сигнал, построить график Отклик цепи получим по ранее приведенной формуле − свертке входного сигнала и импульсной характеристики: 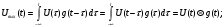  Рис 20. Временные графики выходного и входного сигналов |
