элективный курс Математика вокруг нас. эл курс матем.вокруг нас.... Симметрия вокруг нас

• Название: Симметрия вокруг нас
• Анкор: элективный курс Математика вокруг нас
• Дата: 17.11.2022
• Размер: 0.99 Mb.
• Имя файла: эл курс матем.вокруг нас....doc
• Тип: Пояснительная записка; #794918
• страница: 3 из 4

Тема: «Методы решения задач на преобразование выражений»

Перейдем теперь к рассмотрению методов использования при­веденных правил для решения некоторых видов задач на тож­дественные преобразования выражений.

2. Задачи на приведение выражений

к стандартному виду.

Для некоторых выражений с переменными в математике вво­дится понятие о стандартном виде этих выражений. Это такая форма записи выражений, которая принимается за нормальную (стандартную), и любое выражение данного типа с помощью тождественных преобразований обычно приводится к этому стан­дартному виду.

Стандартный вид установлен не для всех типов выражений. Так, для иррациональных, логарифмических и тригонометричес­ких выражений какого-то определенного стандартного вида не установлено. Укажем те типы выражений, для которых установ­лен определенный стандартный вид.

1. Одночлены. Стандартным одночленом называется такой одночлен, в котором имеется лишь один числовой множитель, стоящий на первом слева месте (числовой коэффициент), и каждое
произведение одинаковых переменных в нем представлено сте­пенью.

Например, одночлен 1,2а²в(—5ав⁴)(—aв²) после приведения к стандартному виду будет иметь такой вид: 6а⁴в⁷.

2. 
   Многочлены. Многочлен считается приведенным к стан­дартному виду, если он представляет собой сумму стандартноговида одночленов. Иногда еще требуется расположение этих од­ночленов по убывающим степеням одной из переменных. Последнеетребование, не являясь обязательным, имеет особый смысл в слу­чае, когда многочлен есть выражение с одной переменной.
   
3. 
   Целые рациональные выражения. Любое целое
   рациональное выражение можно преобразовать в тождественный
   ему многочлен стандартного вида.
   
4. 
   Дроби (дробные выражения). За стандартный вид дроб­ного выражения принимается несократимая дробь, числитель изнаменатель которой представляют собой многочлены стандарт­ного вида.
   
5. 
   Рациональные выражения. Любое рациональное
   выражение, в котором переменные связаны действием деления,
   всегда можно преобразовать в тождественно равную ему дробь
   стандартного вида.
   

Рассмотрим несколько задач на приведение выражений к стандартному виду.

Задача 1. Представить выражение



в виде многочлена стандартного вида.

Решение. Заданное выражение есть целое рациональное выражение. Для того чтобы представить его в виде многочлена стандартного вида, нужно: 1) раскрыть все скобки; 2) все одно­члены привести к стандартному виду; 3) привести подобные одночлены; 4) если нужно, расположить все одночлены в каком-то порядке (например, по убывающим степеням одной из пере­менных).

Проделаем все эти преобразования в заданном выражении.

Для раскрытия скобок используется распределительный закон 1.5 и правила раскрытия скобок П.З и II.4. Однако в данном случае сразу применить правило 1.5 нельзя, ибо это правило позволяет преобразовывать выражения вида (а+в)с, а в данной задаче мы имеем выражения вида с (а + в). Поэтому предвари­тельно нужно воспользоваться переместительным законом умно­жения 1.3 и в каждом из трех слагаемых мысленно переставить сомножители (т.е. 5aв(aв—в²) представить как (aв—в²)5ав, 7а²(а²—в²) представить в виде (а²—в²)7а²и 5в²(а²—aв) — в виде (а²—ав)5в², а уже затем применить распределительный закон 1.5).

Теперь о расстановке знаков при раскрытии скобок. Можно поступать двояким образом. Можно рассматривать знак перед одночленом, как знак, относящийся к его коэффициенту, и тогда всюду будем иметь сумму одночленов. В данном выражении это означает представление его в таком виде:

5ав (aв + (— в²)) + (—7а²) (а² + (— в²)) + 5в² (а² + (— aв)).

Тогда при раскрытии скобок знаки коэффициентов произведе­ний определяются по известным правилам умножения положи­тельных и отрицательных чисел.

Но можно делать иначе. А именно рассматривать имеющиеся знаки перед одночленами как знаки действий, а сами коэффи­циенты одночленов считать положительными. Тогда при раскры­тии скобок следует использовать распределительный закон относительно вычитания (в приведенном списке правил он не указан): (а—в)с = ас—вс. И кроме того, использовать правила раскрытия скобок П.З и II.4. Тогда последовательное преобра­зование заданного выражения будет таким (справа в скобках указаны используемые при каждом шаге-преобразовании пра­вила тождественных преобразований):

5ав (ав—в²)—7а² (а²—в²) + 5в² (a²—ab) = (1.3)

= (ав —в²)(5ав) — (а²—в²) (7а²) + (а² —ав)(5в²)= (1.5)

= (ab 5ав—в² 5ав) — (а² 7а²—в² 7 а²) + (а² 5в²—ав 5в²) =

(1.3; 1.4; V.6)

= (5а² в²—5ав³)—(7а⁴—7а²в²) + (5а²в²—5ав³)= (П.З; II.4) = 5а²в²—5ав³—7а⁴ + 7а^гв² + 5а²в²—5ав³.

Теперь в полученном выражении нужно привести подобные члены. Это производится на основе того же распределительного закона, но читать его надо справа налево. Получим:

5а²в²—5ав³—7а⁴ + 7а²в² + 5а²в²—5ав³ = (5 + 7 + 5) a²в² + (—5—5) aв³—7а⁴ = 17a²в² — 10ab³—7а⁴.

В полученном многочлене можно расположить члены по убы­вающим степеням переменной, например а, тогда окончательно получим:

—7а⁴+17а²в²— 10ав³.
Это и будет стандартный вид заданного выражения.

3 а д а ч а 2. Преобразовать выражение

в дробь.

Решение. Требование этой задачи надо понимать так, что заданное рациональное выражение нужно преобразовать в стан­дартный вид дроби. Так как заданное выражение представляет собой произведение двух рациональных выражений, то каждое из них надо предварительно представить в виде стандартной дроби, а затем полученные дроби перемножить и, если можно, результат представить в стандартной форме дроби.

Проделаем все это, записывая справа в скобках используемые правила тождественных преобразований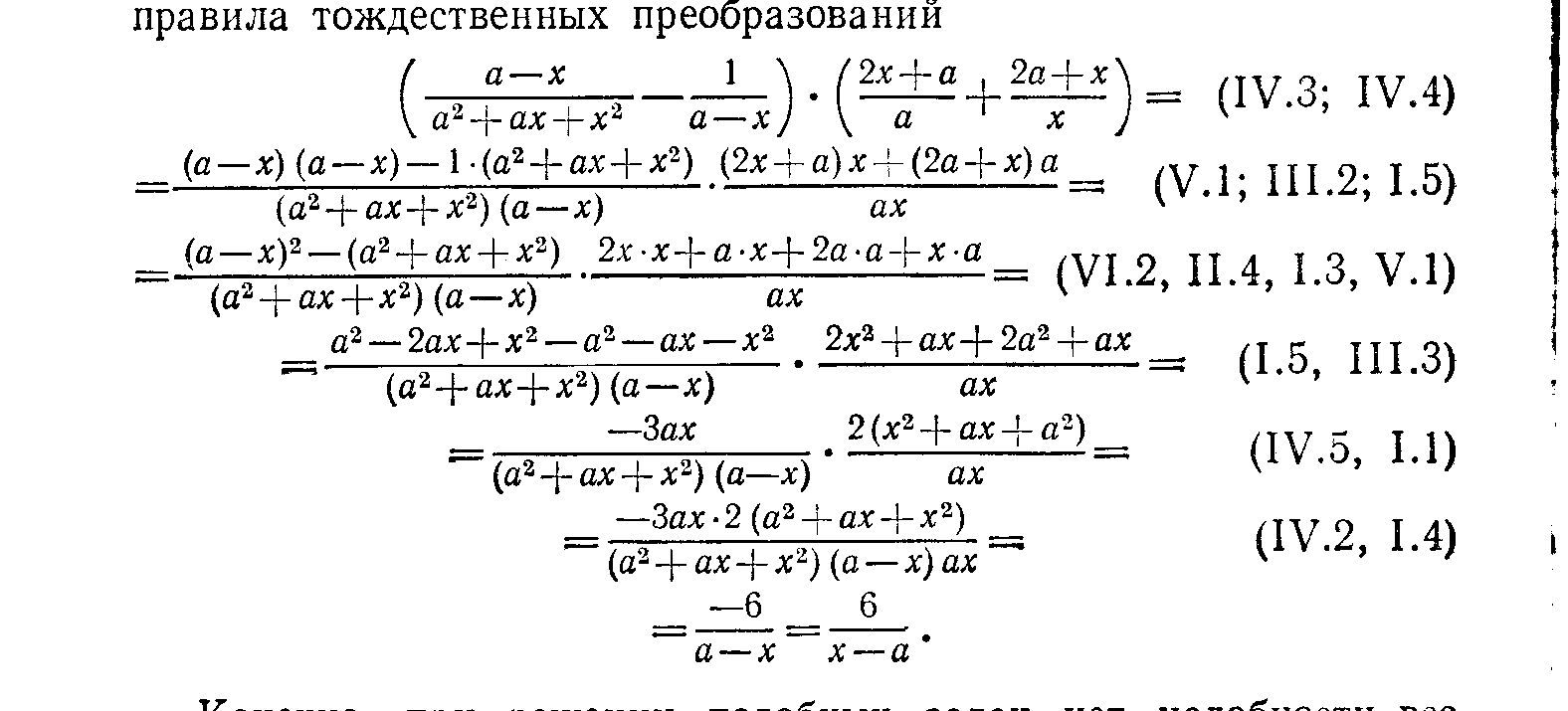



Конечно, при решении подобных задач нет надобности все время делать ссылки на те правила тождественных преобразова­ний, которые используются в решении. Это обычно не требуется. Но если вы хотите сознательно овладеть такими преобразованиями с полным пониманием сущности каждого шага, то нужно хотя бы несколько задач решить так, как было проделано выше, т. е. с указанием всех используемых на каждом шаге правил тож­дественных преобразований.

Задание 1

Решите задачи, указывая, как это было сделано выше, все правила тож­дественных преобразований, которые вы использовали в решении.

1. 
   Преобразовать выражение (2x — 5y)³-—x(6x--5y)^zк стандартному виду.
   

1.2. Представить в стандартной форме дроби выражение

.

1.3. На основе каких правил тождественных преобразований произведен переход от дроби к дроби в решении задачи 2?

3. Задачи на упрощение выражений

Задачи на упрощение выражений с переменными встречаются очень часто, при этом в отличие от задач на приведение выра­жений к стандартному виду упрощать приходится любые выра­жения, а не только рациональные. Но в то же время эти задачи менее определенные, ибо не всегда ясно, упрощено ли уже вы­ражение и нельзя ли его еще упростить.

Характерный пример: Упростить выражение .

При решении этой задачи одни учащиеся получили ответ:

4 cos2xcos х, а другие: 2 (cosx+cos3x). Оба эти ответа верны, но какой из них лучше, вряд ли можно сказать.

Однако в большинстве случаев упрощение выражений является достаточно определенным преобразованием. Смысл его состоит в том, чтобы, пользуясь приведенными выше правилами и фор­мулами тождественных преобразований, представить заданное выражение в более простой, компактной форме.

Из-за некоторой неопределенности понятия „простая форма" нет возможности указать какое-либо общее правило для решения задач этого типа, но для отдельных видов выражений можно достаточно определенно это сделать. Мы укажем эти правила на примерах упрощения разных выражений.

Задача 3. Упростить выражение (2-в)(1+2в)+(1+в)(в²+3в)

Решение. Заданное выражение есть целое рациональное выражение. Для его упрощения следует: 1) раскрыть скобки (т. е. выполнить все указанные действия) и 2) привести подобные члены. Иными словами, надо данное выражение привести к стан­дартному виду многочлена.

В данном случае получим:

(2-в)(1+2в)+(1+в)(в²+3в)=2+4в-в-2в²+в²-3в+в³-3в²=в³-4в²+2.

Задача 4. Упростить выражение (2р-3)(4р²+6р+9)+(р+3)(р²-3р+9).

Решение. Так как заданное выражение есть целое рацио­нальное, то можно поступить так же, как в предыдущей задаче. Но если внимательно рассмотреть условие, то замечаем, что к каждому из слагаемых применимы тождества VI.5 и VI.4, читая их справа налево, получим:

(2р-3)(4р²+6р+9)+(р+3)(р²-3р+9)=((2р)³-3³)+(р³+3³)=8р³-27+р³+27=9р³.

Задача 5. Упростить выражение .

Решение. Данное выражение является рациональным, поэ­тому его упрощение сводится обычно к приведению к стандарт­ному виду. Сначала нужно сложить все входящие в это выраже­ние дроби. Следовательно, нужно найти общий знаменатель этих дробей, а для этого знаменатели надо разложить на множители. Замечаем, что к знаменателю первой дроби применимо правило разложения разности квадратов, а к знаменателям второй и третьей дробей — правило вынесения общего множителя за скобки. Обо­значив для простоты заданное выражение буквой М (так мы будем делать и в последующем), получим:
М= .
Обнаруживается, что вторую дробь можно сократить на у. Кроме того, замечаем, что в знаменателе первой дроби имеется множитель х—5у, а знаменатель второй дроби (после сокраще­ния) равен 5у—х, т.е. отличается лишь знаком. Поэтому члены второй дроби умножим на —1, получим: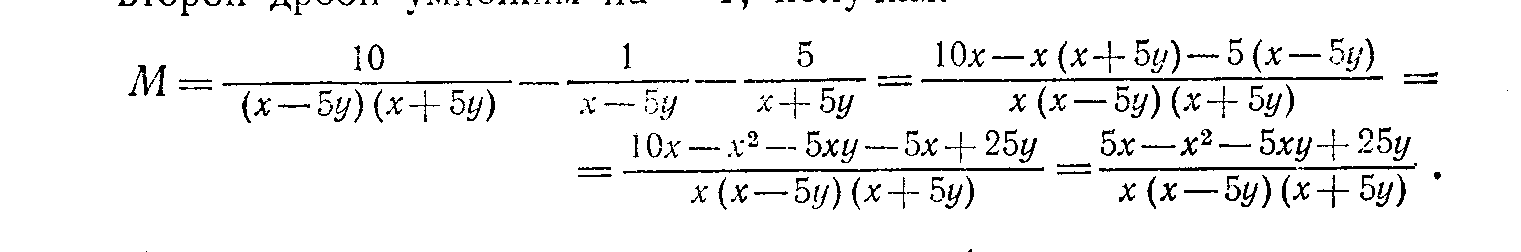


Чтобы проверить, нельзя ли сократить (и следовательно, упро­стить) эту дробь, нужно разложить на множители числитель. В данном случае это легко сделать, сгруппировав первое и чет­вертое слагаемое и второе и третье. Получим: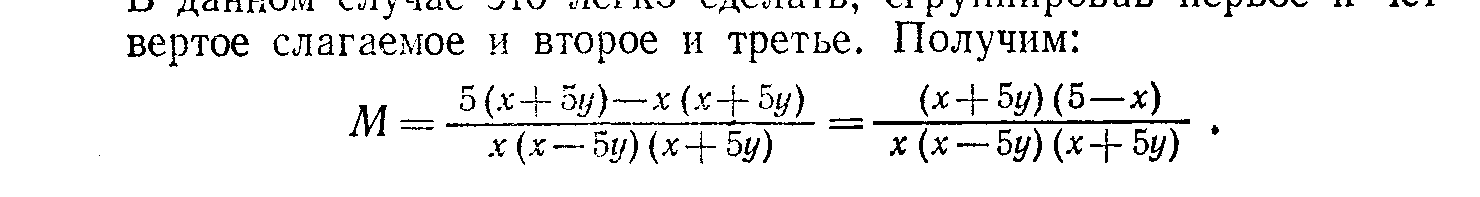

Видим, что дробь действительно можно сократить, после чего

получаем ответ М =

Задача 6. Упростить выражение .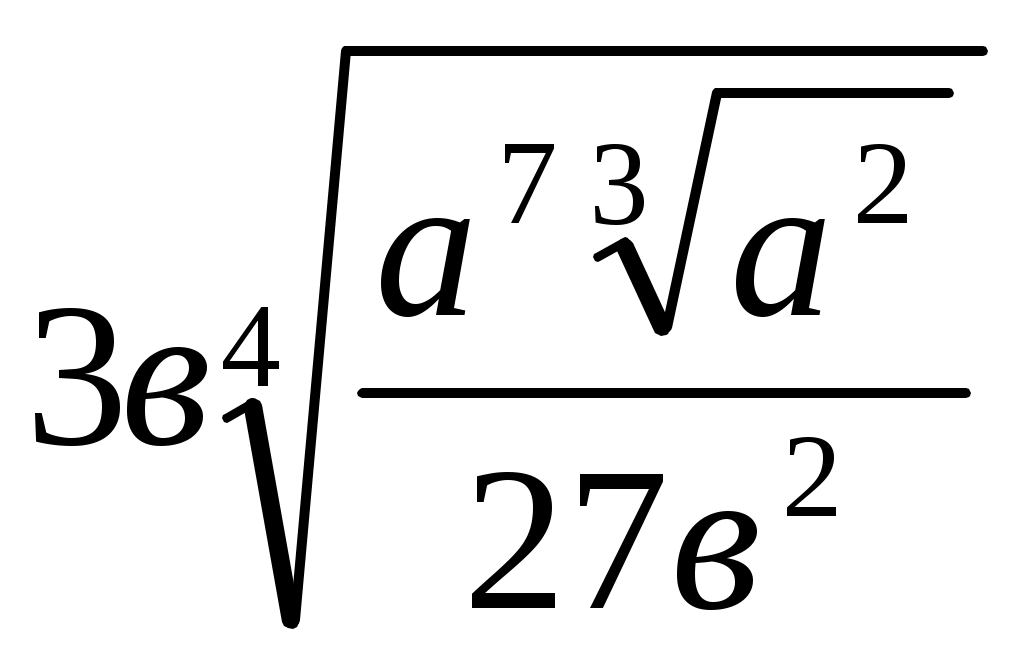

Решение. Заданное выражение есть одночленный корень. Его упрощение обычно сводится к следующим операциям:

1. 
   произвести все указанные в выражении действия (возведение в степень, извлечение корня из корня и др.);
   
2. 
   освободиться от дроби под знаком корня;
   
3. 
   вынести за знак корня все рациональные множители;
   
4. 
   сократить показатель корня с показателями подкоренного
   выражения.
   

Однако предварительно нужно установить условия, при кото­рых данное выражение имеет смысл, т. е. найти область его оп­ределения. Так как имеем арифметический корень, то подкоренное выражение должно быть неотрицательным, а поэтому а⁷, а следо­вательно, и а 0(1); в², стоящее в знаменателе, должно быть отлично от нуля, значит, в 0(2).

Преобразование корня в данном случае удобнее начать со вто­рой операции, а именно освободиться от дроби под знаком корня. Для этого умножим числитель и знаменатель подкоренного выра­жения на такой множитель, чтобы в знаменателе получить про­изведение, из которого целиком извлекается корень. Очевидно, что нужно умножить на 3в², получим М= .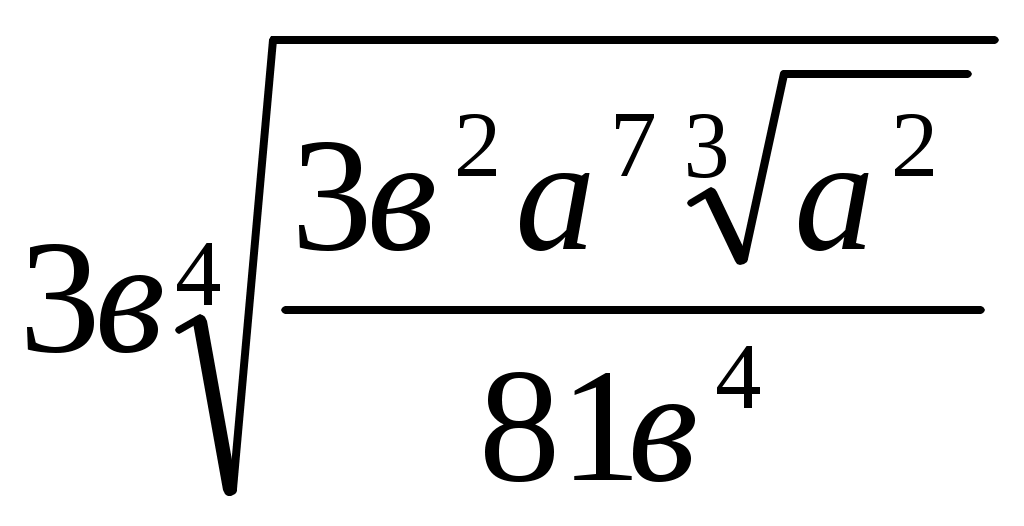

Извлекая корень 4-й степени из знаменателя, мы получим 3 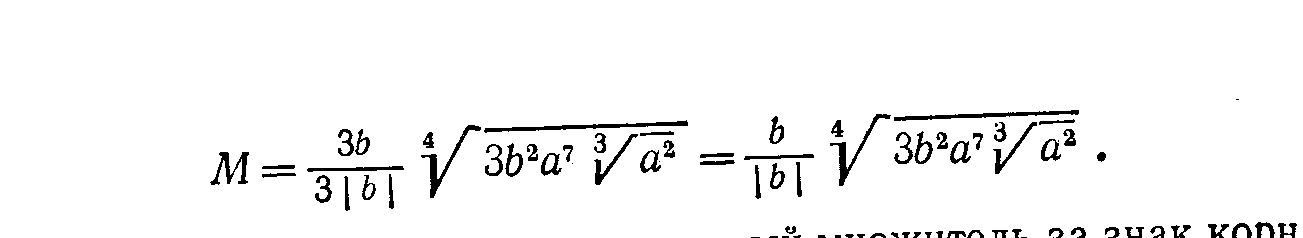, ибо согласно условию (2) знак в неизвестен, а в таком случае по определению арифметического корня . Получим:



Теперь можно вывести рациональный множитель за знак корня на основе правила VII.6. Для этого смотрим, показатель какой переменной под корнем не меньше показателя корня. Видим, что показатель а равен 7 > 4. Значит, можно вынести за знак кор­ня а. Учитывая условие (1), получим: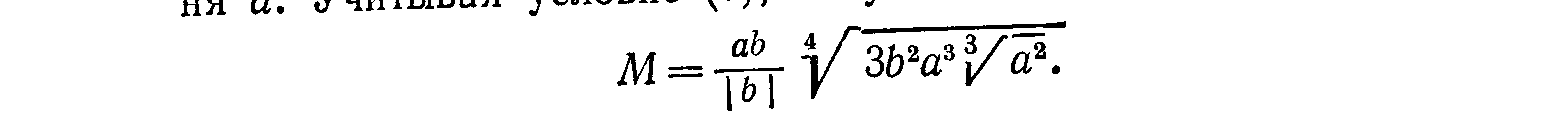



Для того чтобы выполнить извлечение корня из корня, можно поступить двояко. Можно сначала множитель, стоящий перед внутренним корнем, подвести под знак этого корня, а затем уже извлечь корень из корня:

Можно сделать иначе, а именно сначала извлечь внешний корень из произведения, а затем полученные результаты пере­множить, приведя их предварительно к общему показателю: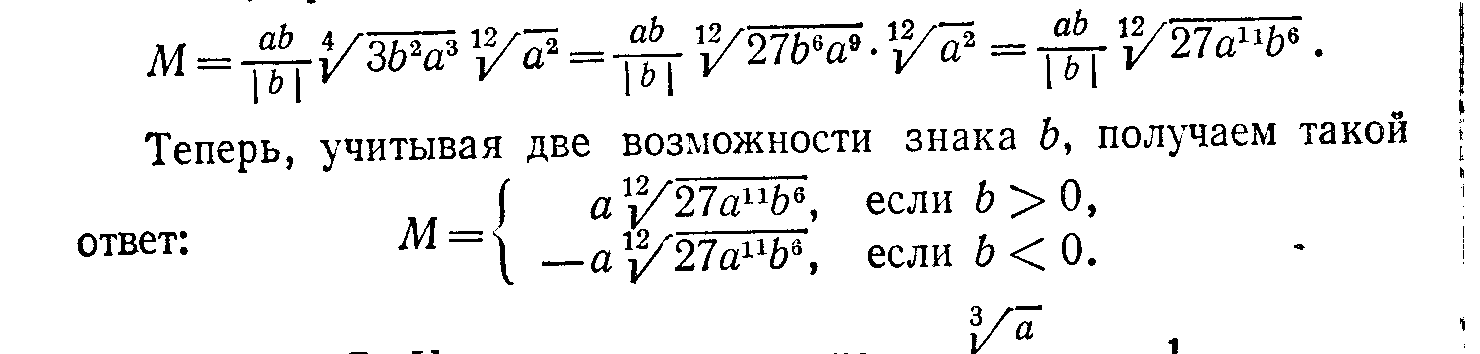

Задача 7, Упростить выражение .

Решение. Сначала находим область определения заданного выражения. Очевидно, она определяется так, чтобы знаменатель имеющейся дроби не был равен нулю. Это будет при условии: а в.

Теперь выполним указанные действия, т. е. приведем выражение к виду дроби: М = .

Дальнейшее упрощение этого выражения может заключаться в избавлении от корней в знаменателе (как говорят: избавиться от иррациональности в знаменателе дроби). Так как в знамена­теле кубические корни, то, чтобы получить рациональное выра­жение, надо каждый из этих корней возвести в куб, т. е. надо получить разность кубов этих корней. Для этого воспользуемся тождеством VI.5 и умножим числитель и знаменатель полученной дроби на

.