элективный курс Математика вокруг нас. эл курс матем.вокруг нас.... Симметрия вокруг нас

Название	Симметрия вокруг нас
Анкор	элективный курс Математика вокруг нас
Дата	17.11.2022
Размер	0.99 Mb.
Формат файла
Имя файла	эл курс матем.вокруг нас....doc
Тип	Пояснительная записка #794918
страница	4 из 4

1 2 3 4

Задание 2.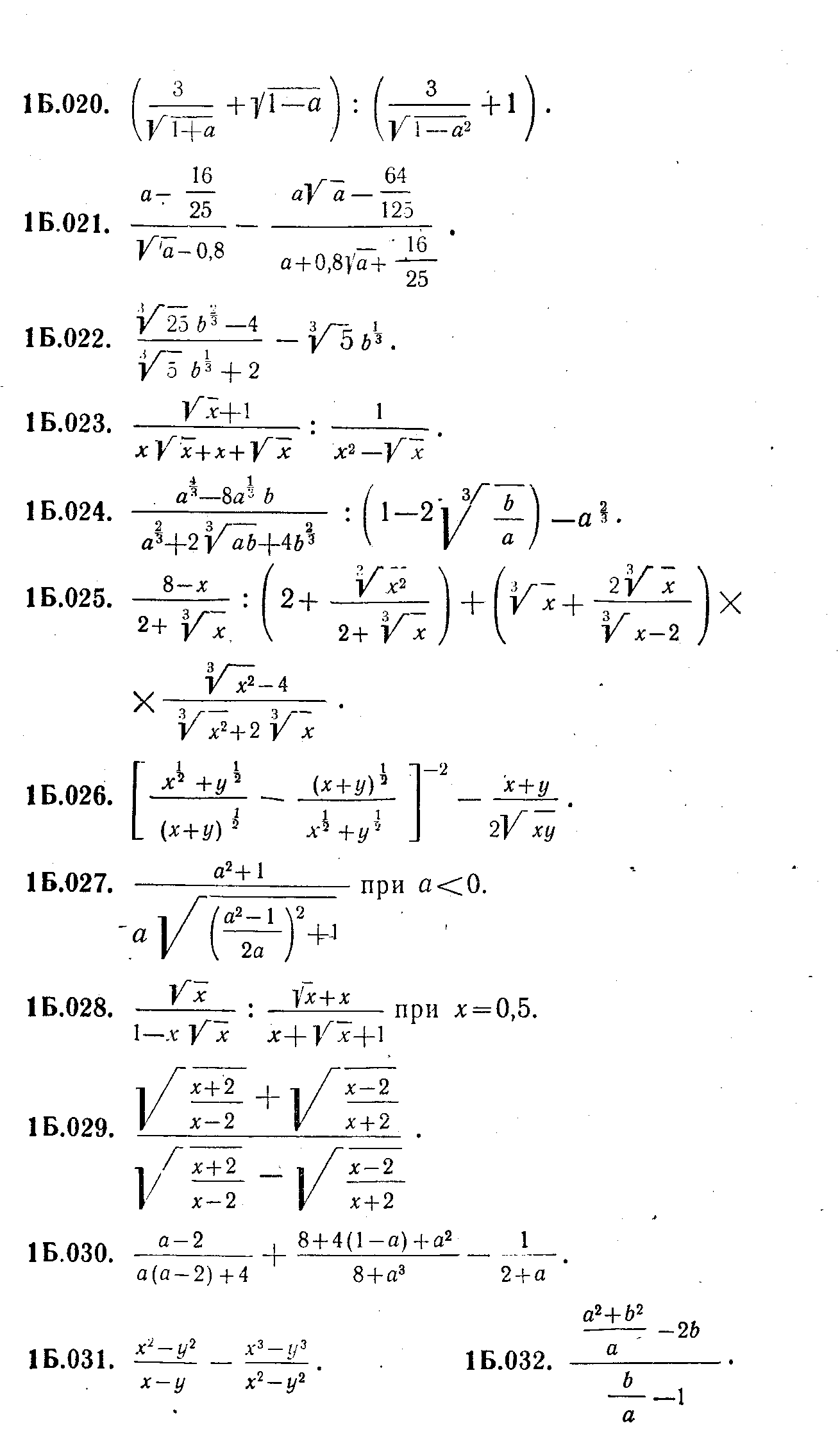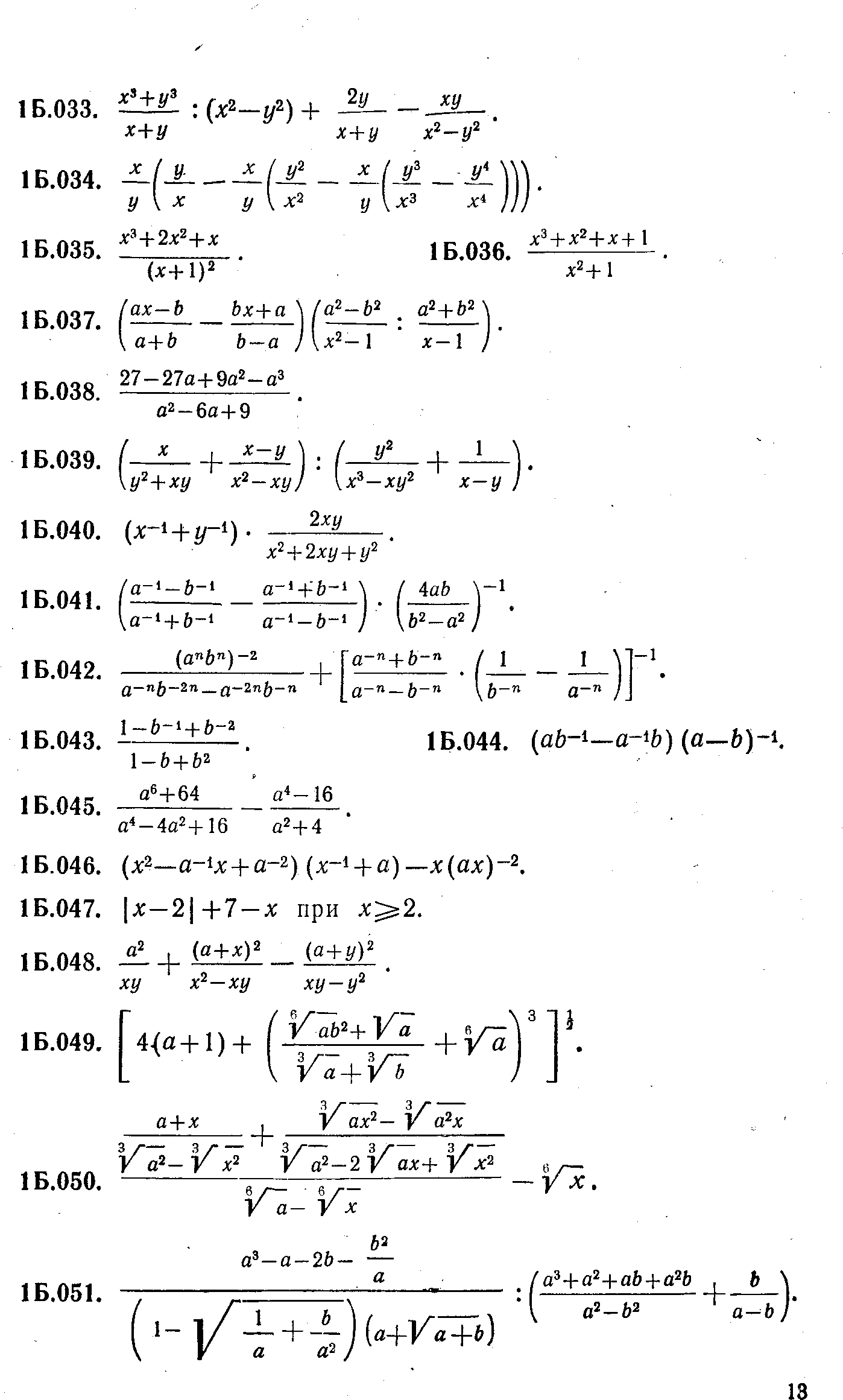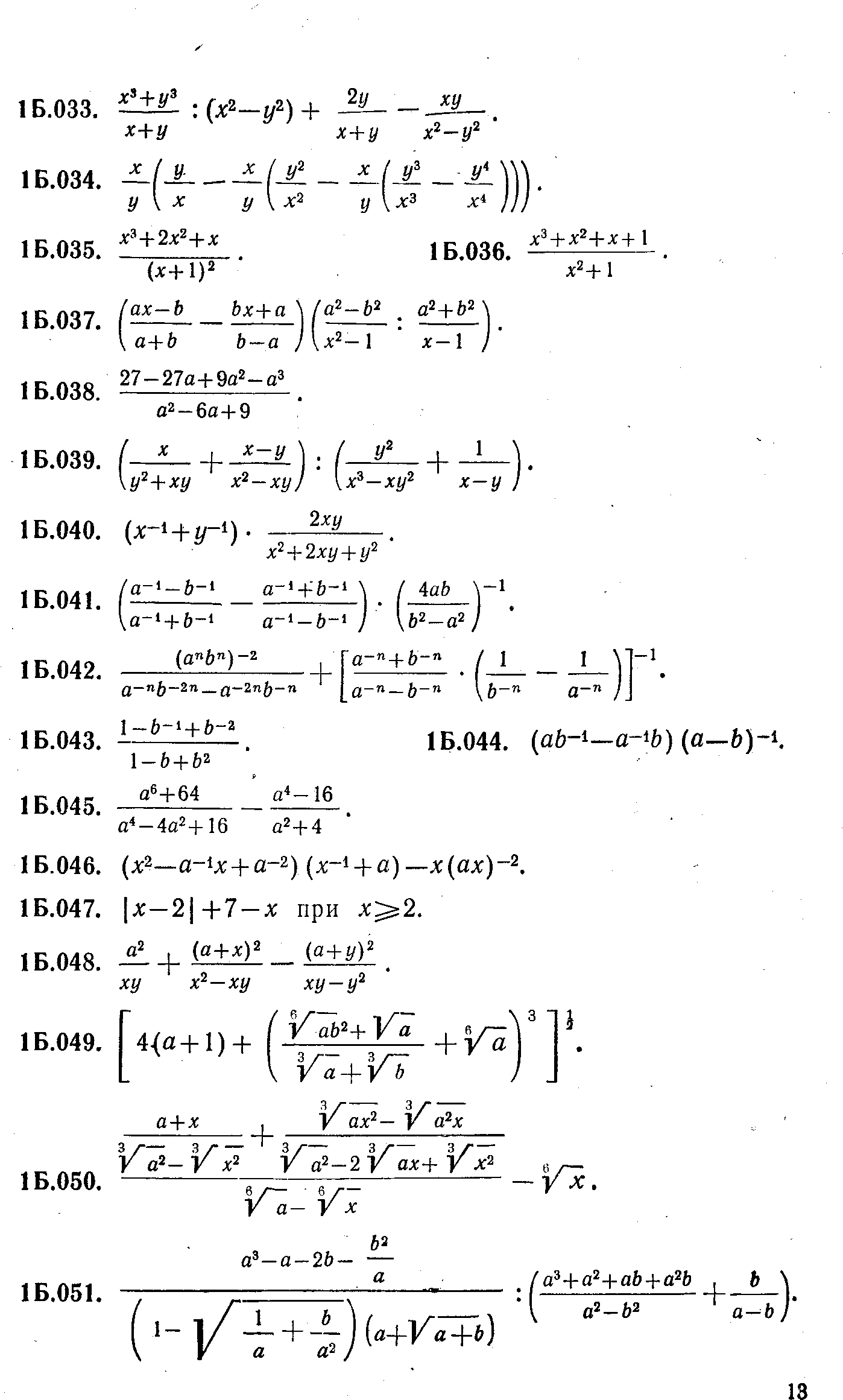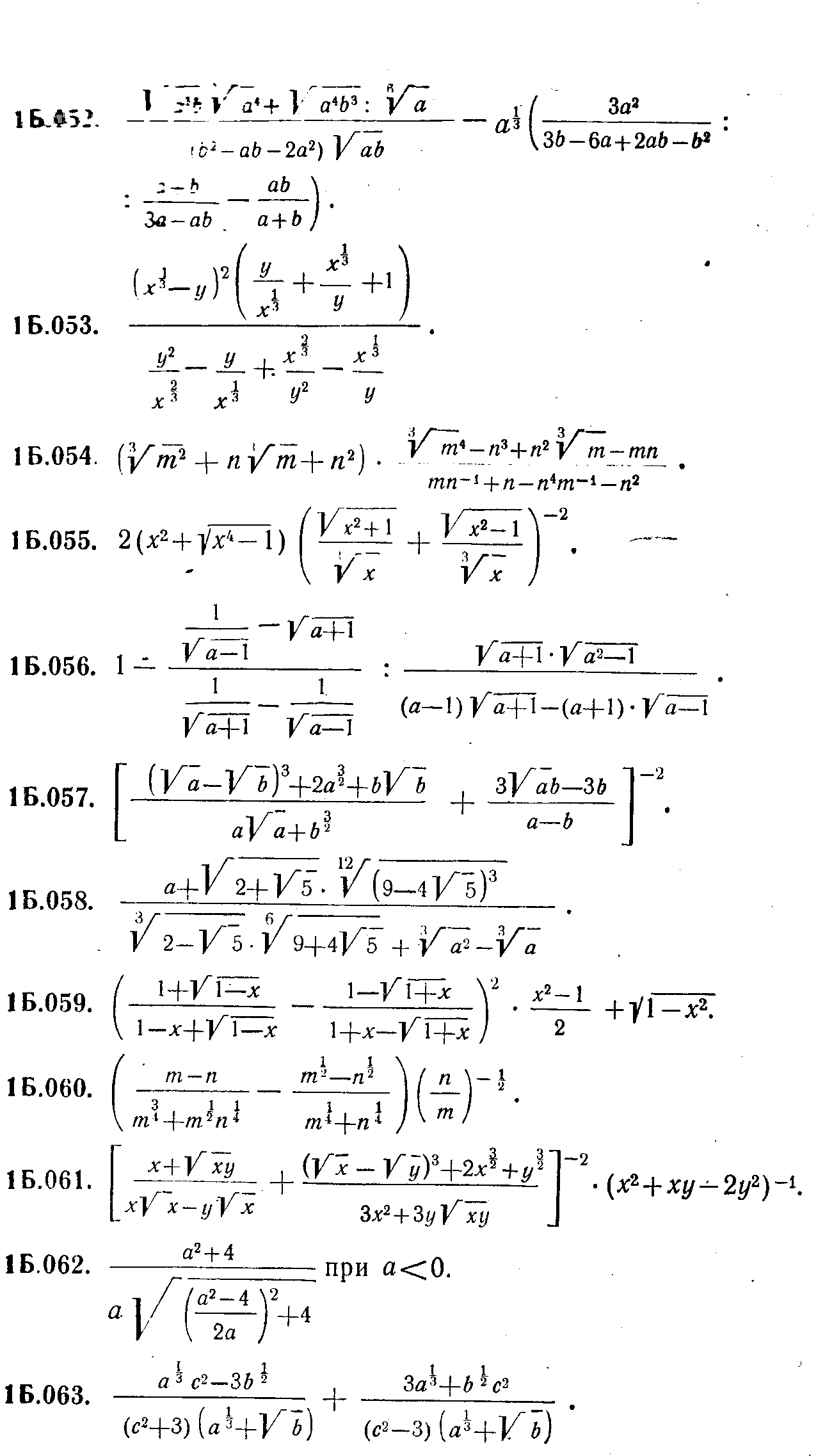

4. Разложение на множители.

С необходимостью разложения выражений на множители вы уже встречались при приведении дробей к общему знаменателю, при сокращении дробей. Это же преобразование широко используется при решении уравнений и неравенств. Поэтому научиться раскладывать некоторые простейшие выражения на множители крайне важно.

В общем виде задача разложения на множители многочленов, уже не говоря о более сложных выражениях, средствами школьной математики неразрешима. Но в тех простейших случаях, которые встречаются в школьной и экзаменационной практике, достаточно тех методов, которые изучаются в VII классе (вынесение общего множителя за скобки, применение тождеств сокращенного умножения, метод группировки).

Покажем, как следует использовать эти методы для решения ;адач разложения на множители различных выражений.
Задача 9. Разложить на множители многочлен 6х³у+3х²у²-3ху³.

Решение. Разложение на множители многочленов производится с помощью следующих операций в таком порядке:

Вынесение общего множителя за скобки.' Проверяем, неимеют ли все одночлены, входящие в многочлен, общего множителя. Если да, то выносим его за скобки, если нет, то переходим
к следующей операции.
Применение тождеств сокращенного умножения. Проверяем
не представляет ли заданный многочлен такое выражение, к которому непосредственно применимо одно из тождеств сокращенного умножения (разность квадратов, квадрат или куб двучлена,разность или сумма кубов). Если да, то применяем это тождество,
если нет, то переходим к следующей операции.
Группировка членов. Разбиваем многочлен на несколько
(два или более групп) и к каждой из них пытаемся применить
первые две операции.

Применим эту последовательность операций к заданному многочлену.

Все члены многочлена М имеют общий множитель Зху. Выносим его за скобки. Получим: М = 3ху (2х²+ху—у²).

Теперь попытаемся разложить на множители многочлен К, стоящий в скобках. Очевидно, что к нему первые две операции (вынесение общего множителя за скобки и применение тождеств сокращенного умножения) неприменимы. Попытаемся тогда произвести группировку членов. Так как многочлен можно разбить минимум на два многочлена и в каждом из них должно быть не менее двух членов, то, для того чтобы можно было произвести группировку, в данном многочлене должно быть не менее четырех членов. А в многочлене К имеется всего три члена. В таком случае разобьем один из членов на два. Удобнее это сделать с первым членом. Тогда многочлен К принимает такой вид:

К=х²+х²+ху-у²

Группировка его членов возможна таким образом:

К= (х²-у²)+(х²+ху).

Видим, что первая группа членов представляет собой разность квадратов и, следовательно, к ней применимо соответствующее тождество, а ко второй группе применима операция вынесения общего множителя х за скобки. Получим: К= (х-у)(х+у)+х(х+у).

Рассматривая теперь полученные два произведения, видим, что они содержат общий множитель (х+у). Выносим его за скобки:

К=(х+у) (х—у+х) = (х+у) (2х—у).

Тогда окончательно получим: M = 3xy(x-\-y)(2x-y).

Задача 11, Разложить на множители выражение

(y-z)³+(z-x)³+(x-y)³.

Решение. При решении этой задачи можно поступить двояким образом:

1. Можно сначала заданное выражение преобразовать в многочлен стандартного вида, а уже затем попытаться разложить его на множители.

Применяя тождество VI.3 (куб двучлена) и приведение подобных членов, получим:

М=y³—3y²z+ Зуz²—z³+z³—3z²x+3zx²—x³+ х³—Зх²у+Зху²—у³=3(-y²z+yz²-z²x+x²z-x²y+xy²)

Сгруппируем члены многочлена, стоящего в скобках, как noказано, и применим к этим группам операции вынесения общего множителя за скобки и тождество разность квадратов: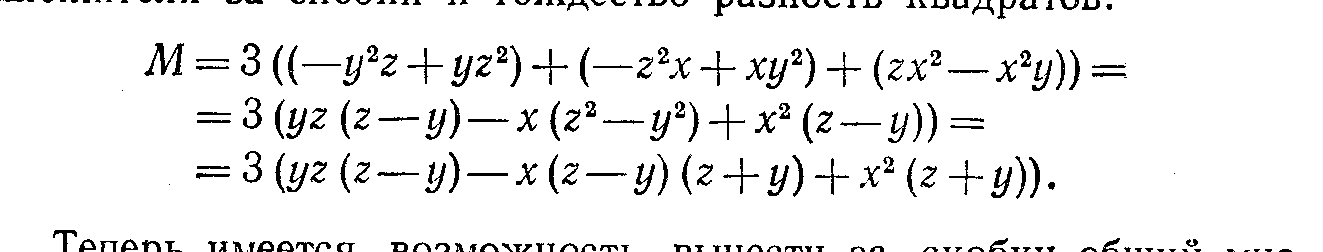

Теперь имеется возможность вынести за скобки общий множитель (z-y):

М= 3(z-y)(yz-x(z+y)+x²)=3(z-y)(yz-xz-xy+x²)/

В многочлене, стоящем во вторых скобках, произведем группировку членов, а затем операцию вынесения общего множителя скобки:

М = 3 (z—у) ((yz—xz)—(ху-х²)) =

= 3 (z—у) (z({у—х)—х(у—х)) = 3(z—у) (у-х) (z-x).

2. Можно же не преобразовывать заданное выражение к виду многочлена, а применить сразу операции по разложению на множители. В данном случае первые два слагаемых можно рассматривать как сумму кубов выражений (у—z) и (z—х), а поэтому к ним применить соответствующее тождество. Получим: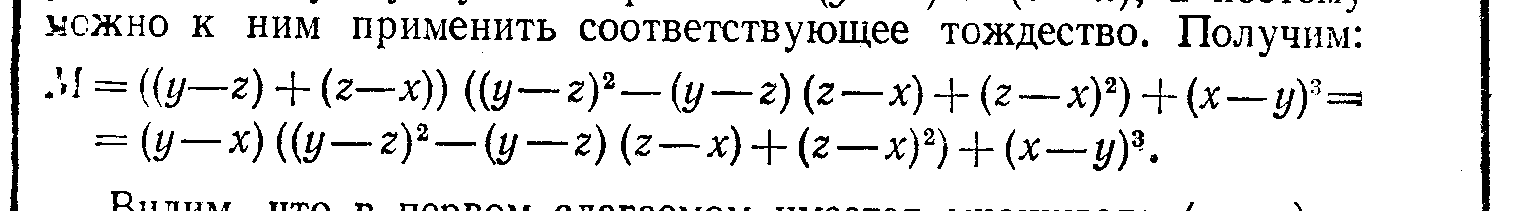

Видим, что в первом слагаемом имеется множитель (у—х), а во втором (х—у). Тогда, изменив знак второго слагаемого, получим возможность вынести за общие скобки (у—х):

М = (у—х) ((y—z)²—(y—z) (z—х) + (z—х)²—(у—х)²). (1)

В выражении К, стоящем во вторых скобках, произведем группировку членов по два по порядку и в первой группе вынесем за скобки (y—z), ко второй группе применим тождеств разность квадратов: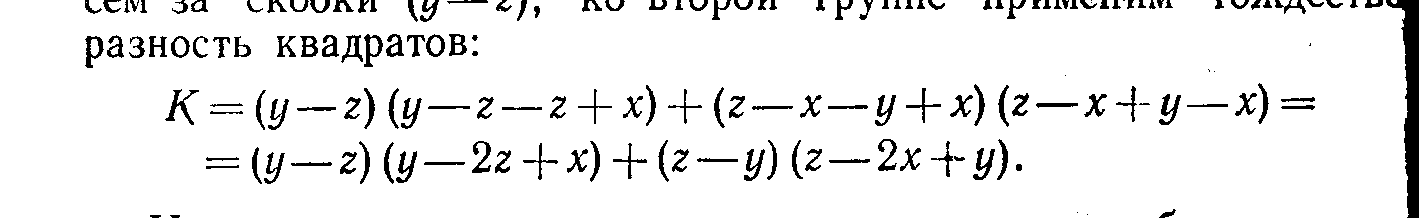

Изменим знак первого слагаемого, для того чтобы получит общий множитель (г—у), который вынесем за общие скобки:

K = (z—y)(—y + 2z—x + z—2x + y)=.(z—y)(3z — 3x) = = 3(z-y)(z-x).

Подставляя К в равенство (1), получим окончательно;

M = 3(y—x)(z—y)(z—x).

Задача 12. Разложить на множители

4 (sin⁴ х + cos⁴ x) — 4 (sin⁶ x+ cos⁶ x) —sin² 4x.

Решение. Разложение тригонометрических выражений на множители производится с помощью тех же операций, что и разложение рациональных выражений. Но естественно, что при этом используются формулы преобразований тригонометрических выражений.

В заданном выражении общих множителей нет, а вот тождество сокращенного умножения можно применить к сумме sin⁶ x + cos⁶x, рассматривая ее как сумму кубов sin² х и cos²х.

Получим: М=4 (sin⁴х+cos⁴ x) — 4 (sin² x + cos² x)

(sin⁴ x — sin² x cos²х + cos⁴х)—sin² 4х.\

На основе формулы Х.1 заменяем sin²х+cos²х единицей.
Раскрыв затем скобки и сделав приведение подобных членов
получим: М = 4 sin² xcos² х—sin² 4х.

4sin²xcos²xнапоминает формулу синуса двойного угла. Используя ее, получим: M = sin²2х:—sin²4x.

Дальше можно действовать по-разному. Можно применить тождество разность квадратов, а затем формулы суммы и разности синусов. А можно сначала применить формулы понижения степени, а уже затем формулу разности косинусов. Получим: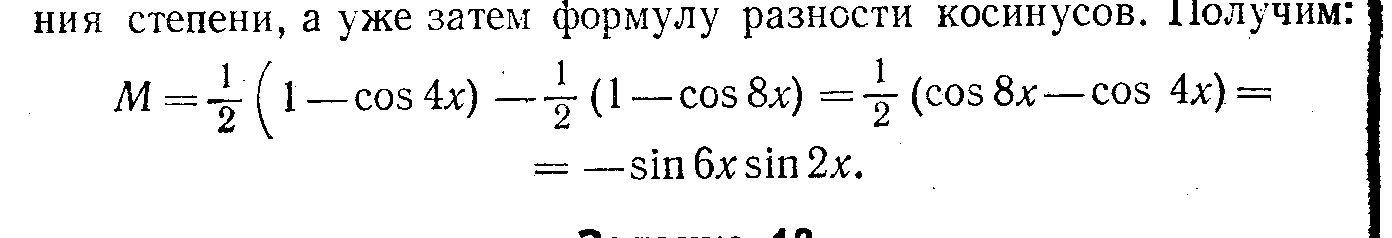

Задание 3.

Разложите на множители приведенные ниже выражения, указывая каждый раз, какие операции и формулы вы использовали в решении.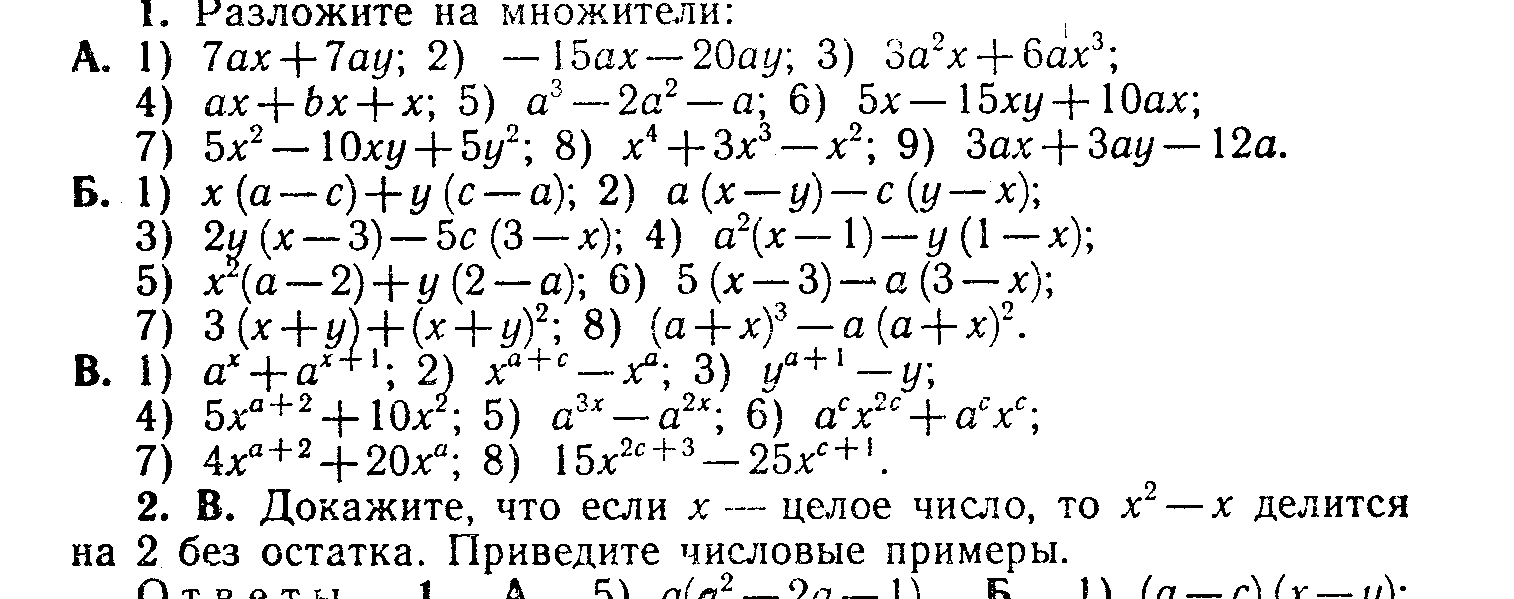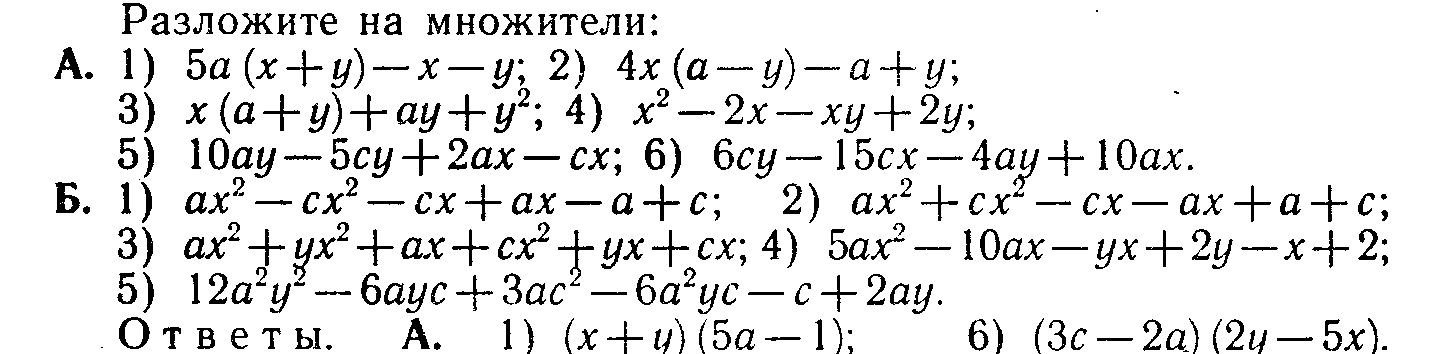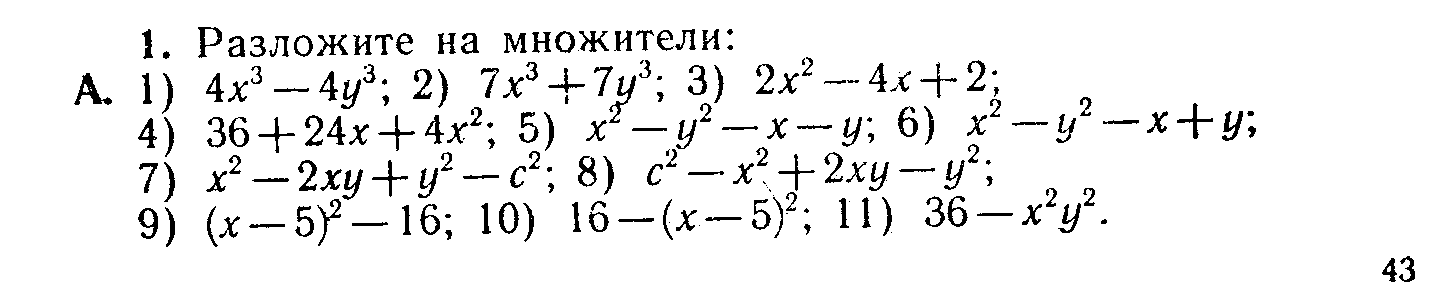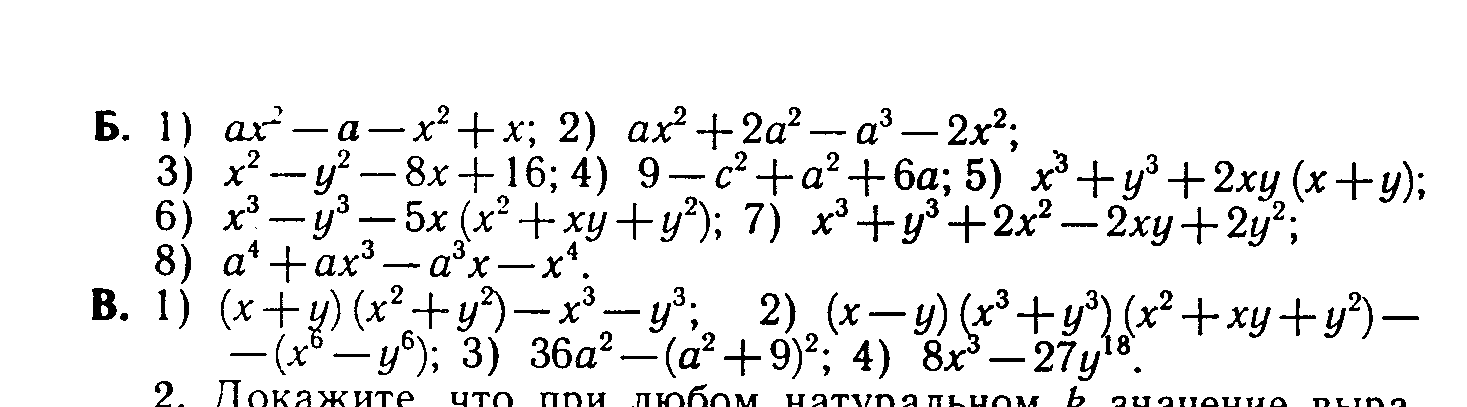

ЛИТЕРАТУРА

Литература для учителя.

Никольский, С. Н., Потапов, М. К., Решетников, Н. Н. Алгебра в 7 классе: методические материалы. — М.: Просвещение, 2002.
Барабанов, О. О. Задачи на проценты как проблемы словоупотребления // Математика в школе. - 2003. - № 5. - С. 50-59.
Башарин, Г. П. Начала финансовой математики. - М., 1997.
Башарин, Г. П. Элементы финансовой математики. - М.: Математика (приложение к газете «Первое сентября»). - № 27. - 1995.
Вигдорчик, Е., Нежданова, Т. Элементарная математика в экономике и бизнесе. - М., 1997.
Водинчар, М. И., Лайкова, Г. А., Рябова, Ю. К. Решение задач на смеси, растворы и сплавы методом уравнений // Математика в школе. -2001.-№4.
Глейзер, Г. И. История математики в школе (4-6 кл.): пособие для учителей.-М,.: Просвещение, 1981.

8. Дорофеев, Г. В., Седова, Е. А. Процентные вычисления. 10-11 классы: учеб.-метод, пособие. - М.: Дрофа, 2003. - 144 с.

9.Канашева, Н. А. О решении задач на проценты // Математика в школе. -№ 5. -1995. - С. 24.

Левитас, Г. Г. Об изучении процентов в 5 классе // Математика в школе. -№4. - 1991.-С. 39.
Липсиц, И. В. Экономика без тайн. -М.: Вита-Пресс, 1994.
Лурье, М. В., Александров, Б. И. Задачи на составление уравнений. - М.: Наука, 1990.
Макконелл, К. Р., Брюс, С. Л. Экономика. - Т.1, 2. - М.:
Республика, 1993.
Рязановский, А. Р. Задачи на части и проценты // Математика в школе. -№ 1.-1992.-С. 18.
Саранцев, Г. И. Упражнения в обучении математике. (Библиотека учителя математики). - М.: Просвещение, 1995. - 240 с.
Симонов, А. С. Проценты и банковские расчеты // Математика в школе. - 1998. -№4.
Симонов, А. С. Сегодняшняя стоимость завтрашних платежей // Математика в школе. - 1998. -№ 6.

Литература для учащихся.

Виленкин, Н. Л. За страницами учебника математики. - М.: Просвещение, 1989.-С. 73.
Виленкин, Н. Л., Жохов, В. П., Чесноков, А. С, Шварцбурд, С. И. Математика 6. - М.: Дрофа, 2000.
Денищева, Л. О., Бойченко, Е. М., Глазков, Ю. А. и др. Готовимся к единому государственному экзамену. Математика. - М.: Дрофа, 2003.-120 с.
Егерев, В. К. и др. Сборник задач по математике для поступающих во втузы / под ред. М. И. Сканави. - М.: Высшая школа, 1988.

5. Литцман, Е. Великаны и карлики в мире чисел. - М., 1959.Математика: Алгебра. Функции. Анализ данных. 8 класс: учеб. для общеобраз. учеб. заведений / под ред. Г. В. Дорофеева. - 2-е изд., стереотипное. - М: Дрофа, 2000. - 304 с.

Математика: Алгебра. Функции. Анализ данных. 9 кл: учебник для общеобраз. учеб. заведений / под ред. Г. В. Дорофеева. - М: Дрофа, 2000. - Глава IV.
Перельман, Я. И. Занимательная алгебра. - М., 1967.
Потапов, М. К., Олехник, С. Н., Нестеренко, Ю. В. Конкурсные задачи по математике: справочное пособие. - М.: Наука, 1992.-480 с.

Решение задач и выполнение заданий с комментариями, ответами для подготовки к единому государственному экзамену: в 2 ч. - Ч. II / сост. В. Н. Студенецкая, 3. С. Гребнева - Волгоград: Учитель, 2003. - 104 с.
Свечников, А. А. Путешествие в историю математики, или
Как люди учились считать: книга для тех, кто учит и учится. - М.:
Педагогика-Пресс, 1995. - 168 с.
Соболь, Б. В., Виноградова, И. Ю., Рашидова, Е. В. Пособие
для подготовки к единому государственному экзамену и централизованному тестированию по математике. - 3-е изд.- Ростов-на-Дону: Феникс, 2003. - 352 с..
Шевкин, А. В. Текстовые задачи. - М.: Просвещение, 1997.
Фридман Л.М. и др. Как научиться решать задачи: Беседы о решении математических задач. – М., Просвещение 1979.
Дорофеева А.В. Страницы истории на уроках математики. – Львов, журнал «Квантор» 1991.
Пичурин Л.Ф. За страницами учебника алгебры. – М. Просвещение, 1990.
Крамор В.С. Повторяем и систематизируем школьный курс алгебры. – М.: Просвещение, 1990.
Симонов А.Я. и др. Система тренировочных задач и упражнений по математике. – М.: Просвещение, 1991.

1 2 3 4