элективный курс Математика вокруг нас. эл курс матем.вокруг нас.... Симметрия вокруг нас
 Скачать 0.99 Mb.
|
|
Структура программы 1 Пояснительная записка. 2 Цели курса. 3 Содержание курса. 4 Тематическое планирование. 5 Требования к умениям и навыкам. Пояснительная записка. и снительная записка Тема «Симметрия вокруг нас» создана как для реализации в классах гуманитарного профиля, так и для учащихся 9 классов, ориентированных на углубленное изучение математики. Для классов гуманитарного профиля, учащиеся которых ориентированны на углубленное изучение истории, литературы, искусства и других областей гуманитарного знания и при этом имеют низкий уровень интереса и мотивации к изучению математики. Содержание имеет определённое отличие от базового курса математики. В базовом курсе представлена лишь математическая составляющая свойств симметрии, а об их общекультурном аспекте упоминается вскользь. Тема «Симметрия вокруг нас» направлена на интеграцию знаний, формирование общекультурной компетентности, создание представлений о математике как о науке, возникшей из потребностей человеческой практики. Данная тема представляет следующие цели: Показать связь между разными областями знаний; Расширить кругозор учащихся; Стимулировать познавательные интересы. Основные задачи данного курса: Расширить представления учащихся о сферах применения математики; Расширить сферу математических знаний (пространственные фигуры, виды симметрии); Расширить общекультурный кругозор учащихся посредством знакомства их с образцами произведений искусства; Убедить в практической необходимости владения способами выполнения математических действий; Помочь осознать степень интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы (профессии художника, архитектора, инженера), Результатами могут быть следующие умения: Использовать математические знания, алгебраический и геометрический материал для описания и решения задач в будущей профессии; Применять приобретённые геометрические представления, алгебраические преобразования для описания и анализа закономерностей, существующих в окружающем мире; Владея геометрическим языком и изобразительными навыками, понимать и уметь изображать рисунки и схемы; Проводить обобщения и открывать закономерности на основе анализа частных приёмов, экспериментов, выдвигать гипотезы и делать проверки; Уметь соотносить свою точку зрения с мнением авторитетных источников, находить информацию в разнообразных источниках, обобщать и систематизировать её; Уметь ясно и точно выражать свои мысли в устной и письменной речи. Основные формы организации учебных занятий: лекция, объяснение, беседа, практическая работа, семинар. СОДЕРЖАНИЕ . Тема 1. Симметрия 3 часа) Занятие 1. Симметрия (ПОНЯТИЕ). Виды симметрии: осевая, центральная, поворот, параллельный перенос, зеркальная симметрия. Композиция симметрий. Занятие 2. Симметрия фигур. Распределение по классам. Занятие 3. Практическая работа Тема 2. Симметрия в природе.(2часа) Занятие 4. Симметрия в природе. Симметрия в мире растений, насекомых, рыб, птиц, животных. Симметрия в неживой природе. Асимметрия. Занятие 5. Семинар. Прослушивание рефератов. Тема 3 Симметрия в физике.(2часа). Занятие 7. Симметрия в физике. Симметрия законов природы. Проверка рефератов, творческих заданий. Занятие 1 Семинар. Прослушивание рефератов Тема 4. Симметрия в искусстве ( 4часов) Занятие 8. Симметрия в архитектуре, живописи, литературе, музыке. Занятие 9. Проверка рефератов, творческих заданий. Занятие 10. Симметрия в предметах прикладного искусства. Орнамент. Бордюры. Розетки. Герих. Занятие 11. Практическая работа Тема 5. Симметрия в алгебре. (2 часа) Занятие 12.. Симметрические многочлены от двух переменных. Симметрические системы уравнений. Симметрия в графиках функций. Занятие 13. Практическая работа Темы докладов и сообщений. Симметрия правильных многогранников. Порядок в мире атомов. Загадка бензольного кольца. Полиморфизм. Винты в природе. Молекула ДНК. Законы сохранения энергии и импульса в задачах с биллиардными шарами. Симметрия и законы сохранения. Мир элементарных частиц. Филлотаксис.(листорасположение) Симметрия в архитектуре и строительстве. Симметрия бордюров. Симметрия в химии. Поворотная система розеток. Решётки и зоны Бриллюэна. Симметрия и асимметрия в искусстве. Паркеты из правильных многоугольников. Художественные особенности национальных орнаментов. Художественное своеобразие среднеазиатского архитектурного орнамента. Орнаментальное и геометрическое искусство М.Эшера.(голландский художник) Разработка темы «Проценты» обусловлена непродолжительным изучением темы на первом этапе основной школы, когда учащиеся в силу возрастных особенностей еще не могут получит полноценные представления о процентах, об их роли в повседневной жизни. На последующих этапах обучения повторного обращения к этой теме не предусматривается. Во многих школьных учебниках можно встретить задачи на проценты, однако в них отсутствует компактное и четкое изложение соответствующей теории вопроса. Текстовые задачи включены в материалы итоговой аттестации за курс основной школы, в КИМы, и ЕГЭ, в конкурсные экзамены. Однако практика показывает, что задачи на проценты вызывают затруднения у учащихся и очень многие окончившие школу не имеют прочных навыков обращения с процентами в повседневной жизни. Понимание процентов и умение производить процентные расчеты в настоящее время необходимы каждому человеку: прикладное значение этой темы очень велико и затрагивает финансовую, демографическую, социологическую и другие стороны нашей жизни. Тема «Процентные расчеты на каждый день» демонстрирует учащимся применение математического аппарата к решению повседневных бытовых проблем каждого человека, вопросов рыночной экономики и задач технологии производства; ориентирует учащихся на обучение по естественно-научному и социально-экономическому профилю. Познавательный материал курса будет способствовать не только выработке умений и закреплению навыков процентных вычислений, но и формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также познавательной и социальной активности. Данная тема предполагает компактное и четкое изложение теории вопроса, решение типовых задач, самостоятельную работу. Логический анализ содержания темы «Проценты» позволил выделить группы задач, которые и составили основу изучаемого курса. Каждой группе задач предшествует небольшая историческая и теоретическая справка. Кроме того, рассматриваются задачи с практическим содержанием, а именно такие задачи, которые связаны с применением процентных вычислений в повседневной жизни. Предлагаемые задачи различны по уровню сложности: от простых на применение изученных формул до достаточно трудных примеров расчета процентов. Каждое занятие состоит из двух частей: задачи, решаемые с учителем, и задачи для самостоятельного (или домашнего) решения. Основные формы организации учебных занятий: рассказ, беседа, семинар. Разнообразный дидактический материал дает возможность отбирать дополнительные задания для учащихся разной степени подготовки: уровень сложности задач варьируется от простых до конкурсных и олимпиадных. Содержание материала курса показывает связь математики с другими областями знаний, иллюстрирует применение математики в повседневной жизни, знакомит учащихся с некоторыми историческими сведениями по данной теме. Все занятия направлены на развитие интереса школьников к предмету, на расширение представление об изучаемом материале, на решение новых и интересных задач. Цели : Сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач, показав широту применения процентных расчетов в реальной жизни; Способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем. Задачи : Сформировать умения производить процентные вычисления, необходимые для применения в практической деятельности; Решать основные задачи на проценты, применять формулу сложных процентов; Привить учащимся основы экономической грамотности; Помочь ученику оценить свой потенциал с точки зрения образовательной перспективы. Требования к умениям и навыкам В результате изучения темы учащиеся должны: Понимать содержательный смысл термина «процент» как специального способа выражения доли величины; Уметь соотносить процент с соответствующей дробью (особенно в некоторых специальных случаях: 50% - ½; 20% - 1/5; 25% - ¼; и т.д.); Знать широту применения процентных вычислений в жизни, решать основные задачи на проценты, применять формулу сложных процентов; Производить прикидку и оценку результатов вычислений; При вычислениях сочетать устные и письменные приемы, применять калькулятор, использовать приемы, рационализирующие вычисления. В силу большой практической значимости данная тема вызывает интерес, является средством обучения и средством развития интеллектуальных качеств личности учащихся. Для учащихся, которые пока не проявляют заметной склонности к математике, эти занятия могут стать толчком в развитии интереса к предмету и вызвать желание узнать больше. Содержание . Тема 1. Проценты в торговле (3 часа). Введение базовых понятий экономики: процент прибыли, стоимость товара, заработная плата, бюджетный дефицит и профицит, изменение тарифов, пеня и др. Сообщается история появления процентов, устраняются пробелы в знаниях по решению основных задач на проценты: а) нахождение процента от числа (величины); б) нахождение числа по его проценту; в) нахождение процента одного числа от другого. Актуализируются знания об арифметических и алгебраических приемах решения задач на проценты в области торговли. Метод обучения: лекция, практикум по решению задач. Форма контроля: проверка самостоятельно решенных задач, самостоятельная работа. Тема 2. Процентные расчеты в жизненных ситуациях.(3 часа). Показ широты применения в жизни процентных расчетов. Тема знакомит с математикой как с общекультурной ценностью, выработка понимания ими того, что математика является инструментом познания окружающего мира и самого себя. Выполнение тренировочных упражнений. Форма занятий: объяснение, практическая работа. Метод обучения: выполнение тренировочных задач. Формы контроля: проверка самостоятельно решенных задач. Тема 3. Задачи на смеси, концентрацию. (2 час). Усвоение учащимися понятий концентрации вещества, процентного раствора. Формирование умения работать с законом сохранения массы. Обобщение полученных знаний при решении задач на проценты. Форма занятий: комбинированные занятия. Метод обучения: рассказ, объяснение, выполнение практических заданий. Тема 4:Решение задач из области статистики (3часа) Тема способствует осознанию учащимися необходимости знания различных статистических данных: роста или падения цен, производства, численности населения страны, города или какого-нибудь населенного пункта, социальный статус населения. Форма занятий: комбинированные занятия. Метод обучения: рассказ, объяснение, выполнение практических заданий. Тема 5:Решение задач из области спорта (1час) Тема способствует расширению жизненного кругозора учащихся в области спорта. Ведущий подход, используемый при разработке темы, можно выразить в таком лозунге – «С математикой – к ученику посредством раскрытия её с неожиданной стороны». Форма занятий: комбинированные занятия. Метод обучения: рассказ, объяснение, выполнение практических заданий. Тема 6: Банковские операции (3часа) Показ широты применения в жизни процентных расчетов. Введение базовых понятий экономики: процент прибыли, стоимость товара, заработная плата, бюджетный дефицит и профицит, изменение тарифов, пеня и др. Решение задач, связанных с банковскими расчетами: вычисление ставок процентов в банках; процентный прирост; определение начальных вкладов. Форма занятий: объяснение, практическая работа. Метод обучения: выполнение тренировочных задач. Формы контроля: проверка самостоятельно решенных задач Обобщающий урок: решение задач по всему разделу курса Заключительное занятие.(1 час). Итоговая проверочная работа. (1 час). Тема «Методы решения задач на преобразование выражений» является курсом по выбору для учащихся 9 класса. Курс рассчитан на 12 часов, которые проводятся по одному часу в неделю. В этом курсе будут рассмотрены основные методы решения задач на преобразование выражений. При изложении методов решения задач объединены в один вид такие задачи, которые в школе изучаются в разных классах. Цели : Выявление интересов ребенка; Развитие творческого потенциала учащихся; Развитие кругозора школьников. Содержание. 1. Виды выражений и сущность их преобразований Под выражением понимается запись, составленная из чисел и переменных (букв), соединенных знаками действий или функций и скобками. В зависимости от того, входят или не входят в выражения буквенные переменные, выражения делятся на числовые и на выражения с переменными (буквенные выражения). Примеры числовых выражений: 2,4—(5,6+ 3,78): 4,2;  ; sin36° + cos 18° и т. д. Всякое числовое выражение есть число, поэтому его преобразование состоит в записи этого числа другим способом, в другой форме, т. е. в нахождении числа, равного данному, но записанного иначе. Например, выражение 23 + 4 5 можно преобразовать в выражение 22 7, или 28. Таким образом, всякое число можно рассматривать как числовое выражение.Преобразование некоторых числовых выражений сводится к выполнению тех действий, знаками которых соединены числа, входящие в выражение. Например, если в выражении 282 — (72:4 + 60:5) 7 произвести в определенном порядке все указанные действия, то найдем, что оно равно выражению (числу) 72.В других случаях для преобразования числовых выражений приходится использовать довольно сложные приемы. | Всякое выражение с переменными можно рассматривать как функцию этих переменных, принимающую разные числовые значения при разных значениях этих переменных. Так, например, выражение  есть функция от трех переменных а, в и с. Если этим переменным дать какие-то числовые значения из области их изменения, то и само выражение примет соответствующее значение. Если, например, а=1, в=2, с=-1, то это выражение равно 7, если а=2, в=- 1, с = 3, то выражение равно —22 и т. д.Выражения с переменными делятся на виды в зависимости от того, какими действиями или функциями связаны эти переменные. Различают следующие виды выражений с переменными: Одночлены — переменные связаны действиями умноже- ния и возведение в натуральную степень. Многочлены — сумма одночленов. Целые рациональные выражения — переменные связаны действиями сложения, вычитания, умножения и возведение в натуральную степень. 4.Дробные выражения — частное двух целых рациональных выражений. 5.Рациональные выражения — переменные связаны действиями сложения, вычитания, умножения, деления и возведение в любую целую степень. 6. Иррациональные выражения — переменные, кроме указанных выше действий, связаны еще действиями извлечения корня или возведение в дробную степень. 7. Показательные выражения — переменные находятся в показателе степени. Тригонометрические выражения — переменные находятся под знаком тригонометрических функций. Областью определения выражения с переменными называется множество систем значений этих переменных, при которых это выражение имеет смысл, т. е. может быть вычислено. Заметим, что эта область зависит от множества чисел, в котором это выражение рассматривается. Например, область определения выражения  , рассматриваемого на множестве натуральных чисел, такая: у—любое натуральное число (число 0 не рассматривается при этом как натуральное), a x=ky, где k—произвольное натуральное число; область определения того же выражения, рассматриваемого на множестве рациональных или действительных чисел, уже другая: х—любое число, а  .Если выражение  рассматривать на множестве натуральных (или рациональных) чисел, то область его определения такова:  , где k—произвольное натуральное (рациональное) число; если же это выражение рассматривать на множестве действительных чисел, то область его определения есть множество действительных чисел, удовлетворяющих неравенству  .Когда говорят о преобразованиях выражений, то имеют в виду замену данного выражения каким-либо другим на основе определенных правил. В школе рассматриваются главным образом тождественные преобразования выражений с переменными, когда данное выражение заменяется тождественно равным ему выражением, но обладающим каким-либо определенным свойством (оно, например, является выражением стандартного вида или представляет собой произведение многочленов и т. п.). Два выражения называются тождественно равными, если все их соответственные значения равны. При этом соответственными значениями двух выражений с общими переменными называются значения этих выражений, получаемые при одних и тех же значениях этих переменных, взятых из общей области определения этих переменных. Наряду с такой трактовкой тождественных преобразований выражений с переменными, принятой в школьных учебниках математики, можно дать и другую трактовку этих преобразований. Вы знаете, что действия над числами обладают особыми свойствами, называемыми законами действий. К ним относятся переместительный и сочетательный законы сложения, такие же законы умножения, распределительный закон и др. Для других действий имеются другие законы, например (а")т = апп. Кроме того, сами определения этих действий (вычитания, деления, возведение в степень) можно рассматривать как своеобразные законы. На основе этих законов в школьном курсе математики доказаны многие тождества, такие, например: 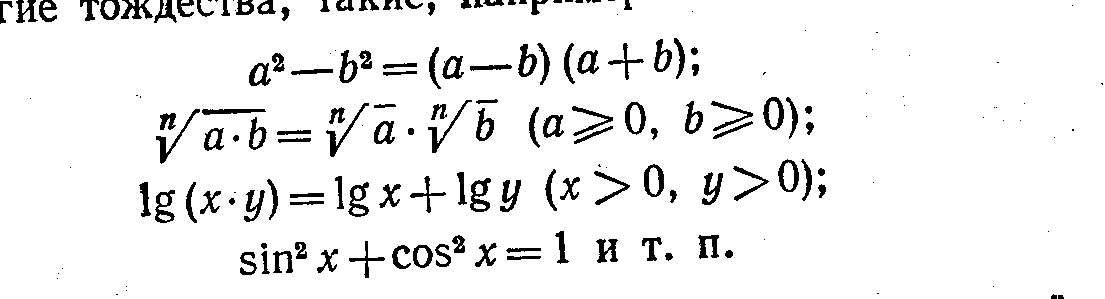 Все эти определения, законы действий, тождества и свойства функций можно рассматривать как общие правила тождественных преобразований выражений с переменными. Любое из них представляет собой тождественное равенство. При этом во всех этих правилах буквы обозначают не только какие-то переменные, но и целые выражения. Поэтому любое такое правило применимо к соответствующим выражениям и в результате его применения мы всегда получаем тождественно равное выражение (конечно, в общей области определений исходного и преобразованного выражений). Например, если мы имеем выражение  , то, применяя к нему распределительный закон, получим:(2а2 + в3) • Зс2 = (2а2) (Зс2) + (в3) (Зс2). К полученному выражению можно применить переместительный и сочетательный законы умножения:  Итак, мы видим, что тождественные преобразования выражений с переменными можно понимать как последовательное применение к данному выражению общих правил таких преобразований. Тогда под тождественно равными выражениями будем понимать такие выражения, которые получаются одно из другого в результате последовательного применения общих правил тождественных преобразований. Например, если к выражению 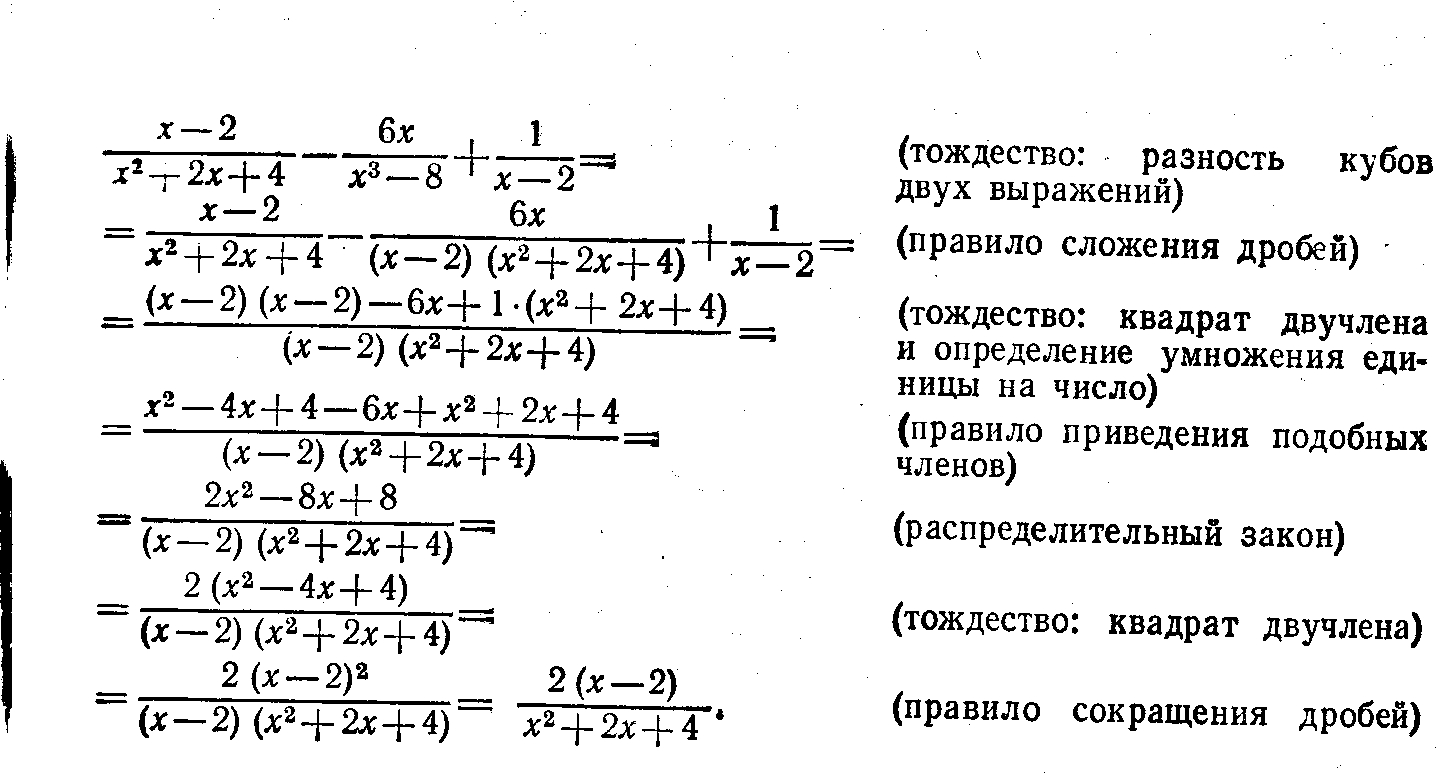 последовательно применять указанные ниже справа в скобках общие правила тождественных преобразований, то будем получать выражения, тождественно равные данному выражению (конечно, лишь при условии  .  устраняются пробелы в (тождество: разность кубов двух выражений) (правило сложения дробей) (тождество: квадрат двучлена и определение умножения единицы) (правило приведения подобных членов) (распределительный закон) (тождество: квадрат двучлена) Теперь вам должно быть ясно, что, для того чтобы произвести какое-либо тождественное преобразование заданного выражения, нужно умело выбрать ннеобходимую последовательность общих правил этих преобразований и применить их одно за ддругим к данному выражению, пока не получим требуемую форму выражения. Поэтому понятно, чдля чето нужно хорошо знать все эти общие правила преобразований. Приведем перечень основных общих правил тождественных преобразований. Для облегчения запоминания разобьем их на группы. I группа. Законы сложения и умножения a+b=b+a(переместительный закон сложения). (a+b)+c=a+(b+c) (сочетательный закон сложения). ab=ba(переместительный закон умножения). (ab)c = a(bc) (сочетательный закон умножения). (a+b)c = ac+bc(распределительный закон). Если а=Ь и с—любое число, то a+c=b+c. Если а = Ь и с  0, то ас=Ьс.II группа. Определения и свойства вычитания и деления. Если a-Ь=с, то a=b+c (определение разности). a – b= a+(-b) (замена вычитания сложением). a + (b – c) = a + b – c  (правило раскрытия скобок)a – (b – c )= a – b + c (правило раскрытия скобок) 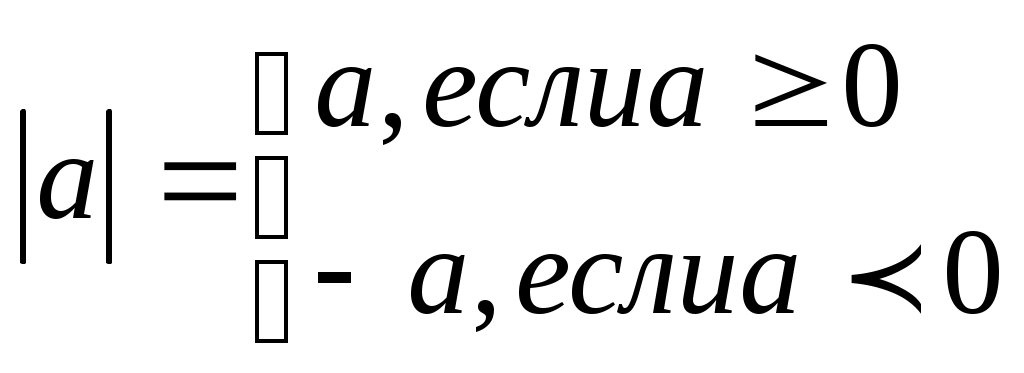 (определение модуля числа).Если а:Ь=с, то а=Ьс (определение частного). III группа. Особые случаи действий 111.I. a+0=0+a=a (прибавление нуля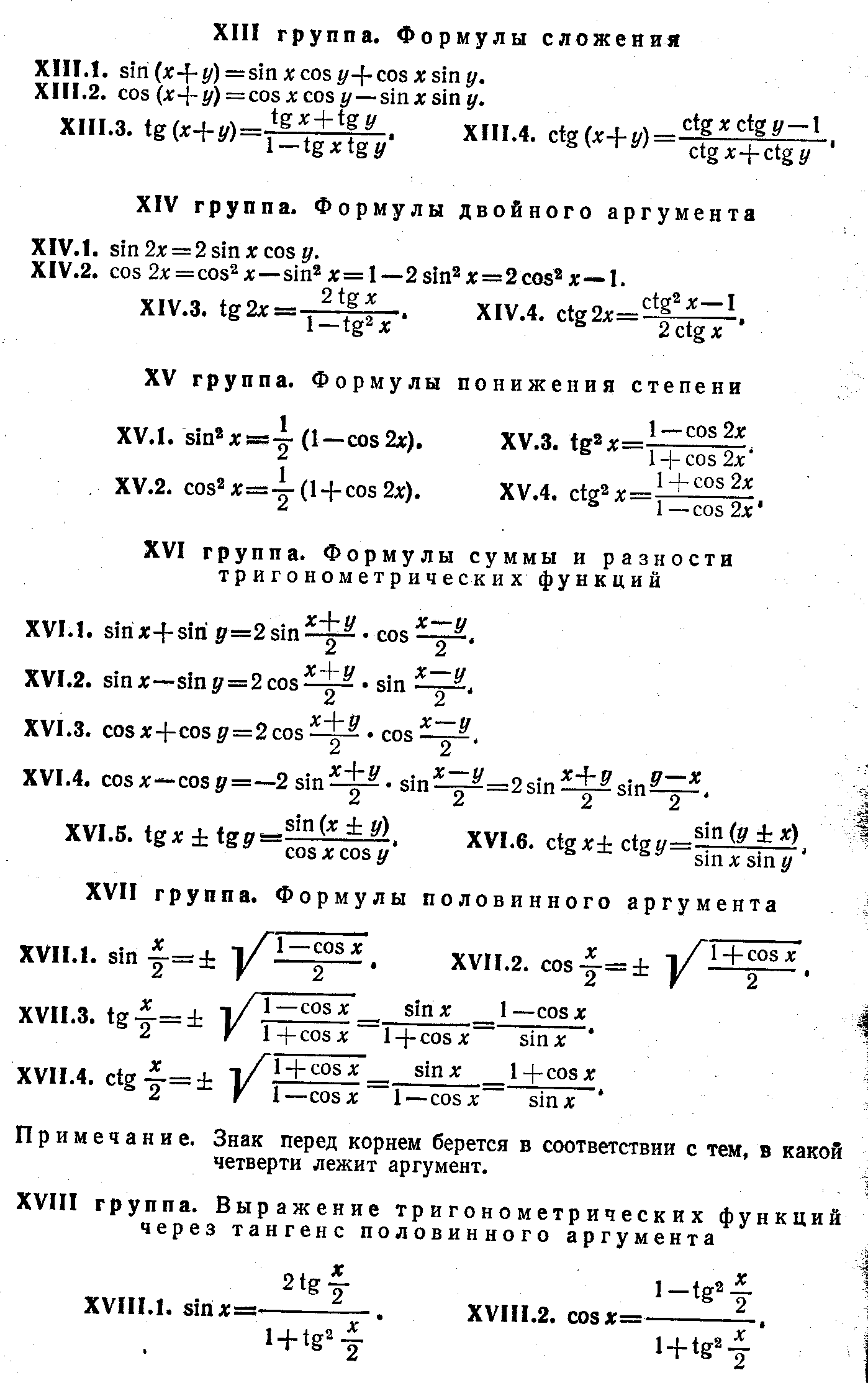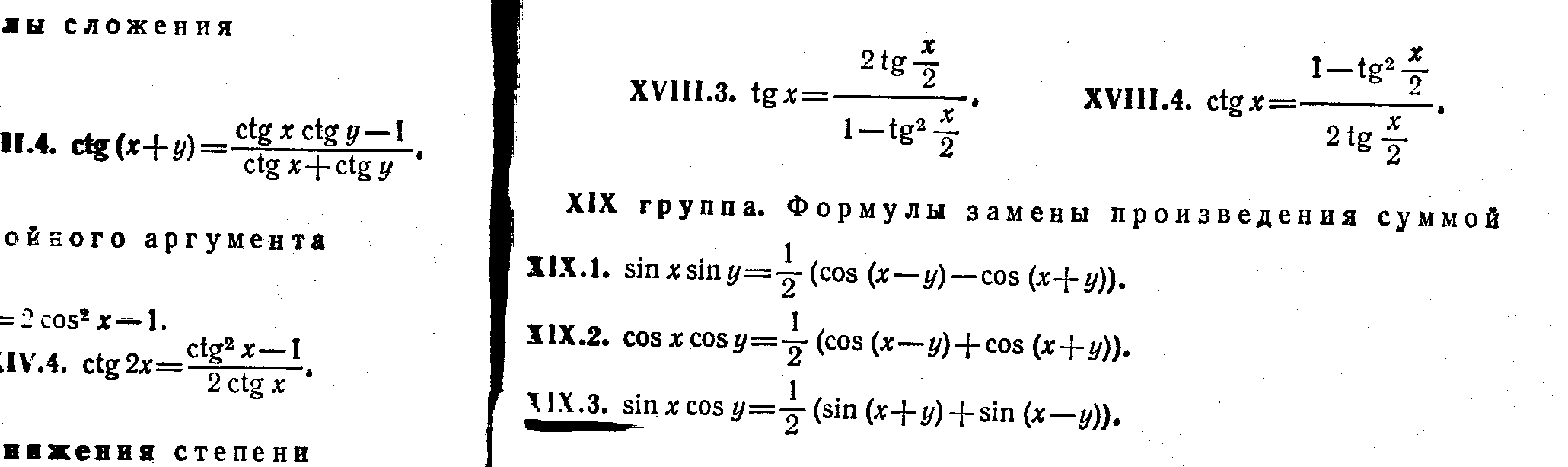).  (умножение на единицу). (умножение на нуль)Ш.4. 0:а = 0 (а 0) (деление нуля).     Обращаем еще раз ваше внимание на то, что во всех этих формулах буквы обозначают не только отдельные переменные, но и любые выражения с переменными. Также важно заметить, что любую из этих формул преобразований можно рассматривать (читать) как слева направо, так и справа налево. Например, если правило 1.5 читать слева направо, то оно выражает распределительный закон, позволяющий раскрывать скобки в произведении; если же это правило читать права налево, то оно выражает правило вынесения общего множителя за скобки. Формула VI.4 слева направо выражает правило разложения суммы кубов на множители; читая же ее справа налево, она выражает правило умножения суммы двух выражений на неполный квадрат разности этих выражений и т. д. Особо следует сказать о формулах, выражающих свойства тригонометрических функций (X — XIX). В этих формулах не указывали области, в которых они справедливы. Но следует иметь в виду известные ограничения на области определения тригонометрических функций. Заметьте также, что приведенные формулы не независимы друг от друга. Некоторые из них являются следствиями других. Например, формулы понижения степени тригонометрических функций (XV группа) являются следствиями формул половинного аргумента и т. д. Но для удобства пользования этими правилами и формулами привели их все. УЧЕБНО - ТЕМАТИЧЕСКИЙ ПЛАН.
|