Simulink Инструмент моделирования динамических систем
 Скачать 2.28 Mb. Скачать 2.28 Mb.
|
|
A –Матрица системы. B – Матрица входа. C – Матрица выхода D – Матрица обхода Initial condition – Вектор начальных условий. Absolute tolerance — Абсолютная погрешность. На рис. 9.3.11 показан пример моделирования динамического объекта с помощью блока State-Space. Матрицы блока имеют следующие значения: 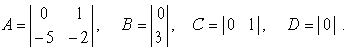 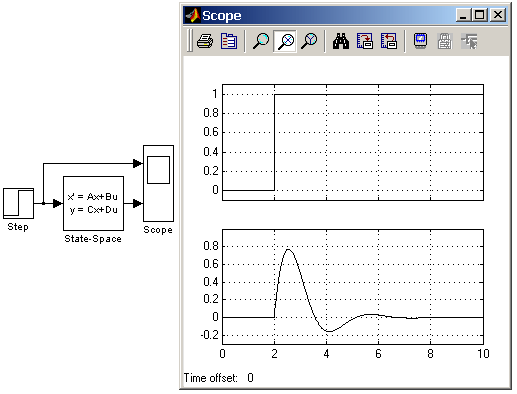 Рис. 9.3.12. Пример использования блока State-Space. 9.4. Discrete – дискретные блоки 9.4.1. Блок единичной дискретной задержки Unit Delay Назначение: Выполняет задержку входного сигнала на один шаг модельного времени. Параметры:
Входной сигнал блока может быть как скалярным, так и векторным. При векторном входном сигнале задержка выполняется для каждого элемента вектора. Блок поддерживает работу с комплексными и действительными сигналами. На рис. 9.4.1 показан пример использования блока для задержки дискретного сигнала на один временной шаг, равный 0.1с. 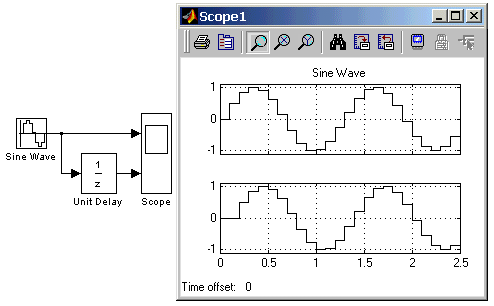 Рис. 9.4.1. Пример использования блока Unit Delay 9.4.2. Блок экстраполятора нулевого порядка Zero-Order Hold Назначение: Блок выполняет дискретизацию входного сигнала по времени. Параметры: Sample time – Величина шага дискретизации по времени. Блок фиксирует значение входного сигнала в начале интервала квантования и поддерживает на выходе это значение до окончания интервала квантования. Затем выходной сигнал изменяется скачком до величины входного сигнала на следующем шаге квантования. На рис. 9.4.2 показан пример использования блока Zero-Order Hold для формирования дискретного сигнала. 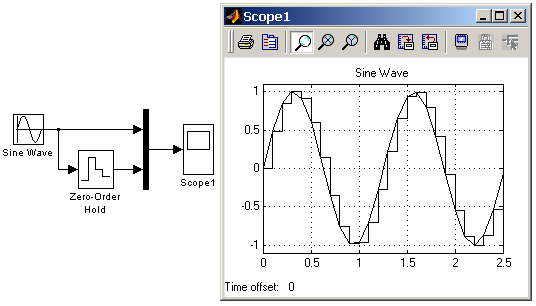 Рис. 9.4.2. Пример формирования дискретного сигнала с помощью блока Zero-Order Hold Блок экстраполятора нулевого порядка может использоваться также для согласования работы дискретных блоков имеющих разные интервалы квантования. На рис. 9.4.3 показан пример такого использования блока Zero-Order Hold. В примере блок Discrete Transfer Fcn имеет параметр Sample time = 0.4 , а для блока Discrete Filter этот же параметр установлен равным 0.8. 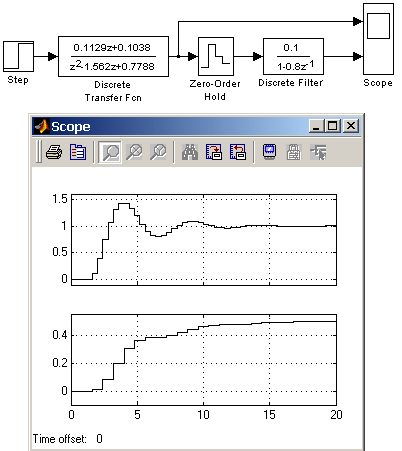 Рис. 9.4.3. Использование блока Zero-Order Hold для согласования работы дискретных блоков. 9.4.3. Блок экстраполятора первого порядка First-Order Hold Назначение: Блок задает линейное изменение выходного сигнала на каждом такте дискретизации, в соответствии с крутизной входного сигнала на предыдущем интервале дискретизации. Параметры: Sample time – Величина шага дискретизации по времени. Пример экстраполяции синусоидального сигнала этим блоком показан на рис. 9.4.4. 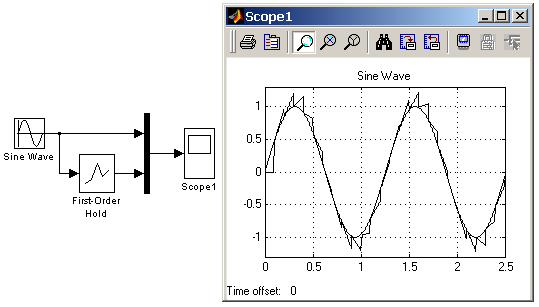 Рис. 9.4.4. Использование блока First-Order Hold 9.4.4. Блок дискретного интегратора Discrete-Time Integrator Назначение: Блок используется для выполнения операции интегрирования в дискретных системах. Параметры:
Метод использует аппроксимацию T/(z-1) передаточной функции 1/s. Выходной сигнал блока рассчитывается по выражению: y(k) = y(k–1) + T*u(k–1), y – выходной сигнал интегратора, u – входной сигнал интегратора, T – шаг дискретизации, k – номер шага моделирования.
Метод использует аппроксимацию T*z/(z–1) передаточной функции 1/s. Выходной сигнал блока рассчитывается по выражению: y(k) = y(k–1) + T*u(k).
Метод использует аппроксимацию T/2*(z+1)/(z–1) передаточной функции 1/s. Выходной сигнал блока рассчитывается по выражению: x(k) = y(k–1) + T/2 * u(k–1).
Остальные параметры дискретного интегратора те же, что и у блока аналогового интегратора Integrator (библиотека Continuous). На рис. 9.4.5 показан пример демонстрирующий все три способа численного интегрирования блока Discrete-Time Integrator. Как видно из рисунка изображение блока меняется в зависимости от выбранного метода интегрирования. 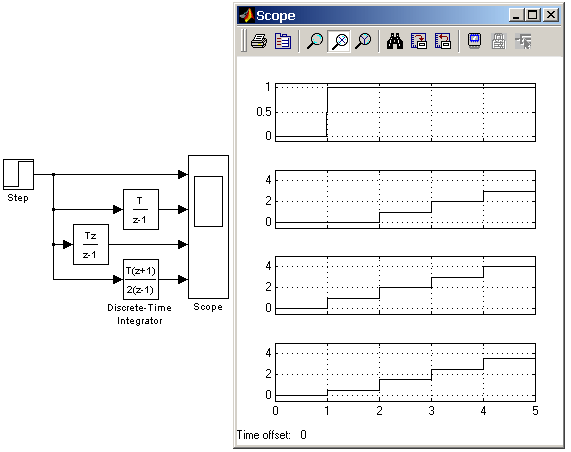 Рис. 9.4.5. Выполнение интегрирования блоками Discrete-Time Integrator, реализующими разные численные методы. 9.4.5. Дискретная передаточная функция Discrete Transfer Fсn Назначение: Блок Discrete Transfer Fcn задает дискретную передаточную функцию в виде отношения полиномов: 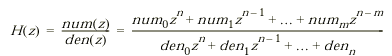 , ,где m+1и n+1 – количество коэффициентов числителя и знаменателя, соответственно. num – вектор или матрица коэффициентов числителя, den – вектор коэффициентов знаменателя. Параметры:
Порядок числителя не должен превышать порядок знаменателя. Входной сигнал блока должен быть скалярным. В том случае, если коэффициенты числителя заданы вектором, то выходной сигнал блока будет скалярным (также как и входной сигнал). На рис. 9.4.6 показан пример использования блока Discrete Transfer Fcn. В примере рассчитывается реакция на единичное ступенчатое воздействие дискретного аналога колебательного звена: Шаг дискретизации выбран равным 0.5 с. 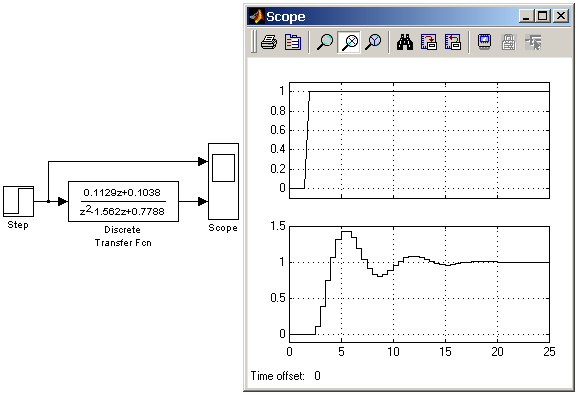 Рис. 9.4.6. Использование блока Discrete Transfer Fcn 9.4.6. Блок дискретной передаточной функции Discrete Zero-Pole Назначение: Блок Discrete Zero-Pole определяет дискретную передаточную функцию с заданными полюсами и нулями: где Z – вектор или матрица нулей передаточной функции, P – вектор полюсов передаточной функции, K – коэффициент передаточной функции, или вектор коэффициентов, если нули передаточной функции заданы матрицей. При этом размерность вектора K определяется числом строк матрицы нулей. Параметры:
Количество нулей не должно превышать число полюсов передаточной функции. В том случае, если нули передаточной функции заданы матрицей, то блок Discrete Zero-Pole моделирует векторную передаточную функцию. Нули или полюса могут быть заданы комплексными числами. В этом случае нули или полюса должны быть заданы комплексно-сопряженными парами полюсов или нулей, соответственно. Начальные условия при использовании блока Discrete Zero-Pole полагаются нулевыми. На рис. 9.4.7 показан пример использования блока Discrete Zero-Pole. С помощью рассматриваемого блока моделируется дискретный аналог передаточной функции Шаг дискретизации выбран равным 0.5 с. 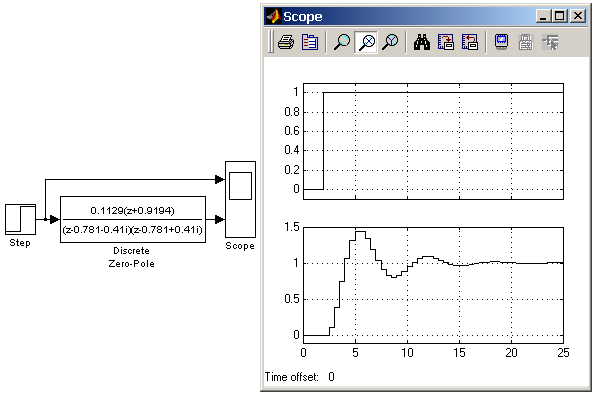 Рис. 9.4.7. Использование блока Discrete Zero-Pole. 9.4.7. Блок дискретного фильтра Discrete Filter Назначение: Блок дискретного фильтра Discrete Filter задает дискретную передаточную функцию от обратного аргумента (1/z): m+1и n+1 – количество коэффициентов числителя и знаменателя, соответственно. num – вектор или матрица коэффициентов числителя, den – вектор коэффициентов знаменателя. Параметры:
На рис. 9.4.8 показан пример использования блока Discrete Filter. С помощью рассматриваемого блока моделируется дискретный аналог передаточной функции: Шаг дискретизации выбран равным 0.5 с. 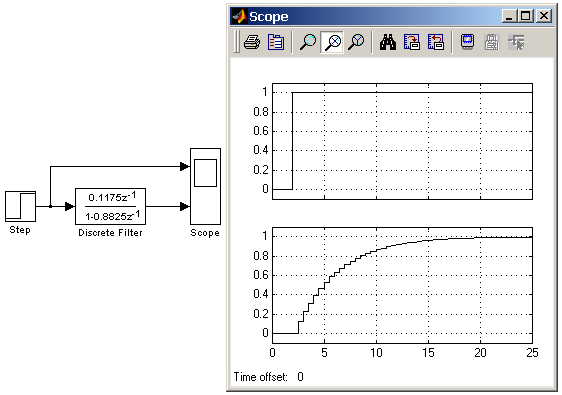 Рис. 9.4.8. Использование блока Discrete Filter. 9.4.8. Блок модели динамического объекта Discrete State-Space Назначение: Блок создает динамический объект, описываемый уравнениями в пространстве состояний: где x – вектор состояния, u – вектор входных воздействий, y – вектор выходных сигналов, A, B, C, D - матрицы: системы, входа, выхода и обхода, соответственно, n – номер шага моделирования. Размерность матриц показана на рис. 9.4.9 (n – количество переменных состояния, m – число входных сигналов, r – число выходных сигналов). 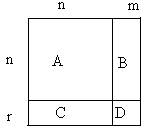 Рис. 9.4.9. Размерность матриц блока Discrete State-Space Параметры:
На рис. 9.4.10 показан пример моделирования динамического объекта с помощью блока Discrete State-Space. Матрицы блока имеют следующие значения: 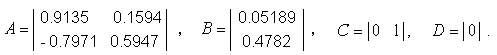 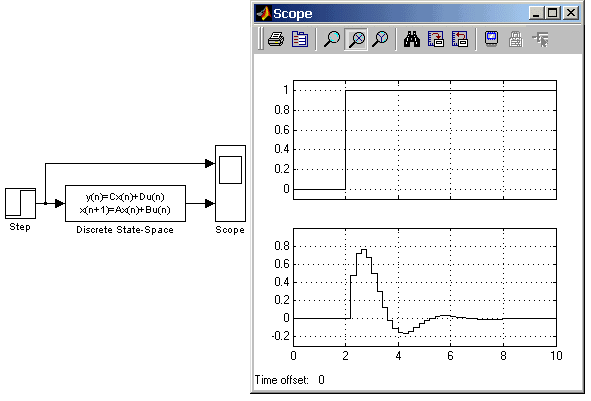 Рис. 9.4.10. Пример использования блока Discrete State-Space. 9.5. Nonlinear - нелинейные блоки 9.5.1. Блок ограничения Saturation Назначение: Выполняет ограничение величины сигнала. Параметры:
Выходной сигнал блока равен входному если его величина не выходит за порог ограничения. По достижении входным сигналом уровня ограничения выходной сигнал блока перестает изменяться и остается равным порогу. На рис. 9.5.1 показан пример использования блока для ограничения синусоидального сигнала. На рисунке приводятся временные диаграммы сигналов и зависимость выходного сигнала блока от входного. 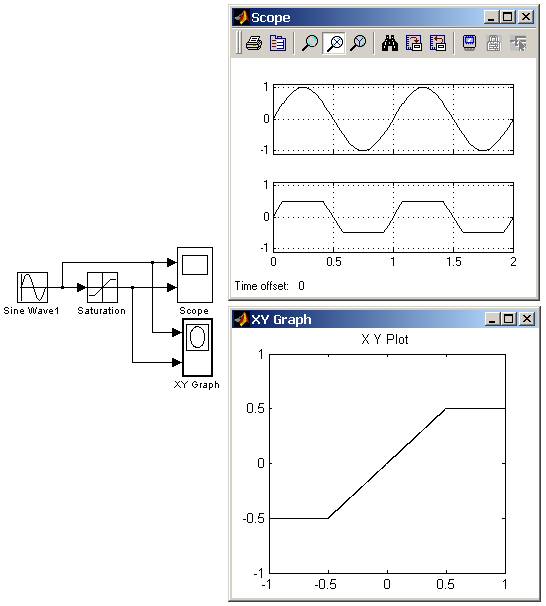 Рис. 9.5.1. Пример использования блока Saturation 9.5.2. Блок с зоной нечувствительности Dead Zone Назначение: Реализует нелинейную зависимость типа "зона нечувствительности (мертвая зона)". Параметры:
Выходной сигнал блока вычисляется в соответствии со следующим алгоритмом:
На рис. 9.5.2 показан пример использования блока Dead Zone 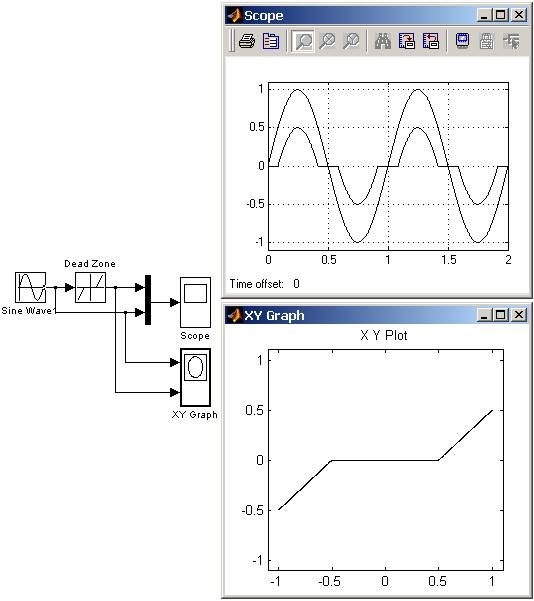 Рис. 9.5.2. Пример использования блока Dead Zone 9.5.3. Релейный блок Relay Назначение: Реализует релейную нелинейность. Параметры:
Выходной сигнал блока может принимать два значения. Одно из них соответствует включенному состоянию реле, второе - выключенному. Переход их одного состояния в другое происходит скачком при достижении входным сигналом порога включения или выключения реле. В том случае если пороги включения и выключения реле имеют разные значения, то блок реализует релейную характеристику с гистерезисом. При этом значение порога включения должно быть больше, чем значение порога выключения. На рис. 9.5.3 показан пример использования блока Relay. На временных диаграммах видно, что включение реле происходит при достижении входным сигналом величины 0.5, а выключение при - 0.5. 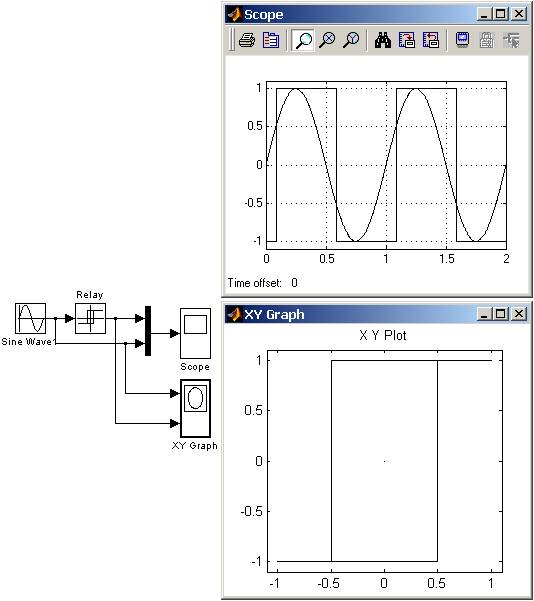 Рис. 9.5.3. Пример использования блока Relay 9.5.4. Блок ограничения скорости изменения сигнала Rate Limiter Назначение: Блок обеспечивает ограничение скорости изменения сигнала (первой производной). Параметры:
Вычисление производной сигнала выполняется по выражению: где u(i) - значение входного сигнала на текущем шаге, t(i) - значение модельного времени на текущем шаге, y(i-1) - значение выходного сигнала на предыдущем шаге, t(i-1) - значение модельного времени на предыдущем шаге. Вычисленное значение производной сравнивается со значениями уровней ограничения скорости Rising slew rate и Falling slew rate. Если значение производной больше, чем значение параметра Rising slew rate, то выходной сигнал блока вычисляется по выражению: где R - уровень ограничения скорости при увеличении сигнала. Если значение производной меньше, чем значение параметра Falling slew rate, то выходной сигнал блока вычисляется по выражению: где F - уровень ограничения скорости при уменьшении сигнала. Если значение производной лежит в пределах между нижним и верхним уровнями ограничения, то выходной сигнал блока равен входному: На рис. 9.5.4 показан пример использования блока Rate Limiter, при подаче на его вход прямоугольного периодического сигнала. 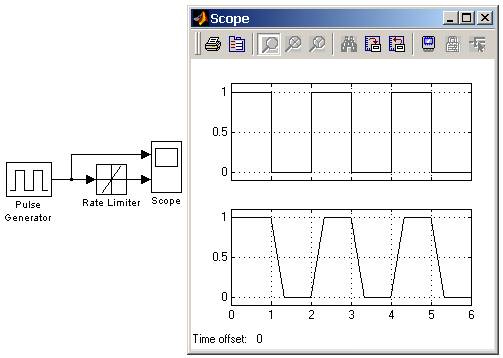 Рис. 9.5.4. Пример использования блока Rate Limiter 9.5.5. Блок квантования по уровню Quantizer Назначение: Блок обеспечивает квантование входного сигнала с одинаковым шагом по уровню. Параметры: |
