Контрольная работа управление тех системами. КР УТС вариант 36. Синтез линейной системы автоматического управления
 Скачать 485.89 Kb. Скачать 485.89 Kb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный индустриальный университет» Кафедра электротехники, электропривода и промышленной электроники РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовой работе по учебной дисциплине «Управление техническими системами» тема: «Синтез линейной системы автоматического управления» Вариант № 36 Выполнил: обучающийся гр._________ _______________________ Проверил: к.т.н., доцент Рыбаков А.И. Новокузнецк 2021 Оглавление1. Анализ исходной САУ. 3 1.1 Определение передаточной функции САУ в разомкнутом состоянии. 3 1.2. Определение требуемого коэффициента усиления разомкнутой САУ из условия статической точности и необходимого диапазона регулирования. 3 1.3. Определение передаточной функции замкнутой САУ по управляющему, возмущающему воздействиям и по ошибке регулирования. 4 2. Анализ устойчивости исходной САУ. 7 2.1. Определение характеристического уравнения системы. 7 2.2. Анализ устойчивости исходной САУ с помощью критерия Гурвица. 7 2.3. Анализ устойчивости исходной САУ с помощью критерия Найквиста. 8 2.4. Анализ исходной САУ по диаграмме Боде. 9 2.5. Определение влияния величины коэффициента усиления САУ на ее устойчивость методом корневого годографа. 10 3. Синтез корректирующих устройств. 12 3.1. Синтез последовательного КУ. 12 3.2. Синтез параллельного КУ. 13 3.3 Структурно-параметрическая синтез оптимизированной САУ. 16 4. Анализ синтезированных САУ. 20 4.1 Анализ синтезированной САУ при последовательной коррекции. 20 4.2 Анализ синтезированной САУ при параллельной коррекции. 22 4.3 Анализ синтезированной САУ при структурно-параметрической оптимизации. 24 4.4 Сравнительный анализ различных способов коррекции. 28 1. Анализ исходной САУ.1.1 Определение передаточной функции САУ в разомкнутом состоянии.Рассмотрим структурную схему исходной САУ: 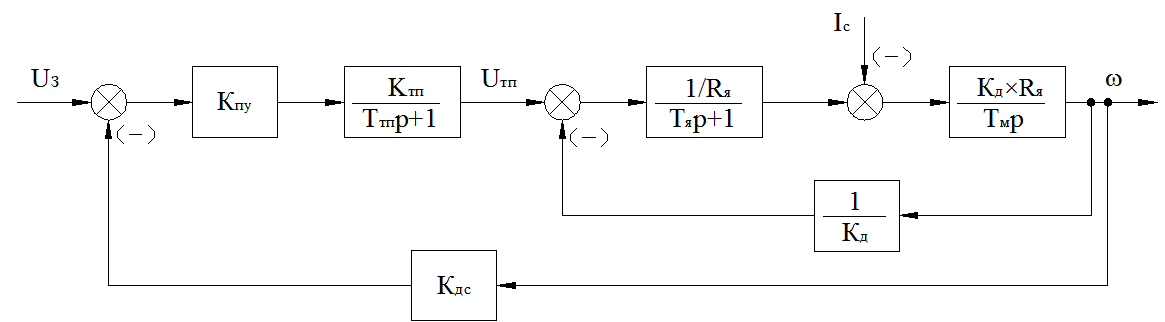   Имеем двухконтурную систему подчиненного регулирования. Найдем передаточную функцию разомкнутой системы, применив правила преобразования структурных схем : 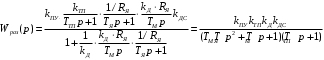 Система может быть представлена состоящей из 3-х звеньев: усилительного, апериодического и звена второго порядка. Так как соблюдается соотношение 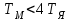 , то звено колебательное. , то звено колебательное.1.2. Определение требуемого коэффициента усиления разомкнутой САУ из условия статической точности и необходимого диапазона регулирования.Требуемый коэффициент усиления с учетом необходимого диапазона регулирования: 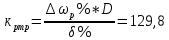 где 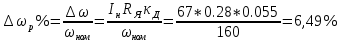 С учетом полученной выше ПФ разомкнутой системы и определения статического режима как режима, в котором приращения координат равны 0, можно записать: 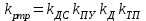 . .Зная  , , 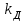 , , 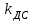 и и 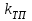 , найдем требуемый коэффициент передачи предварительного усилителя , найдем требуемый коэффициент передачи предварительного усилителя 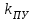 : :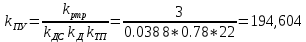 Требуемый 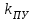 может быть реализован следующей схемой на основе операционного усилителя: может быть реализован следующей схемой на основе операционного усилителя: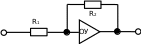 Для подобных схем 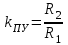 . . Найдем величину статической ошибки при найденном  : :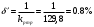 . . Видно, что при данном  статическая ошибка меньше допустимой. Это означает, что исходная система в статическом режиме устойчива. статическая ошибка меньше допустимой. Это означает, что исходная система в статическом режиме устойчива.1.3. Определение передаточной функции замкнутой САУ по управляющему, возмущающему воздействиям и по ошибке регулирования.а) передаточная функция замкнутой системы по управляющему воздействию 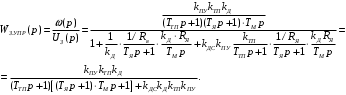 Подставляя численные значения, получаем: 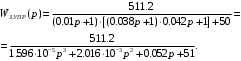 б) передаточная функция замкнутой системы по возмущающему воздействию: 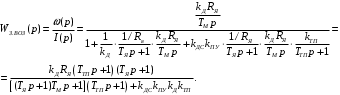 Подставляя численные значения, получаем: 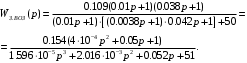 в) передаточная функция замкнутой системы по ошибке. Ошибка: 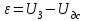 Передаточная функция: 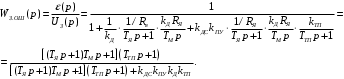 Подставляя численные значения, получаем: 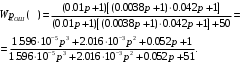 2. Анализ устойчивости исходной САУ.2.1. Определение характеристического уравнения системы.Передаточная функция замкнутой САУ имеет вид: 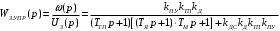 Отсюда получим характеристическое уравнение системы: 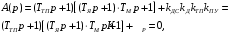 Подставив численные значения, получим: 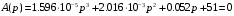 . .В соответствии с общим видом 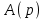 : :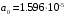 , , 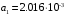 , , 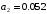 , , 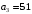 . .2.2. Анализ устойчивости исходной САУ с помощью критерия Гурвица.Для устойчивости линейной САУ необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительными при а0>0. Характеристическое уравнение системы в замкнутом состоянии: 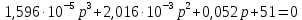 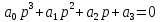 Коэффициенты характеристического уравнения: 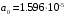 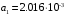 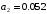 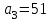 Составляем определитель Гурвица: по главной диагонали записываются коэффициенты характеристического уравнения, начиная с а1, определитель заполняется по столбцам, вниз от главной диагонали записываются коэффициенты с убывающим индексом, вверх – с возрастающим индексом, недостающие коэффициенты заполняются нулями. 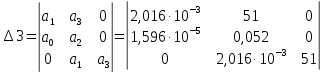 Условие устойчивости: 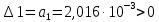 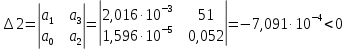 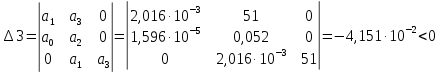 Т.к. определитель Гурвица и его диагональные миноры отрицательные, то делаем вывод, что система неустойчивая. 2.3. Анализ устойчивости исходной САУ с помощью критерия Найквиста.Построим годограф Найквиста для передаточной функции САУ Wраз(р). Для этого заменяем оператор р на комплексную переменную jω 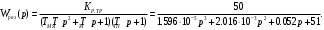 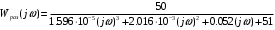 Подставляя значения ω от 0 до +∞ строим на комплексной плоскости годограф Найквиста. 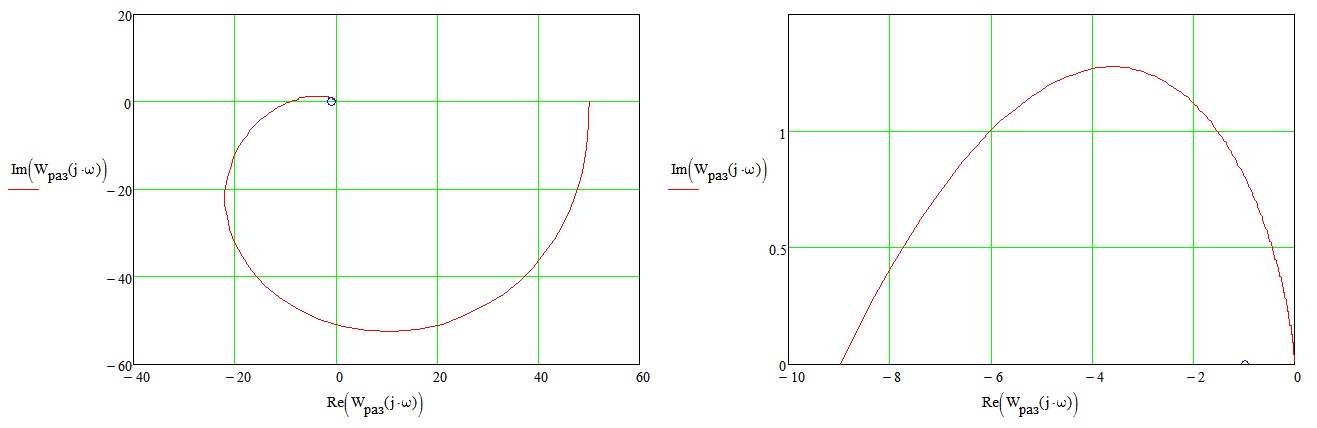 Годограф Найквиста с увеличением частоты охватывает точку с координатами (-1; j0). Значит САУ неустойчива. 2.4. Анализ исходной САУ по диаграмме Боде.Используя программу MatLAB строим диаграмму Боде для исходной САУ. Используем передаточную функцию разомкнутой системы. >>Ta = 0.038; Tm = 0.042; Ttp = 0.01; K = 50; >>Wraz = tf( K, [Ttp 1]) * tf( 1, [Ta*Tm Tm 1]) Transfer function: 50 ------------------------------------------- 1.596e-005 s^3 + 0.002016 s^2 + 0.052 s + 1 >>margin (Wraz) 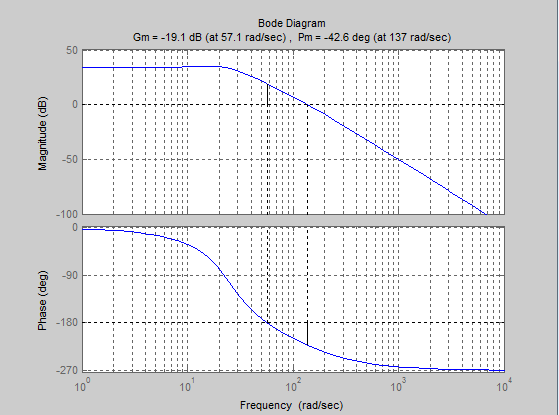 Из диаграммы Боде видно, что система неустойчива. Она обладает отрицательными запасами устойчивости: - по амплитуде: -19.1 дБ; - по фазе: -42.6°. 2.5. Определение влияния величины коэффициента усиления САУ на ее устойчивость методом корневого годографа.С помощью системы MATLAB построим корневой годограф разомкнутой системы. Для этого найдем значения полюсов ПФ: >>Wraz=tf([129.8],[0.00001596 0.002016 0.052 51]) Transferfunction: 129.8 -------------------------------------------- 1.596e-005 s^3 + 0.002016 s^2 + 0.052 s + 51 >>tzero (Wraz) ans = Empty matrix: 0-by-1 >>pole (Wraz) ans = 1.0e+002 * -1.9424 0.3396 + 1.2369i 0.3396 - 1.2369i >>Wzp=zpk ([],[-1.9424 (0.3396 + 1.2369i) (0.3396 - 1.2369i)],129.8) Zero/pole/gain: 129.8 --------------------------------- (s+1.942) (s^2 - 0.6792s + 1.645) >>rlocus (Wzp) 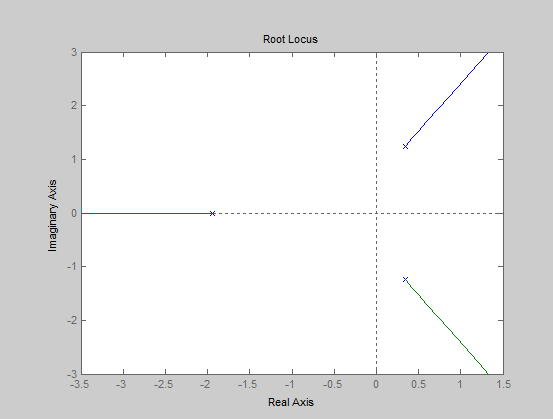 3. Синтез корректирующих устройств.3.1. Синтез последовательного КУ.Для синтеза последовательного КУ построим асимптотическую ЛАХ исходной разомкнутой системы W, желаемую ЛАХ Wж в соответствии с требованиями. Графическим методом найдем ЛАХ корректора: Lк=Lж-Lисх (построение –см. рисунок). По виду ЛАХ корректора по [1,стр.542,табл.П.7] найдем схему последовательного КУ. Данное КУ является пассивным RC-четырехполюсником. 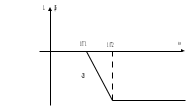 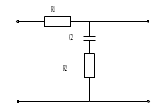   Рис. 3.2Схемная реализация корректирующего устройства Рис. 3.1 ЛАХ корректирующего устройства Передаточная функция корректора: 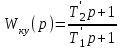 Постоянные времени 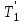 и и 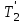 определяются через частоты определяются через частоты 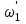 и и 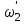 (см. построение ЛАХ корректора) по общей формуле (см. построение ЛАХ корректора) по общей формуле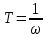 Найдем численные значения постоянных времени: 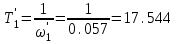 с; с; 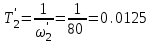 с сИз схемы КУ: 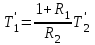 ; ; 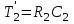 Отсюда: 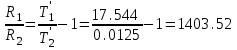 Зная эти соотношения, нетрудно подобрать соответствующие схемные элементы. Выберем по [4] в качестве 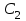 конденсатор К50-6-100мкФ с номинальной емкостью 100 мкФ. Тогда конденсатор К50-6-100мкФ с номинальной емкостью 100 мкФ. Тогда 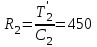 Ом. По справочнику [5, табл.2.2, стр. 20; табл. стр.83] выберем в качестве Ом. По справочнику [5, табл.2.2, стр. 20; табл. стр.83] выберем в качестве 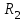 резистор типа МЛТ с номинальным сопротивлением 450 Ом. резистор типа МЛТ с номинальным сопротивлением 450 Ом.Найдем 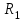 : : 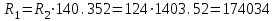 Ом. По тому же справочнику [5, табл.2.2, стр. 20; табл. стр.83] в качестве Ом. По тому же справочнику [5, табл.2.2, стр. 20; табл. стр.83] в качестве 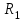 выберем резистор МЛТ с номинальным сопротивлением выберем резистор МЛТ с номинальным сопротивлением 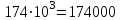 Ом (ряд допусков Е96). Ом (ряд допусков Е96).Постоянные времени КУ с учетом стандартных значений R и C: 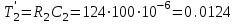 с с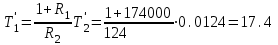 с с3.2. Синтез параллельного КУ.Параллельная коррекция реализуется за счет подключения к какому-либо элементу схемы КУ в качестве обратной связи. Для синтеза параллельного КУ используем желаемую ЛАХ, построенную в предыдущем пункте. Корректирующей ОС целесообразно охватить тиристорный преобразователь и предварительный усилитель. Таким образом, скорректированная схема будет выглядеть следующим образом: 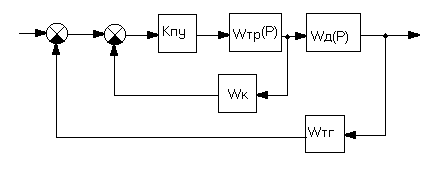 В этой схеме: 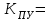 - коэффициент передачи предварительного усилителя; - коэффициент передачи предварительного усилителя;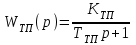 - передаточная функция тиристорного преобразователя; - передаточная функция тиристорного преобразователя;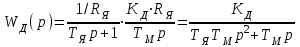 - передаточная функция двигателя; - передаточная функция двигателя;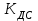 - коэффициент передачи датчика скорости; - коэффициент передачи датчика скорости;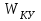 - искомая передаточная функция корректирующего устройства. - искомая передаточная функция корректирующего устройства.Передаточная функция звеньев, охваченных корректирующей ОС: 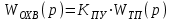 Общая передаточная функция звеньев, охваченных корректирующей ОС, и корректирующего звена: 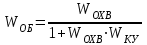 Передаточная функция звеньев, не охваченных корректирующей ОС: 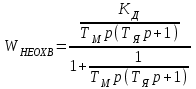 ПФ скорректированной системы при параллельной коррекции: 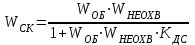 Переходя к ЛАХ: 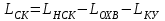 , ,где 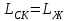 - ЛАХ скорректированной системы (желаемая ЛАХ, см. последовательную коррекцию); - ЛАХ скорректированной системы (желаемая ЛАХ, см. последовательную коррекцию);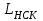 - ЛАХ нескорректированной (исходной) системы; - ЛАХ нескорректированной (исходной) системы;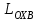 - ЛАХ звеньев, охваченных корректирующей ОС; - ЛАХ звеньев, охваченных корректирующей ОС;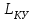 - ЛАХ корректирующего устройства. - ЛАХ корректирующего устройства.Отсюда найдем ЛАХ корректирующего устройства: 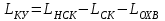 Решение осуществим графически (см. рисунок). Из рисунка видно, что ЛАХ корректирующего устройства имеет следующий вид: 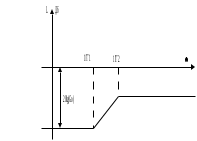 Из [1, стр.542,табл.П.7] по виду ЛАХ найдем схемное решение данного корректирующего устройства: 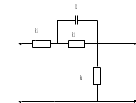 Данное КУ имеет передаточную функцию вида 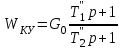 . .Параметры 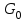 , , 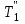 и и 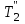 можно определить непосредственно из построения асимптотической ЛАХ корректора. можно определить непосредственно из построения асимптотической ЛАХ корректора.Параметры элементов схемы связаны с параметрами ЛАХ следующими соотношениями: 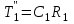 , , 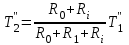 , , 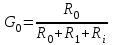 . .Из построения: 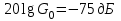 . Отсюда: . Отсюда: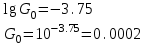 Кроме того, из построения видно, что частоты сопряжения (а, следовательно, и соответствующие им постоянные времени) равны соответствующим для последовательной коррекции, т.е. 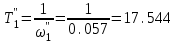 с; с; 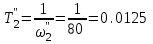 с сЗная 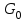 , , 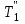 и и 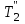 , найдем параметры реальных элементов схемы параллельной коррекции. Для нахождения этих параметров составим систему уравнений: , найдем параметры реальных элементов схемы параллельной коррекции. Для нахождения этих параметров составим систему уравнений: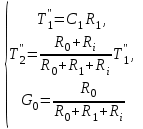 Очевидно, что данная система неразрешима, так как число переменных больше числа уравнений. Поэтому зафиксируем параметр 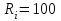 Ом. Решение системы осуществим с помощью системы MathCAD. Ом. Решение системы осуществим с помощью системы MathCAD.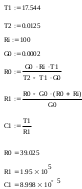 По справочнику [4] выберем в качестве 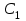 конденсатор типа К50-6-100мкФ с номинальной емкостью 100 мкФ. По справочнику [5, табл.2.2, стр. 20; табл. стр.83] выберем в качестве конденсатор типа К50-6-100мкФ с номинальной емкостью 100 мкФ. По справочнику [5, табл.2.2, стр. 20; табл. стр.83] выберем в качестве 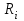 резистор МЛТ с номиналом 100 Ом, в качестве резистор МЛТ с номиналом 100 Ом, в качестве 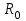 - резистор типа МЛТ с номиналом 40.2 Ом (ряд допусков Е96), в качестве - резистор типа МЛТ с номиналом 40.2 Ом (ряд допусков Е96), в качестве 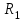 - резистор типа МЛТ с номиналом 196 кОм (ряд допусков Е96). - резистор типа МЛТ с номиналом 196 кОм (ряд допусков Е96).Постоянные времени КУ с учетом стандартных значений R и C: 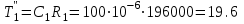 с с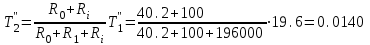 с с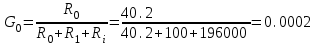 3.3 Структурно-параметрическая синтез оптимизированной САУ.Синтез будем проводить в соответствии с рекомендациями [3, стр. 253-256]. 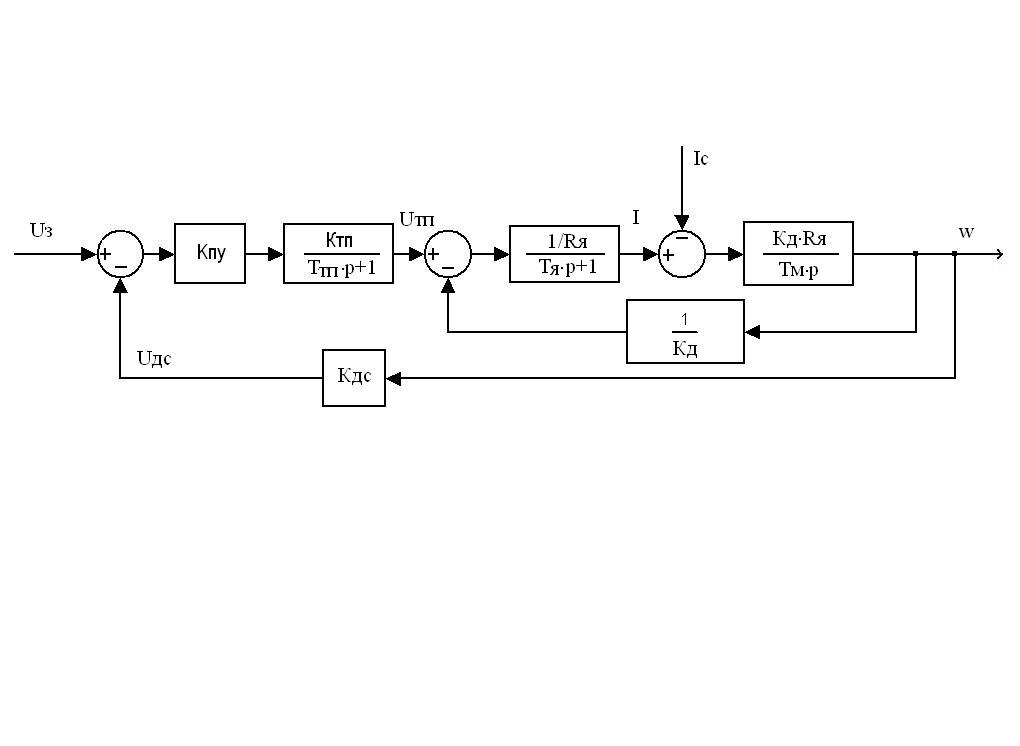 Выделим в схеме контуры подчиненного регулирования – внутренний (контур тока) и внешний (контур скорости). Кроме того, введем в схему ООС по току якоря (датчик тока) и регуляторы тока и скорости вращения.  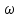 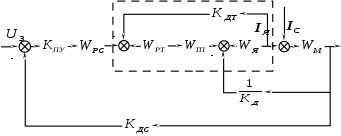 Пунктиром выделен контур тока. На данной схеме: 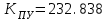 - коэффициент передачи предварительного усилителя; - коэффициент передачи предварительного усилителя; 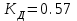 (рад/с)/В – коэффициент, характеризующий двигатель; (рад/с)/В – коэффициент, характеризующий двигатель; 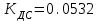 В/(рад/с) – коэффициент передачи датчика скорости; В/(рад/с) – коэффициент передачи датчика скорости; 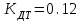 В/А – коэффициент передачи датчика тока. В/А – коэффициент передачи датчика тока.Передаточные функции звеньев схемы: 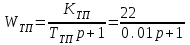 - передаточная функция тиристорного преобразователя; - передаточная функция тиристорного преобразователя;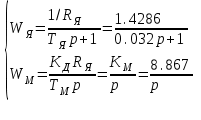 - передаточные функции, характеризующие электрические и механические свойства двигателя; - передаточные функции, характеризующие электрические и механические свойства двигателя;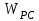 - искомая передаточная функция регулятора скорости; - искомая передаточная функция регулятора скорости;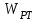 - искомая передаточная функция регулятора тока якоря. - искомая передаточная функция регулятора тока якоря.В контуре тока объектом управления является инерционное звено 2-го порядка: 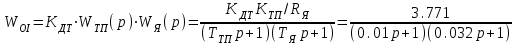 . .В соответствии с [3, стр. 247, табл. 7.2] целесообразным является применение ПИ-регулятора, настроенного по критерию модульного оптимума (МО), т.е. с полной компенсацией наибольшей постоянной времени ОУ, т.е. 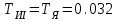 с. с. Передаточный коэффициент регулятора [3]: 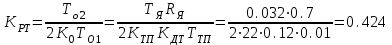 В/В В/ВТаким образом: 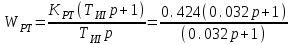 При выбранных настройках достигается компенсация 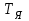 и эквивалентная ПФ замкнутого контура тока зависит только от и эквивалентная ПФ замкнутого контура тока зависит только от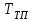 и равна и равна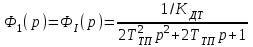 В соответствии с рекомендациями [3, стр. 255] членом 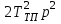 можно пренебречь из-за малости можно пренебречь из-за малости 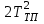 . Таким образом: . Таким образом: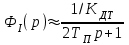 Контур тока является внутренним для контура скорости. С учетом последнего приближения объект регулирования в контуре скорости можно представить как: 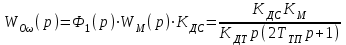 Данным ОУ можно управлять при помощи настроенного на СО ПИ-регулятора [3, стр. 247, табл. 7.2] вида [3, стр. 248, ф. 7.45]: 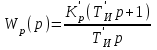 с коэффициентом передачи: 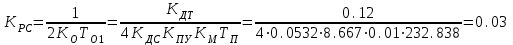 В/В В/Ви постоянной времени: 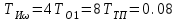 с. с.Таким образом: 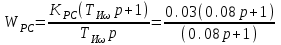 Однако, согласно [3, стр. 256] в этом случае будут возникать значительные перерегулирования, в этом случае в схему требуется включить сглаживающий фильтр [3, стр. 252, ф. 7.69] вида: 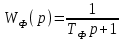 Постоянная времени фильтра: 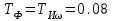 с. с.Схемная реализация ПИ-регуляторов будет выглядеть следующим образом [6, стр. 149-150]: 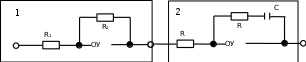 В этой схеме звено 1 реализует требуемые значения 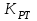 и и 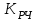 , а звено 2 – соответственно , а звено 2 – соответственно 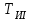 и и 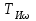 . Для подобной схемы ( в общем виде): . Для подобной схемы ( в общем виде):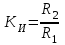 ; ; 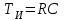 Таким образом, не составляет труда подобрать соответствующие схемные элементы. 4. Анализ синтезированных САУ.В качестве критериев анализа примем устойчивость  синтезированных систем, их запасы устойчивости по модулю и фазе и показатели качества переходных процессов. синтезированных систем, их запасы устойчивости по модулю и фазе и показатели качества переходных процессов.4.1 Анализ синтезированной САУ при последовательной коррекции.Построим ЛАЧХ скорректированной системы (в MATLAB): >> W=tf ([0 0 0 155.333],[0.0000144 0.00189 0.055 1]) Transfer function: 155.3 ----------------------------------------- 1.44e-005 s^3 + 0.00189 s^2 + 0.055 s + 1 >>wku=tf([0.0124 1], [17.4 1]) Transfer function: 0.0127 s + 1 ------------ 17.83 s + 1 >>Wsk=W*wku Transfer function: 1.973 s + 155.3 ------------------------------------------------------ 0.0002567 s^4 + 0.03371 s^3 + 0.9824 s^2 + 17.88 s + 1 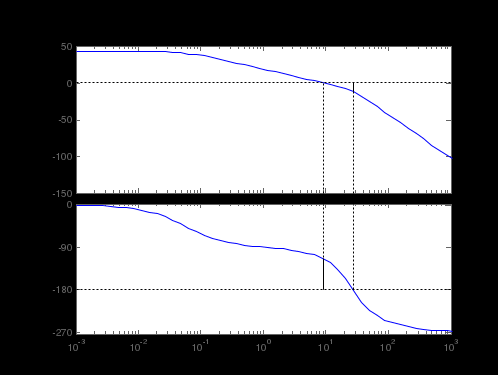 Видно, что после применения КУ система устойчива и имеет удовлетворительные запасы устойчивости по модулю и фазе. Оценим показатели качества переходных процессов в скорректированной системе. Для этого воспользуемся системой MATLAB. а) Канал управления. 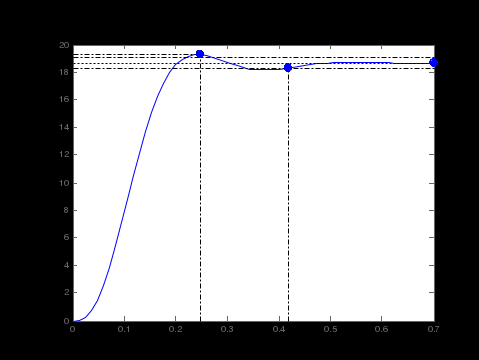 Видно, что время переходного процесса составляет 0.41 с, что значительно меньше допустимого значения 0.7 с. Перерегулирование составляет 1.6%. б) Возмущающее воздействие. 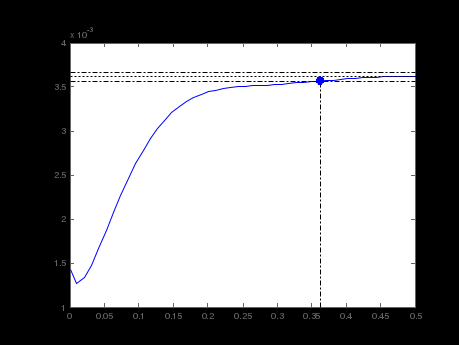 Видно, что длительность переходного процесса составляет 0.36 с, что меньше допустимого. Перерегулирование равно 0. Таким образом, данное последовательное КУ обеспечивает устойчивость исходной системы, приемлемые запасы устойчивости и отличные показатели качества при относительной простоте реализации КУ. 4.2 Анализ синтезированной САУ при параллельной коррекции.Проверим запасы устойчивости скорректированной САУ. ПФ скорректированной САУ будет иметь вид: 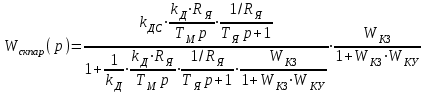 , ,где 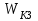 - ПФ корректируемых звеньев, - ПФ корректируемых звеньев, 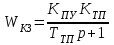 ; ;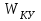 - ПФ корректирующего устройства, - ПФ корректирующего устройства, 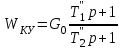 . .Построение (с учетом всех параметров) осуществим в MATLAB. 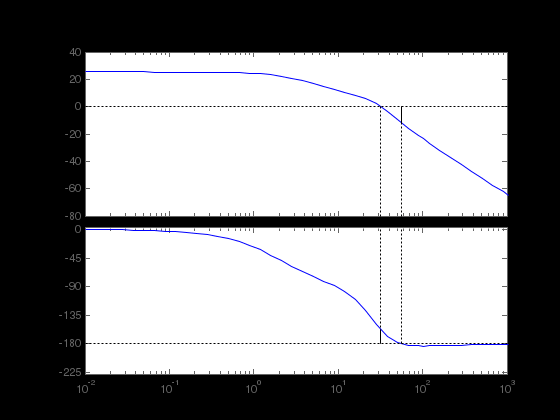 Запасы устойчивости составляют 12 дБ по амплитуде и 21.9 град по фазе. Построим переходную характеристику: 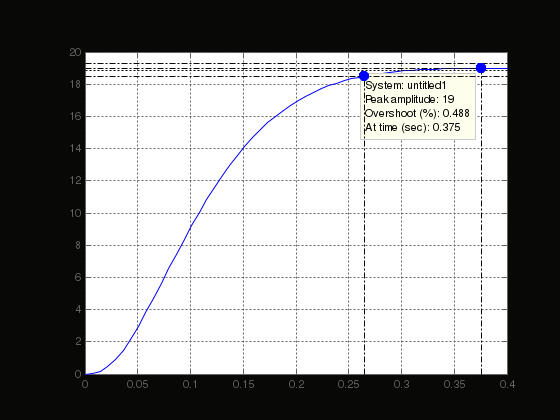 Время переходного процесса составляет 0.26 с, перерегулирование – 0.488 %. По возмущающему воздействию: 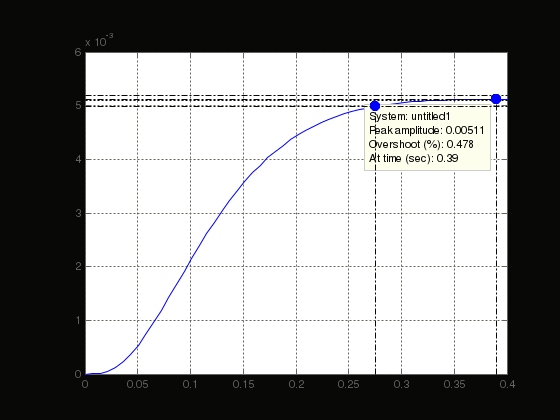 Время переходного процесса – 0.39 с, перерегулирование – 0.478 % 4.3 Анализ синтезированной САУ при структурно-параметрической оптимизации.За основу при построении характеристик примем расчет из п. 3.3. Осуществив построение в системе MATLAB, получим ЛАФЧХ скорректированной разомкнутой системы: >>Wtp=tf([0 22],[0.01 1]) Transfer function: 22 ---------- 0.01 s + 1 >>Wya=tf([0 1.4286],[0.032 1]) Transfer function: 1.429 ----------- 0.032 s + 1 >> Wm=tf([0 8.867],[1 0]) Transfer function: 8.867 ----- s >>kpu=232.838 kpu = 232.8380 >>kd=0.57 kd = 0.5700 >>kds=0.0532 kds = 0.0532 >>kdt=0.12 kdt = 0.1200 >> WOI=kdt*Wtp*Wya Transfer function: 3.772 ------------------------- 0.00032 s^2 + 0.042 s + 1 >> TI=0.032 TI = 0.0320 >>Kpt=0.424 Kpt = 0.4240 >> FI=tf([0 1/kdt],[0.02 1]) Transfer function: 8.333 ---------- 0.02 s + 1 >>Wpc=tf([0.03*0.08 0.03],[0.08 1]) Transfer function: 0.0024 s + 0.03 --------------- 0.08 s + 1 >>Wf=tf([0 1],[0.08 1]) Transfer function: 1 ---------- 0.08 s + 1 >>km=8.867 km = 8.8670 >>Wraz=Wf*Wpc*Wow Transfer function: 0.001132 s + 0.01415 ----------------------------------------------- 1.536e-005 s^3 + 0.001152 s^2 + 0.0216 s + 0.12 >>margin (Wraz) 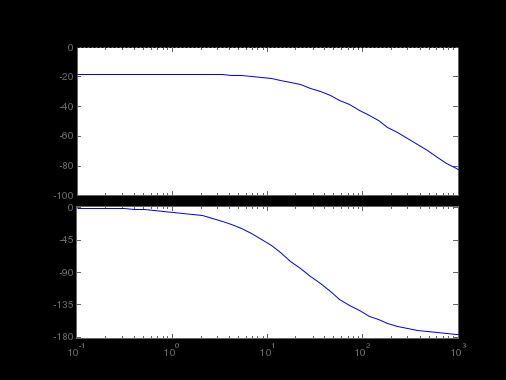 Видно, что система, подвергнутая структурно-параметрической оптимизации, абсолютно устойчива в широком диапазоне частот. а) Канал управления. 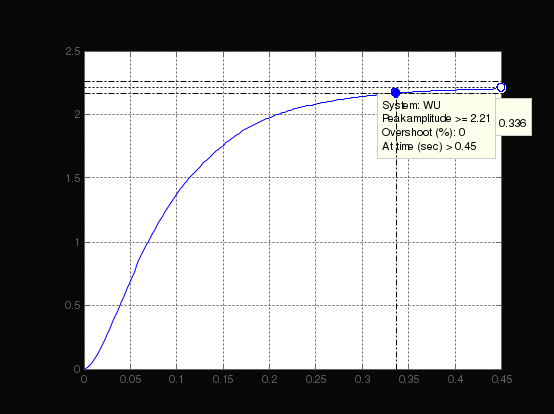 Время переходного процесса равно 0.336 с, перерегулирование равно 0%. б) Канал возмущения 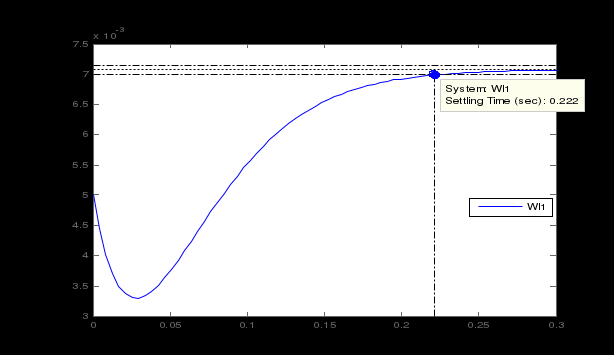 4.4 Сравнительный анализ различных способов коррекции.
Из таблицы видно, что наилучшими характеристиками обладает система, синтезированная по методу структурно-параметрической оптимизации. Недостатком данного способа является сравнительно сложная реализация регуляторов. 5. Библиографический список Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бесекерского - М. «Наука» 1972. Башарин А.В. , Голубев Ф.Н., Кепперман В.Г. Примеры расчета автоматизированного электропривода. - Л. «Энергия». 1972. Лукас В.А. «Теория автоматического управления» - . М.: «Недра»,1990. – 416 с. Конденсаторы: Справочник / И.И. Четвертаков, М.Н. Дьяконов, В.И. Присняков и др.: Под ред. И.И. Четвертакова, М.Н. Дьяконова – М.: Радио и связь, 1993. – 392 с. Резисторы: Справочник / В.В. Дубровский, Д.М. Иванов, Н.Я. Пратусевич и др.; Под ред. И.И. Четверткова и В.М. Терехова. – 2-е изд., перераб. и доп. – М.: Радио и связь, 1991. – 528 с. Терехов В. М. «Элементы автоматизированного электропривода» - М.: Энергоатомиздат, 1987. – 224 с. | |||||||||||||||||||||||||||||||||