Подборка стохастических задач по математике в начальной школе. Синяя коробка
 Скачать 135.41 Kb. Скачать 135.41 Kb.
|
|
Задание 1: У Кати 6 карандашей и 2 коробки: синяя и красная. Как она может разложить карандаши в эти коробки? Сколько различных вариантов распределения карандашей по коробкам ты насчитал? Проверь себя с помощью таблицы.
ОТВЕТ: 7 вариантов.
Задание 2: К праздничному вечеру ученики класса принесли воздушные шары – белые и синие, всего 8 шаров. Сколько среди них может быть синих шаров? Заполни таблицу и проверь себя с ее помощью.
ОТВЕТ: Задача решается методом систематического перебора. Синих шаров может быть 1,2,3,4,5,6,7 (см. таблицу)
Задание 3: На уборку пришли 9 учеников (мальчиков и девочек) второго «А» класса. Сколько может быть среди них мальчиков, а сколько девочек? Проверь себя с помощью таблицы.
ОТВЕТ: может быть: 8 мальчиков и 1 девочка, 7 мальчиков и 2 девочки и т.д.
Задание 4: Сколькими способами можно разложить 7 яблок на 2 тарелки? Проверь себя с помощью таблицы.
ОТВЕТ: 8 способов
Задание 5: Сколько сумм можно составить, если первое слагаемое выражения – число 1,5 или 8, а второе – число 4 или 6? ОТВЕТ: 6 различных сумм. Задание 6: Какие двухбуквенные слоги (согласная, гласная) можно составить из букв Б, Д, М, И, У? Назови все варианты.  ОТВЕТ: воспользуемся графом.  Задание 7: Брат и сестра собирают вещи для поездки в летний загородный лагерь. Брат берёт с собой 5 вещей: 2 брюк и 3 рубашки, сестра – тоже 5 вещей: 3 юбки и 2 кофты. Сестра говорит, что из своих вещей она сможет составить больше костюмов, чем брат. Права ли сестра? ОТВЕТ: сестра права. 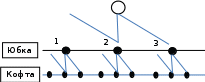 Задание 8: В соревнованиях «Моя спортивная семья» за общество синих выступают две мамы, два папы и трое детей. Сколькими способами можно сформировать команду, состоящую из одной мамы, одного папы и одного ребёнка? ОТВЕТ: 12 способов.  Задание 8: На рисунке точками А, В, С, Д обозначены четыре города. Линиями нарисованы дороги, которые соединяют эти города. Сколько существует способов попасть из города А в город Д?   ОТВЕТ: 12 способов. Задание 9: Буратино, Пьеро и Мальвина хотят выстроиться в ряд. Сколько вариантов у них может получиться? Ответ: 6 способов. Задание 10: Расположи в различном порядке слова: «нам», «нравится», «учиться». Сколькими способами можно сделать? НАМ НРАВИТСЯ УЧИТЬСЯ ОТВЕТ: 6 способов. Задание 11: Катя, Петя и Вова хотят занять 3 места в кабине «Колеса обозрения». Сколько различных комбинаций они могут использовать? ОТВЕТ: 6 способов. Задание 12: У Пьеро есть пластилин жёлтого, синего и красного цвета. Из него он решил вылепить большие и маленькие пластилиновые шарики, кубики и пирамидки. Сколько различных геометрических фигурок разных цветов он может сделать? ОТВЕТ: 18 геометрических фигурок. (комбинаторная таблица)
Задание 13: У Наташи 3 куклы, 2 мяча и 3 мягкие игрушки. Она хочет выбрать из этих игрушек 1 куклу, 1 мяч и 1 мягкую игрушку. Сколько вариантов выбора возможны? ОТВЕТ: 18 способов. Задание 19: У старухи Шапокляк есть туфли на высоком каблуке и туфли на низком каблуке, четыре шляпки разного цвета и два плаща (один длинный, другой короткий). Сколько у неё может быть вариантов одеться по-разному, чтобы удивить своих знакомых? ОТВЕТ: 16 вариантов. Задание 20: В школьном буфете на первое можно заказать суп, борщ, щи, на второе – пюре и салаты, на третье – чай и компот из сухофруктов. Сколько различных вариантов обеда можно составить из указанных блюд? ОТВЕТ: 12 вариантов. Задание 21: На скамейку хотят сесть три девочки: Алиса, Вероника и Марина. Сколькими различными способами они могут сесть рядом? ОТВЕТ: 6 способов. Задание 22: Для поднятия флага соревнований нужно выбрать двух школьников из четырёх. Сколькими различными способами это можно сделать? О  ТВЕТ: 6 способов. Каждая линия – это выбранные два школьника. ТВЕТ: 6 способов. Каждая линия – это выбранные два школьника.З  адание 23: Есть три квадрата: синий, серый и голубой. Сколькими способами можно выбрать два квадрата их этих трёх? адание 23: Есть три квадрата: синий, серый и голубой. Сколькими способами можно выбрать два квадрата их этих трёх? ОТВЕТ: 3 способа. Задание 24: Перед тобой 5 одинаковых полосок: 2 синих и 3 зелёных. Из них нужно составить прямоугольник (см.ниже) . Сколько различных прямоугольников ты сможешь составить? ОТВЕТ: 10 вариантов.  Задание 25: Сколько квартетов можно составить из 6 музыкантов? ОТВЕТ: 15 квартетов. Петя отметил на окружности 7 точек и соединил каждые две точки отрезками. Сколько отрезков получилось? ОТВЕТ: 21отрезок. Решение: Из первой точки можно провести 6 отрезков, из второй- 5, из третьей- 4, из четвёртой – 3, из пятой – 3, из шестой – 1 отрезок. Следовательно, всего петя провёл 6+5+4+3+2+1=21(от) Задание 26: Запиши все двузначные числа, которые можно составить из цифр 2,4,7,8, так, чтобы число десятков было больше числа единиц. ОТВЕТ: 6 чисел. Типовые задания Задание 1. Продолжите фразу: Букет – это множество … Стая – это множество … Сервиз – это множество… Примечание: В задании 1 о множестве говорится в явном виде. Задание 2. Дайте названия множествам: Груша, яблоко, банан, абрикос, апельсин; Берёза, клён, осина, дуб, сосна; Тюльпан, нарцисс, ромашка, гвоздика, колокольчик; Треугольник, квадрат, прямоугольник, круг. Задание 3. Назовите группу чисел одним словом: а) 2; 4; 7; 9; 6 _________________. б) 18; 25; 33; 48; 57 _______________. в) 231; 564; 872; 954 _________________. Элементы математической логики Обучение решению логических задач в начальной школе включает в себя: - понимание смысла логических связок-слов «и», «или», «не», «если …то»; - понимание смысла кванторных слов «все», «ни один», «каждый», «некоторый»; - построение несложных составных высказываний с вышеназванными словами и определение их истинности; - умение проводить классификацию, сравнение, аналогию, сериацию и т.д. Без логических операций невозможно полноценное усвоение курса математики, именно слова логических операций служат основой формирования умений решать текстовые задачи. В процессе решения логических задач у младших школьников развиваются следующие логические УУД: построение логической цепи рассуждений, доказательств, выдвижение гипотез и их обоснование. Типовые задания Задание 1. Выделите 2 слова из скобок, наиболее существенные для слова, стоящего перед скобками: Сад (растение, садовник, собака, забор, земля); Река (берег, рыба, тина, рыболов, вода); Куб (углы, чертёж, сторона, камень, дерево); Чтение (глаза, книга, картина, печать, слово); Игра (шахматы, игроки, штрафы, правила, наказания). Задание 2. Выпишите черты сходства – слева, а справа – черты различия названных предметов или понятий: книга – тетрадь, солнце – луна, лошадь – корова, сани – телега, линейка – треугольник, дождь – снег. Задание 3. Аня, Женя, Нина спросили, какие оценки им поставили за контрольную работу по математике. Учитель ответил: «Плохих оценок нет. У вас троих оценки разные. У Ани не «3». У Нины не «3» и не «5». Кто какую оценку получил? Задание 4. 1) Даны числа 1; 2; 3; 4; 5; 6; 7; 8; 9; 10. Раздели их на две группы: а) четные; б) нечетные. 2) Даны числа 2; 13; 3; 43; 6; 55; 18; 7; 9; 31. Раздели на две группы: а) однозначные; б) двузначные. 3) Числа 22; 35; 48; 51; 31; 45; 27; 24; 36; 20 разбиты на 2 группы: четные и нечетные. На какой строчке классификация проведена правильно? а) 31; 35; 27; 45; 51; 22 48; 24; 20; 36. б) 3; 35; 27; 45; 51 27; 20; 24; 36; 22; 48. в) 27; 31; 35; 45; 51 20; 24; 22; 36; 48. г) 26; 31; 36; 35; 45; 51 20; 24; 22; 48. Задание 5. Какие из данных предложений истинны (верны), а какие ложны (не верны): Число 24 – чётное 3+3 = 33 56 < 102 45:5 =11? Задание 6. В каком случае предложения будут истинны? Если на улице весна, то на деревьях распускаются листья. Если на улице холодно, то идёт снег. Среди вас есть хотя бы один, кто летал на самолёте. У всех девочек вашего класса длинные волосы. Элементы комбинаторики Комбинаторные задачи включены в программу по математике, начиная в первого класса, они формируют у обучающихся представления: - о комбинаторном соединении, - об основных видах комбинаторных соединений (перестановка, размещение, сочетание). В ходе решения комбинаторных задач у младших школьников формируются следующие предметные УУД: умение работать с таблицами, графами и граф-деревьями, применять правила суммы и произведения. При выполнении заданий такого вида учащиеся осваивают смысловое чтение и действия, связанные с поиском и выделением информации, моделированием. Комбинаторные задачи служат эффективным средством для формирования умений сравнивать и классифицировать объекты, строить логические цепочки рассуждений, а также способствуют развитию монологической и диалогической речи обучающихся в соответствии с нормами родного языка; инициативного сотрудничества в процессе поиска и сбора информации. Типовые задания Задание 1. Составьте из цифр 1, 3, 7 все возможные трёхзначные числа так, чтобы цифры в числе не повторялись. Задание 2. Из цифр 2, 7, 3 составьте все возможные двузначные числа (цифры могут в числе повторяться). Сколько и какие из них больше 30? Задание 2. У кошки Мурки родилось 8 котят. Из них 6 – пушистые, а 5 – рыжие. Может ли быть такое? Сколько одновременно рыжих и пушистых котят у Мурки? Задание 4. Начертите отрезок АО. Поставь внутри него 3 точки, обозначь их буквами С, М, К. Сколько всего получится отрезков? Задание 5. У Леры имеется 4 вида цветной бумаги (красная, синяя, желтая и зелёная) и 3 вида образца оригами животных (кошка, собака, колибри). Сколько вариантов одного любого животного она может сделать из любого цвета? Задание 6. Из города А в город В ведут шесть дорог, а из города В в город С — пять дороги. Сколько путей, проходящих через В, ведут из А в С? Задание 7. Пять подружек после отдыха в летнем лагере обменялись фотографиями на память (каждая подарила остальным одну свою). Сколько фотографий потребовалось? Задание 8. У Влады в четверг 2 лёгких предмета – физкультура и изо, и 2 трудных предмета – русский и математика. Как нужно составить расписание, чтобы лёгкие предметы чередовались с трудными? Найдите все варианты. Элементы теории вероятностей направлены на: - формирование представлений о том, что такое событие и его вероятность; - знакомство с видами событий и способами нахождения простейших вероятностей. Эти задания знакомят с основными видами событий, такими как достоверные, невозможные, случайные, противоположные, совместные и несовместные, зависимые и независимые. При выполнении таких заданий младшие школьники учатся проводить простой эксперимент с различными исходами, находить простейшие вероятности. Такая работа направлена на формирование следующих метапредметных УУД: ставить учебную задачу на основе имеющихся знаний, соотнесения границ известного и ещё неизвестного; составлять план и определять последовательность действий; прогнозировать, предвосхищать результат [7]. Типовые задания Задание 1. Какое из названных событий обязательно произойдет, какое невозможно, какое маловероятно, а какое примерно в равной степени может быть, а может и не быть: урок математики длится 30 мин; наугад названный ряд год равен 366 суткам; 20 мин длятся дольше 1200 с; После понедельника будет среда; После субботы будет воскресенье. Задание 2. В коробке находятся 2 белых и 2 черных шара. Наугад взяли один шар. Какого цвета он может быть? Наугад взяли 2 шара. Могут ли шары оказаться одного цвета? Разного цвета? Наугад взяли 3 шара. Могут ли они быть одного цвета? Какие возможны варианты [2, с.34]. Задание 3. Ученик первого класса отвлёкся и из содержания задачи услышал только два числа. Он сложил их и записал таким образом решение задачи. Могло ли оказаться, что действие он выбрал правильно? Задание 4. Если подбросить монету, то может выпасть орёл или решка. Что может выпасть, если подбросить 2 монеты? Элементы математической статистики Математические задачи с элементами статистики в начальной школе формируют у обучающихся представления: - о статистических данных, - об основных видах записи статистических данных (таблицы, диаграммы), - о некоторых числовых характеристиках статистических данных. В процессе их решения младшие школьники осуществляют сбор данных эксперимента и учатся записывать их в таблицу, овладевают приемами поиска необходимой информации в простейших таблицах, построения и чтения простейших круговых, столбчатых диаграмм, нахождения некоторых выборочных характеристик (объема данных, моды, медианы, размаха, среднего арифметического нескольких чисел). Познавательные УУД формируются в ходе работы по преобразованию текстов, таблиц, схем, диаграмм, сопоставлению информации, представленной в разных формах. Типовые задания Задание 1. Составьте таблицу данных о росте обучающихся класса, в которую нужно занести только отличающиеся значения роста и число детей, имеющих такой рост. Есть ли у вас в классе дети с одинаковым ростом? Какой рост самый «популярный» в вашем классе? Какова наибольшая разница в росте? Каков средний рост обучающихся в классе? У какого количества обучающихся рост выше среднего? Ниже среднего? Равен среднему? Примечание: В математике такая таблица называется статистическим распределением ряда данных. Популярный рост – это мода ряда данных. Наибольшая разница – это размах ряда данных. Подобные задания, требующие сбора, упорядочивания, кодирования и сохранения в удобной форме информации об обучающихся класса, являются эффективным средством стохастической пропедевтики. Задание 2. Составьте по плану статистический отчёт о работе на уроке при подведении итога: Сколько всего вычислений выполнил каждый из вас в течение урока? Сколько пар чисел вы сложили, вычли, умножили и разделили за урок? Сколько раз на уроке вы выполняли сложение, вычитание, умножение, деление? Какое действие вы выполняли сегодня чаще (реже) других? Опыт каких вычислений на сегодняшнем уроке был большим? Задание 3. Подбросьте монету 20 раз. Заполните таблицу:
Совпадают ли результаты наблюдений с наблюдениями ваших одноклассников [2]? Решение стохастических задач связано с умениями «читать» информацию, представленную в разных формах, работать с таблицами, анализировать данные, строить логические рассуждения, проводить умозаключения, классифицировать, сравнивать, находить существенные признаки, делать выводы, которые составляют познавательные УУД. Совместная работа младших школьников, работа в парах при решении стохастических задач способствует формированию правил поведения в группе, умений распределять функции и соблюдать очередность действий, слушать точку зрения партнера, правильно формулировать вопрос, организовывать взаимопроверку, высказывать свое мнение при обсуждении задания и его решении, прислушиваться к мнению других и доносить до них свою точку зрения, т.е. формированию личностных и коммуникативных УУД. Введение стохастических задач в курс математики начальной школы позволит развивать математическую интуицию, логику и математическую грамотность. Понятия и методы стохастической линии могут использоваться обучающимися как средства описания окружающей действительности и решения конкретных практических задач. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 игура
игура