Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; з. Документ Microsoft Word (2). Система работы по формированию навыков решения текстовых задач. Лескевич Тамара Иосифовна, учитель математики Содержание
 Скачать 209.2 Kb. Скачать 209.2 Kb.
|
|
Задача 6 Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди? . Изобразим сплавы в виде прямоугольников М С М С + = х(г) (200 –х) (г) 200 (г) 0,15х + 0,65(200 – х) = 0,3 *200 х = 140 2. Обозначим М С М С + = х(г) у(г) 200(г) Ответ: 140г меди и 60г свинца Задача 7 Имеются сплавы золота и серебра. В одном эти металлы находятся в отношении 2: 3, а в другом в отношении 3: 7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11? 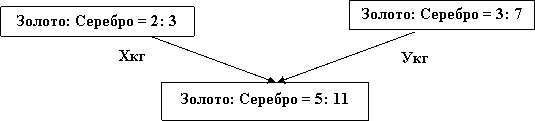 По этой схеме уравнение х + у =1 показывает массу нового сплава. Определяем массу золота в каждом сплаве и получаем уравнение Аналогично массу серебра и получаем уравнение * х + * у = * 1 Записываем одну из систем: Решая ее, получаем х = 0,125 и у = 0,875 Ответ: 125 г и 875 г. Приложение 6 Нестандартные способы решения задач на смеси и сплавы. Задача 1. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%?  Ответ: 7 килограммов. Задача 4. Из сосуда, доверху наполненного 97% раствором кислоты, отлили 2 литра жидкости и долили 2 литра 45% раствора этой же кислоты. После этого в сосуде получился 81% раствор кислоты. Сколько литров раствора вмещает сосуд? Задача 5. Смешали 500 г 10%-го раствора соли и 400 г 55%-го раствора соли. Определите концентрацию соли в смеси. Задача 6. Имеются два слитка, содержащие медь. Масса второго слитка на 3 кг больше, чем масса первого слитка. Процентное содержание меди в первом слитке – 10%, во втором – 40%. После сплавления этих двух слитков, получился слиток, процентное содержание меди в котором 30%. Определить массу полученного слитка. Задача 7. Сплавили 300 г сплава олова и меди, содержащего 60% олова, и 900г сплава олова и меди, содержащего 80% олова. Сколько процентов олова в получившемся сплаве? Задача 8. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? Ответ: 5%. Задача 9. Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? Ответ: 17%. Задача 10. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Ответ:21%. Задача 11. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Ответ: на 100 кг. Задача 12. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. Задача 13. По дороге ТУДА Винни Пух нашел дупло с мёдом. По его ощущениям этот мёд, к сожалению, только лишь на одну пятую часть правильный (остальные четыре пятые – неправильные). В дупле же, найденном по дороге ОБРАТНО, мёд на 60% правильный. Сколько килограммов мёда нужно взять из первого и второго(10 – Х) кг дупла, чтобы в общей сложности получить 10 кг меда, содержащего 32% правильного? Задача 6. Имеются два слитка, содержащие медь. Масса второго слитка на 3 кг больше, чем масса первого слитка. Процентное содержание меди в первом слитке – 10%, во втором – 40%. После сплавления этих двух слитков, получился слиток, процентное содержание меди в котором 30%. Определить массу полученного слитка. Задача_Имеется_два_сплава_меди_и_олова._Один_сплав_содержит_72%_меди,_а_другой_80%_меди._Сколько_нужно_взять_каждого_сплава,_чтобы_получилось_800г_сплава,_содержащего_75%_меди'>Задача Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800г сплава, содержащего 75% меди? Друг под другом пишутся процентные содержания меди в имеющихся сплавах, слева от них и примерно посередине – процентное содержание меди в сплаве, который должен получиться после сплавления. Соединив написанные числа черточками, получим такую схему: 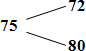 Рассмотрим пары 75 и 72; 75 и 80. В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей стрелочки. Получится такая схема: 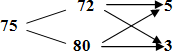 Из нее делается заключение, что 72%-ного сплава следует взять 5 частей, а 80%-ного – 3 части (800:(5 + 3) = 100 г приходится на одну часть.) Таким образом, для получения 800 г 75%-ного сплава нужно взять 72%-ного сплава 100·5 = 500 г, а 80%-ного – 100·3 = 300 г. Ответ:500г, 300г. Задача 1 Смешали некоторые количества 72%-ого и 58%-ого растворов кислоты, в результате получили 62%-й раствор той же кислоты. Если бы каждого раствора было на 15 л больше, то получили бы 63,25%-й раствор. Сколько литров каждого раствора было взято первоначально для составления первой смеси? Решение. Дважды используем диагональную схему: 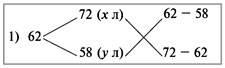 Получаем: 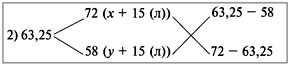 Получаем: Составим схему уравнений и решим её: Ответ:12 л 72%-ого и 30 л 58%-ого растворов. Задача Сплавили два слитка серебра: 75 г 600-й и 150 г 864-й пробы. Определить пробу сплава. Пусть проба сплава равна х. Составим диагональную схему: 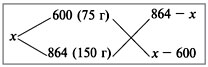 Получаем: (864 – х) : (х – 600) = 75 : 150 1728 – 2х = х – 600 х = 776. Ответ: сплав 776-й пробы. |
