Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; з. Документ Microsoft Word (2). Система работы по формированию навыков решения текстовых задач. Лескевич Тамара Иосифовна, учитель математики Содержание

• Название: Система работы по формированию навыков решения текстовых задач. Лескевич Тамара Иосифовна, учитель математики Содержание
• Анкор: Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; з
• Дата: 11.03.2022
• Размер: 209.2 Kb.
• Имя файла: Документ Microsoft Word (2).docx
• Тип: Документы; #392650
• страница: 3 из 5

Проценты и прибыль

Задача 4. Три человека организовали собственное предприятие и договорились, что первый из них будет получать третью часть прибыли, двое других по 20%, а остальные деньги они будут вкладывать в развитие своего предприятия. Сколько процентов от прибыли они будут вкладывать в развитие предприятия?

Решение:

Вся прибыль – 100%

1) 100/3=33,3% третья часть прибыли, получает первый предприниматель в процентах.

2) 20+20+33,3=73,3 (%) - от прибыли получают все предприниматели

3) 100-73,3=26,7% - от прибыли они будут вкладывать в развитие предприятия

Ответ: 26,7% от прибыли они будут вкладывать в развитие предприятия

Проценты в магазине

Задача 5. В течение недели магазин получил 60 000 р. дохода. Из них 15 000 р. от продажи продовольственных товаров. Сколько процентов составил доход от продажи непродовольственных товаров?

Решение:

За 100% принят доход – 60 000 рублей.

1) 60000:100=600(руб.) – составляет 1%

2) 60000-15000=45000 (руб.)- доход от непродовольственных товаров

В) 45000:600=75%

Ответ: 75% составил доход от продажи непродовольственных товаров?

Задача 6. Рекламный ролик стоил 1200 рублей, в сентябре цена на него повысилась на 10%, в ноябре упала на 20%. Сколько нужно заплатить за рекламный ролик сейчас.

Решение: Составим блок-схему

?
10% 20%
1200 р

?


1. 10%∙1200=0,1∙1200=120(р) – составляет 10%

2. 1200+120= 1320(р) – цена после повышения.

3. 20%∙ 1320= 0,2∙1320=264(р) – составляет 20%

4. 1320-264= 1056(р)- новая цена.

Ответ: 1056 рублей.

Приложение 4

7. 
   Решение задач на вычисление сложных процентов:
   

Этот блок составлен из самых сложных практически значимых задач, для решения задач данного типа необходимо использовать формулу для вычисления сложных процентов, которая не рассматривается в школьном курсе алгебры. Этот вид задач рассматривается с учащимися при подготовке к олимпиаде.

С = х (1+а%)ⁿ,

где С – новая цена

х – первоначальная цена

а - ежемесячная процентная ставка

n – срок вклада (количество месяцев)

При решении данных задач первоначально следует разобраться в сложном запутанном условии задачи. Отвечая последовательно на вопросы, задача становится более понятной и доступной для решения.

Вопросы:

1. 
   Сколько объектов (фирм, магазинов…) описывается в условии задачи;
   
2. 
   а) Определить процент повышения (понижения) цен на первом объекте;
   

б) Сколько месяцев подряд происходило повышение (понижение) цен на первом объекте;

3. 
   а) Определить процент повышения (понижения) цен на втором объекте;
   

б) Сколько месяцев подряд происходило повышение (понижение) цен на втором объекте;

4. Какое условие задачи является связующим звеном п.2 и п.3;

5. Применить формулу сложных процентов для нахождения цен на обоих объектах.

Составленная блок-схема значительно поможет ответить на вопросы и разобраться в условии.

Задача №1. Число 51,2 трижды увеличивали на одно и тоже число процентов, а затем трижды уменьшали на одно и тоже самое число процентов. В результате получилось число 21,6. На сколько процентов увеличивали, а затем уменьшали эточисло?

Решение.

По формуле Аn=A₀(1+P/100)ⁿ

A₀=51, 2

N=3

P- неизвестно

51,2(1+P/100)³ - такое число стало после трёхкратного увеличения, т. е. это А3

затем это число А3 уменьшали трёхкратно на Р% и получили

51,2(1+Р/100)³ ∙ (1-P/100)³ – по условию это выражение равно21,6

51,2(1+Р/100)³ ∙ (1-Р/100)³ =21,6 это уравнение относительно Р

((1+Р/100)(1-Р/1000))³=27/64;

(1-(Р/100)²)³=(3/4)³;

1-(Р/100)²=3/4;

(P/100)²=1-3/4;

(P/100)²=1/4;

P/100=1/2;

P=50

Значит, число процентов равно 50.

Ответ: 50%.
Задача №2 Цену товара сначала снизили на 20% , затем новую цену снизили ещё на 15% и, наконец, после перерасчета произвели снижение ещё на 10% . Какова новая цена товара, если первоначальная цена 2500р.

Решение:

1.По формуле «сложных процентов»

А3=Ао∙(1-Р1/100)∙(1-P2/100)∙(1-P3/100)

А3=А0∙ (1-20/100) ∙ (1-15/100) ∙ (1-10/100)

A3=A0∙4/5∙17/20∙9/10

A3=2500∙4∙17∙9/1000

A3= 612∙2, 5

A3= 1530

1530р. – новая цена, т. е. цена снизилась на 970р.

Ответ: 1530 р.

2.Решим эту же задачу обычным способом ( по определению процента)

1)2500∙0,2=500(руб.) – на столько снизили цену в 1-й раз

2)2500-500=2000 (руб.) – новая цена после 1-го снижения её на 20%.

3)2000∙0,15= 300 (руб.) на столько снизилась цена во 2-ой раз.

4) 2000-300=1700(руб.) – новая цена после её снижения на 15%.

5) 1700∙0.1=170 (руб.) на столько снизилась в 3-й раз

6)1700-170=1530 (руб.) – новая цена после её снижения на 10 %

Ответ: 1530 руб.

Задача №4. В 1-ый день продали 40% всех яблок, во 2-й день – 20% остатка, а в 3-й день – 50% оставшихся яблок. Сколько всего продали кг яблок, если первоначально их было 1200кг.

Решение:

1. По формуле «сложных процентов»

Аn=A₀∙ (1-40/100) ∙ (1-20/100) ∙ (1-50/100)

An=1200∙6/10∙8/10∙1/2

An=1200∙24/100=12∙24=288(кг)

Ответ: 288кг

2. По определению процента.

1) 1200 ∙ 0.4=480(кг) яблок продали в 1-й день.

2)1200-480=720(кг) яблок осталось в 1-й день.

3)720∙0.2=144(кг) яблок продали во 2-ой день.

4)720-144=576(кг) осталось во 2-ой день

5) 576∙0.5=288(кг) – осталось в 3-й день.

Ответ: 288 кг

Задача №5. Рыночная цена картофеля в связи с переменной погодой понизилась на 25%, затем повысилась на 20%, потом вновь понизилась на 10%, а весной повысилась на 20%.Выросла ли цена по сравнению с первоначальной, или понизилась и на сколько?

Решение: Пусть Ао - первоначальная цена, а Аn – полученная цена, решаем по формуле сложных процентов

Аn=Aо∙ (1-25/100) ∙ (1+20/100) ∙ (1-10/100) ∙ (1+20/100)

An=Aо∙ (1-1/4) ∙ (1+1/5) ∙ (9/10) ∙11/5

An=Aо∙3/4∙6/5∙9/10∙6/5

An=Aо∙972/1000

Т.к. 972/1000<1,то Anо,

Т.е. новая цена стала меньше

Найдем разницу в процентах ( Aо-An)/Aо∙100%= (Aо-972/1000∙Aо)/Aо∙100%=

=(1-972/1000)*100%= 100% - 97,2%=2,8%

Цена стала меньше на 2,8% Ответ: на 2,8%
7.Решение задач на смеси и сплавы.

В условиях задач «на сплавы» и «на смеси» речь идет о составлении сплавов, растворов или смесей двух или нескольких веществ.

В процессе решения таких задач используется понятие «концентрации вещества», т.е. доли этого вещества в массе или объеме сплава (смеси, раствора).

концентрация раствора – отношение массы чистого вещества (твёрдого вещества) к массе всего раствора . Она показывает долю вещества в растворе.

Процент - одна сотая любого вещества.

Текстовые задачи на смеси и сплавы при всей их кажущейся простоте часто вызывают проблемы при подготовке к ЦТ.
Решение задач I типа:

Все задачи этого типа объединяет один способ решения, на основании составленной блок-схемы, вводится неизвестная переменная, которой обозначается все множество, данное в условии; используя процентное соотношение, составляется уравнение.

Типичные ситуации Смешали две смеси

При образовании смеси складываются абсолютные содержания. Поэтому, если известны только относительные содержания, то нужно:

1. 
   подсчитать абсолютные содержания;
   
2. 
   сложить абсолютные содержания, то есть подсчитать абсолютные содержания компонент смеси;
   
3. 
   подсчитать относительные содержания компонент смеси.
   

Примеры решения задачи на смеси. Приложение 5

Решение задач II типа:

Все задачи этого типа объединяет также один способ решения, на основании составленной блок-схемы, вводятся неизвестные переменные х и у, где х – масса, взятого от первого куска, у – масса, взятого от второго куска. Используя процентное соотношение, составляется система уравнений, в которой первое уравнение выражает содержание одного из данных в условии веществ, входящих в состав слитка (сплава, раствора), а второе – другое вещество.

Составленная блок-схема облегчает понимание условия задачи и способствует правильному решению задачи на проценты.

Все вычисления производятся устно, без использования калькулятора, применяя рациональный (удобный) способ счета.

Задача 1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800г сплава, содержащего 75% меди?

Изобразим каждый из сплавов в виде прямоугольника, разбитого на два фрагмента по количеству входящих элементов. Кроме того на модели отобразим характер операции – сплавление. Для этого между первым и вторым прямоугольниками поставим знак «+», а между вторым и третьим прямоугольниками поставим знак «=». Этим мы показываем, что третий сплав получен в результате сплавления первых двух. Полученная схема имеет следующий вид:

Теперь заполним получившиеся прямоугольники в соответствии с условием задачи.
Над каждым прямоугольником укажем соответствующие компоненты сплава. При этом обычно бывает достаточно использовать первые буквы их названия (если они различны). Удобно сохранять порядок соответствующих букв.
Внутри прямоугольников впишем процентное содержание (или часть) соответствующего компонента. Если сплав состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго равно разности 100% и процентного содержания первого.
Под прямоугольником запишем массу (или объем) соответствующего сплава (или компонента).
Рассматриваемый в задаче процесс можно представить в виде следующей модели-схемы: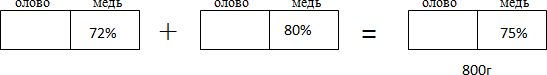



Решение.

1-й способ. Пусть х г – масса первого сплава. Тогда, (800 – х) г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему: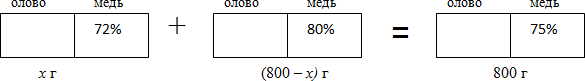



Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства): .

Решив это уравнение, получаем При этом значении х выражение . Это означает, что первого сплава надо взять 500 г, а второго – 300 г.

Ответ:500 г, 300 г.
2-й способ. Пусть х г и у г – масса соответственно первого и второго сплавов, то есть пусть исходная схема имеет вид:



Легко устанавливается каждое из уравнений системы двух линейных уравнений с двумя переменными:
Решение системы приводит к результату: Значит, первого сплава надо взять 500 г, а второго – 300 г.

Ответ:500 г, 300 г.
Нестандартные способы решения задач на смеси и сплавы.

При решении задач на смешивание растворов разных концентраций на факультативах использую диагональные схемы («правило креста»).

Пусть требуется приготовить раствор определенной концентрации. В распоряжении имеется два раствора с более высокой и менее высокой концентрацией, чем нужно.

Если обозначить массу первого раствора через m ₁, а второго – через m ₂, то при смешивании общая масса смеси будет складываться из суммы этих масс.

Пусть массовая доля растворённого вещества в первом растворе – ω ₁, во втором – ω ₂, а в их смеси – ω ₃. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах:

m ₁ ω ₁ + m ₂ ω ₂ = ω ₃(m ₁ + m ₂),

m ₁(ω ₁ – ω ₃) = m ₂(ω ₃ – ω ₂),

Очевидно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворённого вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.

При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения или квадрат Пирсона.

На диагональной схеме в точке пересечения двух прямых обозначают концентрацию смеси. У концов этих прямых слева от точки пересечения указывают концентрации составных частей смеси, а справа–разности концентраций смеси и её составных частей.

Рассмотрим применение диагональной схемы на общем примере:

В каких пропорциях нужно смешать a%-й и b%-й растворы кислоты (a < b), чтобы получить с%-й раствор?

Возьмем х г а%-го раствора и у г b%-го раствора кислоты. Составим таблицу:
Концентрация раствора,
%

Масса раствора,
г

Масса кислоты,
г

a

х

0,01ax

b

у

0,01by

c (смесь)

x + y

0,01c(x + y)

Составим и решим уравнение:

0,01ах + 0,01by = 0,01c(x + y),

(b – с)у = (с – а)х,

x : у = (b – с) : (с – а).

Воспользуемся диагональной схемой: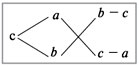



В этой схеме а и b – концентрации исходных растворов, с – требуемая концентрация кислоты в процентах, а «крест-накрест» – записаны их разности (b – с) и (с – а), соответствующие отношению масс растворов а и b.

Задача 1. Из сосуда, доверху наполненного 97% раствором кислоты, отлили 2 литра жидкости и долили 2 литра 45% раствора этой же кислоты. После этого в сосуде получился 81% раствор кислоты. Сколько литров раствора вмещает сосуд?

Решение:




Задача 2.Сплавили два слитка серебра: 75 г 600-й и 150 г 864-й пробы. Определить пробу сплава.

Решение. Пусть проба сплава равна x. Составим диагональную схему: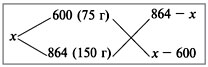



Получаем:

;





Ответ. Получили сплав 776-й пробы.

Примеры решения задач такого вида в Приложение 6

Данный метод может использоваться и при решения задач на смеси и сплавы. Отлили часть раствора, отрезали кусок сплава. При этой операции остается неизменной концентрация веществ.

Приложение 1

ОБЩАЯ СХЕМА РЕШЕНИЯ ЗАДАЧ

1. Нужно ясно понять задачу

Что неизвестно?

Что дано?

В чем состоит условие?

Возможно ли удовлетворить условию?

Достаточно ли условие для неизвестного?

Или недостаточно?

Или чрезмерно?

Или противоречиво?

Сделайте чертеж. Введите обозначения. Разделите условие на части. Постарайтесь записать их.

2. СОСТАВЛЕНИЕ ПЛАНА РЕШЕНИЯ.

Нужно найти связь между данными и неизвестным. Если не удается сразу обнаружить эту связь, возможно, полезно будет рассмотреть вспомогательные задачи. В конечном счете необходимо прийти к плану решения.

Не встречалась ли вам раньше эта задача?

Хотя бы несколько в другой форме?

Известна ли вам какая-нибудь родственная задача?

Не знаете ли теоремы, которая могла бы оказаться полезной?

Рассмотрите неизвестное! И постарайтесь вспомнить знакомую задачу с тем же или подобным неизвестным.

Вот задача, родственная с данной, и уже решенная.

Нельзя ли воспользоваться ею?

Нельзя ли применить ее результат?

Нельзя ли использовать метод ее решения?

Не следует ли ввести какой-нибудь вспомогательный элемент, чтобы стало возможно воспользоваться прежней задачей?

Нельзя ли иначе сформулировать задачу, еще иначе?

Вернитесь к определениям.

Если не удается решить данную задачу, попытайтесь сначала решить сходную.

Нельзя ли придумать более доступную сходную задачу?

Более общую?

Более частную?

Аналогичную?

Нельзя ли решить часть задачи?

Сохраните только часть условия, отбросив остальную часть: насколько определенным окажется тогда неизвестное!

Как оно сможет меняться?

Нельзя ли извлечь что-либо полезное из данных?

Нельзя ли придумать другие данные, из которых можно было бы определить неизвестное?

Нельзя ли изменись неизвестное, или данные, или, если необходимо, и то и другое так, чтобы новое неизвестное и новые данные оказались ближе друг к другу?

Все ли данные вами использованы?

Все ли условия?

Приняты ли вами во внимание все существующие понятия, содержащиеся в задаче?

3. ОСУЩЕСТВЛЕНИЕ ПЛАНА.

Нужно осуществить план решения. Осуществляя план решения, контролируйте каждый свой шаг.

Ясно ли вам что предпринятый вами шаг правилен?

Сумеете ли вы доказать, что он осуществим?

4. ВЗГЛЯД НАЗАД (изучение полученного решения).

Нужно изучить найденное решение.

Нельзя ли проверить результат?

Нельзя ли проверить ход решения?

Нельзя ли получить тот же результат иначе?

Нельзя ли усмотреть его с одного взгляда?

Нельзя ли в какой-нибудь другой задаче использовать полученный результат или метод решения?