Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; з. Документ Microsoft Word (2). Система работы по формированию навыков решения текстовых задач. Лескевич Тамара Иосифовна, учитель математики Содержание
 Скачать 209.2 Kb. Скачать 209.2 Kb.
|
|
3. Этапы решения текстовой задачи Чтобы решить задачу, нужно определить её вид и тип. По отношению к теории существует два вида задач: стандартные и нестандартные. По типам задачи делятся: «на пропорциональность», «на сравнение величин», «на работу», «на части и проценты» и т. д. Весь процесс решения задачи можно разделить на восемь этапов: 1-й этап: анализ; 2-й этап: схематическая запись; 3-й этап: поиск способа решения; 4-й этап: осуществление решения: 5-й этап: проверка решения; 6-й этап: исследование задачи; 7-й этап: формулировка ответа; 8-й этап: анализ решения. Каким бы из основных методов не решалась текстовая задача /арифметическим, алгебраическим и геометрическим/, на 1 этапе анализа текста задачи необходимо выделить объекты, о которых идет речь в задаче, а также ее условие и вопрос, установить неизвестные и искомые величины, выделить ситуации, описанные в задаче. На 2 этапе поиска плана решения понадобятся умения записывать функциональную зависимость между величинами и выражать величины из формул, составлять из заданной задачи подзадачи, выделять из условия задачи предложения, выражающие зависимость между величинами, и преобразовывать их. На этапе реализации плана важнейшим оказывается умение переводить зависимости между величинами на математический язык. Перечислю эти умения. УМЕНИЕ СОСТАВЛЯТЬ КРАТКУЮ ЗАПИСЬ УСЛОВИЯ ЗАДАЧИ На этом этапе решения задачи происходит понимание или осмысление её текста. Намного облегчает этот процесс умение правильно “увязать” все известные и неизвестные величины в таблицу данных задачи или составить чертёж; неизвестные величины удобно обозначать знаком “?”, а “главный вопрос” задачи для того, чтобы потом на последних этапах не запутаться и правильно найти “Ответ”, так как в некоторых задачах, содержащих неявный вопрос искомую величину приходится довычислять; УМЕНИЕ ВЫПОЛНЯТЬ СХЕМАТИЧЕСКУЮ ЗАПИСЬ УСЛОВИЯ ЗАДАЧИ Особенно эффективно использую схемы при решении задач на движение. Обучение умению строить чертеж проводится по принципу от простого к сложному и реализуется по мере усложнения самих задач на протяжении всего курса математики. Вначале учащимся показывают образцы построения чертежей, потом предлагаются специальные упражнения на выбор чертежа, соответствующего условию задачи, на чтение чертежа. В конце концов, наступает черед заданий на составление задачи по чертежу, на построение чертежа по аналогии, на достраивание незаконченных или исправление чертежей. Проиллюстрирую сказанное. Задачи на движение ЗАДАЧА 1. Из двух городов, расстояние между которыми 650 км, вышли навстречу друг другу два поезда. Один шел со скоростью 50 км/ч, другой со скоростью 60 км\ч. Какое расстояние будет между поездами через 5 ч? 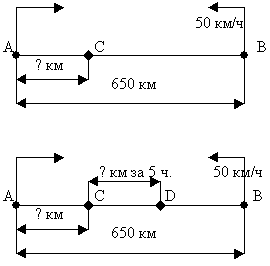 Из приведенных выше схем выберете ту, которая соответствует условию задачи. Объясните, что обозначают отрезки АВ, АС, ВD, CD на схеме? Составьте задачи по схемам. УМЕНИЕ ВЫБРАТЬ ВЕЛИЧИНУ, КОТОРУЮ БУДЕМ СЧИТАТЬ ПЕРЕМЕННОЙ Это умение формируется в средних классах на специальных упражнениях. Укажу одно из них. Сначала предлагается рассмотреть какую-либо задачу. ЗАДАЧА 2. Автобус проходит расстояние от города до села за 1, 5 ч, а легковая машина - за 0, 9 ч. Найти скорость автобуса, если известно, что она меньше скорости легковой машины на 40 кмlч. Задания: 1. Какую из неизвестных величин /скорость автобуса, скорость легковой машины или расстояние от города до села/ целесообразно считать переменной? 2. Какую величину было бы удобно обозначить через х , если бы скорость автобуса была больше скорости легковой машины? 3. Какую величину удобно обозначить через Х, если нужно найти расстояние от города до села? УМЕНИЕ АЛГЕБРАИЧЕСКИ ВЫРАЖАТЬ ВЕЛИЧИНЫ ЧЕРЕЗ ПЕРЕМЕННУЮ Это умение связано с предыдущим, так как от выбора переменной зависит составляемое по условию алгебраическое выражение. В начальной школе проводится пропедевтика этого действия: записывают числовые и буквенные выражения по условию задачи для его совершенствования в средних классах предлагаю упражнения на выражение неизвестных величин через выбранную переменную. Основным методом решения задач в 5-6 классы является арифметический. Использование арифметических способов решения задач развивает смекалку и сообразительность, умение ставить вопросы, отвечать на них, то есть развивает естественный язык, готовит школьников к дальнейшему обучению. Арифметические способы решения текстовых задач позволяют развивать умение анализировать задачные ситуации, строить план решения с учетом взаимосвязей между известными и неизвестными величинами (с учетом типа задачи), истолковывать результат каждого действия в рамках условия задачи, проверять правильность решения с помощью составления и решения обратной задачи, то есть формировать и развивать важные общеучебные умения. Арифметические способы решения текстовых задач приучают детей к первым абстракциям, позволяют воспитывать логическую культуру, могут способствовать созданию благоприятного эмоционального фона обучения, развитию у школьников эстетического чувства применительно к решению задачи (красивое решение!) и изучению математики, вызывая интерес сначала к процессу поиска решения задачи, а потом и к изучаемому предмету. Начиная с 7-го класса основным является алгебраический метод решения задач, для его использования, кроме общих, необходимы специальные умения. Но наряду с арифметическим способом решения задач уже в 5-м классе учу составлять уравнения по задачам. 4. Структура решения задач Структура задачи Задача Вопрос Условие Искомое Данные Связи Между искомыми Между данными Между искомыми и данными Структура решения задач умение анализировать текст задачи; поиск способа решения задачи; оформление найденного решения; работа над решенной задачей. Умение анализировать текст задачи умение читать текст задачи; умение выделять вопрос и условие; умение оформлять краткую запись; умение оформлять чертеж и рисунок по тексту задачи. Умение осуществлять поиск решения умение проводить вторичный анализ- это умение выделять искомые данные и устанавливать связи; умение переводить словесный текст задачи на математический язык; умение устанавливать полноту постановки задачи; умение актуализировать; умение проводить поиск плана решения задач. Умение оформлять найденное решение Умение завершить работу над задачей Умение осуществлять контроль решения задачи. Способы контроля: а) обратная задача; б) различные способы решения; в) прикидки на здравый смысл. Умение давать оценку результатам решения; Умение оценивать способ решения, делать выводы решения по способу решения; Умение составлять задачи. Приложение 1 Технология решения текстовой задачи на примере старинной задачи о кроликах и фазанах В клетке сидят фазаны и кролики. Всего в клетке 15 голов и 42 ноги. Сколько фазанов и сколько кроликов в клетке? Арифметический способ решения задачи Анализ текста задачи О чем говорится в задаче? Что сказано о количестве голов всех животных? А сколько голов у каждого животного? Сколько лапок у фазанов? А у кроликов? Что сказано в задаче о количестве лапок всех животных? Сформулируйте вопрос задачи. Краткая запись задачи Головы Лапки Фазаны ? 15 ? 42 Кролики ? ? Поиск решения задачи Какой главный вопрос задачи? Достаточно ли знать количество голов фазанов и кроликов, чтобы ответить на главный вопрос задачи? Какую полезную информацию можно почерпнуть зная, что каждое животное имеет одну голову и общее количество лапок равно 42? У кого лапок больше: у фазанов или кроликов и насколько? Найдется ли у каждого животного по две лапки? А сколько всего животных? Найдите сколько лапок будет у 15 животных, имеющих две лапки? О скольких лапках сказано в условии задачи? Есть ли "лишние"? Сколько? Кому принадлежат "лишние" лапки? Сколько не учтенных лапок у кроликов? Можно ли найти, сколько кроликов было в клетке? Как? Зная, сколько кроликов было в клетке, можем ли найти количество фазанов? Оформление решения задачи 15•2 = 30 (лапок) – у животных с двумя лапками. 42 – 30=12 (лапок) – "лишних". 12/2 = 6 (голов) – кроликов. 15 – 6 = 9 (голов) – фазанов. Проверка решения задачи 9•2 = 18 (лапок) – у фазанов. 6•4 = 24 (лапки) – у кроликов. 18 + 24 = 42 (лапки) – всего. Ответ: 6 кроликов, 9 фазанов. Решение задач на проценты Тема «Проценты» является универсальной в том смысле, что она связывает между собой многие точные и естественные науки, бытовые и производственные сферы жизни. Обучающиеся встречаются с процентами на уроках физики, химии, при чтении газет, просмотре телепередач. Умением грамотно и экономно проводить элементарные процентные вычисления обладают далеко не все обучающиеся. При решении задач проверяется не только владение определенным набором математических умений, но и умение анализировать ситуацию, рассуждать, делать выводы, проверять правильность полученного результата, применять знания в нестандартных ситуациях. Вся жизнь человека состоит из всевозможных испытаний. С различными контрольными работами, тестированиями, сочинениями и другими испытаниями мы встречаемся с первых дней обучения в школе. При подготовке к экзаменам повторение играет главную роль в формировании механизма воспроизведения материала на экзамене. А успешность воспроизведения материала во многом определяется способом его запоминания. Поэтому мы готовиться к выпускному экзамену за курс базовой школы заранее, начиная с 6-го класса. При подготовке учащихся к ЦТ я разобрала, систематизировала алгоритмы решения задач на проценты по способам их решения. В результате проделанной работы выделила три основные группы задач на проценты, с решениями которых предлагаю ознакомиться. Причины трудностей при понимании и решении задач на проценты: Первое знакомство учащихся с процентами происходит в 6 классе, решение задач на проценты изучается отдельно и не связывается с задачами на дроби; Проценты изучаются на первом этапе основной школы, в 5-6 классах, когда учащиеся в силу возрастных особенностей ещё не могут получить полноценные представления о процентах, об их роли в повседневной жизни. Далее в 6-ом классе изучение математических операций и приемов происходит отдельно, не переносятся на задачи на проценты; В решении задач на проценты применяют пропорции – тем самым процесс решения задач «механизируется», что мешает понимать смысл действий; В результате большинство учащихся задачи на проценты связывают только с пропорцией, а это относится лишь только к элементарным задачам; И еще одна проблема, которая делает проценты сложными для усвоения. Проценты от разных количеств нельзя сравнивать, складывать или вычитать. При правильном решении задач на проценты существенно то, от какого числа находят проценты. Подготовку к решению сложных задач на проценты следует начинать по следующей схеме: Схема последовательного изучения теории процента и подготовки к решению сложных задач на проценты: 1. Нахождение процента от числа. 2. Нахождение числа по его проценту. 3. Нахождение процентного отношения. 4. Сложные задачи на проценты. Понимание процентов и умение проводить процентные расчеты в настоящее время необходимо каждому человеку. Само определение процента позволяет легко решить простейшую задачу на проценты: найти заданное число процентов от заданной величины. Работа по решению задач на проценты проводится уже в 5 классе при изучении темы «Нахождение дроби от числа и числа по величине дроби» Подготовительный блок. Задачи на простые проценты Три основные задачи на проценты таковы: Найти процент от данного числа. Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь Данное число умножается на число процентов (проценты переводятся в десятичную дробь); 30% от 300 составляют 300∙0,3=90 Найти число по данной величине указанного его процента. Правило 2. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь. 3% вклада в сбербанк составляют 15000. Вклад в сбербанк составляет Нахождение процентного отношения чисел. Чтобы найти процентное отношение двух чисел а и b, надо отношение этих чисел умножить на 100 %, т.е. вычислить Пусть, например, при плановом задании 60 автомобилей в день завод выпустил 66 автомобилей, тогда он выполнил план на Приложение 2,3 При работе с одарёнными детьми при подготовке к олимпиаде использую более сложные задачи. Умение решать задачи такого вида необходимо и при подготовке к ЦТ Проценты при расчете зарплаты Задача 1. Подоходный налог в городе N установлен в размере 13%. До вычета подоходного налога 1% от заработной платы отчисляется в пенсионный фонд. Работнику начислено 50 000 р. Сколько он получит после указанных вычетов? Решение: За 100% приняты 50 000 р., начисленные работнику. 1) 50000/100=500 (руб.) – составляет 1%, который отчисляется в пенсионный фонд 2) 50000-500=49500 (руб.) – после отчисления в пенсионный фонд 3) За 100% - 49 500 руб. 49500/100=495 (руб.) – составляет 1% 4) 495∙13=6435 (руб.) - подоходный налог 5) 49500-6435=43065(руб.)- работник получит после указанных вычетов Ответ: 43065 руб. работник получит после указанных вычетов Задача 2. Какой будет заработная плата после повышения ее на 65%, если до повышения она составляла 10000 р.? Решение: 1) 10000/100=100 (р.) - составляет 1% 2) 100∙65=6500- повышение в рублях 3) 10000+6500=16500-зарплата после повышения Ответ: 16500 рублей. Задача 3. В городе N при внесении квартирной платы на один день позже установленного срока начисляется пеня в размере 0,1% от суммы платежа. Сколько придется заплатить в этом случае, если квартирная плата составила: 2600р; 800р? Решение: За 100% приняты 2600 руб. 2600/100=26 (руб.) – составляет 1% 26*0,1=2,6 (руб.) – составляет 0,1% 2600+2,6=2602,6 (руб.) - придется заплатить, если квартирная плата составила 2600р. За 100% приняты 800 руб. 800/100=8 (руб.) – составляет 1% 8*0,1=0,8 (руб.) – составляет 0,1% 800+0,8=800,8 (руб.) - придется заплатить, если квартирная плата составила 800р. |
