РЕФЕРАТ Особенности создания твердотельной геометрии корпуса суд. Системы геометрического моделирования
 Скачать 488.75 Kb. Скачать 488.75 Kb.
|
|
Введение Качество моделирования судовой поверхности – это одно из важнейших условий которое позволяет достичь снижения сроков, повышения качества сборки и сварки корпуса, что в конечном результате приводит к существенному снижению затрат на строительство. В конечном итоге затраты на исправление брака могут во много раз превысить затраты на моделирование. Идеальным является моделирование корпусных конструкций и листов обшивки без припусков, но при этом качество теоретической судовой поверхности должно быть безупречным. Для этой цели используются технологии автоматизированного проектирования (computer-aided design - CAD), автоматизированного производства (computer-aided manufacturing - САМ) и автоматизированной разработки и конструирования (computer-aided engineering - CAE). Все эти системы CAD/CAM/CAE вместе называются системами автоматизированного проектирования – САПР. Моделирование в САПР используются для решения многих задач. В системе разработчик изменяет форму модели, добавляет и удаляет ее части, детализирует форму визуальной модели. Трехмерная визуальная модель хранится в компьютере вместе со своим математическим описанием. Это позволяет решать задачи и выполнять операции, возникающие как в процессе разработки и производства продукта, так и на других этапах его жизненного цикла. В основе современных CAD-систем лежат технологии геометрического моделирования и параметрического проектирования. Системы геометрического моделирования. В CAD/CAM/CAE-системах всех уровней сложности геометрическое моделирование технических объектов, компьютерное решение геометрических и графических задач занимают центральное место. При создании реального объекта в первую очередь формируется геометрия этого объекта, его составных частей, после этого решаются другие задачи проектирования, технологии и изготовления. Проблемам геометрического моделирования, в том числе самому новейшему его направлению объемному твердотельному моделированию посвящено значительное число исследований. Подсистемы машинной графики и геометрического моделирования занимают центральное место в судостроительный и машиностроительный САПР. Конструирование изделий в них, как правило, проводится в интерактивном режиме при оперировании геометрическими моделями, т.е. математическими объектами, отображающими форму деталей, состав сборочных узлов и возможно, некоторыми дополнительными параметрами (масса, момент инерции, цвета поверхности и т.п.). Различают следующие системы геометрического моделирования: 1) каркасное моделирование (проволочное) 2) поверхностное моделирование (полигональное) 3) твердотельное моделирование (сплошное, объемное моделирование) Каркасное моделирование (wire frame modeling systems) - это исторически первая технология представления объемной геометрии. Она естественным образом развилась из систем 2D-черчения. Это самый простой способ представления трехмерных моделей - так называемые проволочные каркасы, или просто каркасы. В системах каркасного моделирования форма представляется в виде набора характеризующих ее линий и конечных точек. Линии и точки используются для представления трехмерных объектов на экране, а изменение формы осуществляется путем изменения положения и размеров отрезков и точек. Это моделирование самого низкого уровня. Имеет ряд серьезных ограничений, большинство из которых возникает из-за недостатка информации о гранях, заключенных между линиями и невозможности выделить внутреннюю и внешнюю область изображения твердого объемного тела. Однако каркасная модель требует меньше памяти и вполне пригодна для решения задач, относящихся к простым. Каркасное представление часто используется не при моделировании, а при отображении моделей как один из методов визуализации. 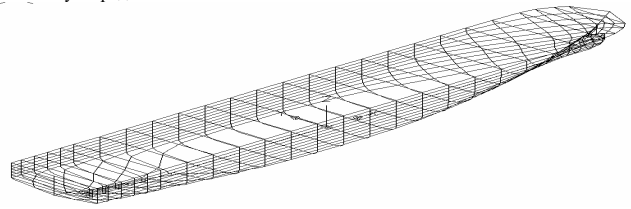 Рис.1 - Каркасная модель корпуса судна. Ограничения каркасной модели: 1) Неоднозначность. Нельзя отличить видимые грани от невидимых. Операцию по удалению невидимых линий можно выполнить только вручную с применением команд редактирования каждой отдельной линии, но результат этой работы равносилен разрушению всей созданной каркасной конструкции, т.к. линии невидимы в одном виде и видимы в другом. 2) Невозможность распознания криволинейных граней.Чтобы пытаться представить криволинейные грани, прибегают к ряду условностей (интерпретируя поверхность цилиндра плоскими гранями). Формируется условное изображение объекта. Наличие несущих линий может внести еще больше путаницы в чертеж, который и так уже полон неоднозначностей. 3) Невозможность обнаружить взаимное влияние компонентов.Каркасная модель не несет информации о поверхностях, ограничивающих форму, что обуславливает невозможность обнаружения нежелательных взаимодействий между гранями объекта и существенно ограничивает использование каркасной модели в пакетах, имитирующих траекторию движения инструмента при обработке объекта или создать сетку для конечно-элементного анализа, несмотря на то что объект кажется трехмерным. При таком моделировании не могут быть выявлены на стадии проектирования многие коллизии, появляющиеся при механической сборке. 4) Трудности при вычислении физических характеристик. 5) Отсутствие средств выполнения тоновых изображений. Основным принципом техники выполнения тоновых изображений, т.е. обеспечение плавных переходов различных цветов и нанесение светотени, является то, что затенению подвергаются грани, а не ребра. В настоящее время построение каркасов также используется в геометрическом моделировании САПР, но лишь как вспомогательная система промежуточных построений. Поверхностное моделирование (surface modeling systems) - В отличие от каркасного представления, моделирование при помощи поверхностей имеет существенно меньше ограничений, так как позволяет определить своеобразную «оболочку» трехмерного объекта.  Рис.2 – Поверхностная модель корпуса судна. Геометрические модели на основе поверхностного представления обеспечивают качественную визуализацию, более простой переход к построению расчетных сеток для численного моделирования, обеспечивают ряд полезных функций, таких как построение пространственных сопряжений, сечений, определения линии пересечения оболочек, генерацию чертежных проекций. Поверхностные модели различаются по способу аппроксимации поверхности. Более простой в части структуры данных и используемых для работы с ними алгоритмов является полигональная аппроксимация. Полигональная сетка (модель) представляет собой набор топологически связанных простых геометрических двумерных примитивов, которые описывают поверхность объекта. Этими примитивами являются полигоны, которые представляют собой фигуры с прямыми сторонами (3 и более сторон), определенными посредством точек трехмерного пространства (вершин) и соединяющих эти точки линий (ребер). Внутренняя область полигона называется гранью. Обычно в полигональной сетке вершины и ребра совместно используются разными гранями, так реализуется их топология. В этом случае их называют общими вершинами или общими гранями. Внешние ребра сетки называются граничными ребрами. 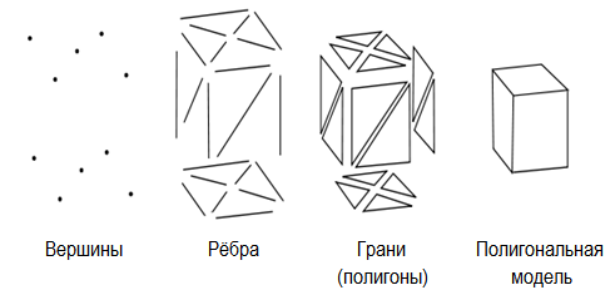 Рис.3 – Составляющие полигональной сетки. Главным ограничением подобной аппроксимации является то, что она имеет фиксированную точность, то есть отклонение положения модельной поверхности от «идеальной» моделируемой. Полигональная модель тем точнее и ближе к оригинальному объекту, чем меньше размер полигонов, и чем больше их количество. Это приводит к росту требований к вычислительным возможностям системы. Существует возможность повысить детализацию модели за счет увеличения количество полигонов в трёхмерной модели, используя кривые Безье. На этом основана технология NURBS (Non-UniformRational В-Spline, неоднородный В-сплайн), сегодня наиболее часто применяемая в практике САПР. Это особая технология, предназначенная для создания плавных органических форм и моделей, основанная на сложном математическом аппарате. Всего существует около 1500 уравнений для описания всех геометрических элементов, от простейших кривых до сложных поверхностей. Из-за особенности строения NURBS поверхности всегда гладкие (у них нет острых краев, присущих полигонам), поэтому они широко используются в органическом моделировании (подобном созданию растительных форм), для создания моделей животных, людей, машин и т. д. Любая NURBS-модель представляет собой некий набор NURBS-поверхностей, образованных NURBS-кривыми. Данные кривые описываются математическими формулами, в итоге отпадает необходимость запоминать каждую точку кривой, достаточно знать координаты ее начала и конца и математическую формулу, описывающую кривую. Это позволяет создавать сложные криволинейные поверхности с небольшим числом управляющих вершин и легко избавляться от грубой огранки объектов, придавая им плавную искривленную форму путем простого увеличения детализации.   Рис.4 – NURBS-поверхность Сфера. Самый простой вид NURBS-поверхностей — это NURBS-примитивы, представленные объектами Сфера (Sphere), Куб (Cube), Цилиндр (Cylinder), Конус (Cone), Плоскость (Plane) и Topус (Torus). Как и другие типы примитивов, NURBS-примитивы обычно используются в качестве основы для формирования более сложных моделей. Такое описание поверхности обеспечивает определение координат любой ее точки, радиуса кривизны в ней, направления нормали к поверхности с высокой заданной точностью. В определенной степени NURBS-представление является развитием полигонального, но в отличие от него позволяет описывать не только плоские, но и криволинейные грани и ребра. Совокупность таких граней с общими ребрами по традиции называют сеткой. Технология NURBS обеспечивает реализацию ряда функциональных возможностей, недоступных или существенно ограниченных при использовании каркасного либо полигонального представления: вычисление радиуса кривизны поверхностей, их гладкое сопряжение, построение траекторий на поверхности, что важно для подготовки ЧПУ программ, получение точных изображений, спроецированных на плоскость, например, для получения чертежных видов и т. д. и т. п. Полигональное моделирование, это моделирование только поверхности объекта, поэтому оно относится к пустотелому моделированию. Это проявляется в том, что при редактировании такой модели, если удалить часть полигонов, образуется дырка в поверхности, через которую будет видно всю внутреннюю часть модели. То есть такая модель в отличие от твердотельных моделей не имеет информации о своём объёме. Поэтому к недостаткам полигональных моделей можно отнести то, что из таких моделей невозможно получить сведения о физических свойствах объекта, таких как масса, объём, центр тяжести и др. Поверхностное моделирование играет важную роль при проектировании изделий из листового металла (sheet metal parts), таких как капоты и крылья автомобилей, где форма поверхности важна как для дизайна, так и для аэродинамики изделия. В отличие от авиационной или автомобильной промышленности, где форма корпуса разрабатывается и оптимизируется длительное время, сроки разработки поверхности в судостроении очень сжатые и в этом случае важное значение для построения судовой NURBS поверхности приобретает оптимальное разбиение поверхности на участки. При разбиении необходимо учитывать и ряд математических особенностей кривых и поверхностей. На основе длительного опыта NURBS моделирования судовой поверхности можно предложить следующие основные требования к разбиению поверхности на участки: - использование степени NURBS поверхностей не выше третьей. Более высокая степень дает дополнительную гладкость поверхности и вместе с тем увеличивает область изменения поверхности при коррекции одной контрольной точки. Тем самым теряется свойство локальности модификации поверхности и появляется необходимость увеличения количества контрольных точек. - обязательное выделение в отдельные участки поверхности поверхность между линиями сломов. Использование математических свойств NURBS для создания сломов внутри участка поверхности возможно, но трудоемко для управления и практически не поддерживается многими системами в случае необходимости передачи данных из одной системы в другую. - обязательное выделение участков плоского борта, плоского днища и участков линейчатых поверхностей позволяет эффективно управлять формой этих линий. Без выделения в отдельные участки поверхности получить корректную линию плоского борта или днища только посредством контрольных точек поверхности практически невозможно. - присущее NURBS ограничение на количество граничных линий участков поверхности (обычно три или четыре) можно обойти, используя обрезку поверхностей при этом моделирующая поверхность продляется за границы моделируемой области и обрезается по этим границам. - необходимо избегать разбиения гладких поверхностей на отдельные участки. Стыковка таких участков как правило производится только по первой производной и не дает необходимой гладкости. Сечения поверхности в этом районе не будут выглядеть достаточно гладкими даже визуально. Только в случае радиального сопряжения поверхностей стыковка допустима и выглядит вполне естественно – в этом случае нет необходимости выдерживать условие непрерывности вторых производных. - сложностей с моделированием формы углов участков поверхностей можно избежать только путем изменения формы граничных линий участка поверхности. Контрольные точки внутри поверхности практически не могут повлиять на углы входа сечений поверхности в окрестности угловой точки. Следование вышеперечисленным требованиям позволяет избежать большого количества проблем при моделировании, сократить время и повысить качество поверхности. Твердотельное (объемное) моделирование (solid modeling systems)- логическое развитие каркасного и поверхностного моделирования. Твердотельное моделирование является самым совершенным и самым достоверным методом создания копии реального объекта. В основу модели положен принцип формирования сложной модели из элементарных объёмов (базисных тел - параллелепипеда, куба, сферы, цилиндра, конуса, клина, тора) а также, как результат вращения, выдавливания областей с использованием логических операций объединения, вычитания, пересечения (булевы операции). Одно из достоинств тел (твердотельных объектов) заключается в том, что их можно анализировать: можно вычислить такие свойства тел, как масса, центр тяжести, площадь поверхности. Имеют внутренность и объём. 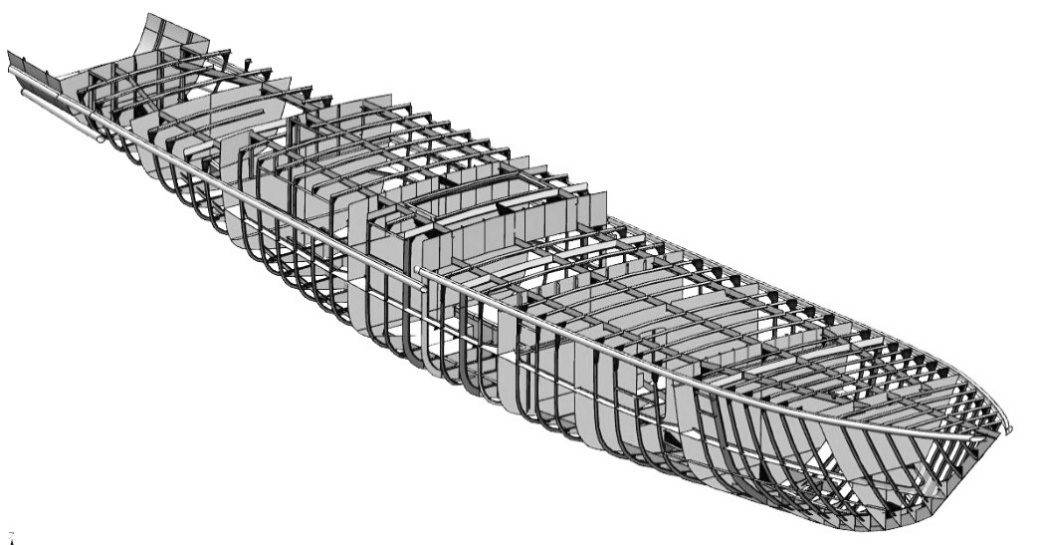 Рис.5 – Объемная модель корпуса судна. Твердотельная модель строится путем создания целостной, не имеющей разрывов совокупности поверхностей, которые сшиты между собой и образуют правильный замкнутый геометрический объем, то есть твердое тело содержит внутренний объем, ограниченный внешней поверхностью. Изменение одной из них приводит к изменению других. Фундаментальным свойством твердотельного моделирования является сохранение топологии элементов тела (отношения элементов - их взаимного расположения). Сохранение связей элементов тела обеспечивает замкнутость и непротиворечивость объема твердого тела. Установленные между элементами связи сохраняются вместе с геометрической информацией в базе данных. Методы твердотельного моделирования, основанные на булевых операциях, особенно удобны при вычислении поверхностных и весовых характеристик тел, расчете напряжений, имитации операций механической обработки. В последнем случае операции резания металла (точение, фрезерование, сверление и т. п.) могут быть легко описаны при помощи булевой разности. Методы создания твердотельных моделей подразделяются на два класса: 1. Метод конструктивного представления (C-Rep) Метод конструктивного представления заключается в построении сложных твердотельных моделей, из базовых простейших составляющих элементов, называемых твердотельными примитивами, которые определяются формой, размером, точкой привязки и ориентацией. Каждый примитив определен некоторой формой (параллелепипед, цилиндр переменного сечения, шар, куб, сфера, конус, клин и т.п.), точкой привязки, исходной ориентацией и изменяемыми размерами. Построение базовых примитивов заключается в создании тел с помощью развертки (выдавливания, вращения и перемещения вдоль кривой) двухмерных областей в трехмерном пространстве. При этом образуется объем (замкнутое пространство, определяемое параметрами эскиза и выдавливания вдоль кривой) – твердое тело. Редактирование таких моделей сводится к изменению параметров эскиза и выдавливания, после чего перестраивается модель тела. 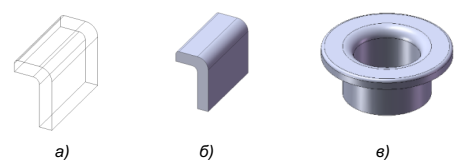 Рис.6 – Перемещение поверхности: а – исходное сечение и каркасная модель; б – твердотельная модель в результате выдавливания; в – результат вращения. Главным инструментарием для построения модели С-Rep являются булевы операции. Чаще всего используются операции: - Операция объединения определяет пространство внутри внешней границы составной формы, полученной из двух тел с общей областью. - Операция разности определяет пространство, ограниченное поверхностью, оставшейся от одной формы, и внешней границей общей области двух форм. Например, модель корпуса судна с отверстием для подруливающего устройства в ней может быть получена вычитанием цилиндра из модели корпуса. - Операция пересечения определяет пространство внутри границ общей области объектов. 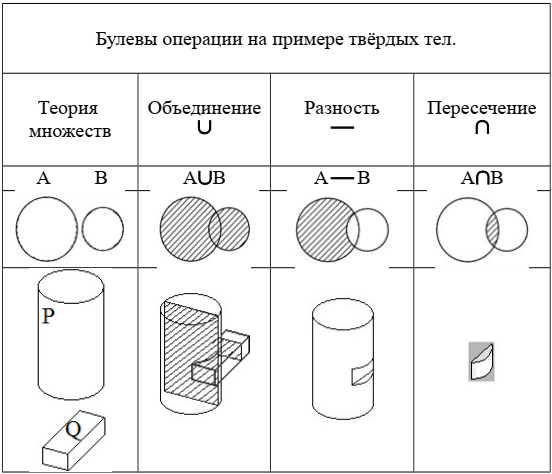 Рис.7 - Булевы операции на примере твёрдых тел. 2. Метод граничного представления (поверхностный) (B-Rep) Метод граничного представления (B-Rep) также оперирует с примитивами, связанными при помощи булевых операций. Граничное представление – задание граничных элементов детали – параметрически описанных поверхностей (граней - face), ребер (границы или же пересечения граней), вершин (часть/точка на кривой, формирующей ребро), описывающих тело. Эти данные дополняются информацией о топологии примитива и особенностях его геометрии. В этом методе задаётся ось и контур будущего объекта, далее происходит построение области, занятой контуром. Затем удаляют скрытые линии и закрашивают поверхности с учетом их свойств. Именно ребра и грани образуют трёхмерную граничную поверхность объёмного тела. Это единственный метод, позволяющий создать точное, а не приближенное представление геометрического твердого тела. При таком подходе от пользователя требуется задание контуров или границ объекта, а также эскизов поверхностей разных видов, и указание линий связей между этими поверхностями, чтобы можно было установить взаимное соответствие. B-Rep метод актуален в образовании сложных структур, которые очень сложно воссоздать при помощи C-Rep метода. Так же преимуществом систем с B-Rep является простейшее изменение граничного представления в данную каркасную модель и обратным ее изменением. Причиной тому является то, что описание границ аналогично описанию каркасной модели. 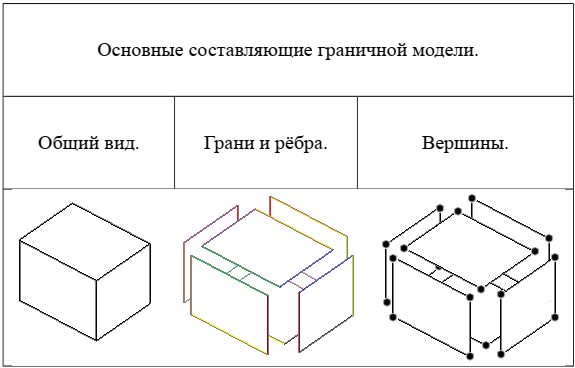 Рис.7 - Основные составляющие граничной модели. Достоинства и недостатки методов C-Rep и B-Rep: - система с C-Rep представлением имеет преимущества при первоначальном формировании модели, так как построить объемную модель правильной формы из объемных примитивов с использованием булевых операций достаточно просто. Кроме того, этот метод обеспечивает более компактное описание модели в БД; - B-Rep представление является актуальным при создании сложных форм, которые воссоздать с помощью C-Rep метода очень трудоемко; - в C-Rep методе модель хранится в виде комбинации данных и логических процедур, при этом требуется меньше памяти, но большим оказывается объем вычислений при воспроизведении модели. С другой стороны, модели c B-Rep представлением хранит точное описание границ модели, для этого нужно больше памяти, мощные аппаратные средства и ПО, но не требуется почти никаких вычислений для воссоздания изображения; - относительным достоинством систем с B-Rep является сравнительная простота преобразования граничного представления в соответствующую каркасную модель и обратно. Причина такой простоты заключается в том, что описание границ подобно описанию каркасной модели, а это облегчает преобразование модели из одной формы в другую, и делает системы с B-Rep представлением совместимыми с уже имеющимися системами. К методам машинной графики относят методы преобразования графических объектов, представления (развертки) линий в растровой форме, выделения окна, удаления скрытых линий, проецирования, закраски изображений. Преобразования графических моделей выполняются с помощью операций переноса, масштабирования, поворота. Для геометрического ядра современных CAD/CAM/CAE-систем характерна интеграция методов твердотельного моделирования трехмерных объектов и традиционных методов математического моделирования сложных криволинейных поверхностей. Мировыми лидерами в области программного обеспечения САПР для судостроения и машиностроения считаются FORAN, TRIBON, Pro/Engineer, Unigraphics, EUCLID, CADDS5, CATIA, I-DEAS и ряд других. Отметим, что по своим функциональным возможностям эти комплексы приблизительно равноценны, новые достижения, появившиеся в одном из них, в скором времени реализуются в новых версиях других комплексов. Заключение Форма технического объекта в первую очередь обусловлена его функциональным назначением, кроме этого в ряде случаев она должна удовлетворять и эстетическим требованиям, обеспечивать хорошие гидроаэродинамические характеристики. В судостроении при моделировании обводов судна, гребного винта критерием оценки совершенства модели являются гидродинамические характеристики, а для пассажирских судов и яхт эстетические характеристики. Основными требованиями, предъявляемые к методам конструирования криволинейных обводов для обеспечения интеграции с методами твердотельного моделирования являются: Получение заданной формы геометрического объекта с использованием минимального количества параметров. При этом предполагается, что часть из них является обязательными, а другие параметры влияют на точность описания. Желательно, чтобы конструктор имел возможность задавать эти параметры в графическом виде. Выбираемый класс кривых или поверхностей должен описываться достаточно просто (лучше в параметрическом виде). Кривые и поверхности выбранного класса должны быть гладкими (быть непрерывными вместе с производными на заданном интервале), т.е. не рваться, иметь непрерывно изменяющуюся касательную, непрерывные кривизну и кручение (для пространственных обводов), что обеспечивает гладкую стыковку участков обвода. В методах должны использоваться "несложные" алгоритмы глобальной и локальной модификации формы обводов. Как для одномерных, так и для двумерных обводов локальная модификация должна допускать изменение формы участка или всего обвода в целом. При этом необходимо использовать алгоритмы вычисления небольшого количества контрольных точек, определяющих форму обвода. Обеспечение качества аппроксимации. Сконструированные криволинейные обводы должны "вести себя" предсказуемо для достаточно больших массивов точек; Отклонения не должны превышать заданных значений; Особые точки должны легко определяться; Используемые при описании обводов функции должны допускать операцию многократного дифференцирования. Возможность построения аналитически простых кривых и поверхностей (в частности, прямых линий и плоскостей), а также возможность решения позиционных и метрических задач с помощью устойчивых вычислительных процедур. Аффинные преобразования включают в себя вращение, растяжение, сжатие, параллельный перенос и их возможные комбинации. К проективным преобразованиям относят также построение перспективы. К снижению вычислительных затрат ведет следующая последовательность операций. Сначала преобразуется какой-либо набор параметров, определяющих форму обвода (например, массив управляющих точек Безье), затем производится вычисление точек (построение) самого обвода. Для обеспечения возможности применения аффинных и проективных преобразований сконструированные криволинейные обводы должны обладать свойством аффинной и проективной инвариантности. Возможность применения стандартных методов визуализации. Перечисленным требованиям в большей степени удовлетворяют параметрические полиномиальные функции и рациональные параметрические функции. Обобщение методов Безье и B-сплайнов позволило получить одно из мощнейших и универсальных средств геометрического моделирования криволинейных обводов NURBS-технологию. Литература Алексанов А. Правила и требования моделирования судовых поверхностей на основе многолетнего опыта использования системы Sea Solution URL: http://www.shipcad.ru/article/article13.php. Князьков В. В. Технологии CAD-систем в инженерном графическом образовании // Научно-методический электронный журнал «Концепт». – 2012. – №4 (Апрель). – С. 46–50. – URL: http://e-koncept.ru/2012/1242.htm. Корж Р.С. Автоматизация построения 3D моделей по результатам лазерного сканирования — URL: https://nauchkor.ru/uploads/documents/587d36385f1be77c40d589ba.pdf Кузнецов А., Рябоконь А., Платонов Ю. Проектирование корпуса судна и комплекс автоматизации раскроя на платформе Autodesk // Журнал «САПР и Графика». – 2012. – №6 (Июнь). – С. 66–71. – URL: http://esg.spb.ru/files/articles/106/nXj1PeK2ni.pdf Лапшин И.А. Применение информационных технологий в технической подготовке производства судов — URL: https://sapr.ru/article/20941 Плоткин Э., Рябоконь А., Платонов Ю. Решения для судостроения на платформе AUTODESK (SHIPCONSTRUCTOR, SHIPMODEL) // Информационно-аналитический журнал «Rational Enterprise Management». – 2010. - №3(Март). –С. 66-71. – URL: http://esg.spb.ru/files/articles/27/oOD8TgIA5V.pdf Поляков Ю. Н. Комплексы программ для создания 3D геометрических моделей судов на ранних стадиях проектирования // Научно-технический и производственный журнал «Судостроение». – 2015. – №6 (Ноябрь-Декабрь). – С. 9–12. – URL: http://www.sstc.spb.ru/upload/iblock/e2a/2015_6.pdf Цуренко Ю.И. Автоматизированное построение теоретической поверхности корпуса судна. Электронное учебное пособие для студентов специальности 140100 – «Кораблестроение». Северодвинск, СЕВМАШВТУЗ, 2006 – 180 с., ил. — URL: https://narfu.ru/university/library/books/1755.pdf Цуренко Ю.И. Введение в автоматизацию проектирования корабля. Конспект лекций — URL: https://narfu.ru/university/library/books/1756.pdf Чемпинский Л.А. Основы геометрического моделирования в машиностроении: конспект лекций - Самара: Изд-во Самарского университета, 2017. - 160 с. — URL: http://repo.ssau.ru/bitstream/Metodicheskie-materialy/Osnovy-geometricheskogo-modelirovaniya-v-mashinostroenii-Elektronnyi-resurs-kurs-lekcii-71532/1/Чемпинский%20Л.А.%20Основы%20геом.%20моделир.%20Курс%20лекций%202017.pdf Интернет-ресурс «САПР в судостроении» URL: http://www.shipcad.ru Интернет-ресурс «T-FLEX CAD» URL: https://www.tflexcad.ru |
