Моделирование процессов и объектов. Системная динамика
 Скачать 285.19 Kb. Скачать 285.19 Kb.
|
|
РГР по дисциплине: «Моделирование процессов и объектов» тема: Системная динамика
Основные понятияПодход, называемый системной динамикой, соответствует высокому уровню абстракции. В соответствии с этим подходом, предложенным в 1950-х гг. американским ученым Джеем Форрестером, структура и поведение моделируемой системы представляются как множество взаимодействующих положительных и отрицательных обратных связей и задержек. Методология системной динамики была построена так, чтобы сделать применимой на практике философию развития. Для этого были использованы и модифицированы известные методы представления потоковых диаграмм. Функционирование системы описывается в терминах накопителей, потоков между этими накопителями и информации, определяющей количественные характеристики этих потоков. Другими словами, системно-динамические модели состоят из петель обратной связи, которые формируют поведение системы. Системная динамика позволяет моделировать сложные системы на высоком уровне абстракции, не принимая в расчет мелкие детали: индивидуальные свойства отдельных продуктов, событий или людей. Такие модели позволяют получить общее представление о системе и хорошо подходят для стратегического планирования. Например, когда мобильный оператор разрабатывает свою маркетинговую кампанию, он может смоделировать её и проанализировать эффективность новых способов коммуникации с клиентами, не моделируя поведение каждого клиента в отдельности. Причинно-следственные диаграммы позволят описать глобальное поведение системы. Сложные взаимосвязи встречаются повсеместно, в любых сферах бизнеса и исследований. Системная динамика помогает разобраться в них, отследить результаты внесения изменений в систему, протестировать разные варианты и оценить их эффективность. Особенности методаОсновными характеристиками сложных систем являются следующие факторы: Динамичность или склонность к временным изменениям; Петли обратной связи; Задержки; Нелинейность и так далее. С помощью метода можно успешно ставить опыты с системами на стадии проектирования, а не на практике, что облегчает возможное решение задач в дальнейшем. Подобные модели, служат оптимальным средством для исследования характера поведения системы в определенных искусственно созданных условиях, которые выбирает исследователь. Отсюда вытекает ряд важных плюсов в применении описываемого метода, который решает: Трудные ситуации, из которых невозможно выйти любым иным способом; Проектирование и имитация действия систем в неизвестных ранее случаях, чаще всего помогает эффективно решить поставленную задачу; Позволяет моделировать предполагаемую обстановку во время обстоятельств, требующих длительного времени, либо в тех случаях, когда требуется ускорить или замедлить ход действий во время имитации будущего процесса. Во всех вышеперечисленных случаях метод значительно упрощает работу, прогнозирование и решение текущих задач без перенесения ситуаций в режим реального времени. Еще одна важная особенность — с помощью системной динамики маркетологи выстраивают модели абстрактных систем, без учета деталей. Это может быть рассмотрение специфических особенностей продукта и т.п. При наличии подобной модели у специалистов складывается общее понятие о системе, что удобно использовать при формировании бизнес-стратегий. Например, когда фирма планирует запустить рекламную кампанию, сотрудники могут построить ее идеальную модель и произвести анализ эффективности обратной связи и взаимодействия с потребителями. При этом не моделируя поведение каждого отдельного покупатель; в бизнесе мотивация сотрудников влияет на производительность, качество рекламы — на восприятие бренда. Всегда есть причина и следствие, а также часто есть временная задержка: результаты ваших нововведений проявляются далеко не сразу, их эффективность можно оценить только после долгого наблюдения за системой. Компьютерные модели способны решить эту проблему. Взаимозависимости, такие как качество рекламы и восприятие бренда, в модели обычно представляются в виде циклов, которые называют циклами обратной связи. Например, чем больше денег вы вкладываете в маркетинг, тем больше ваши доходы, и тем больше денег вы можете потратить на маркетинг. Циклы обратной связи — базовая концепция системной динамики. Системная динамика позволяет оперативно ориентироваться во взаимосвязях в любых областях бизнеса, отслеживая результаты изменений в системе, проводя тестирование различных способов и исследуя их возможную продуктивность. Плюсы и минусыОдним из положительных аспектов имитационного построения модели является диалог экспериментатора с набором средств, реализующим данную схему. При этом аналитику весьма удобно использовать весь свой имеющийся опыт и знания, что позволяет лучше контролировать результаты процесса и корректировать движение проектируемой ситуации. Это нужно для того чтобы приобрести новые сведения о характере процессов наблюдения, а также может помочь в дальнейшем обучении специалистов работе с новыми сложными системами. Но есть и свои минусы: ограничение точности моделирования. Помимо этого создание такой модели требует существенных временных и прочих затрат, и обходится подчас дороже аналогичных методов. Пожалуй, это один из главных недостатков, но, несмотря на это, системно-динамическое моделирование пользуется широким спросом для решения синтетических задач и изучения сложных систем. Оно считается весьма эффективным и популярным методом прогнозирования и проектирования. Рассматриваемая модель наиболее продуктивно используется при решении следующих проблем: Изучения и анализа сложных систем для установления причин, следствий и их взаимосвязей; Составления прогноза результатов любых плановых изменений, используемых в управлении сложных систем; Обучения специалистов взаимодействию со сложными природными и техническими объектами и т.д. Циклы обратной связиОписать циклы обратной связи и смоделировать реальный мир в системной динамике можно с помощью накопителей (материалы, знания, люди, деньги), потоков между накопителями и динамических переменных — меняющихся во времени элементов данных. Системная динамика не принимает в расчёт единичные события и даёт общее представление о системе, фокусируясь на глобальных трендах. Системно-динамический метод позволяет: Создавать абстрактные модели без лишних деталей. Использовать глобальные взаимосвязи и задавать значения параметров и переменных в системе. В реальном мире зависимости никогда не бывают линейными, поэтому для их моделирования нужны более мощные инструменты, чем таблицы. С точки зрения математики, системно-динамическая модель представляет собой систему дифференциальных уравнений, которые решаются численно, когда модель запущена. МодельДля описания развития сетевой эпидемии используется SIR-модель. В модели хосты существуют в трех состояниях: уязвимом (S — susceptible), зараженном (I — infectious) и невосприимчивом (R — removed). SIR-модель развития эпидемии инициализируется с параметрами, представленными в таблице 1. Графическое представление модели и связей в ней показано на рисунке 1. Таблица 1 — Исходные данные SIR-модели
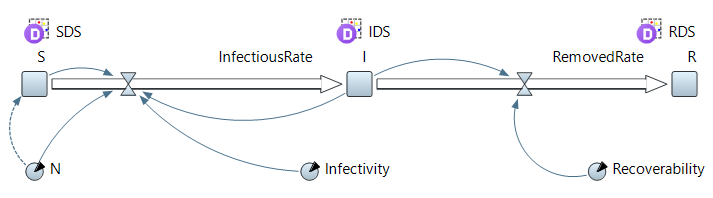 Рисунок 1 — SIR-модель развития эпидемии Проводится экспериментальное исследование SIR-модели с заданными параметрами с целью изучения динамики распространения сетевого вируса (рисунок 2). 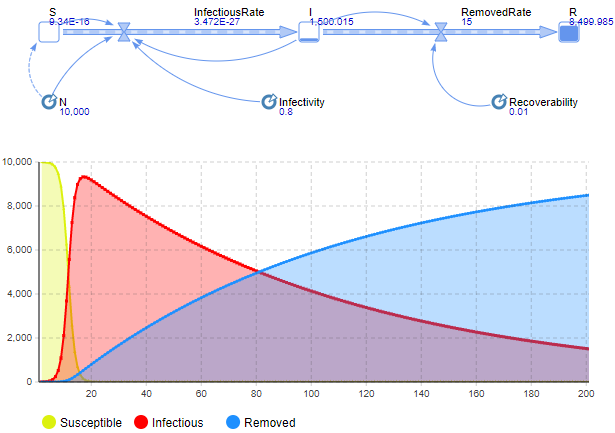 Рисунок 2 — Проведение эксперимента для SIR-модели развития эпидемии и график динамики распространения сетевого вируса Пик развития эпидемии (заражено максимальное количество хостов) достигается в момент времени, равный 17 единицам модельного времени. Пиковое значение «зараженных» хостов равно 9324. Процесс развития эпидемии завершается в момент, когда все хосты приобрели «иммунитет» к моменту времени, равному 1162 единицы модельного времени (9999,9 хостов с «иммунитетом»). Это же экспериментальное исследование SIR-модели можно провести, запустив эксперимент с варьированием параметров. В данном случае распространение сетевого вируса изучается с варьированием параметра Infectivity для каждого из состояний модели. Начальное значение равно 0.5, для эксперимента шаг варьирования равен 0,08. Результаты разных прогонов модели представлены на рисунке 3. 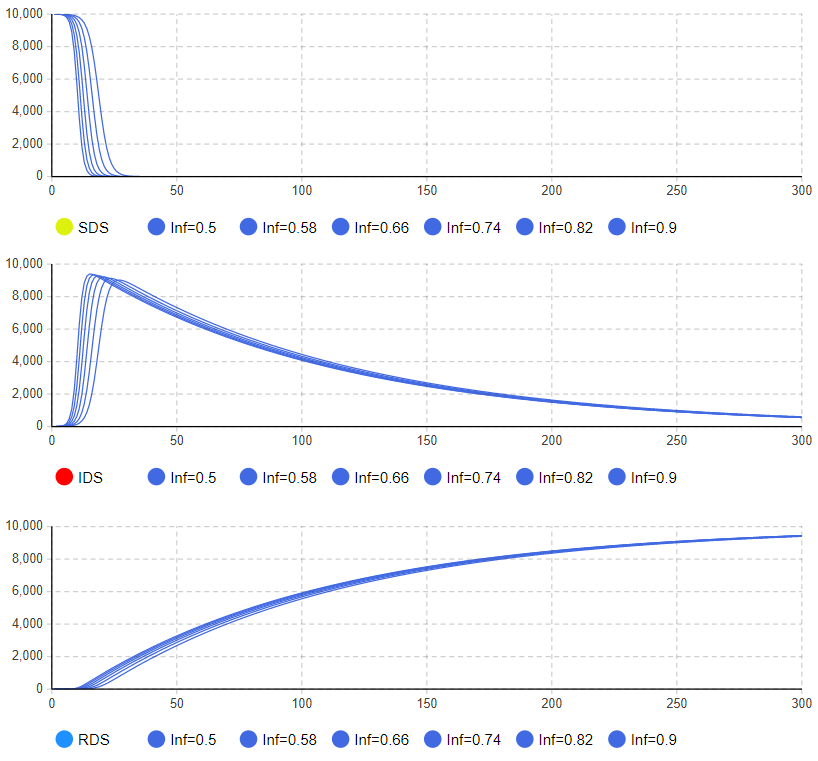 Рисунок 3 — Экспериментальные исследования SIR-модели распространения сетевого вируса с варьированием параметра Infectivity для каждого из состояний модели Как видно из ряда проведённых экспериментов, при увеличении параметра Infectivity, пик инфицированных и тенденция протекания эпидемии значительно не изменяются, зато максимальное количество хостов заражается за меньшее время. Но при всём этом, с увеличением параметра Infectivity быстрее происходит излечивание «зараженных» хостов. На количество «невосприимчивых» хостов варьирование параметра существенным образом не влияет. Модификация моделиДля описания развития сетевой эпидемии также может использоваться SAIR-модель, которая предусматривает использование на хостах сети антивирусного программного обеспечения за счёт введения нового антивирусного состояния (A — antidotal). SAIR-модель развития эпидемии инициализируется с параметрами, представленными в таблице 2. Вводятся следующие параметры: 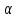 — скорость установки антивирусного программного обеспечения; — скорость установки антивирусного программного обеспечения; 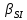 — частота заражения уязвимых хостов; — частота заражения уязвимых хостов; 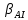 — частота заражения новым червем хостов с установленным антивирусом; — частота заражения новым червем хостов с установленным антивирусом; 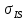 — частота восстановления зараженных хостов; — частота восстановления зараженных хостов; 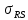 — частота восстановления удаленных хостов при вмешательстве оператора; — частота восстановления удаленных хостов при вмешательстве оператора; 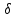 — частота удаления зараженных хостов. Графическое представление модели и связей в ней показано на рисунке 4. — частота удаления зараженных хостов. Графическое представление модели и связей в ней показано на рисунке 4.Таблица 2 — Исходные данные SAIR-модели
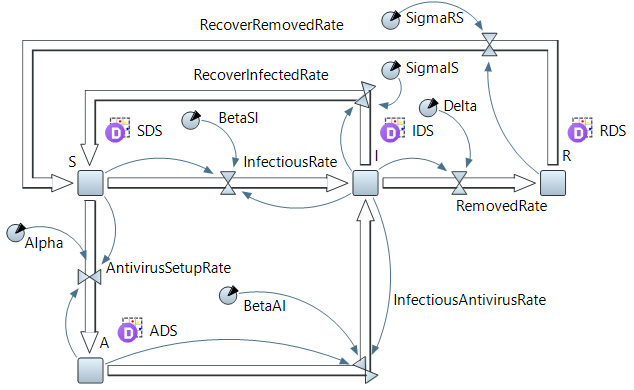 Рисунок 4 — SAIR-модель развития эпидемии Проводится экспериментальное исследование SAIR-модели с заданными параметрами с целью изучения динамики распространения сетевого вируса (рисунок 5). 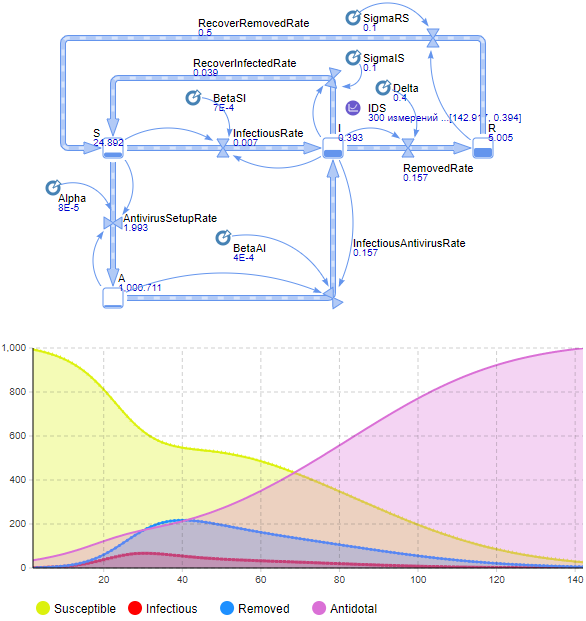 Рисунок 5 — Проведение эксперимента для SAIR-модели развития эпидемии и график динамики распространения сетевого вируса Пиковое значение инфицированных хостов наблюдается в момент времени, равный 31 единицы модельного времени. Пиковое значение равно 67. В течение периода наблюдения заметна обратная пропорциональная зависимость между уязвимыми хостами и хостами с антивирусом: число первых линейно уменьшается с ростом числа вторых соответственно. ВыводыМоделирование систем – мощный инструмент для их мониторинга, прогнозирования и планирования. Один из способов предсказания поведения системы – это сбор исторических данных и моделирование в течение требуемого времени. Такой вид предсказания часто работает, когда имеем дело с системами, которые повторяют свое поведение с некоторой периодичностью. Помимо статистических методов, существуют и другие подходы к получению разумных прогнозов. В течение долгого времени различные виды моделирования и математические модели использовались для того, чтобы понять, как ведут себя сложные системы и какие способы их улучшения существуют – например, это может быть метод непрерывного моделирования. В настоящее время многие системы подключены к Интернету, например, в парадигме IoT, когда огромное количество устройств, большинство из которых были хорошо известны и работали в автономном режиме, подключились к Интернету. С одной стороны, такой сдвиг дает возможность собирать больше информации о фактическом поведении системы, что может улучшить управляемые, оптимизированные и эффективные системы. Но, с другой, большими объемами данных сложно управлять. Чтобы получить большую ценность из собранных данных, важно преобразовать необработанные данные в информацию, что поможет принимать правильные решения. Что касается данных, то трудно принять какое-либо существенное решение, пока эти данные «сырые». Новосибирск 2022 |
