|
|
статистика экзамен. Слово статистика от лат
Размах вариации (R)
Размах вариации — это разность между максимальным и минимальным значениями признака
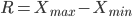
Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Пример
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность 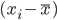 . .
При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю 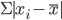 , либо возводить значения отклонений в квадрат , либо возводить значения отклонений в квадрат 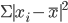
Среднее линейное и квадратическое отклонение
Среднее линейное отклонение 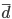 — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней. — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
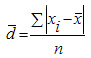
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
В нашем примере: 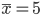 лет; лет;
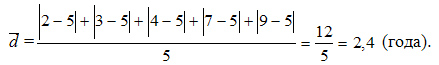
Ответ: 2,4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
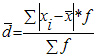
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение (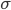 ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической: ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
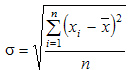
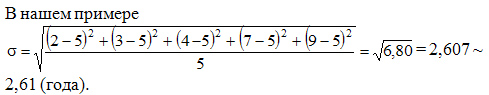
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
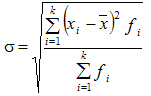
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: 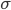
1,25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
23. Ряды динамики
Одной из важнейших задач статистики является практическая помощь ее в работе менеджера. Ряды динамики позволяют изучить данный показатели или целую их систему в процессе, в движении, что значительно расширяет аналитические возможности работы людей разных профессий.
Ряды динамики представляют собой ряды изменяющихся во времени значений статистического показателя, расположенного в хронологическом порядке.
Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени. [3]
Любой ряд динамики состоит из двух элементов:
1. показатель времени ti - это моменты или периоды времени, к которым относятся числовые значения показателей;
2. уровень ряда yi , под которым понимается значение статистического показателя, относящееся к определенному моменту или периоду времени.
Каждый ряд динамики может быть представлен в табличной форме - в виде пар значений ti и yi; и в графической форме - в виде линейной диаграммы.[4]
Классификация рядов динамики производится по следующим признакам.
1. В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
2. В зависимости от того, как выражаются уровни ряда на определенные моменты времени (на начало месяца, квартала, года и т. п.) или его величину на определенные интервалы времени (например за сутки, месяц, год и. т. п.), различают соответственно моментные и интервальные ряды динамики.[3]
При обработке статистических данных используются ряды динамики, различающиеся по следующим признакам:
1) по времени,
2) по форме представления уровней,
3) по числу показателей,
4) по расстоянию между датами или интервалами.[4]
5) в зависимости от наличия основной тенденции[3]
1) По времени различают моментные и интервальные ряды динамики.
- В моментных рядах уровни выражают состояние явления на критический момент времени - начало месяца, квартала, года и т.д.
Например, численность населения, численность работающих и т.д. В таких рядах каждый последующий уровень полностью или частично содержит значение предыдущего уровня, поэтому суммировать уровни нельзя, так как это приводит к повторному счету[4]. Особенность моментного ряда состоит в том, что его уровни, как правило, содержат элементы повторного счета, например число вкладов населения, учитываемых за январь, существует и в настоящее время, являясь единицами совокупности в июне. В результате чего суммировать уровни ряда не целесообразно.[3]
- В интервальных - уровни отражают состояние явления за определенный период времени - сутки, месяц, год и т.д. Это ряды показателей объема производства, объема продаж по месяцам года, количества отработанных человеко-дней и т.д.[4] Особенность интервального ряда состоит в том, что его уровни характеризуют собой суммарный итог какого либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени, их можно суммировать, как не содержащие повторного счета.[3]
2) По форме представления уровней различают ряды абсолютных, относительных и средних величин.
3) По числу показателей выделяют изолированные и комплексные ряды динамики (многомерные).
Изолированный ряд строится по отдельному показателю, комплексный - по системе взаимосвязанных показателей.
4) По расстоянию между датами или интервалами ряды динамики делятся на ряды с равноотстоящими и неравноотстоящими уровнями.
В рядах с равноотстоящими уровнями расстояние между датами или периодами одинаково, в рядах с равноотстоящими уровнями - оно различно.
5) В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные.
Если математическое ожидание значения признака и дисперсия постоянны, не зависят от времени, процесс считается стационарным и ряды динамики также называются стационарными. Экономические и социальные процессы во времени обычно не являются стационарными, так как содержат основную тенденцию развития, но их можно преобразовать в стационарные путем исключения тенденций.[3]
Аналитические показатели изменения уровней ряда динамики
К индивидуальным показателям интенсивности изменения явления относятся:
- абсолютный прирост Дyi ;
- темп роста Ti (коэффициент роста Ki );
- темп прироста Ti' (коэффициент прироста Ki' );
- абсолютное значение одного процента прироста Ai
24. Основные показатели динамики
Простейшими показателями анализа, которые используются в первую очередь при измерении скорости изменения уровня ряда динамики, являются абсолютный прирост, темпы роста и прироста, а также абсолютное значение одного процента прироста. Расчет этих показателей основан на сравнении между собой уровней ряда динамики. При этом уровень, с которым производится сравнение, называется базисным, т.к. он является базой сравнения. Обычно за базу сравнения принимается либо предыдущий, либо какой-либо предшествующий уровень, например первый уровень ряда.
Если каждый уровень сравнивается с предшествующим, то полученные при этом показатели называются цепными, т.к. они представляют собой как бы звенья «цепи», связывающие уровни ряда. Если же все уровни сравниваются с одним и тем же уровнем, выступающим как постоянная база сравнения, то полученные при этом показатели называются базисными.
Абсолютный прирост на базисной основе вычисляется по формуле:
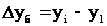 , (1.2.1.1а) , (1.2.1.1а)
где: Dуб – абсолютный прирост;
yi – сравниваемый уровень;
y1 – начальный уровень.
Абсолютный прирост на цепной основе рассчитывается как:
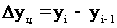 , (1.2.1.1б) , (1.2.1.1б)
где: Dуц – абсолютный прирост;
yi – сравниваемый уровень;
yi-1 – предыдущий уровень.
Темп роста показывает во сколько раз увеличился уровень по сравнению с базисным, а случае уменьшения – какую часть базисного уровня составляет сравниваемый уровень.
Базисный темп роста:
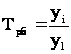 . (1.2.1.2а) . (1.2.1.2а)
Цепной темп роста:
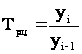 . (1.2.1.2б) . (1.2.1.2б)
Темп прироста характеризует относительную величину прироста, т.е. его величину по отношению к базисному уровню:
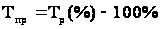 . (1.2.1.3) . (1.2.1.3)
Абсолютное значение (содержание) одного процента прироста вычисляется по формуле:
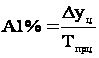 . .
27. В настоящее время, по оценкам ученых, насчитывается свыше 150 различных методов прогнозирования. Однако на практике используется в качестве основных 15-20. В существующих источниках представлены различные классификационные принципы методов прогнозирования.
Одним из наиболее важных классификационных признаков методов прогнозирования является степень формализации, которая достаточно полно охватывает прогностические методы. Вторым классификационным признаком можно назвать общий принцип действия методов прогнозирования, третьим - способ получения прогнозной информации.
Прежде чем перейти к детальному рассмотрению классификационных групп методов прогнозирования, необходимо определить понятие метода или методов экономического прогнозирования. Под ними следует понимать совокупность приемов и способов мышления, позволяющих на основе анализа ретроспективных данных, экзогенных (внешних) и эндогенных (внутренних) связей объекта прогнозирования, а также их измерений в рамках рассматриваемого явления или процесса вывести суждения определенной достоверности относительно его (объекта) будущего развития.
Научно обоснованная классификация дает возможность увеличить число приемов (модификаций) на нижних уровнях классификации, куда могут быть внесены новые элементы. На рис.2.1 представлена классификационная схема методов прогнозирования.
По степени формализации (по первому классификационному признаку) методы экономического прогнозирования можно разделить на интуитивные и формализованные. Интуитивные методы прогнозирования используются в тех случаях, когда невозможно учесть влияние многих факторов из-за значительной сложности объекта прогнозирования. В этом случае используются оценки экспертов. При этом различают индивидуальные и коллективные экспертные оценки.
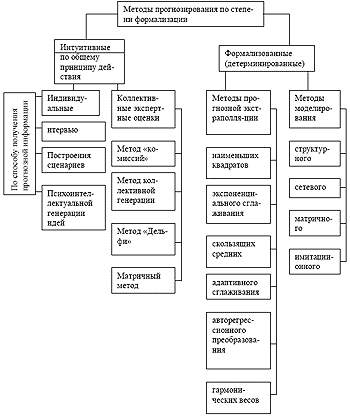
В состав индивидуальных экспертных оценок входят: метод «интервью», при котором осуществляется непосредственный контакт эксперта со специалистом по схеме «вопрос – ответ»; аналитический метод, при котором осуществляется логический анализ какой-либо прогнозируемой ситуации, составляются аналитические докладные записки; метод написания сценария, который основан на определении логики процесса или явления во времени при различных условиях.
Методы коллективных экспертных оценок включают в себя метод «комиссий», «коллективной генерации идей» («мозговая атака»), метод «Дельфи», матричный метод. Эта группа методов основана на том, что при коллективном мышлении, во-первых, выше точность результата и, во-вторых, при обработке индивидуальных независимых оценок, выносимых экспертами, по меньшей мере могут возникнуть продуктивные идеи.
В группу формализованных (детерминированных) методов входят две подгруппы: экстраполяции и моделирования. К первой подгруппе относятся методы: наименьших квадратов, экспоненциального сглаживания, скользящих средних, адаптивного сглаживания, авторегрессионного преобразования, гармонических весов; ко второй - структурное, сетевое, матричное и имитационное моделирование.
Рассмотренные классы интуитивных и формализованных методов схожи по своему составу с экспертными и «фактографическими» методами. Фактографические методы основаны на фактически имеющейся информации об объекте прогнозирования и его прошлом развитии, экспертные базируются на информации, полученной по оценкам специалистов-экспертов.
В класс экспертных методов прогнозирования входит метод эвристического прогнозирования (эвристика - наука, изучающая продуктивное, творческое мышление). Это аналитический метод, суть которого заключается в построении и последующем усечении «дерева поиска» экспертной оценки с использованием какой-либо эвристики. При этом методе осуществляется специализированная обработка прогнозных экспертных оценок, полученных путем систематизированного опроса высококвалифицированных специалистов. Он применяется для разработки прогнозов научно-технических проблем и объектов, анализ развития которых либо полностью, либо частично не поддается формализации.
Особое место в классификации методов экономического прогнозирования занимают так называемые комбинированные методы, которые объединяют различные другие методы. Например, коллективные экспертные оценки и методы моделирования или статистические и опрос экспертов.
В качестве информации используется фактографическая и экспертная информация.
При классификации методов прогнозирования необходимо иметь в виду, что содержательная систематизация методов прогнозирования должна определяться самим объектом прогнозирования, экономическими процессами развития и их закономерностями.
С точки зрения оценки возможных результатов и путей прогнозного научно-технического развития прогнозы можно классифицировать по трем этапам: исследовательскому, программному и организационному.
Задачей исследовательского прогноза является определение возможных результатов будущего развития и выбор из множества возможных вариантов одного или нескольких положительных результатов. Так, например, развитие средств вычислительной техники можно отразить в росте их быстродействия, увеличении объема памяти и диапазона логических возможностей.
Основная цель этого этапа состоит в раскрытии широкой гаммы принципиально возможных перспектив в виде одной или ряда научно-технических проблем, подлежащих решению в течение прогнозируемого периода.
Программный аспект прогноза заключается в определении возможных путей достижения желаемых и необходимых результатов; ожидаемого по времени реализации каждого из возможных варианта и степени достоверности в успешном достижении некоторого результата по тому или иному варианту.
Организационная сторона прогноза включает в себя комплекс организационно-технических мероприятий, обеспечивающих достижение определенного результата по тому или иному варианту. В организационном аспекте исходят из представления о наличных экономических ресурсах и накопленном научном потенциале. Здесь должна быть сформулирована обоснованная гипотеза развития комплекса организационных параметров науки, дана вероятностная оценка рекомендуемой схеме распределения ресурсов и перспективам роста научного потенциала на прогнозируемый период.
Рассмотренные этапы научно-технического развития, как правило, выступают комплексно и находятся во взаимосвязи.
28. Под прогнозом понимается научно обоснованное описание возможных состояний объектов в будущем, а также альтернативных путей и сроков достижения этого состояния. Процесс разработки прогнозов называется прогнозированием. Прогнозирование – вид познавательной деятельности человека, направленной на формирование прогнозов развития объекта, на основе анализа тенденций его развития. Прогнозирование должно отвечать на два вопроса: что вероятнее всего можно ожидать в будущем? Каким образом нужно изменить условия, чтобы достичь заданное состояние? Прогнозирование является важным связующим звеном между теорией и практикой во всех областях жизни общества. В зависимости от степени конкретности и характера воздействия на ход исследуемых процессов и явлений различают три формы предвидения: гипотезу (общенаучное предвидение), прогноз и план. Эти формы предвидения тесно связаны в своих проявлениях друг с другом и с исследуемым объектом в системе управления и планирования, представляют собой последовательные ступени познания поведения объекта в будущем.
Прогнозы можно подразделять в зависимости от целей, задач, объектов, времени упреждения, методов организации прогнозирования, источников информации и т. д. Большое количество таких признаков и отсутствие их строго определенных характеристик затрудняют создание единой классификации.
Задачи экономико-статистического прогнозирования следующие:
выявление перспектив ближайшего или более отдаленного будущего в исследуемой области на основе реальных процессов действительности;
выработка оптимальных тенденций и перспективных планов с учетом составленного прогноза и оценки принятого решения с позиций его последствий в прогнозируемом периоде [2, с. 117].
Статистические методы прогнозирования - научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных (в том числе непараметрических методов наименьших квадратов с оцениванием точности прогноза, адаптивных методов, методов авторегрессии и др.); развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования, в том числе методов анализа субъективных экспертных оценок на основе статистики нечисловых данных; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений. Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т.е. функции, определенной в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи - интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К.Гауссом в 1794-1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование.
Основные этапы прогнозирования и типы прогнозов
Построение прогноза и связанные с ним построение и экспериментальная проверка (верификация) вероятностно-статистической модели обычно основаны на одновременном использовании информации двух типов:
- априорной информации о природе и содержательной сущности анализируемого явления, представленной, как правило, в виде тех или иных теоретических закономерностей, ограничений, гипотез;
- исходных статистических данных, характеризующих процесс и результаты функционирования анализируемого явления или системы.
Можно выделить следующие основные этапы прогнозирования.
1-й этап (постановочный) включает в себя определение конечных прикладных целей прогнозирования; набора факторов и показателей (переменных), описание взаимосвязей между которыми нас интересует; роли этих факторов и показателей – какие из них, в рамках поставленной конкретной задачи, можно считать входными (т.е. полностью или частично регулируемыми или хотя бы легко поддающимися регистрации и прогнозу; подобные факторы несут смысловую нагрузку объясняющих в модели), а какие – выходными (эти факторы обычно трудно поддаются непосредственному прогнозу; их значения формируются как бы в процессе функционирования моделируемой системы, а сами факторы несут смысловую нагрузку объясняемых).
2-й этап (априорный, предмодельный) состоит в предшествующем построению модели анализе содержательной сущности изучаемого процесса или явления, формировании и формализации имеющейся априорной информации об этом явлении в виде ряда гипотез и исходных допущений (последние должны быть подкреплены теоретическими рассуждениями о механизме изучаемого явления или, если возможно, экспериментальной проверкой).
3-й этап (информационно-статистический) заключается в сборе необходимой статистической информации, т.е. регистрации значений участвующих в анализе факторов и показателей на различных временных и (или) пространственных тактах функционирования моделируемой системы.
4-й этап (спецификация модели) включает в себя непосредственный вывод (опирающийся на принятые на 2-м этапе гипотезы и исходные допущения) общего вида модельных соотношений, связывающих между собой интересующие нас входные и выходные переменные. Говоря об общем виде модельных соотношений, мы имеем в виду то обстоятельство, что на данном этапе будет определена лишь структура модели, ее символическая аналитическая запись, в которой наряду с известными числовыми значениями (представленными в основном исходными статистическими данными) будут присутствовать величины, содержательный смысл которых определен, а числовые значения – нет (их обычно называют параметрами модели, неизвестные значения которых подлежат статистическому оцениванию).
5-й этап (исследование идентифицируемости и идентификация модели) состоит в проведении статистического анализа модели с целью «настройки» значений ее неизвестных параметров на те исходные статистические данные, которыми мы располагаем. При реализации этого этапа «прогнозист» должен сначала ответить на вопрос, возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным статистическим данным при принятой на 4-м этапе структуре (способе спецификации) модели. Это составляет так называемую проблему идентифицируемости модели. А затем, после положительного ответа на этот вопрос, необходимо решить уже проблему идентификации модели, т.е. предложить и реализовать математически корректную процедуру оценивания неизвестных значений параметров модели по имеющимся исходным статистическим данным. Если проблема идентифицируемости решается отрицательно, то возвращаются к 4-у этапу и вносят необходимые коррективы в решение задачи спецификации модели.
6-й этап (верификация модели) заключается в использовании различных процедур сопоставления модельных заключений, оценок, следствий и выводов с действительностью. Этот этап называют также этапом статистического анализа точности и адекватности модели. При пессимистическом характере результатов этого этапа необходимо возвратиться к этапу 4, а иногда и к этапу 1. Если же этап верификации модели дает положительные результаты, то модель может быть непосредственно использована для построения прогноза в соответствии с описанной выше общей схемой.
29. График, геометрическое изображение функциональной зависимости при помощи линии на плоскости.
Статистический график - это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Представление данных таблицы в виде графика производит более сильное впечатление, чем цифры, позволяет лучше осмыслить результаты статистического наблюдения, правильно их истолковать, значительно облегчает понимание статистического материала, делает его наглядным и доступным. Это, однако, вовсе не означает, что графики имеют лишь иллюстративное значение.
Графический метод — это метод условных изображений при помощи линий, точек, геометрических фигур и других символов.
Поле графика — пространство, на котором размещаются графические символы.
Графические образы — составляют основу графика. В качестве графических символов используются геометрические знаки.
Масштаб — это мера перевода числовой величины в графическую.
Масштабная шкала — линия с нанесенными на нее масштабными отметками и их числовыми значениями. Шкалы могут быть равномерными и неравномерными (логарифмические шкалы), прямолинейными и криволинейными (круговые).
Экспликация графика — пояснения содержания графика, относящиеся к его заголовку, единицам измерения.
30. Индексы являются важнейшим видом обобщающих статистических показателей. Они используются для характеристики динамики явлений, сравнений по различным территориям, при контроле и разработке плановых заданий. Наравне со средними величинами они представляют собой один из самых распространенных видов статистических показателей. Слово «индекс» (index) в переводе с латыни означает указатель, показатель. В статистике этот термин имеет специфическое значение. Индекс – это относительная величина, характеризующая изменение сложных общественных явлений во времени, пространстве или по сравнению с планом.
Индекс является результатом сравнения двух одноименных величин, поэтому необходимо различать величину сравнения (числителя индексного отношения) и базу сравнения (знаменатель). Выбор базы сравнения определяется целью исследования; при изучении динамики в качестве базы используются данные какого-либо предыдущего периода; при контроле за выполнением плана – плановые данные; при территориальных сравнениях – данные другой территории.
Величину сравнения обычно называют показателем отчетного периода, базу сравнения называют показателем базисного периода. Если базисный уровень при исчислении индекса принимается за единицу, то индексы вычисляются в виде коэффициентов, а если базисный уровень принимается за 100, то индекс вычисляют в виде процентов. На основании вычисления можно определить, во сколько раз отчетная величина больше или меньше базисной, или на сколько процентов она больше или меньше базисной.
Статистика изучает в основном сложные экономические явления, которые состоят из элементов непосредственно несоизмеримых. Так, если электромеханический завод производит несколько видов продукции, то данные о выпуске продукции в натуральном выражении суммировать нельзя. Для того, чтобы показать общее изменение выпуска по нескольким видам продукции и вычисляются индексы. С их помощью можно дать обобщенную характеристику изменения себестоимости, цен, выпуска по нескольким видам продукции.
При всем их разнообразии экономические индексы подразделяются на индивидуальные и общие индексы.
Индивидуальным называется индекс, характеризующий изменение объема производства, объема продажи, уровня производительности труда и т.д. в отношении какого-нибудь одного продукта.
Индивидуальные индексы:
цен 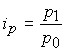 ; себестоимости ; себестоимости 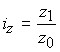 ; стоимости ; стоимости 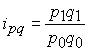 . .
31. Статистика населения - древнейшая отрасль статистической науки, которая изучает население и процессы, связанные с его динамикой, с количественной стороны в конкретных условиях общественного развития.
Объект статистики населения - совокупность людей, проживающих на определенной территории или планете в целом.
Предмет изучения этой отрасли статистики - все формы движения населения (естественное, миграционное, социальное) и закономерности его развития.
32. Население как объект статистического изучения. Источники данных о населении.
Население как предмет изучения в статистике представляет собой совокупность людей, проживающих на определенной территории и непрерывно возобновляющихся за счет рождений и смертей.
Единицей наблюдения в статистике чаще всего является отдельный человек (индивидуум), однако может быть и семья. С 1994 г. на территории СНГ стала учитываться не только семья, но и домохозяйства, как принято в международной практике. Под домохозяйством понимают совместно проживающих и ведущих общее хозяйство людей (не обязательно родственников). Домохозяйство может состоять и из одного человека, обеспечивающего себя материально.
Объектом статистического наблюдения в статистике могут быть разные совокупности: население в целом ( постоянное, наличное), определенные группы населения ( трудоспособное население, безработные, пенсионеры и т.д., мужское и женское население, городское и сельское и др.), молодые или пожилые семьи, родившиеся или умершие. Объект и единица наблюдения выбираются в зависимости от цели исследования.
Основными источниками данных о статистике населения являются: переписи (сплошные, выборочные) и текущий учет.
Основными задачами статистики населения являются:
-определение численности населения и его размещение на территории страны,
-изучение состава населения (по полу, возрасту, национальности, образованию и т.д.),
-изучение естественного движения населения,
-изучение миграции населения,
-социальная характеристика населения.
Изучение численности населения и его размещения на территории страны.
Переписи населения дают сведения о численности населения (Н) на определенную дату или на определенный момент. В промежутках между переписями численность населения определяется расчетным путем на основе данных последней переписи и данных текущей статистики о естественном (число родившихся (Р), число умерших (У) ) и механическом движении населения ( число выбывших (В), число прибывших (П) ) по балансовой схеме:
Н к.г. = Н н.г. + Р за год. - У за год + П за год - В за год
При определении численности населения отдельных населенных пунктов на определенную дату учитывают постоянное и наличное население.
Постоянное - лица, постоянно проживающие в данном пункте, включая временно отсутствующих на момент переписи.
Наличное - лица, фактически находящиеся в данном пункте на момент переписи, независимо от того является их пребывание постоянным или временным.
При учете постоянного населения выделяют временно отсутствующих и временно присутствующих.
Численность населения в любом населенном пункте в течение года изменяется, поэтому для расчета целого ряда показателей в статистике определяют среднюю численность населения за год или другой отрезок времени.
Среднегодовая численность населения ( Н ср.) обычно рассчитывается как средняя арифметическая:
Н ср. = Н н.г. + Н к.г. / 2
При наличии данных о численности населения на определенные даты ( Н1, Н2,…Нn - равностоящие) используется средняя хронологическая :
Н ср. = (ЅН1 + Н2 + … + Ѕ Нn ) / (n - 1)
В соответствии с делением населенных пунктов на городские и сельские, население по территориальному признаку подразделяется аналогично и по отдельным административно-территориальным единицам (областям, районам).
Городское население - лица, проживающие в городах и городских поселках (включая рабочие поселки и курортные города).
Сельское население - все лица, проживающие в сельской местности.
33. наличное население (лица, фактически находящиеся на момент переписи в данном населенном пункте, включая временно проживающих) и постоянное население (лица, для которых данный населенный пункт является местом постоянного проживания, включая временно отсутствующих).
В основу отечественной статистики положено деление населения на городское и сельское.
К городскому населению относятся жители городских поселений, поселков городского типа, дачных поселков.
Сельское население проживает в населенных пунктах, которые классифицируются как сельские поселения.
Возрастной анализ населения, отражающий процесс воспроизводства населения, широко используется при разработке экономической и социальной политики. Выделяются:
o лица моложе трудоспособного возраста;
o лица трудоспособного возраста;
o лица старше трудоспособного возраста.
Статистика населения включает такие единицы учета, как семья и домохозяйство. Семья как статистическая единица определяется как группа лиц, связанных родственными отношениями, проживающих на одной территории и имеющих общий бюджет.
34. виды демографических процессов
Демографический процесс - последовательность одноименных событий в жизни людей, имеющих значение для смены поколений. (Увеличивают численность: Рождаемость, Иммиграция; Уменьшают численность: Смертность, Эмиграция; Не меняют численности населения, но меняют состав: брачность, разводимость)
35. Основные показатели численности населения
Исходной базой для определения количественных характеристик трудовых ресурсов страны, региона или населенного пункта является фактическая численность населения соответствующей территории.
Численность населения относится к числу наиболее общих количественных характеристик населения и определяется на основе переписи населения, а в промежутках между ними путем расчетов численности и состава населения по данным переписи и регистрации рождений, смертей, прибытий, выбытий. Прогнозируемая численность населения на плановый период определяется методом передвижки по возрастам и экстраполяции сальдо миграции. Численность населения непрерывно меняется, поэтому возникает необходимость определения средней численности населения.
Средняя численность населения (среднее население) - обобщающий показатель численности населения для всего рассматриваемого периода, рассчитываемый, как правило, за год. Средняя численность населения за год (среднегодовая численность населения) определяется на середину года как средняя арифметическая из данных численности населения на начало и конец года или путем прибавления к начальной численности населения, половина ее годового прироста.
Показатель средней численности населения важен при оценке и анализе демографических процессов: исчисления общих коэффициентов рождаемости, смертности, естественного прироста и др. Для характеристики воспроизводства населения применяются показатели рождаемости, смертности, естественного прироста.
Рождаемость и смертность рассчитываются на 1000 чел. населения (в промилле) и измеряются с помощью систем коэффициентов и таблиц (рождаемости, смертности).
Разница между числом родившихся и умерших при положительном результате называется естественным приростом населения.
Наряду с абсолютными величинами определяются относительные показатели рождаемости, смертности, естественного прироста, называемые коэффициентами естественного движения населения. Они рассчитываются как для всего населения (общие), так и для отдельных возрастных групп, половых, социальных и др.
Общий коэффициент рождаемости n определяется по формуле:
n = ЧN/Чср.; где
ЧN - число родившихся в этот период детей;
Чср - численность населения на середину периода (среднегодовое население).
Этот показатель рассчитывается обычно в промилле.
Общий коэффициент смертности m исчисляется как отношение числа умерших Чm течение некоторого периода Чср. и средней численности населения: m = Чm/Чср.
Коэффициент естественного прироста населения К есть отношение естественного прироста населения (Р) к средней численности населения (Р ) за определенный период времени t :
К = Р/Р ;
К - коэффициент естественного прироста;
Р - естественный прирост населения;
Р - средняя численность населения;
Наряду с указанными коэффициентами рассчитываются показатели роста населения, характеризующие изменения численности населения во времени.
Средний коэффициент прироста населения
К исчисляется по формуле К = (Рn - Ро)/ nР
где: Ро - численность населения на начало года;
Рn - численность населения на конец года;
n - длительность периода, лет;
Р - средняя численность населения в периоде.
Средний темп роста населения Sp и средний темп прироста населения Sпр
Соответственно равны:
Sp = P/Po ; Sпр = (Рn/Po)x - 1
На численность населения территории влияет также механическое движение населения - миграционные потоки, их направления и т.д.
|
|
|
 Скачать 0.52 Mb.
Скачать 0.52 Mb.