Введение в математическую логику. Сочинение по формальной логике Первая Аналитика
 Скачать 32.7 Kb. Скачать 32.7 Kb.
|
|
Введение в математическую логику Математическая логика (теоретическая логика, символическая логика) — раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики. В более широком смысле рассматривается как математизированная ветвь формальной логики — «логика по предмету, математика по методу», «логика, развиваемая с помощью математических методов». Этапы развития математической логики Первое дошедшее до нас сочинение по формальной логике — «Первая Аналитика» Аристотеля (384-322 гг. до нашей эры). В нём рассматриваются основы силлогистики — правила вывода одних высказываний из других. Так из высказываний «Все люди смертны» и «Сократ — человек» можно сделать вывод, что «Сократ смертен». Однако на практике такие рассуждения встречаются крайне редко. Вопрос о создании символической логики как универсального научного языка рассматривал Лейбниц в 1666 году в работе «Искусство комбинаторики» (De arte combinatoria). Он думал о записи высказываний на специальном языке, чтобы затем по логическим законам вычислять истинность других. В середине XIX века появились первые работы по алгебраизации аристотелевой логики, сформировавшие первооснову исчисления высказываний (Буль, де Морган, Шрёдер). В работах Фреге и Пирса (конец 1870-х — начало 1880-х) в логику введены предметные переменные, кванторы и, тем самым, основано исчисление предикатов. В конце 1880-х годов Дедекинд и Пеано применили эти инструменты в попытках аксиоматизации арифметики, при этом Пеано создал удобную систему обозначений, закрепившуюся и в современной математической логике. Уайтхед и Рассел создают в 1910—1913 годах трактат Principia Mathematica, который оказал исключительное влияние на все последующее развитие математической логики. Ещё одной важной вехой в развитии логики стало обнаружение свойственных уровню развития логических исчислений и теории множеств конца XIX века парадоксов, в преодоление которых появилась концепция интуиционизма и интуиционистская логика (Брауэр, 1908) и, в качестве альтернативы, Гильбертом создана программа обоснования математики посредством аксиоматической формализации с использованием строго ограниченных средств, не приводящих к противоречиям. Разделы математической логики В Математической предметной классификации математическая логика объединена в одну секцию верхнего уровня с основаниями математики, в которой выделены следующие разделы: общая логика (англ. general logic), включает классическую логику первого порядка, логики высших порядков (логику второго порядка), комбинаторную логику, λ-исчисление, временную логику, модальную логику, многозначные логики, нечёткую логику, логику в информатике; – теория моделей; теория вычислимости и теория рекурсии; теория множеств; теория доказательств и конструктивная математика; алгебраическая логика (включает вопросы изучения булевых алгебр, алгебр Гейтинга, квантовых логик, цилиндрических и полиадических алгебр, алгебр Поста); нестандартные модели. Некоторые основные положения математической логики Применение в логике математических методов становится возможным тогда, когда суждения формулируются на некотором точном языке. Такие точные языки имеют две стороны: синтаксис и семантику. Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет. Важную роль в математической логике играют понятия дедуктивной теории и исчисления. Исчислением называется совокупность правил вывода, позволяющих считать некоторые формулы выводимыми. Правила вывода подразделяются на два класса. Одни из них непосредственно квалифицируют некоторые формулы как выводимые. Такие правила вывода принято называть аксиомами. Другие же позволяют считать выводимыми формулы A, синтаксически связанные некоторым заранее определённым способом с конечными наборами A1, …, An выводимых формул. Широко применяемым правилом второго типа является правило modus ponens: если выводимы формулы A и ( A → B ), то выводима и формула B. Отношение исчислений к семантике выражается понятиями семантической пригодности и семантической полноты исчисления. Исчисление И называется семантически пригодным для языка Я, если любая выводимая в И формула языка Я является верной. Аналогично, исчисление И называется семантически полным в языке Я, если любая верная формула языка Я выводима в И. Многие из рассматриваемых в математической логике языков обладают семантически полными и семантически пригодными исчислениями. В частности, известен результат Курта Гёделя о том, что классическое исчисление предикатов является семантически полным и семантически пригодным для языка классической логики предикатов первого порядка (теорема Гёделя о полноте). С другой стороны, имеется немало языков, для которых построение семантически полного и семантически пригодного исчисления невозможно. В этой области классическим результатом является теорема Гёделя о неполноте, утверждающая невозможность семантически полного и семантически пригодного исчисления для языка формальной арифметики. На практике множество элементарных логических операций является обязательной частью набора инструкций всех современных микропроцессоров и, соответственно, входит в языки программирования. Это является одним из важнейших практических приложений методов математической логики, изучаемых в современных учебниках информатики. Категорический силлогизм Простой категорический силлоги́зм (др.-греч. συλ-λογισμός «подытоживание, подсчёт, умозаключение» от συλ- (συν-) «вместе» + λογισμός «счёт, подсчёт; рассуждение, размышление») — дедуктивное умозаключение, состоящее из трёх простых атрибутивных высказываний: двух посылок и одного заключения. Посылки силлогизма разделяются на бо́льшую (которая содержит предикат заключения) и меньшую (которая содержит субъект заключения). По положению среднего термина силлогизмы делятся на фигуры, а последние по логической форме посылок и заключения — на модусы. Например, Всякий человек смертен (бо́льшая посылка) Сократ — человек (меньшая посылка) Сократ смертен (заключение) Структура силлогизма В силлогизм входит три термина: S — меньший термин: субъект заключения (входит также в меньшую посылку); P — больший термин: предикат заключения (входит также в большую посылку); M — средний термин: входит в обе посылки, но не входит в заключение. Подлежащие S (субъект) — то, относительно чего мы высказываем (делится на два вида): Определённое: Единичное, Частное, Множественное - Единичные [суждения] — в которых подлежащее является индивидуальным понятием. Пример: «Ньютон открыл закон тяготения» - Частное суждение — в котором подлежащим суждения является понятие, взятое в части своего объёма. Пример: «Некоторые S суть P» - Множественное суждение — это то, в котором несколько подлежащих классовых понятий. Прим: «насекомые, пауки, раки есть членистоногие» 2) Неопределённое. Прим: «светает», «больно» и т. п. Сказуемое P (предикат) — то, что мы высказываем (2 вида суждений): Повествовательные — это суждение относительно событий, состояний, процессов или деятельности скоропроходящих. Прим: «Роза в саду цветет». Описательные — когда одному или многим предметам приписывается какое-нибудь свойство. Субъектом всегда является определённая вещь. Прим: «Огонь горяч», «снег бел». Отношение между подлежащим и сказуемым: Суждения тождества — понятия субъекта и предиката имеют один и тот же объём. Пример: «всякий равносторонний треугольник есть равноугольный треугольник» Суждения подчинения — понятия с менее широким объёмом подчиняется понятию с более широким объёмом. Пример: «Собака есть домашнее животное» Суждения отношения — именно пространства, времени, отношения. Пример: «Дом находится на улице» При определении отношения между подлежащим и сказуемым важна четкая формализация терминов, поскольку бездомная собака хоть и не является домашней с точки зрения проживания в доме, все равно относится к классу домашних животных с точки зрения принадлежности по социально-биологическому признаку. То есть следует понимать, что «домашнее животное» по социально-биологической классификации в отдельных случаях может быть «недомашним животным» с точки зрения места обитания, то есть с социально-бытовой точки зрения. Классификация простых атрибутивных высказываний по качеству и количеству По качеству и количеству различают четыре вида простых атрибутивных высказываний: A — от лат. affirmo — Общие («Все люди смертны») I — от лат. affirmo — Частноутвердительные («Некоторые люди — студенты») E — от лат. nego — Общеотрицательные («Ни один из китов не рыба») O — от лат. nego — Частноотрицательные («Некоторые люди не являются студентами») Примечание. Для условного буквенного обозначения высказываний используются гласные из латинских слов affirmo (я утверждаю, говорю да) и nego (я отрицаю, говорю нет). Единичные высказывания (такие, в которых субъект является единичным термином) приравниваются к общим. Распределённость терминов в простых атрибутивных высказываниях Для характеристики соотношения объёмов субъекта и предиката используется понятие «распределённость термина». Термин считается распределенным, если его объём полностью включается в объём другого термина или полностью исключается из него. Термин считается нераспределённым, если его объём лишь частично включается в объём другого термина или частично исключается из него. Субъект всегда распределён в общем высказывании и никогда не распределён в частном высказывании. Предикат всегда распределён в отрицательных суждениях, в утвердительных он распределён тогда, когда по объёму Р<=S. В качестве предиката, в некоторых случаях, может выступать субъект. Правила простого категорического силлогизма Средний термин должен быть распределён хотя бы в одной из посылок. Термин, не распределённый в посылке, не должен быть распределён в заключении. Число отрицательных посылок должно быть равно числу отрицательных заключений. В каждом силлогизме должно быть только три термина. Фигуры и модусы Фигурами силлогизма называются формы силлогизма, отличающиеся расположением среднего термина в посылках: Фигура 1 Фигура 2 Фигура 3 Фигура 4 Бо́льшая посылка: M—P P—M M—P P—M Меньшая посылка: S—M S—M M—S M—S Заключение: S—P S—P S—P S—P Каждой фигуре отвечают модусы — формы силлогизма, различающиеся количеством и качеством посылок и заключения. Модусом простого силлогизма называется набор простых суждений, входящих в силлогизм. Модус простого силлогизма составляет три суждения. Например, в силлогизме: Все небесные тела движутся. Все планеты — это небесные тела. Все планеты движутся. Первая посылка является простым суждением вида А (общеутвердительным), вторая посылка — это тоже простое суждение вида А, и вывод в данном случае представляет собой простое суждение вида А. Поэтому рассмотренный силлогизм имеет модус ААА. Силлогизм: Все журналы — периодические издания. Все книги не являются периодическими изданиями. Все книги не являются журналами. имеет модус АЕЕ. Силлогизм: Все углероды — простые тела. Все углероды электропроводны. Некоторые электропроводники — простые тела. имеет модус ААI. Всего модусов во всех четырёх фигурах, то есть возможных комбинаций простых суждений в силлогизме, — 256. В каждой фигуре 64 модуса. Однако из всех этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность её выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные — неправильными. Модусы изучались ещё средневековыми школами, и для правильных модусов каждой фигуры были придуманы мнемонические имена: Фигура 1 Фигура 2 Фигура 3 Фигура 4 Barbara Cesare Darapti Bramantip Celarent Camestres Disamis Camenes Darii Festino Datisi Dimaris Ferio Baroco Felapton Fesapo Bocardo Fresison Ferison Примеры силлогизмов каждого типа. Barbara Все животные смертны. Все люди — животные. Все люди смертны. Celarent Ни одна рептилия не имеет меха. Все змеи — рептилии. Ни одна змея не имеет меха. Darii Все котята игривые. Некоторые домашние животные — котята. Некоторые домашние животные — игривые. Ferio Ни одна домашняя работа не весела. Некоторое чтение — домашняя работа. Некоторое чтение не весело. Cesare Ни одна здоровая еда не полнит. Все торты полнят. Ни один торт не здоровая еда. Camestres Все лошади имеют вздутие живота. Ни один человек не имеет вздутия живота. Ни один человек не лошадь. Festino Ни один ленивый человек не сдаёт экзамены. Некоторые студенты сдают экзамены. Некоторые студенты не ленивы. Baroco Все информативные вещи полезны. Некоторые сайты не полезны. Некоторые сайты не информативны. Darapti Все фрукты питательны. Все фрукты вкусны. Некоторые вкусные продукты питательны. Disamis Некоторые кружки красивы. Все кружки полезны. Некоторые полезные вещи красивы. Datisi Все прилежные мальчики в этой школе рыжие. Некоторые прилежные мальчики в этой школе — пансионеры. Некоторые пансионеры в этой школе рыжие. Felapton Ни один кувшин в этом шкафу не нов. Все кувшины в этом шкафу треснутые. Некоторые треснутые вещи в этом шкафу не новы. Bocardo Некоторые кошки бесхвосты. Все кошки — млекопитающие. Некоторые млекопитающие бесхвосты. Ferison Ни одно дерево не съедобно. Некоторые деревья зелёные. Некоторые зелёные вещи не съедобны. Bramantip Все яблоки в моём саду полезны. Все полезные фрукты зрелы. Некоторые зрелые фрукты — яблоки в моём саду. Camenes Все яркие цветы ароматны. Ни один ароматный цветок не выращен в помещении. Ни один выращенный в помещении цветок не ярок. Dimaris Некоторые небольшие птицы питаются мёдом. Все питающиеся мёдом птицы цветные. Некоторые цветные птицы небольшие. Fesapo Ни один человек не совершенен. Все совершенные существа мифические. Некоторые мифические существа не люди. Fresison Ни один компетентный человек не ошибается. Некоторые ошибающиеся люди работают здесь. Некоторые работающие здесь люди некомпетентны. В соответствии с правилами, формы могут быть преобразованы в другие формы, и все формы могут быть преобразованы в одну из форм первой фигуры. История силлогистики Учение о силлогизме впервые изложено у Аристотеля в его «Первой аналитике». Он говорит лишь о трёх фигурах категорического силлогизма, не упоминая о возможной четвёртой. Особенно подробно он рассматривает роль модальности суждений в процессе умозаключения. Преемник Аристотеля, основатель ботаники Теофраст, по словам Александра Афродизийского (в его комментарии к первой «Аналитике» Аристотеля), прибавил ещё пять модусов (modi) к первой фигуре силлогизма; эти пять модусов впоследствии были выделены Клавдием Галеном (жившим во II-м в. н. э.) в особую четвёртую фигуру. Кроме того, Теофраст и его ученик Евдем занялись анализом условного и разделительного силлогизмов. Они допустили пять видов умозаключений: два из них соответствуют условному силлогизму, а три — разделительному, который они рассматривали как видоизменение условного силлогизма. Этим и заканчивается развитие учения о силлогизме в древности, если не считать того добавления, которое сделали стоики в учении об условном силлогизме. По словам Секста Эмпирика, стоики признавали некоторые виды условного и разделительного силлогизма αναπόδεικτοι, то есть не нуждающимися в доказательствах, и рассматривали их как прототипы силлогизма (как, например, смотрит на силлогизм Зигварт). Стоики признавали пять видов подобных силлогизмов, совпадающих с Теофрастовыми. Секст Эмпирик приводит следующие примеры для этих пяти видов: Если наступил день, то имеется свет; но теперь день, следовательно, имеется свет. Если наступил день, то имеется свет, но света нет, следовательно, нет и дня. Не может быть (одновременно) дня и ночи, но день наступил, следовательно, нет ночи. Может быть или день, или ночь, но теперь день, следовательно, нет ночи. Может быть или день, или ночь, но ночи нет, следовательно, теперь день У Секста Эмпирика и скептиков вообще мы встречаемся и с критикой силлогизма, но цель критики — доказательство невозможности доказательства вообще, в том числе и силлогистического. Схоластическая логика ничего существенного не добавила к учению о силлогизмах; она лишь порвала ту связь с теорией познания, которая существовала у Аристотеля и тем превратила логику в чисто формальное учение. Образцовым руководством логики в средние века было сочинение Марциана Капеллы, образцовым комментарием — сочинения Боэция. Некоторые из комментариев Боэция занимаются специально учением о силлогизмах, например «Introductio ad categoricos syllogismos», «De syllogismo categorico» и «De syllogismo hypothetico». Сочинения Боэция имеют некоторое историческое значение; они способствовали также установлению логической терминологии. Но в то же самое время именно Боэций придал учениям логическим характер чисто формальный. И 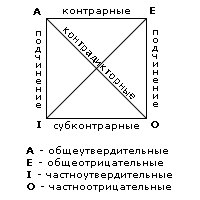 з эпохи схоластической философии по отношению к учению о силлогизме внимания заслуживает Фома Аквинский (ум. 1274), в особенности его подробный анализ ложных умозаключений («De fallaciis»). Сочинение по логике, имевшее некоторое историческое значение, принадлежит византийцу Михаилу Пселлу. Он предложил так называемый «логический квадрат», в коем наглядно выражается отношение различных видов суждений. Ему принадлежат названия различных modi (греч. τρόποι) фигур. Эти названия, латинизированные, перешли в западную логическую литературу. з эпохи схоластической философии по отношению к учению о силлогизме внимания заслуживает Фома Аквинский (ум. 1274), в особенности его подробный анализ ложных умозаключений («De fallaciis»). Сочинение по логике, имевшее некоторое историческое значение, принадлежит византийцу Михаилу Пселлу. Он предложил так называемый «логический квадрат», в коем наглядно выражается отношение различных видов суждений. Ему принадлежат названия различных modi (греч. τρόποι) фигур. Эти названия, латинизированные, перешли в западную логическую литературу.Михаил Пселл, следуя Теофрасту, пять modi четвёртой фигуры относил к первой. Название видов имело у него в виду мнемонические цели. Ему же принадлежит и общеупотребительное обозначение буквами количества и качества суждений (а, е, i, о). Учения логические у Пселла носят формальный характер. Сочинение Пселла было переведено Уильямом из Шервуда и получило распространение благодаря переделке Петра Испанского (папы Иоанна XXI). У Петра Испанского в его учебнике заметно то же стремление к мнемотехническим правилам. Латинские названия видов фигур, приводимые в формальных логиках, взяты у Петра Испанского. Пётр Испанский и Михаил Пселл представляют собой расцвет формальной логики в средневековой философии. С эпохи Возрождения начинается критика формальной логики и силлогистического формализма. Первым серьёзным критиком Аристотелевской логики был Пьер Рамэ, погибший во время Варфоломеевой ночи. Во второй части его «Диалектики» говорится о силлогизме; учение его о силлогизме, однако, существенных отступлений от Аристотеля не представляет. Начиная с Бэкона и Декарта философия идёт по новым путям и отстаивает методы исследования: непригодность силлогистического метода в смысле метода получения нового знания становится всё более и более очевидной. Тем не менее, решение силлогизмов составляет важнейшую часть любого учебника по традиционной логике. Несмотря на то, что использование силлогизмов само по себе не даёт новое знание, использование правил построения силлогизмов позволяет избежать логических ошибок, софизмов, в рамках имеющегося знания. |
