Криптосистем основанные на эллиптических кривых. Содержание реферат
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
ЗАКЛЮЧЕНИЕ В ходе данной работы были изложены базовые понятия теории эллиптических кривых, необходимые для реализации криптографических алгоритмов, а в последствие и протоколов. Мною были рассмотрены основные алгоритмы арифметики точек эллиптической кривой, а также способы генерации ключей, пригодных для использования в криптографических алгоритмах. В течении данной работы было выявлено главное преимущество эллиптической криптографии над остальными способами криптографии ныне известных для программистов. Таким преимуществом является малый размер ключа относительно других схем асимметричного шифрования. Это свойство особенно важно при реализации криптографических протоколов в условиях ограниченности ресурсов памяти и производительности. Также ясно, что с улучшением производительности компьютеров шифры постепенно будут становиться все более уязвимыми при малых длинах ключа. А с увеличение длины ключа преимущества схем на эллиптических кривых над другими схемами шифрования возрастает многократно. За счет меньшей длины ключа возрастает и эффективность вычислительных процессов. Так как в моей работе я исследовал эллиптические кривые над бинарным конечным полем, то можно сказать что этот вид кривых является наиболее лучшим для реализации на компьютерах, потому что обработка данных происходит быстрее из-за того, что компьютер лучше преобразовывает числа, которые могут быть представлены в виде степени двойки. Также следует отметить, что помимо общих алгоритмов арифметики эллиптических кривых, существует много специфических алгоритмов, разработанных для кривых специального вида, которые позволяют добиться еще большего преимущества в эффективности. В работе обосновано применение эллиптических кривых для решения задач связанных с криптографией. Приведены теоретические и практические примеры по использованию алгоритмов криптографии. Важным является тот факт, что выбранные эллиптические кривые раньше не были реализованы в алгоритмах шифрования. Они вносят простоту в реализацию алгоритмов на машинном коде. В результате проведенного исследования были решены следующие задачи: 1. Рассмотрены основные понятия криптографических методов защиты информации 2. Проанализированы современные виды атак и угрозы безопасности информационных системы 3. Изучены математические аспекты формирования эллиптических кривых, проанализированы методы оценки криптостойкости кривых; 4. На основе проделанного анализа реализованы алгоритмы криптографии. СПИСОК ЛИТЕРАТУРЫ Баричев С.Г., Серов Р.Е. Основы современной криптографии: Учебное пособие. - М.: Горячая линия - Телеком, 2002. Болотов А.А., Гашков С.Б., Фролов А.Б. Элементарное введение в эллиптическую криптографию. Протоколы криптографии на эллиптических кривых. -М.: КомКнига, 2006. Варновский Н. П.. Математическая криптография. Несколько этюдов. - М., 2003, с. 98–121. Василенко О. Н.. Теоретико-числовые алгоритмы в криптографии. МЦНМО, М., 2013 (1-е изд.) Гатчин Ю.А., А. Г. Коробейников. Основы криптографических алгоритмов Учебное пособие. СПб: ГИТМО (ТУ), 2012. 29 с. Грушо А.А., Применко Э.А., Тимонина Е.Е. Анализ и синтез криптоалгоритмов. КУРС ЛЕКЦИЙ. 2010 год. ElCamal. A public-key cryptosystem and a signature scheme based on discrete logarithms. IEEE Transaction on Informatoin Theory, 2005 Жданов О.Н., Чалкин В.А. Эллиптические кривые. Основы теории и криптографические приложения. -М.: Кн. дом «ЛИБРОКОМ», 2012. Жельников В. Криптография от папируса до компьютера. – М.: ABF, 2006. – 336с. Жиль Брассар. Современная криптология. Руководство. Пер. с англ. М.: "Полимед", 2009. - 176 с Долгов, В.А. Криптографические методы защиты информации : учеб. пособие / В.А. Долгов, В.В. Анисимов. – Хабаровск : Изд-во ДВГУПС, 2008. – 155 с. Оков И.Н. Криптографические системы защиты информации. – СПб.: ВУС, 2001. – 236с. Осипян В.О. Осипян. К.В. Криптография в задачах и упражнениях. 2004 год. Панасенко С.П. Алгоритмы шифрования. Специальный справочник. – СПб.: БХВ-Петербург, 2009 – 576 с. Птицын. Приложение теории детерминированного хаоса в криптографии. 2002 год, Погорелов, Б.А. Об определении основных криптографических понятий / Б.А. Погорелов, А.В. Черемушкин, С.И. Чечета // Доклад на конференции "Математика и безопасность информационных технологий" (МаБИТ-03, МГУ, 23-24 октября 2003 г.). Рябко Б.Я., Фионов А.Н. Криптографические методы защиты информации. - М.: Горячая линия - Телеком, 2005. Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях/ Под ред. В.Ф. Шаньгина. – М.: Радио и связь, 2001. – 376с. Ростовцев, Е.Б. Маховенко. Теоретическая криптография. 2005 год. Рихтер Дж. Windows для профессионалов: создание эффективных Win32 приложений с учетом специфики 64-разрядной версии Windows / Дж.Рихтер. — Пер, англ 4-е изд. - СПб; Питер; М.: 2001. -752 е. Смарт Н.Г. Криптография. -М.: Техносфера, 2005. Соловьев Ю.П. и др. Эллиптические кривые и современные алгоритмы теории чисел. -Москва-Ижевск: Ин-т компьютерных исследований, 2003. Семенов, Г. Цифровая подпись. Эллиптические кривые /Г. Семенов // Открытые системы. — 2002. №7;8. Тилборг Х. К. А. ван. Основы криптологии. Профессиональное руководство и интерактивный учебник. – М., Мир, 2006. Кассами Т., Токура Н., Ивадари Е., Инагаки Я. Теория кодирования/ Пер. с япон. под ред. Б. С. Цыбакова и С. И. Гельфанда. – М.: Мир, 2008. – 576с. Коблиц Н. Курс теории чисел и криптографии — Москва: Научное изд-во ТВП, 2001. — 254 c. Корниенко, А.А. Средства защиты информации на железнодорожном транспорте (Криптографические методы и средства) : учеб. пособие / А.А. Корниенко, М.А. Еремеев, С.Е. Ададуров. – М. : Маршрут, 2005. – 254 с. Коутинхо. Введение в теорию чисел. Алгоритм RSA. 2001 год. Кнепп Э. Эллиптические кривые. -М.: Факториал Пресс, 2004. Комова, О.С. Знакомство с криптографическими методами защиты информации : метод. указания / О.С. Комова. – Хабаровск : Изд-во ДВГУПС, 2010. – 28 с. Коробейников А.Г. Математические основы криптологии / А.Г. Коробейников, Ю.А.Гатчин. Учебное пособие. СПб: СПб ГУ ИТМО, 2004. 109 с. Koblitz N. A course in number theory and cryptography. Graduate texts in math. 114 New-York: Springer-Verlag, 2004. Ленг С. Эллиптические функции - М.: Наука, 2004. — 312 с. Лунин, А.В. Перспективы развития и использования асимметричных алгоритмов в криптографии / А.В. Лунин, А.А. Маховенко, Е.Б. Теоретико-числовые методы в криптографии : учеб. пособие / Е.Б. Маховенко. – М. : Гелиос АРВ, 2006. – 320 с. Myasnikov A., Shpilrain V., Ushakov A. Group-based cryptography.Advanced courses in mathematics CRM Barselona. Basel-Boston-Berlin: Birkhauser, 2008. 183 с. Фомичев В.М. Дискретная математика и криптология. Курс лекций. 2003 год. Черемушкин А.В. Лекции по арифметическим алгоритмам криптографии. 2002 год, Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. Издательство ТРИУМФ, М., 2002. Lehmann, F. Counting the number of points on elliptic curves over finite fields of characteristic greater than three / F. Lehmann, M. Maurer, V. Miiller, V. Shoup // Lecture Notes In Computer Science. 2004. - Vol. 877. - P.60-70. Lencier, R. Counting the number of points on elliptic curves over finite fields: strategies and performances / R. Lencier, F. Morain // Lecture Notes in Computer Science. 2005. - Vol. 921. - P. 79-94. Lencier, R. Finding good random elliptic curves for cryptosystems defined F2n / R. Lencier // Lecture Notes in Computer Science. 2007. -Vol.1233.-P.379-392. Madsen, M. S. A general framework for p-adic point counting and application to elliptic curves on Legendre / M. S. Madsen. // Aarhus Univ. Mat. Inst, (prepr.ser) 2004. - N 2-04. - 18 p. Menezes, A. Reducing elliptic curve logarithms to logarithms in a finite field / A. Menezes, T. Okamoto, S. Vanstone // IEEE Transactions on Information Theory. 2003. - Vol.39. - P. 1639-1646. Menezes A., Elliptic Curve Public Key Cryptosystems / A.Menezes. Kluwer Academic Publishers, Boston, 2003. Miller, V. Elliptic Curve and their Use in Cryptography / V. Miller // Proc. of PKC'97, Springer-Verlag, 2017. Mueller, V. On the generation of Cryptographically Strong Elliptic Curves / V. Mueller, S. Paulus. Technical Report, Technical University of Darmstadt, 2017. Oorschot, P.C. Parallel collision search with cryptanalitic application / P.C. van Oorschot, M.J. Wiener // J. Cryptology. 2009. - Vol.12. - P. 1-28. Pollard, J.M. Monte Carlo methods for index computation (mod p) / J.M. Pollard//Math. Сотр. 2008. -V. 32 (143).-P. 918-924. Popov, V. Additional Cryptographic Algorithms for Use with GOST 28147-89, GOST R 34.10-94, GOST R 34.10-2001, and GOST R 34.1194 Algorithms / V. Popov, I. Kurepkin, S. Leontiev. RFC 4357, January 2006. ПРИЛОЖЕНИЕ А Алгоритм шифрования и дешифрования Эль-Гамаля, Алгоритм шифрования и дешифрования Диффи-Хеллмана. Входные параметры – текст из файла Выходные параметры – расшифрованный текст Алгоритм Атаки на выбранные алгоритмы 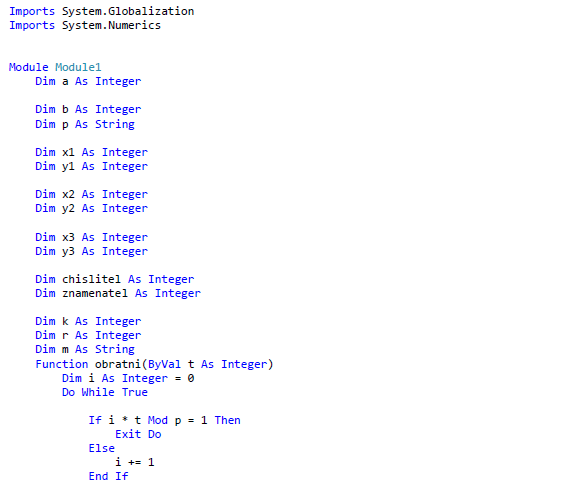  ПРИЛОЖЕНИЕ А (продолжение)   ПРИЛОЖЕНИЕ А (продолжение)  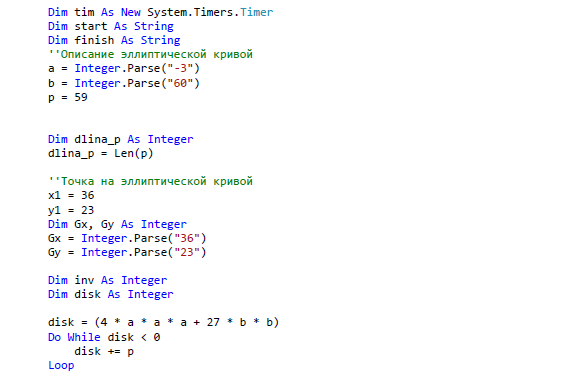 ПРИЛОЖЕНИЕ А (продолжение) 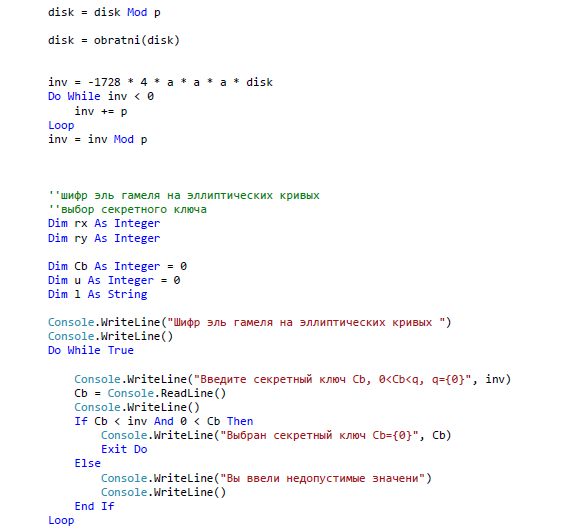 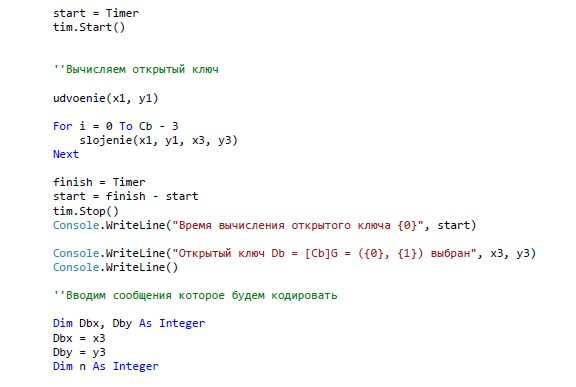 ПРИЛОЖЕНИЕ А (продолжение) 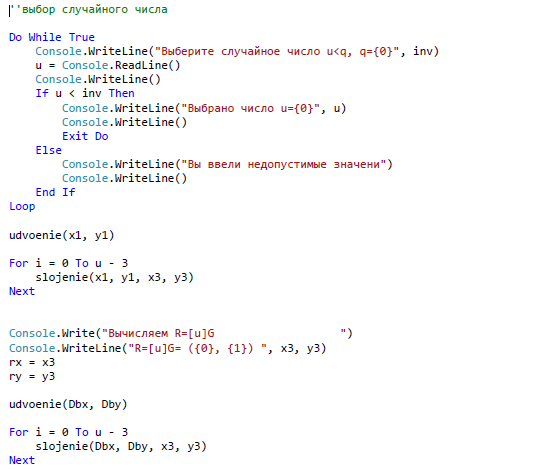  ПРИЛОЖЕНИЕ А (продолжение)  ПРИЛОЖЕНИЕ А (продолжение) 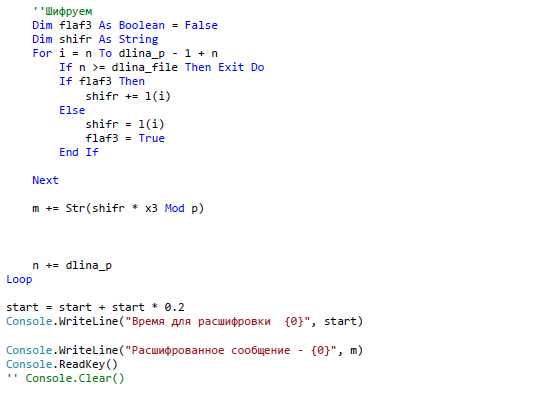 ПРИЛОЖЕНИЕ А (продолжение)  ПРИЛОЖЕНИЕ А (продолжение)   ПРИЛОЖЕНИЕ А (продолжение) 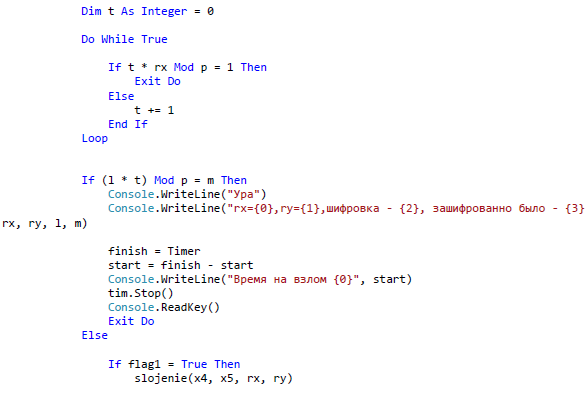 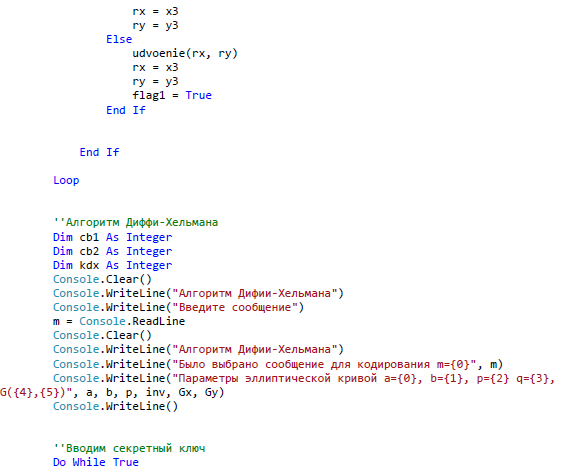 ПРИЛОЖЕНИЕ А (продолжение) 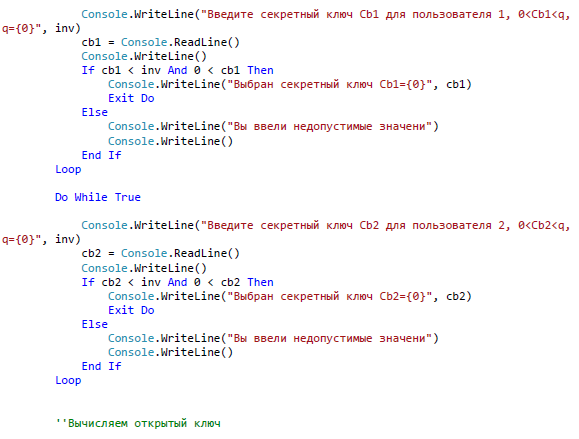 ПРИЛОЖЕНИЕ А (продолжение) 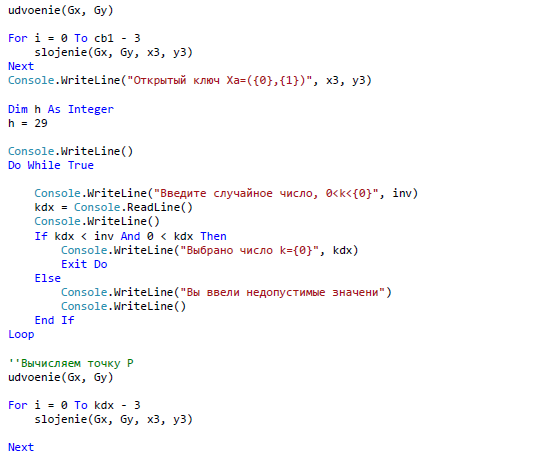  |
