Криптосистем основанные на эллиптических кривых. Содержание реферат
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
2.2. Преимущества алгоритмов криптосистемы с открытым ключом 1. Главное преимущество асимметричных шифров над симметричными шифрами заключается в том, что нет необходимости предварительно передавать секретные ключи по зашифрованному каналу связи между пользователями. 2. В симметричных алгоритмах криптографии ключ содержится в секрете для обеих пользователей, а в асимметричной криптосистеме есть только один секретный ключ. 3. При симметричном шифровании желательно обновлять ключ после каждой передачи данных, а в асимметричных криптосистемах их можно не менять достаточно долгое время. 2.3. Недостатки алгоритмов криптосистемы с открытым ключом 1. В симметричные алгоритмы шифрования достаточно легко внести изменения нежели в алгоритмы с несимметричным шифрованием. 2. Факт передачи сообщения по каналу связи может выявить как получателя, так и отправителя, даже если сообщения надежно шифруются. 3. Несимметричные алгоритмы используют ключи большие по длине, чем симметричные (таблица 2.1). Таблица 2.1
4. Требуются существенно бо́льшие вычислительные ресурсы, поэтому на практике асимметричные криптосистемы используются в сочетании с другими алгоритмами: - для ЭЦП сообщение предварительно подвергается хешированию, а с помощью асимметричного ключа подписывается лишь относительно небольшой результат хеш-функции; - для шифрования они используются в форме гибридных криптосистем, где большие объёмы данных шифруются симметричным шифром на сеансовом ключе, а с помощью асимметричного шифра передаётся только сам сеансовый ключ. 2.4. Преимущества криптосистем на эллиптических кривых Теория эллиптических кривых над конечными полями в настоящее время все больше начинает применяться в криптографии. Основная причина этого состоит в том, что эллиптические кривые над конечными полями доставляют неисчерпаемый источник конечных абелевых групп, которые удобны для вычислений и обладают богатой структурой. [8] Во многих отношениях эллиптические кривые – естественный аналог мультипликативных групп полей, но более удобный, так как существует большая свобода в выборе эллиптической кривой, чем в выборе конечного поля. [7] Большинство продуктов и стандартов, в которых для шифрования и проверки подлинности применяются методы криптографии с открытым ключом, базируется на алгоритме RSA. [3] Однако длина ключа, необходимая для успешной защиты данных при использовании алгоритма шифрования RSA за последние годы резко увеличилось, что обусловило соответствующий рост загрузки систем, использующих RSA. Криптография на основе эллиптических кривых (ECC – Elliptic Curve Cryptography) – появившийся сравнительно недавно подход, способный конкурировать с RSA. [4] Большое отличие шифрования при помощи эллиптических кривых в сравнении с RSA заключается в том, что с использованием эллиптических кривых обеспечивается эквивалентный уровень защиты при меньшей длине ключей, вследствие чего уменьшается нагрузка на ЦП. Хотя эллиптическая криптография уже давно у всех на слуху, реализованных алгоритмов, которые могли бы заменить старые методы защиты информации, достаточно мало. 2.5. Использование криптосистем на эллиптических кривых Эллиптические кривые используются в криптографии уже достаточно давно в качестве в качестве основы для построения криптосистем. Но на данный момент криптосистемы на эллиптических кривых служат для создания электронно-цифровой подписи, а для шифрования применяются мало. В своей работе я буду исследовать эффективность применения подобной криптосистемы именно для шифрования. Существует несколько основных криптосистем, в основе которых лежат эллиптические кривые: 1. ECDSA алгоритм, основывающийся на электронно-цифровой подписи. 2. ECDH алгоритм, основывающийся на алгоритме Диффи-Хеллмана. 3. ECMQV алгоритм, основывается на протоколе распределения ключей Менезеса-Кью-Венстоуна. 4. ГОСТ Р 34.10-2001 Криптосистемы, основанные на ЭК могут применяться в различных областях, таких как: - сфера мобильных устройств - пластиковые карты - электронная торговля и банковские операции - интернет-приложения - протоколы передачи данных 2.6.Некоторые проблемы и трудности в использовании систем на основе эллиптической кривой Главная проблема состоит в том, что истинная сложность ECDLP ещё не осознана полностью. Недавнее исследование показало, что некоторые использовавшиеся для отработки алгоритмов шифрования эллиптические кривые, фактически не подходят для таких операций. Например, если координаты базовой точки P равны положению p, то ECDLP имеет простое решение. Такие кривые являются “аномальными” кривыми. Исследования в этой области продолжаются по сей день, но потенциальные пользователи все еще проявляют осторожность и выжидают. Несовместимые системы.Хотя “четные” и “нечетные” эллиптические кривые подобны, они все же различаются настолько, что “нечетная” система гарантированно несовместима с “четной” системой. Кроме того, в случае “четной” системы существуют различные способы представления кривых и базовых точек, причем пользователи систем с разными способами представления не имеют возможности связаться друг с другом Это отличает системы на основе эллиптических кривых от систем RSA, которые теоретически являются совместимыми. Несмотря на проблему совместимости, “четные” системы эллиптической кривой имеют весомые преимущества благодаря эффективности, которая достигается главным образом за счет скорости обработки. Но и здесь пользователи должны быть осторожны. Множество экспертов в этой области полагают, что “четные” случаи ECDLP более просты для решения чем “нечетные”, хотя надо признать, что такие утверждения безосновательны. Проблема лицензирования и патентования криптосистем на основе эллиптической кривой еще не решена. В этой области существует множество патентов, но главным образом для применения в частных случаях. 3 ГЛАВА. СИСТЕМНЫЙ АНАЛИЗ ЗАДАЧИ 3.1. Выбор точки и размещение данных Использование группы точек эллиптической кривой в криптографии связано с выбором определенных ее точек. При этом в зависимости от криптографической задачи выбирают точку случайно или точку, координаты которой отражают данные, помещаемые на кривую. Так бинарный вектор, представляющий значение координаты x, может содержать как часть данную бинарную подпоследовательность x 0 , значение координаты y при этом определяется по уравнению кривой. Последнее связано с решением квадратного уравнения определённого вида. Далее рассматриваются методы решения квадратных уравнений, возникающих при вычислении координаты y точки эллиптической кривой, а затем — методы размещения данных на кривой. Суперсингулярный случай. Рассмотрим квадратное уравнение Y2 + Y = σ, (3.1) где σ – элемент поля GF(2n), такой, что T r(σ) = 0. (Если Tr(σ) = 1, то уравнение не имеет решения. Нетрудно видеть, что если y – корень этого уравнения, то y + 1 – второй его корень, так как y 2 + y = y(y + 1). Решение y как элемент поля GF(2n) можно представить в полиномиальном базисе в виде вектора (y0, y1, . . . , yn−2, yn−1), а также в виде многочлена – произведения этого вектора коэффициентов на покомпонентное произведение единичной матрицы T1 и вектора степеней корня λ неприводимого многочлена: 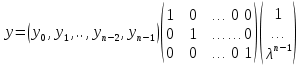 (2.2) (2.2) Это матричное представление эквивалентно полиномиальному представлению y = y0 · λ 0 + y1 · λ 1 + . . . + yi · λ i + . . . + yn−2 · λ n−2 + yn−1 · λ n−1 3.2. Выбор основного поля Fq и эллиптической кривой E При выборе поля эллиптической кривой для шифрования, имеются три основных пункта, которые должны быть сделаны: 1. Выбор основного конечного поля Fq. Обычно выбираются два наиболее общих варианта основного конечного поля для реализации алгоритмов - F2m и Fq. Где поле F2m – бинарное конечное поле, а Fq поле конечное поле, где q – простое число. [12] В моем диссертационной работе я решила сравнить то, как будут работать алгоритмы на эллиптических кривых, если выбрать в качестве поля сначала бинарное, а потом простое. 2. Выбор представления для элементов Fq. Если поле F2m выбрано как основное конечное поле, то имеются много путей, в которых элементы F2m могут быть представлены. Два наиболее эффективных пути: нормальное представление основания и полиномиальное представление основания. [13] 3. Выбор эллиптической кривой E по полю Fq В большенстве случаев выбираются несуперсингулярные эллиптические кривые. При выборе несуперсингулярной эллиптической кривой, можно выбирать кривую наугад, или можно выбирать кривую специальными свойствами, которые могут привести к увеличению скорости эллиптической арифметике на кривой. 3.3. Реализация математического аппарата эллиптической кривой Наряду с фундаментальными алгебраическими аспектами эллиптических кривых особое внимание уделяется вопросам эффективной реализации базовых операций основанных на них криптографических протоколов с учетом особенностей и возможностей компьютера. [10] По существу, речь идет о расширении его функциональных возможностей позволяющем эффективную реализацию операций в конечных полях и в группах точек эллиптических кривых. Это расширение допускает как чисто программные, так и технические, па основе синтеза логических схем. решения. Я использовал все возможности достижения высокой скорости выполнения операции, как чисто программные, так и принципиально алгоритмические. Приемы первого рода - программными «трюками», они позволяют повышать скорость выполнения операций «в разы», то есть уменьшают константу в оценке сложности операции. К таким «трюкам» относится, например, табулирование некоторых операции над байтами (умножение, возведение в квадрат, подсчет числа единиц, вычисление частного от деления на многочлен 1+х, метод ускорения приведения по модулю неприводимого «малочлена» и другие). Разработка велась на VB, для того чтобы сохранить универсальность и сравнимость реализации алгебраических преобразовании. 3.4. Формирование ключей алгоритма Эль-Гамаля Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом, основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи. Схема Эль-Гамаля лежит в основе бывших стандартов электронной цифровой подписи в США (DSA) и России (ГОСТ Р 34.10-94). Схема была предложена Тахером Эль-Гамалем в 1985 году. Эль-Гамаль разработал один из вариантов алгоритма Диффи-Хеллмана. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и для обеспечения аутентификации. В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой, так как не требовалась оплата взносов за лицензию. Считается, что алгоритм попадает под действие патента Диффи-Хеллмана. Секретным ключом может являться любое натуральное число x. Для определения открытого ключа вычисляется число у по формуле (3.1): у = 𝑔𝑥(𝑚𝑜𝑑 𝑝) (3.1) Группа чисел (p,g,y) – открытый ключ. Шифрование Сообщение в этой системе представляется как элемент m. Для его шифрования поступают следующим образом: 1. Генерируют случайный ключ k – взаимнопростой с p – 1, что 1 ≤ k ≤ p – 1; 2. Вычисляют 𝐶1 = 𝑔𝑘(𝑚𝑜𝑑 𝑝); 3. Находят С2 = 𝑚×𝑦𝑘(𝑚𝑜𝑑 𝑝); 4. Выдают получившийся шифротекст в виде пары С = (C1,С2). Заметим, что при каждом шифровании применяется свой кратковременный ключ. Поэтому, шифруя одно сообщение дважды, мы получаем разные шифротексты. Дешифрование Чтобы расшифровать пару данных С = (C1,C2), производят следующие преобразования: (𝐶2/𝐶1𝑥)(𝑚𝑜𝑑 𝑝) = ((𝑚×𝑦𝑘)/𝑔𝑘𝑥) (𝑚𝑜𝑑 𝑝)= (𝑚×𝑔𝑘𝑥)/𝑔𝑘𝑥 =𝑚. (3.2) Формула (3.2) является доказательством того, что преобразование является верным. Достоинства системы Эль-Гамаль: 1. Каждый пользователь системы должен выбрать случайное число и сделать не сложное вычисление, которая требует, чтобы каждый пользователь системы находил два больших простых числа, что является сложной вычислительной задачей. 2. Каждый раз при шифровании используем свой кратковременный ключ. 3. При заданном уровне стойкости алгоритма целые числа, участвующие в вычислениях, имеют запись на 25% короче, что уменьшает сложность вычислений почти в два раза и позволяет заметно сократить объем используемой памяти (рисунок 3.1). Рисунок 3.1 Схема шифрования 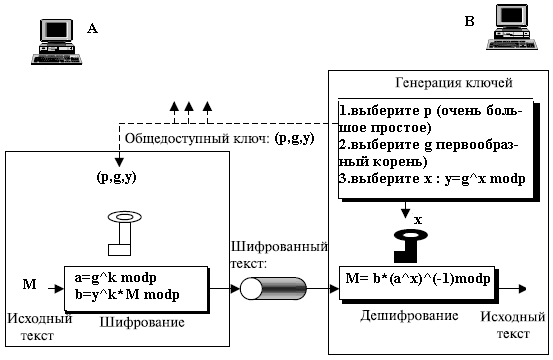 Так как в схему Эль-Гамаля вводится случайная величина k, то шифр Эль-Гамаля можно назвать шифром многозначной замены. Из-за случайности выбора числа k такую схему еще называют схемой вероятностного шифрования. Вероятностный характер шифрования является преимуществом для схемы Эль-Гамаля, так как у схем вероятностного шифрования наблюдается большая стойкость по сравнению со схемами с определенным процессом шифрования. Недостатком схемы шифрования Эль-Гамаля является удвоение длины зашифрованного текста по сравнению с начальным текстом. Для схемы вероятностного шифрования само сообщение M и ключ не определяют шифротекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины k для шифровки различных сообщений M и M'. Если использовать одинаковые k, то для соответствующих шифротекстов (a,b) и (a',b') выполняется соотношение b(b')-1=M(M')-1 b(b')-1=M(M')-1. Из этого выражения можно легко вычислить M', если известно M. Цифровая подпись служит для того чтобы можно было установить изменения данных и чтобы установить подлинность подписавшейся стороны. Получатель подписанного сообщения может использовать цифровую подпись для доказательства третьей стороне того, что подпись действительно сделана отправляющей стороной. При работе в режиме подписи предполагается наличие фиксированной хеш-функции h(.), значения которой лежат в интервале (1, p-1) (рисунок 3.1). Рисунок 3.2 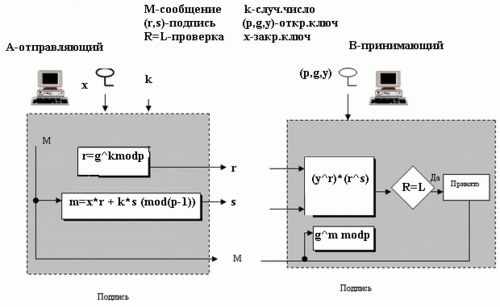 Для подписи сообщения M выполняются следующие операции: Вычисляется дайджест сообщения M:m=h(M).(Хеш функция может быть любая). Выбирается случайное число 1 Вычисляется число s=(m-xr)k-1, где k в степени минус 1 это мультипликативное обратное. Подписью сообщения M является пара (r,s). Таблица 3.1 Сравнение некоторых алгоритмов:
Криптостойкость определяется сложностью нахождения индекса, свя- зывающего два элемента группы точек на кривой. При этом алгоритм явля- ется стойким, если в разложении порядка группы на простые множители встречается большой простой делитель. Поэтому при оценивании сложно- сти анализа криптоалгоритмов важным является вычисление порядка груп- пы с последующим разложением его на простые множители. Если сравнить сложность факторизации целых чисел в задаче дискретного логарифмирования и в системах, основанных на ЭК, то последние выглядят предпочтительнее. Например, сложность задачи на ЭК при разрядности p в 128 бит соответствует задаче разложения чисел и дискретного логарифмирования с разрядностью 512 бит. Выигрыш в стойкости особенно заметен при больших размерах ключа. Данное обстоятельство позволяет использовать криптографические конструкции подобного типа для построения криптографических протоколов различного назначения. Сложность нахождения индекса в зависимости от исходного поля и степени расширения поля, куда отображается группа кривых, представлена в табл. 2. Таблица 3.2 Трудоемкость дискретного логарифма на ЭК по времени
Из табл. 2 видно, что степень расширения l = 2 обеспечивает сравни- мую сложность при малых размерах ключа. |
