Криптосистем основанные на эллиптических кривых. Содержание реферат
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
3.5. Алгоритм шифрования Деффи-Хеллмана Схема обмена ключами Диффи — Хеллмана, изобретённая в 1976 году Уитфилдом Диффи и Мартином Хеллманом под влиянием работ Ральфа Меркле (Ralph Merkle), стала первым практическим методом для получения общего секретного ключа при общении через незащищенный канал связи. Годом позже был изобретен первый алгоритм асимметричного шифрования RSA, который решил проблему общения через незащищённый канал кардинально, уже не требуя, чтобы каждая сторона имела копию одного и того же секретного ключа. Предположим, что обоим абонентам известны некоторые два числа g и p, которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение A = gamod p и пересылает его второму, а второй вычисляет B = gbmod p и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение Bamod p = gabmod p, а второй абонент на основе имеющегося у него b и полученного по сети A вычисляет значение Abmod p = gabmod p. Как нетрудно видеть, у обоих абонентов получилось одно и то же число: K = gabmod p. Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления gabmod p по перехваченным gamod p и gbmod p, если числа p,a,b выбраны достаточно большими. Рисунок 3.3 Алгоритм Диффи — Хеллмана 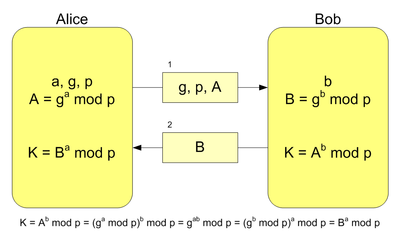 где K — итоговый общий секретный ключ. При работе алгоритма каждая сторона: 1. Пользователь 1 генерирует случайное число a, которое является закрытым ключом 2. Совместно с удалённой стороной устанавливает открытые параметры p и g такие, что: p является случайным простым числом. (p-1)/2 также должно быть случайным простым g является обратным числом по модулю p 3. Вычисляет открытый ключ A по формуле (3.3) 𝐴 = 𝑔∗𝑎 𝑚𝑜𝑑 𝑝 (3.3) 4. Пользователи обмениваются ключами 5. Вычисляет общий секретный ключ K по формуле (3.4) 𝐾 = 𝐵∗𝑎 𝑚𝑜𝑑 𝑝 (3.4) Общий секретный ключ будет равным для обоих пользователей так как: 𝐵∗𝑎 𝑚𝑜𝑑 𝑝 = (𝑔𝑏 𝑚𝑜𝑑 𝑝)𝑎 𝑚𝑜𝑑 𝑝 = 𝑔𝑎𝑏 𝑚𝑜𝑑 𝑝 = (𝑔𝑎 𝑚𝑜𝑑 𝑝)𝑏 𝑚𝑜𝑑 𝑝 = 𝐴∗𝑏 𝑚𝑜𝑑 𝑝 (3.5) Формула (3.5) доказывает, что с помощью секретных ключей разных пользователей можно вычислить общий секретный ключ. В практических реализациях, для a и b используются числа порядка 10100 и p порядка 10300. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка. 3.6. Шифрование с помощью алгоритма Диффи-Хеллмана Главная проблема алгоритм заключается в том, чтобы зашифровать сообщение М, которое может быть представлено на ЭК в виде точки 𝑃𝑚 (𝑥,𝑦).[15] В шифровании и дешифровании сообщения, как и в случае передачи ключей по каналу связи, в качестве параметров выбирается эллиптическая кривая 𝐸𝑝 (𝑎,𝑏) и точка пораждающая точка G которая принадлежит данной кривой. Пользователь 1 выбирает закрытый ключ 𝑛𝐵 и вычисляет открытый ключ путем перемножения закрытого ключа на точку G. Чтобы зашифровать сообщение 𝑃𝑚 используется открытый ключ пользователя 2 (PB). Пользователь 1 выбирает случайное целое положительное число k и вычисляет зашифрованное сообщение 𝐶𝑚, являющееся точкой на эллиптической кривой. 𝐶𝑚 = (𝑘 × 𝐺,𝑃𝑚 + 𝑘 × 𝑃𝐵) (3.6) Для того, чтобы расшифровать сообщение (3.6), пользователь 2 умножает первую координату точки на свой закрытый ключ и получает результат из второй координаты по формуле (3.7): 𝑃𝑚 + 𝑘 × 𝑃𝐵 − 𝑛𝐵 × (𝑘 × 𝐺)=𝑃𝑚 + 𝑘 × (𝑛𝐵 × 𝐺)− 𝑛𝐵 × (𝑘 × 𝐺)= 𝑃𝑚 (3.7) Пользователь 1 зашифровал сообщение Pm добавлением к нему 𝑘∗𝑃𝐵. Никто не знает значения k, следовательно, хотя PB и является открытым ключом, никто не знает k × PB. Человеку, который пытается взломать алгоритм придется вычислить k, зная G и k × G. Эта операция довольно сложная. Получатель также не знает k, но ему в качестве подсказки посылается k × G. [16] Умножив k × G на свой закрытый ключ, получатель вычислит значение, которое было добавлено отправителем к исходному сообщению. [17] Тем самым получатель, не зная k, но имея свой закрытый ключ, может восстановить незашифрованное сообщение. [18] 4 ГЛАВА. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ Исследование эффективности выбранных криптографических алгоритмов в моей работе будет показано с помощью сбора временных показателей. В качестве сравнения будет рассмотрено время, которое необходимо для шифровки входного сообщения, время для дешифровки, а также, будет рассматриваться время, которое необходимо злоумышленнику для того чтобы взломать код, зная параметры кривой открытый ключ и зашифрованное сообщение. Выбранные данные представлены в виде таблиц для более удобного сравнения полученных данных. Исходя из этого, было решено создать приложение, которое может обрабатывать выбранные данные для кривых и анализировать время, потраченное для на обработку вычислений. В качестве среды разработки была выбрана Microsoft Visual Studio 2012, а в качестве языка программирования был выбран – Visual Basic. В программе было реализовано добавление новых эллиптических кривых в базу данных, для того чтобы пользователь мог выбрать параметры из предложенного списка. Данную базу данных можно изменять и расширять. В ходе реализации программного кода было принято решение брать текст для шифровки из текстового файла. Тем самым любой человек, который будет пользоваться данной программой может спокойно зашифровать любой текст. В программе были реализованы несколько функция для удобства вычислений. 4.1. Функция нахождения обратного элемента Function obratni (ByVal t As BigInteger) На вход данной функции подается число типа BigInteger В данной функции нахождение обратного элемента происходит по закону конечного поля. А именно обратным элементом конечного поля является такое число x при котором выполняется следующее равенство (4.1): 𝑋 ∗ 𝑇 𝑚𝑜𝑑 𝑝 = 1 (4.1) Где p – характеристика выбранного поля, T – элемент поля, которому необходимо найти обратный элемент Функция реализует этот алгоритм путем перебора всевозможных значений x пока не будет выполняться условие. С помощью команды return функция передает вычисленный обратный элемент в поле 4.2. Процедура удвоения точки на эллиптической кривой Sub udvoenie(ByVal x1 As BigInteger, ByVal y1 As BigInteger) На вход данной процедуры подаются числа типа BigInteger В этой процедуре происходит сложения точки с самой собой по формулам (1.7), (1.8), (1.6) представленных выше. Так как все вычисления происходят в конечном поле, то при вычислении формулы (1.7) необходимо будет воспользоваться функцией нахождения обратного элемента, о которой рассказывалось выше. При вычислении формулы (1.7) может произойти так, что число, полученное путем деления числителя на знаменатель будет не попадать в выбранное нами поле (например, оно может быть отрицательным). Для этого была создана проверка на принадлежность этого числа полю p. Если число оказывается меньше 0, то мы прибавляем к этому числу характеристику поля p до тех пор, пока оно не станет больше 0. Если же полученное число оказывается больше поля p, то мы просто вычисляем остаток от деления по модулю p. На выходе процедуры получаются координаты точки, полученные путем сложения выбранной точки с самой собой. 4.3. Процедура сложения точек на эллиптической кривой Sub slojenie(ByVal x1 As BigInteger, ByVal y1 As BigInteger, ByVal x2 As BigInteger, ByVal y2 As BigInteger) На вход данной процедуре пара точек. Сумма данных точек выполняется по формулам (1.4), (1.5), (1.6) по таким же законам что и в процедуре удвоения точки. На выходе процедуры получаются координаты точки, полученные путем сложения координат, которые в дальнейшем будут использоваться для новых преобразований. Полный текст программы приведен в Приложении. 4.4. Статистические данные В таблицах 4.1-4.10 представлены статистические данные временного анализа выбранных алгоритмов. Таблица 4.1 Временные данные для алгоритма Эль-Гамаля на эллиптических кривых для поля 1009
Таблица 4.2 Временные данные для алгоритма Диффи-Хеллмана на эллиптических кривых для поля 1009
Таблица 4.3 Временные данные для алгоритма Эль-Гамаля на эллиптических кривых для поля 3061
Таблица 4.4 Временные данные для алгоритма Диффи-Хеллмана на эллиптических кривых для поля 3061
Таблица 4.5 Временные данные для алгоритма Эль-Гамаля на эллиптических кривых для поля 31991
Таблица 4.6 Временные данные для алгоритма Диффи-Хеллмана на эллиптических кривых для поля 31991
Таблица 4.7 Временные данные для алгоритма Эль-Гамаля на эллиптических кривых для поля 426389
Таблица 4.8 Временные данные для алгоритма Диффи-Хеллмана на эллиптических кривых для поля 426389
Таблица 4.9 Временные данные для алгоритма Эль-Гамаля на эллиптических кривых для поля из стандарта NIST
Таблица 4.10 Временные данные для алгоритма Диффи-Хеллмана на эллиптических кривых для поля 426389
При анализе полученных данных из таблиц 4.1 – 4.10 можно заметить, что при выборе поля большого размера время, затраченное на атаку путем полного перебора, увеличивается. То есть криптостойкость алгоритмов растет с увеличением поля. Если была выбрана кривая над бинарным конечным полем как в таблице 4.7, 4.8, то можно заметить, что время кодирования и декодирования уменьшается, по сравнению с эллиптическими кривыми над полем простого числа. При этом были выбраны поля равные по длине. Так же можно заметить, что при выборе бинарного конечного поля криптостойкость алгоритма не сильно уменьшилась. Из этого можно сделать вывод, что при выборе поля одинаковой длинны, алгоритм, который использует бинарное конечное поле будет выполняться чуть быстрее. Выигрыш в скорости получается из-за того, что вычисления на компьютере происходят быстрее если числа, над которыми происходят операции могут быть представлены в виде степени двойки. Проанализировав графики 4.1, 4.2, 4.3, 4.4 можно заметить, что время, затраченное на вычисление открытого ключа, возрастает при выборе большего поля в обоих алгоритмах шифрования. Рисунок 4.1 Зависимость скорости вычисления открытого ключа от выбранного поля (Эль-Гамаль) 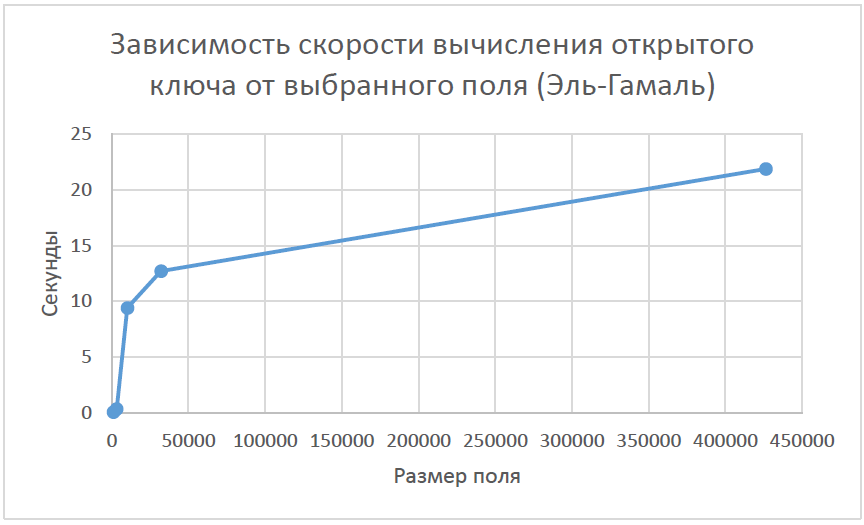 Рисунок 4.2 Зависимость скорости вычисления открытого ключа от выбранного поля (Диффи-Хеллман) 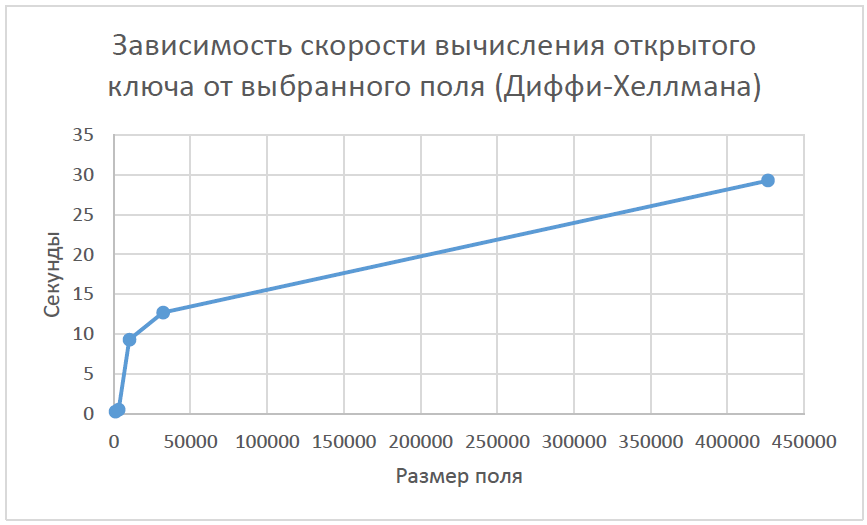 Рисунок 4.3 Зависимость скорости вычисления закрытого ключа от выбранного поля (Диффи-Хеллман) 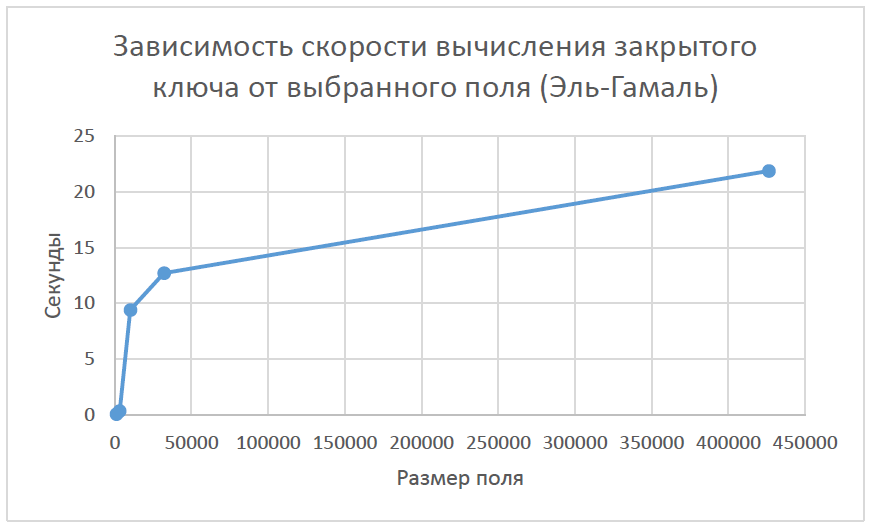 Рисунок 4.4 Зависимость скорости вычисления закрытого ключа от выбранного поля (Диффи-Хеллман) 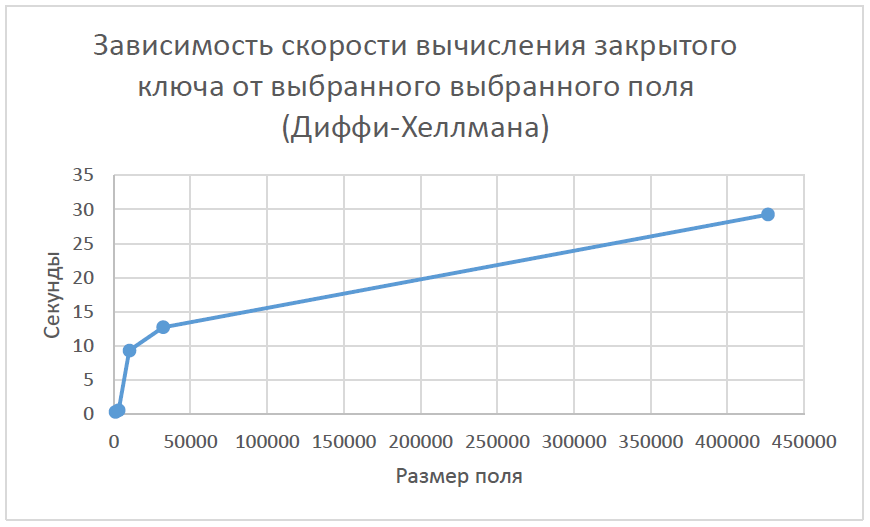 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
