Криптосистем основанные на эллиптических кривых. Содержание реферат
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
1.2. Проблематика современной криптографии В 70-ые годы прошлого века в современной криптографии произошел большой прорыв – впервые были созданы алгоритмы шифрования, которые не требовали передачи закрытых (секретных) ключей между пользователями по каналу связи. Такие алгоритмы были названы асимметричными алгоритмами шифрования. Первое упоминание об асимметричных шифрах было представлено в работе «Новые направления в современной криптографии» Уитфилда Диффи и Мартина Хеллмана, опубликованной в 1976 году. Изучая работы Ральфа Меркле о передаче открытого ключа, они разработали метод получения секретных ключей, по открытому каналу связи. Этот способ экспоненциального обмена ключами, который впоследствии стал называться обмен ключами Диффи-Хеллмана. Криптография - это наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонними) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации путем шифрования данных. Сама идея криптографии, использующая открытый ключ для шифрования данных, напрямую связана с односторонних функций [3], то есть существует такая функция f(x), что по известному x можно без труда найти значение f(x), тогда как определение x из f(x) достаточно непросто. Но использование односторонней функции в криптографии бесполезно, так как с помощью неё можно лишь зашифровать сообщение, но расшифровать нельзя. В этом случае ученые придумали алгоритм для достижения цели расшифровки данных. Они стали использовать односторонние функции с «секретом». Этот некий секрет способствует расшифровки текста. То есть существует некий y, что, зная f(x), можно вычислить x. В настоящее время в современной криптографии существуют ряд проблем: 1. Ограниченное количество рабочих моделей. Алгоритмы классической криптографии, могут быть созданы в большом количестве путем комбинирования различных методов элементарных преобразований. Каждая новая модель основывается на какой-либо "нерешаемой" задаче. В итоге количество функционирующих моделей криптографии с открытым ключом весьма невелико. 2. Постоянное увеличение размера передаваемых блоков данных и ключей, обусловленное инновациями в вычислительной техники и развитием математического аппарата[4]. Например, при создании криптосистемы RSA считалось, что достаточно взять размер чисел, не превышающих 512 бит, тогда как сейчас рекомендуется брать числа не менее 4 Кбит. Другими словами, размер чисел в криптосистеме RSA, которые можно использовать для безопасного кодирования вырос практически в 8 раз. Такая же картина наблюдается и для других моделей криптографии, тогда как в новой криптографии этот размер увеличился всего в 2 раза. 3. Потенциальная ненадежность базиса. Сейчас теорией вычислительной сложности рассматривается вопрос о решения задач данного типа за полиномиальное время. В рамках данной теории уже была доказана связь большинства используемых вычислительно сложных задач с другими аналогичными задачами. То есть, если будет взломана хотя бы одна современная криптосистема, то другие будут подвергнуты такой же опасности. 4. Отсутствие перспективы. Сейчас уже известно, что современная криптография находится под угрозой из-за квантовых вычислительных систем, с помощью которых можно решить задачи во много раз быстрее, чем на обычных компьютерах.[5] Ученые предполагают, что серьёзные квантовые компьютеры появятся в нашем мире примерно через 20-25 лет, и как следствие – будущее криптографии становится туманным. В итоге для современной криптографии стала актуальна задача повышения криптостойкости и уменьшения размера передаваемых блоков данных путем изменения уже существующих криптосистем. Необходимо было развивать новые направления в методах защиты информации. Выходом из этой ситуации стал относительно молодой раздел науки – эллиптическая криптография. Данный раздел науки изучает асимметричные криптосистемы, которые базируются на эллиптических кривых над конечными полями. 1.3. Эллиптическая криптография Самый явный путь решения проблемы повышения стойкости - представление шифруемых блоков информации в криптографических алгоритмах не только с помощью чисел, но и с помощью иных алгебраических элементов большей сложности. Самыми подходящим типами таких элементов являются точки эллиптических кривых. Эллиптические кривые считаются одними из наиболее перспективных объектов для изучения в современной теории чисел и криптографии. Криптографический протокол - это абстрактный или конкретный протокол, включающий набор криптографических алгоритмов. В основе протокола лежит набор правил, регламентирующих использование криптографических преобразований и алгоритмов в информационных процессах. Функции криптографических протоколов Аутентификация источника данных Аутентификация сторон Конфиденциальность данных Невозможность отказа Невозможность отказа с доказательством получения Невозможность отказа с доказательством источника Целостность данных Обеспечение целостности соединения без восстановления Обеспечение целостности соединения с восстановлением Разграничение доступа Классификация Протоколы шифрования и расшифрования. В основе протокола этого класса содержится некоторый симметричный или асимметричный алгоритм шифрования и расшифрования. Алгоритм шифрования выполняется на передаче отправителем сообщения, в результате чего сообщение преобразуется из открытой формы в шифрованную. Алгоритм расшифрования выполняется на приёме получателем, в результате чего сообщение преобразуется из шифрованной формы в открытую. Так обеспечивается свойство конфиденциальности. Для обеспечения свойства целостности передаваемых сообщений симметричные алгоритмы шифрования и расшифрования, обычно, совмещаются с алгоритмами вычисления имитозащитной вставки (ИЗВ) на передаче и проверки ИЗВ на приёме, для чего используется ключ шифрования. При использовании асимметричных алгоритмов шифрования и расшифрования свойство целостности обеспечивается отдельно путем вычисления электронной цифровой подписи (ЭЦП) на передаче и проверки ЭЦП на приёме, чем обеспечиваются также свойства безотказности и аутентичности принятого сообщения. Протоколы электронной цифровой подписи (ЭЦП). В основе протокола этого класса содержится некоторый алгоритм вычисления ЭЦП на передаче с помощью секретного ключа отправителя и проверки ЭЦП на приёме с помощью соответствующего открытого ключа, извлекаемого из открытого справочника, но защищенного от модификаций. В случае положительного результата проверки протокол, обычно, завершается операцией архивирования принятого сообщения, его ЭЦП и соответствующего открытого ключа. Операция архивирования может не выполняться, если ЭЦП используется только для обеспечения свойств целостности и аутентичности принятого сообщения, но не безотказности. В этом случае, после проверки, ЭЦП может быть уничтожена сразу или по прошествии ограниченного промежутка времени ожидания. Протоколы идентификации и аутентификации. В основе протокола идентификации содержится некоторый алгоритм проверки того факта, что идентифицируемый объект (пользователь, устройство, процесс, и т.д.), предъявивший некоторое имя (идентификатор), знает секретную информацию, известную только заявленному объекту, причем метод проверки является, конечно, косвенным, то есть без предъявления этой секретной информации. Обычно с каждым именем (идентификатором) объекта связывается перечень его прав и полномочий в системе, записанный в защищенной базе данных. В этом случае протокол идентификации может быть расширен до протокола аутентификации, в котором идентифицированный объект проверяется на правомочность заказываемой услуги. Если в протоколе идентификации используется ЭЦП, то роль секретной информации играет секретный ключ ЭЦП, а проверка ЭЦП осуществляется с помощью открытого ключа ЭЦП, знание которого не позволяет определить соответствующий секретный ключ, но позволяет убедиться в том, что он известен автору ЭЦП. Протоколы аутентифицированного распределения ключей. Протоколы этого класса совмещают аутентификацию пользователей с протоколом генерации и распределения ключей по каналу связи. Протокол имеет двух или трёх участников; третьим участником является центр генерации и распределения ключей (ЦГРК), называемый для краткости сервером S. Протокол состоит из трёх этапов, имеющих названия: генерация, регистрация и коммуникация. На этапе генерации сервер S генерирует числовые значения параметров системы, в том числе, свой секретный и открытый ключ. На этапе регистрации сервер S идентифицирует пользователей по документам (при личной явке или через уполномоченных лиц), для каждого объекта генерирует ключевую или идентификационную информацию и формирует маркер безопасности, содержащий необходимые системные константы и открытый ключ сервера S (при необходимости). На этапе коммуникации реализуется собственно протокол аутентифицированного ключевого обмена, который завершается формированием общего сеансового ключа. Задачи Обеспечение различных режимов аутентификации Генерация, распределение и согласование криптографических ключей Защита взаимодействий участников Разделение ответственности между участниками Разновидности атак на протоколы Атаки, направленные против криптографических алгоритмов Атаки против криптографических методов, применяемых для реализации протоколов Атаки против самих протоколов (активные или пассивные) Требования к безопасности протокола Аутентификация (нешироковещательная): аутентификация субъекта аутентификация сообщения защита от повтора Аутентификация при рассылке по многим адресам или при подключении к службе подписки/уведомления: неявная (скрытая) аутентификация получателя аутентификация источника Авторизация (доверенной третьей стороной) Свойства совместной генерации ключа: аутентификация ключа подтверждение правильности ключа защищенность от чтения назад формирование новых ключей защищенная возможность договориться о параметрах безопасности Конфиденциальность Анонимность: защита идентификаторов от прослушивания (несвязываемость) защита идентификаторов от других участников Ограниченная защищенность от атак типа «отказ в обслуживании» Инвариантность отправителя Невозможность отказа от ранее совершенных действий: подотчетность доказательство источника доказательство получателя Безопасное временное свойство 1.4. Математика эллиптической кривой и конечных полей Эллиптической кривой E называют множество пар точек (x, y), удовлетворяющих уравнению (1.1): 𝑦2+𝑎1𝑥𝑦+𝑎3𝑦=𝑥3+𝑎2𝑥2+𝑎4𝑥+𝑎6 (1.1) Варианты графиков эллиптических кривых приведены на рисунке 1.2. Рисунок 1.2 Графики эллиптических кривых 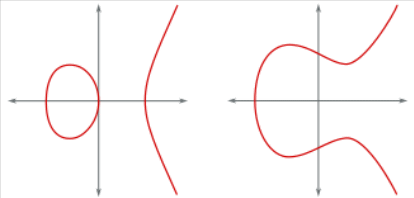 В большинстве случаев в криптографии основанных на эллиптических кривых рассматриваются 2 вида кривых над конечными полями: 1. простыми полями нечётной характеристики (Zp, где p > 3 и является простым числом) 2. полями характеристики 2 (GF(2m)). В полях характеристики 2 обычно рассматриваются два вида эллиптических кривых (1.2) и (1.3): 1. Суперсингулярная кривая 𝑦2 + 𝑎𝑦 = 𝑥3 + 𝑏𝑥 + 𝑐 (1.2) 2. Несуперсингулярная кривая 𝑦2 + 𝑎𝑥𝑦 = 𝑥3 + 𝑏𝑥2 + 𝑐 (1.3) Но далеко не все эллиптические кривые подходят для реализации в эллиптической криптографии. Эллиптическая кривая E(Fp) над конечным простым полем Fp, где p – является порядком поля, которое должно быть больше 3, может быть отображена с помощью модифицированного уравнения, также называемым «каноническим», в форме Вейерштрасса, которая вычисляется по формуле (1.4): 𝑦2=𝑥3+𝑎𝑥+𝑏 (𝑚𝑜𝑑 𝑝) (1.4) где a и b принадлежат полю Fp и дискриминант 4𝑎3+27𝑏2 не должен равняться 0 по модулю p. Если это неравенство не может быть выполнено, то кривые считаются сингулярными. В математике сингулярностью обозначается такая точка, в которой предложенная функция имеет странное поведение, например, стремится к бесконечности. Ученые считают, что использование сингулярных кривых в алгоритмах криптографии приводят к уменьшению криптостойкости алгоритма. Поэтому использование таких кривых запрещено. Рисунок 1.3. Пространственный график эллиптической кривой 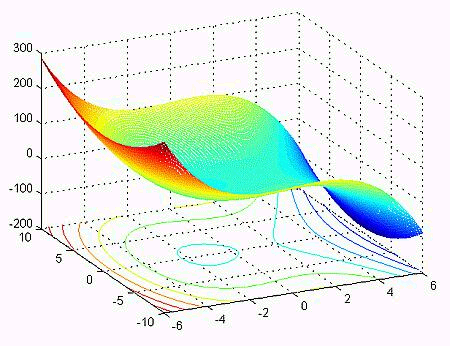 Все арифметические вычисления в эллиптической криптографии проходят не над выбранной кривой, а только над точками, которые принадлежат этой кривой, которые в свою очередь образуют определенную группу. Над точками кривой могут быть выполнены следующие три основные операции: 1. сложение двух разных точек 2. удвоение точки 3. умножение точки на число Основной операцией является операция сложения, так как именно на ней основываются все дальнейшие операции. 1.4.1. Сложение точек на эллиптической кривой Сложение двух точек эллиптической кривой заключается в том, что если взять две точки P и Q, которые лежат на данной кривой, и провести через них прямую, то эллиптическая кривая будет иметь пересечение этой прямой в третьей точке. Так как эллиптическая кривая будет симметричной относительно оси Х, то мы можем зеркально отразить эту точку относительно оси X, получив новую точку P+Q принадлежащую данной кривой (Рис. 1.4). Рисунок 1.4 Сложение точек на эллиптической кривой 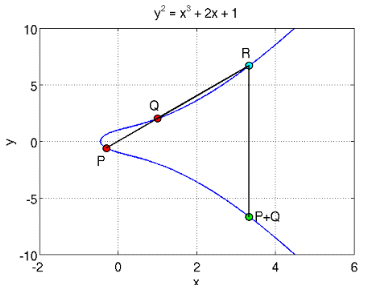 Пусть дана кривая 𝑦2=𝑥3+𝑎𝑥+𝑏 (1.5) над полем k (𝑘≠2 и 𝑘≠3), и точки P=(𝑥𝑝, 𝑦𝑝) и Q=(𝑥𝑞, 𝑥𝑞) принадлежащие кривой (1.5) Предположим, что 𝑥𝑝≠𝑥𝑞. Пусть формула нахождения углового коэффициент секущей 𝑆=𝑦𝑝−𝑦𝑞𝑥𝑝−𝑥𝑞 (𝑚𝑜𝑑 𝑘) (1.6) так как k — поле, то s строго определено. Тогда мы можем определить 𝑅=𝑃+𝑄=(𝑥𝑟,𝑦𝑟) следующим образом: 𝑥𝑟 =𝑠2 − 𝑥𝑝−𝑥𝑞 (𝑚𝑜𝑑 𝑘) (1.7) 𝑦𝑟 =𝑠(𝑥𝑃− 𝑥𝑅)−𝑦𝑝 (𝑚𝑜𝑑 𝑘) (1.8) Формулы сложения (1.7) и (1.8) показывают, что координаты суммы двух точек выражаются через координаты слагаемых рационально, следовательно, если координаты выбранных точек принадлежат выбранному полю, то и сумма этих точек принадлежит этому же полю. [8] 1.4.2. Удвоение точек на эллиптической кривой Удвоение точки эллиптической кривой происходит немного по-другому, нежели сложение двух точек. Основное отличие заключается в нахождении углового коэффициент секущей, проведенной через точку. Он высчитывается по формуле (1.9) 𝑆=3𝑥𝑝+𝑎2𝑦𝑝 (𝑚𝑜𝑑 𝑘) (1.9) Вычисление же координат остается неизменным, они вычисляются по формулам (1.7) и (1.8). 1.4.3. Оценка числа элементов группы точек эллиптической кривой Данные свойства позволяет говорить о конечной группе точек в котором можно строить криптографические алгоритмы. Для выбранной эллиптической кривой количество точек в группе конечно. Данное количество точек в группе эллиптической кривой m можно определить по формуле (1.10): 𝑝+1−2√𝑝≤𝑚≤𝑝+1+2√𝑝 (1.10) где р – порядок поля, над которым определена кривая. 1.5. Выбор набора параметров для эллиптической кривой Для использования эллиптической кривой в алгоритмах шифрования все пользователи должны согласовать все параметры, которые определяют эллиптическую кривую. Эллиптическая кривая определяется константами a и b из уравнения (2). Абелева подгруппа точек задается одной порождающей точкой G. Следовательно, для выбранного конечного поля 𝑍𝑝, где p > 3, набор параметров для шифрования должен быть таковым: (p,a,b,G). В США были вычислены рекомендованные наборы параметров для использования эллиптических кривых в криптографических алгоритмах. Данные параметры были представлены в стандартах NIST Для создания собственного набора параметров необходимо: 1. Выбрать набор параметров. 2. Определить эллиптическую кривую, которая будет удовлетворять выбранным условиям. Для нахождения кривой для заданного набора параметров используются два метода: 1. Выбрать случайную кривую, и использовать алгоритмом подсчета точек 2. Выбрать точки и построить по ним кривую, используя технологию умножения. Существует несколько классов эллиптических кривых, которые не стоит использовать в алгоритмах шифрования из-за их слабостей к некоторым видам атак. Например, кривые над полем 𝐹2𝑚, где m - не простое число. Выбирая такие кривые алгоритмы могут быть подвержены атакам Вейля. При выборе определенных параметров можно добиться ускорения работы алгоритма. Так, например, деление по модулю p могут выполняться гораздо быстрее на персональных компьютерах, если характеристикой поля взять простое числа Мерсенна которые высчитываются по формуле 𝑀𝑛=2𝑛−1. Большинство таких кривых и представлены в рекомендуемых параметрах NIST Если в качестве коэффициента a взять число a = − 3, то при реализации алгоритма будет выигрыш в скорости при сложении точек на эллиптической кривой. |
