проект. Моделирование электрических полей. Содержание введение 3 глава основы теории и вопросы моделирования

• Название: Содержание введение 3 глава основы теории и вопросы моделирования
• Анкор: проект
• Дата: 25.05.2023
• Размер: 1.02 Mb.
• Имя файла: Моделирование электрических полей.docx
• Тип: Реферат; #1158642
• страница: 6 из 12

1.5. Потенциал

Напряженность Е является силовой характеристикой электрического поля, т.к. определяет силу, действующую на электрический заряд, находящийся в поле E. Однако часто легче исследовать свойства системы, рассматривая энергии, а не силы. С этой целью в электромагнетизме вводится понятие электрического потенциала V(r), определяемого соотношением:

𝑝₁
или

^{𝑉(𝑟2) − 𝑉(𝑟1) = −} ∫^{𝑝2 𝐸𝑑𝑟}

(1.16)

𝐄⁽𝐫⁾ = −∇𝑉(𝐫). (1.17)
Электрический потенциал V(r) является скалярной величиной, и физический смысл имеет только разность потенциалов в двух точках. Дифференциальный оператор ≡ gradв декартовых координатах имеет вид:

∇= ^𝜕

𝜕𝑥

𝐢 + ^𝜕

𝜕𝑦

𝐣 + ^𝜕

𝜕𝑧

𝐤, (1.18)

где i, j, k − единичные векторы (орты) соответственно осей x, y, z. В одномер- ном случае формула сводится к E(x) = − dV/ dx, а если потенциал V зависит только от модуля r(сферическая симметрия), то E(r)= − dV/ dr.

Во всех случаях направление вектора Е совпадает с направлением наибо- лее быстрого убывания потенциала, что является общим свойством поля Е.

Потенциал точечного заряда (при условии, что на бесконечности он равен нулю) легко получить, проинтегрировав правую часть в формуле, где Е опреде- ляется законом Кулона:
V⁽r⁾ = ^q . (1.19)

4π𝗌₀r
Поверхность, на которой потенциал принимает одинаковые значения, называется эквипотенциальной поверхностью, которая везде ортогональна си ловым линиям электрического поля. В двумерном случае − это эквипотенци альные линии.

Используя свойство ортогональности эквипотенциальных линий силовым линиям электрического поля можно теперь нарисовать в двумерном случае эквипотенциальные линии. Действительно, если компоненты силовой линии определяются формулами (1.16), то компоненты отрезка, перпендикулярного Е, будут определяться следующими формулами [1]:

∆x = −∆s ^Ey , ∆y = ∆s ^Ex. (1.20)

^|𝐄^{| |}𝐄^|
Таким образом, мы теперь можем, используя тот же алгоритм, что был рассмотрен выше для рисования силовых линий электрического поля, рисовать также эквипотенциальные линии, т.е. моделировать электрическое полеEдля стационарного распределения зарядов.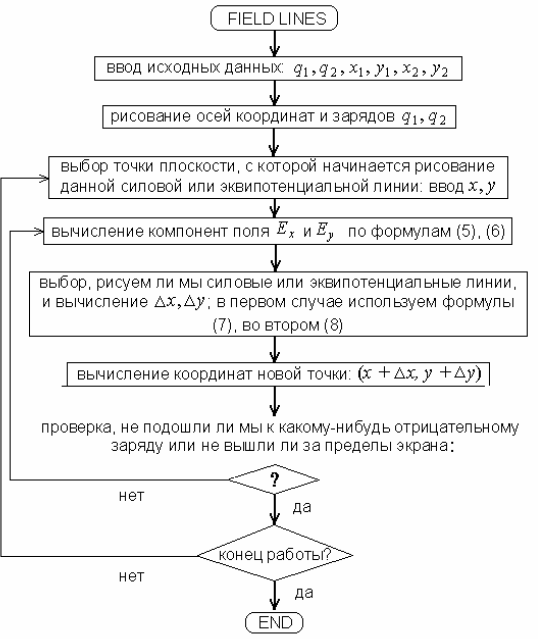

Общая блок-схема алгоритма, реализующего метод, будет выглядеть, как пока- зано на рис. 1.8.
Рис.1.8. Блок-схема алгоритма