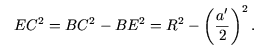Курсовая работа Дианы. Содержание Введение Индукция в геометрии теоретические аспекты Практическое применение темы индукция в геометрии заключение Список использованных источников введение
 Скачать 5.98 Mb. Скачать 5.98 Mb.
|
|
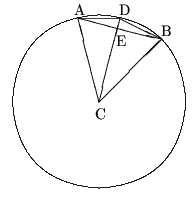
Теорема 6.n-член геометрической прогрессии может быть вычислен по формуле Доказательство: Пусть n = 1. Тогда получаем верное тождество: b1 = b1. Пусть данная формула верна для n = k: Докажем эту формулу для n = k + 1, т. е. необходимо доказать, что Теорема 7.Сумму nчленов геометрической прогрессии можно найти по формуле Доказательство: Пусть n = 1. Тогда Предположим, что формула имеет место для n = k. Тогда докажем, что Докажем методом математической индукции теоремы, связанные с нахождением числа размещений, перестановок, сочетаний [3]. Определение 20. Размещением из nэлементов по kэлементам называется упорядоченное подмножество данного n множества, содержащее kэлементов. Число всех возможных размещений из nэлементов по kэлементам обозначается Определение 21. Факториал числа n – это произведение всех натуральных чисел от 1 до nвключительно, т. е. Теорема 8. Число всех возможных размещений из nэлементов по kэлементам можно вычислить по формуле Доказательство: Докажем данную теорему индукцией по k. Несложно заметить, что Предположим, что Замечание 5. Также число всех возможных размещений из nэлементов по kэлементам можно вычислить по формуле Определение 22. Перестановкой из n элементов называется размещение из nэлементов по n элементам. Число всех возможных перестановок из n элементов обозначается Pn. Теорема 9. Число всех возможных перестановок из n можно вычислить по формуле Pn = n! Доказательство: Несложно заметить, что P1 = 1, а значит для n = 1 формула верна. Пусть данная формула верна при n = k. Тогда докажем, что Pk+1 = (k + 1)! Из данных k + 1 элементов a1, a2, …, ak, ak+1возьмём только первые kэлементов и составим из них все возможные перестановки. По предположению индукции таких перестановок будет k! В каждой из этих перестановок поставим элемент ak+1последовательно перед 1-м элементом, потом перед 2-м элементом, …, перед k-м элементом, после k-ого элемента. Этим путём мы из одной перестановки из kэлементов получим k + 1 перестановок из k + 1 элементов. Тогда всего имеем: Pk+1 =k!(k + 1) = (k + 1)! Замечание 6. В целом, для доказательства теоремы 9 можно было воспользоваться определением 22: Pn = Определение 23. Сочетанием из n элементов по k элементам называется подмножество данного nмножества, содержащее k элементов. Число всех возможных сочетаний из n элементов по k элементам обозначается Теорема 10. Число всех возможных сочетаний из n элементов по k элементам Доказательство: Пусть k = 1. Для продолжения доказательства произведём тождественные преобразования над данной формулой. Замечание 7. На практике для нахождения числа всех возможных сочетаний из n элементов по k элементам удобно пользоваться формулой Теорема 11 (Бином Ньютона). 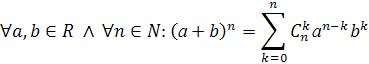 Доказательство: Так как любое число, отличное от нуля, в нулевой степени равно 1, то (a + b)0 = 1 = Пусть 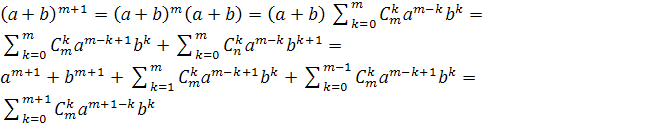 Что и требовалось доказать. Что и требовалось доказать.2. Практическое применение темы « индукция в геометрии» 2.1 Вычисление по индукции Задача №1. Вычислить сторону Решение: n = 2, правильный 22-угольник есть квадрат, и в этом случае a4 = R
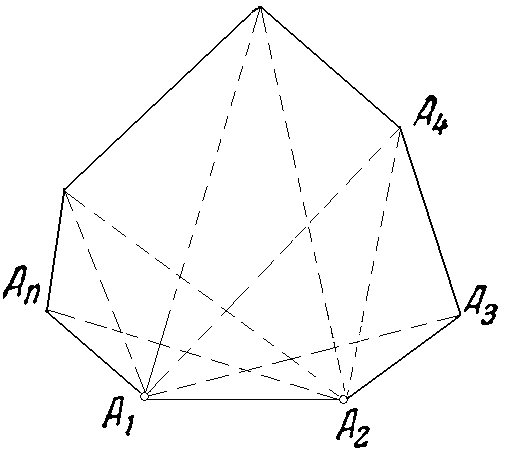
Таким образом, 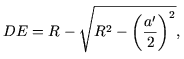 и, следовательно, и, следовательно, 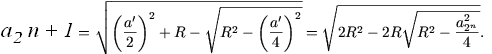 формула перехода от n к n + 1. В частных случаях 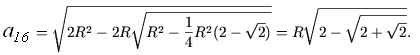 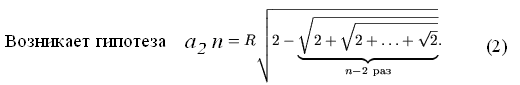 Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим Согласно формуле перехода, 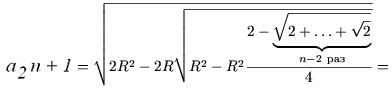 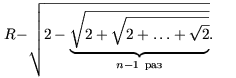 Из (2) следует, что длина окружности равна 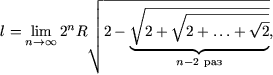 и, поскольку l = 2R, получим 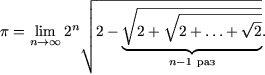 Задача № 2. Указать правило вычисления числа Р(п) способов, которыми выпуклый n-угольник может быть разбит на треугольники непересекающимися диагоналями. Решение: 1. Для треугольника это число равно, очевидно, единице: Р (3)=1. 2. Предположим, что мы уже определили числа Р(к) для всех к<п; найдем, чему равно в таком случае Р(п). Для этого рассмотрим выпуклый п-угольннк А1 А2 …Аn (рисунок 2). При всяком разбиении его на треугольники сторона А1 А2 будет стороной одного из треугольников разбиения, третьи вершина этого треугольника может совпасть с каждой из точек A1 A 3 A4 Число способов разбиения n-угольника,при которых эта вершина совпадает с точкой A3, равно числу способов разбиения на треугольники(п—1)-угольника A1 A3 A4…An , т. е. равно Р(п—1).
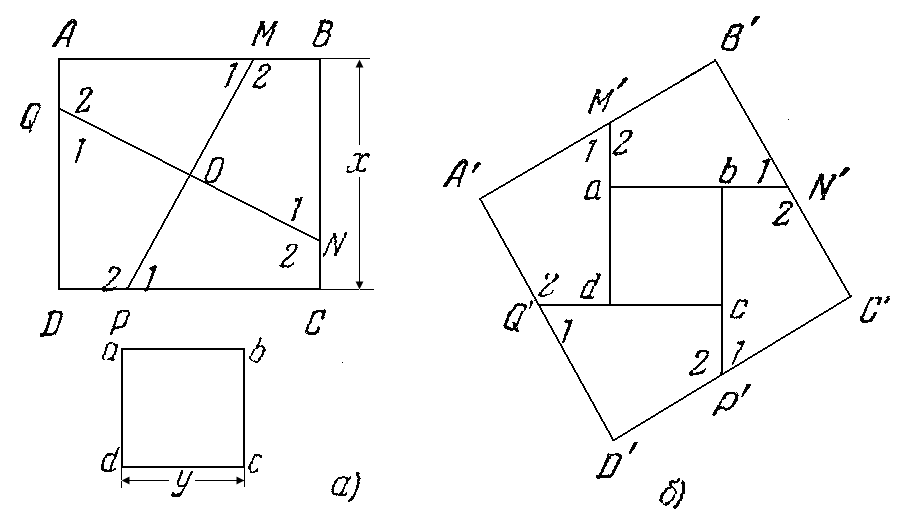
каждым из разбиений четырехугольника A2 A3 A4 A5 , и т. д. Таким образом, мы приходим к следующему соотношению: Р(п) = Р(п— 1) + Р (n —2) Р (3) + Я (n— 3) Р(4)+ … ...+P(3)Р(n — 2) + Р(n —1). (7) С помощью этой формулы последовательно получаем: P (4)= P (3)4+P (3)=2, P(5) = Р(4) + P(3)Р(3)4+P(4) = 5, Р(6)=Р(5)+Р(4)Р(3)+P(3)Р(4)+P(5)=14, P (7) = Р(6)+Р (5) Р (3) + Р (4) Р (4)+Р(3)Р (5) + Р(6)=42, P(8)=P(7)+P(6)P(3) + P(5)P(4) + P(4)P(5) + +P(3)Р(6)+Р(7)=132 и т. д. С помощью формулы (7) можно доказать, что при всяком п Наиболее естественное применение метода математической индукции в геометрии, близкое к использованию этого метода в теории чисел и в алгебре - это применение к решению геометрических задач на вычисление [5]. Задача на вычисление - это задача, в которой требуется выразить неизвестные величины (отрезки, углы, площади и др.) или их отношения через известные величины, которые могут быть даны в общем виде или числовыми значениями. 2.2 Доказательство по индукции Задача № 3. Дано п произвольных квадратов. Доказать, что их можно разрезать на части так, что из полученных частей можно сложить новый квадрат. Решение: 1° При п=1 наше утверждение не нуждается в доказательстве. Докажем, что и при п =2 оно также справедливо. Обозначим стороны заданных квадратов ABCD и abcd соответственно через х и у; пусть На сторонах квадрата ABCD со стороной х (рисунок 3, а) отложим отрезки AM=BN = CP = DQ = Эти куски приложим ко второму квадрату, как показано на рисунке 3 , б.
Выберем любые два из этих квадратов, скажем Кnи Kn+1. Как показано в п. 1°, разрезая один из этих квадратов и прикладывая полученные куски ко второму, можно получить новый квадрат К'. Далее, согласно сделанному нами предположению квадраты K1, K2,.., Кn-1, К' можно так разрезать: на части, что из этих частейможно сложить новый квадрат. Что и требовалось доказать. Задача № 4. Доказать, что сумма первых n (n Решение: Так как утверждение зависит от натурального параметра n, то воспользуемся для его доказательства методом математической индукции. 1) Проверим справедливость данного утверждения для n = 1, если n = 1, то 1 = 12; 2) предположим, что сумма первых k (k 3) установим, исходя из равенства (2), что сумма первых k +1 нечетных чисел равна 1 + 3 + 5 +…+ (2(k + 1) – 1) = 1 + 3 + 5 +…+ (2(л + 1) – 1) = 1 + 3 + 5 +… (2л + 1) = 1 + 3 + 5 +…+ (2л –1) + (2л + 1) = х1 + 3 + 5 +…+ (2л – 1)ъ + (2л + 1) = На основании принципа математической индукции делаем вывод, что сумма первых n нечетных чисел равна n2 для любого натурального n. |