Курсовая работа Дианы. Содержание Введение Индукция в геометрии теоретические аспекты Практическое применение темы индукция в геометрии заключение Список использованных источников введение
 Скачать 5.98 Mb. Скачать 5.98 Mb.
|
|
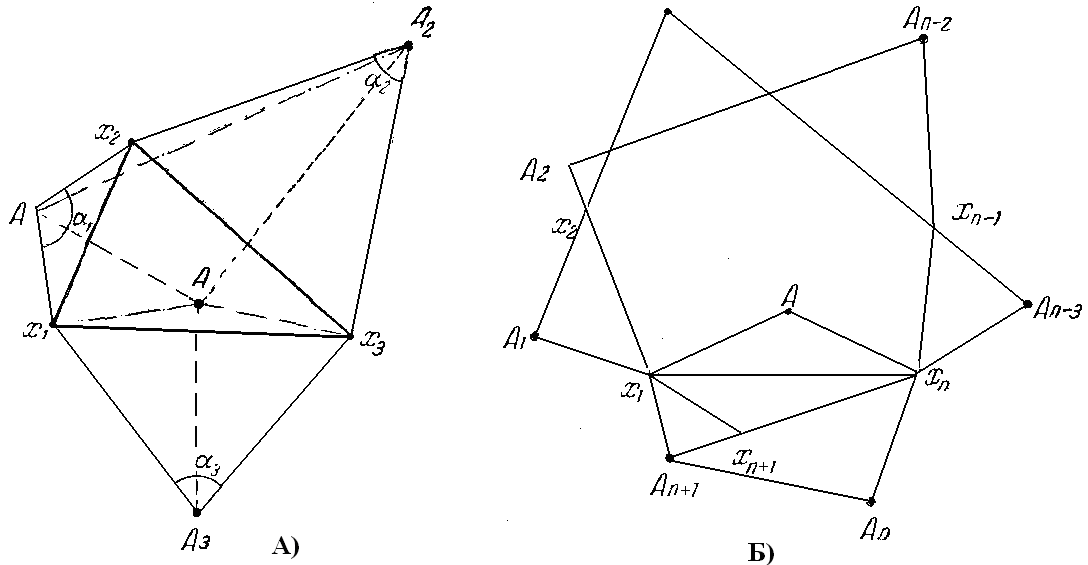
Задача №5. Доказать, что для n-го члена геометрической прогрессии { Решение: Доказательство проводим методом математической индукции по натуральному параметру n. 1) 2) Предположим, что формула справедлива для всех натуральных значений n от 2 до k включительно, т. е. 3) Согласно принципу математической индукции, можно сказать, что рассматриваемая формула верна для любого натурального n. Задача №6. Доказать, что при каждом натуральном n число Решение: Обозначим число 1) 2) 3) Если мы сумеем доказать, что Это доказательство проведем также методом математической индукции: 3) Тогда Итак, Согласно методу математической индукции, мы можем сказать, что число Задача №7. Доказать, что при каждом натуральном n справедлива формула 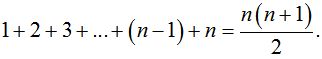 Решение: 1)  ; 1 = 1(истина); ; 1 = 1(истина);2) 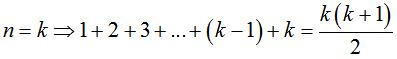 (предположение). (предположение).3) 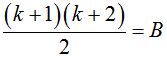 . .Чтобы доказать, что А = В, мы можем: с помощью тождественных преобразований перевести А в В; с помощью тождественных преобразований перевести В в А; с помощью тождественных преобразований перевести А в С; с помощью тождественных преобразований перевести В в С; Воспользуемся приемом (3) 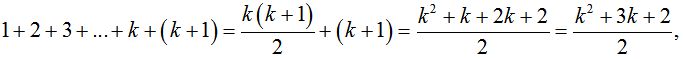 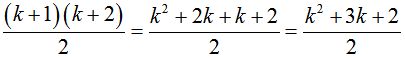 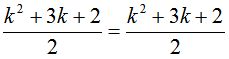 . .Согласно принципу математической индукции, делаем вывод: 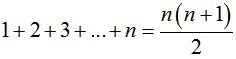 при при Таким образом, доказательство - предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального n. Тогда существует такое натуральное m, что: 1) утверждение для n=m несправедливо, 2) для всякого n, меньшего m, утверждение справедливо (иными словами, m есть первое натуральное число, для которого утверждение несправедливо). Очевидно, что m>1, т.к. для n=1 утверждение справедливо (условие 1). Следовательно, Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число [8]. Доказательство, основанное на принципе математической индукции, называется методом полной математической индукции. 2.3 Построение по индукции Задача №8. На плоскости даны п точек. Построить n-угольник, стороны которого являются основаниями равнобедренных треугольников с вершинами в данных п точках и углами Решение: Мы будем считать, что некоторые из углов 1° Пусть n = 3. Допустим, что задача решена, x1,x2,x3— вершины искомого треугольника, A1,A2,A3— заданные вершины построенных на его сторонах равнобедренных треугольников с углами При повороте плоскости вокруг точки А1на угол Оба эти поворота, последовательно выполненные один за другим, равносильны одному повороту на угол При этом результирующем повороте вершина х1переходит в x3. Следовательно, вершина х3переходит в х1при повороте вокруг точки А на угол 360° - По точкам А и A3, если они не совпадают (что может иметь место, лишь если Точки пересечения сторон этих углов и будут вершинами х1и х3искомого треугольника. После этого нетрудно построить и вершину x2. При
Рисунок 4 2° Предположим, что мы умеем строить n-угольник по вершинам построенных на его сторонах равнобедренных треугольников с заданными углами при вершинах, и пусть требуется построить. (n-1)-угольник по вершинам A1,A2,…, An,An+1 построенных на его сторонах равнобедренных треугольников с углами Пусть х1 х2. . . х1 хnxn+1 - искомый (п+1)-угольник (рисунок 4 б), Рассмотрим треугольник х1 хnxn+1. Как в п. 1°, по известным вершинам Аnи Аn+1равнобедренных треугольников хnАnхn+1и хn+1Аn+1х1, построенных на сторонах xnхn+1и xn+1x1,можно найти вершину А равнобедренного треугольника х1 Ахn, построенного на диагонали х1 хnи имеющего угол при вершине, равный 360°— ( Этим наша задача сводится к задаче о построении n-угольника x1 x2…xnпо вершинам А1 А2... Аn-1 А построенных на его сторонах равнобедренных треугольников с известными углами В силу индуктивного предположения n-угольник х1 х2, ... , хnможет быть построен, после чего уже нетрудно построить и искомый (n+1)-угольник x1x2…xnxn+1. При Таким образом, применение метода математической индукции к решению задач на построение может иметь место в том случае ... условии задачи фигурирует некоторое целое положительное число п (например, в задачах на построение n-угольников) [10]. Заключение В теоретической части курсовой работы, для изложения сути метода математической индукции и её доказательств нами были введены некоторые определения, обозначения и понятия из математической логики и теории множеств. Приведены теоремы и доказательства к ним. В практической части курсовой работы нами были рассмотрены примеры решения задач по следующим темам: вычисление по индукции, доказательство по индукции и построение по индукции. Важно - уметь размышлять индуктивно. Очевидно, что применение метода математической индукции очень широко в разных разделах математики школьного курса . В частности, его применяют: 1) в задачах на суммирование и для доказательства тождеств; 2) к доказательству неравенств; 3) к задачам на делимость; 4) для изучения свойств числовых последовательностей; 5) в геометрии : для вычисления по индукции ; для доказательства по индукции ; для построения по индукции ; для нахождения геометрических мест по индукции ; для определения по индукции ; для индукции по числу измерений. Метод математической индукции обучает искусству делать индуктивные предположения и является одним из методов решения олимпиадных задач. Приобретение опыта решения задач с использованием метода математической индукции помогает повысить уровень логической культуры. Список использованных источников Виленкин Н.Я. Индукция. Комбинаторика. Пособие для учителей. М., Изд-во Просвещение, 1976. 48 с. Головина Л.И., Яглом ИМ. Индукция в геометрии. - М.: Наука, 1961. 120 с. (Популярные лекции по математике.) Генкин Л. О математической индукции. / под ред. Яглома И.М.. – М.: Физмат-лит., 1962. 36 с. (серия «Математическая библиотека). Рубанов И.С. Как обучать методу математической индукции/ Математика школе. - № l. 1996. С.14-20. Соломинский И.С., Головина Л.И., Яглом И.М. О математической индукции. - М.:Наука. - 1967. С.7-59. Соминский И.С. Метод математической индукции. – М.: Наука, 1965 – 56 с. с ил. (Серия «Популярные лекции по математике»). Шень А. Математическая индукция. – М.: МЦНМО, 2004. 36 с. Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х. Пособие по математике для поступающих в вузы. / Под редакцией Г.Н. Яковлева. – М.: Гл. ред. «Физ.-мат. лит.», 1982. 480 с. «Математика. Алгебра. Начало математического анализа. Профильный уровень: учебник для 10 класса». / Шабунин М.И., Прокофьев А.А. – М.: БИНОМ. Лаборатория знаний. 2007. 424 с. «Математика. Алгебра. Начало математического анализа. Профильный уровень: задачник для 10 и 11 классов. / М.И. Шабунин, А.А. Прокофьев, Т.А. Олейник, Т.В. Соколова. – М. : БИНОМ. Лаборатория знаний. 2009. 477 с. |