Планирование эксперимента. Реферат ТЭ. Содержание Введение Планирование эксперимента Ортогональное планирование второго порядка Список литературы Введение
 Скачать 245.73 Kb.
|
 Содержание Введение……………………………………………………………………3 Планирование эксперимента……………………………………………...4 Ортогональное планирование второго порядка…………………………7 Список литературы……………………………………………………….13  Введение Развитие современной науки и техники связано с созданием новых и постоянным совершенствованием существующих научных и технологических процессов. Основой их разработки и оптимизации является эксперимент. Заметное повышение эффективности экспериментальных исследований и инженерных разработок достигается использованием математических методов планирования экспериментов. В процессе экспериментирования и при обработке полученных данных существенно сокращает сроки решения, снижает затраты на исследования и повышает качество полученных результатов. Цель планирования эксперимента – нахождение таких условий и правил проведения опытов при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности. Планирование экспериментаЧто такое планирование эксперимента  ?Целью планирования эксперимента является создание таких планов покачивания входных переменных, которые обеспечивают более быстрое и точное построение модели объекта (рис. 3.1.1). Выход объекта y состоит из неизвестного сигнала (функции  от входов) и центрированной помехи (M (h) = 0).  Функцию часто называют функцией (или поверхностью) отклика, а входные переменные  – факторами. Если мы имеем дело с малоизученным объектом, то вид функции 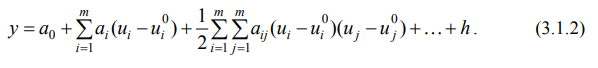неизвестен и удобным представлением ее является степенной ряд Тейлора в некоторой базовой точке   Здесь 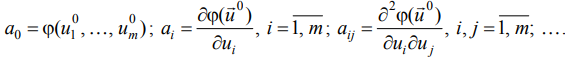 Модель объекта строим также в виде отрезка степенного ряда 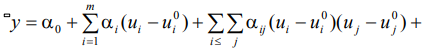  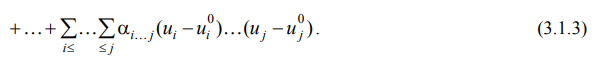Это уравнение называется уравнением регрессии. В нем (в отличие от ряда (3.1.2) исключены зависимые переменные, такие, например,  , а коэффициенты 1/ 2 и др. включены в параметры a. Уравнение регрессии отражает среднюю связь выхода объекта со входами. Параметры модели вычисляются обычно по методу наименьших квадратов на основе экспериментов  , полученных в результате реализации одного из планов, например, ортогональных.  С помощью планирования эксперимента решаются не только задачи построения модели объекта. Примером служит задача о взвешивании телВзвешивание трех тел (A, B, C) можно провести по традиционной схеме, приведенной в табл. 3.1.1. В ней "+" означает, что тело положено на весы, "–" указывает на отсутствие тела на весах. Вначале проводится "холостое" взвешивание и тем самым определяется "нулевая" точка весов. Затем по очереди взвешивается каждое из тел. Вес каждого тела оценивается по результатам двух опытов:  Если измерения независимые и равноточные, то дисперсия результатов взвешивания тел запишется в виде  где  – дисперсия ошибки взвешивания. Проведем теперь взвешивание по иной схеме, представленной в табл. 3.1.2. Вес каждого тела определяется по формулам:  В числителе стоят элементы последнего столбца со знаками, указанными в соответствующих столбцах A, B, C . Мы видим, что при вычислении, скажем, веса объекта A он входит в числитель два раза, и поэтому в знаменателе стоит число 2. Вес объекта A, вычисленный по приведенной выше формуле, оказывается неискаженным весами объектов B и C , так как вес каждого из них входит в формулу для веса объекта A дважды и с разными знаками. Найдем дисперсию, связанную с ошибкой взвешивания при новой схеме постановки эксперимента: 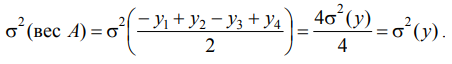 Аналогичным способом находим:  Видно, что при новой схеме взвешивания дисперсия веса объектов получается вдвое меньше, чем при традиционном методе взвешивания, хотя в обоих случаях выполнялось по четыре опыта. Увеличение точности эксперимента в два раза происходит по той причине, что в первом случае эксперимент был поставлен так, что каждый вес мы получали лишь по результатам двух опытов. Ортогональный план второго порядкаОртогональным планом называется такой план, у которого матрица планирования Х строится так, что бы матрица С= Хt Х оказалась диагональной. Используем этот подход и при построении планов второго порядка. План называется центральным, если все точки расположены симметрично относительно центра плана. ОЦКП – центральный симметричный ортогональный композиционный план. В ОЦКП входят: ядро - план ПФЭ с N0= 2nточками плана,n0(одна для этого плана) центральная точка плана  и по две “звездные” точки для каждого фактора . –плечо “звездных” точек.При этом в каждой плоскости, содержащей ось Yи координатную осьi-того фактора (проходящей через центр плана), оказываются три значения факторахi  и три соответствующих значенияY.Общее количество точек в плане ОЦКП составляет  ,где для ОЦКП n0=1. При n> 2 в ОЦКП оказывается меньшее количество точек, чем в плане ПФЭ 3n. Число точек в плане
Графическое представление ОЦКП для n=3 приведено на рис. 13.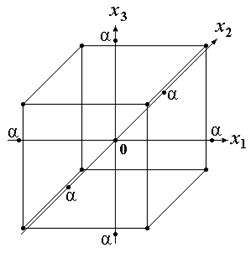 Рис. 13. ОЦКП при n=3 Для ортогонального плана необходимо, чтобы выполнялось соотношение  .Так как  , то для столбцовj=1, 2,….,m+1 должно выполняться условие .Это означает необходимость выполнения требования, чтобы сумма элементов любого столбца (кроме j=0), включая столбцы, соответствующие квадратам фактора, должна быть равна нулю. Это возможно, если члены столбцов, соответствующих квадратам факторов, преобразованы, иначе сумма квадратов факторов не может быть равна нулю. Преобразование элементов этих столбцов осуществляется в виде ,где а – величина, зависящая от числа факторов. Сумма элементов столбца, соответствующего квадратам факторов  .Откуда 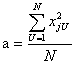 .В общем случае ортогональный центрально-композиционный план при трех (n) факторов имеет следующий вид  В ОЦКП каждый фактор фиксируется, в общем случае, на пяти уровнях (- , -1, 0, 1, + ).Для определения неизвестных “а” и “ ” нужно сформировать и решить систему из двух уравнений. Одно из них для “а” мы записали раннее. Другое уравнение получим из условия ортогональности для столбцов и  .После простейших преобразований с учетом того, что  – общее число опытов в плане, получаем соотношение .Соотношение для а при j=1, 2 или 3 может быть записано как (см. план) 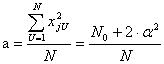 .Подставив его в последнее уравнение получаем  ,откуда константа преобразования а 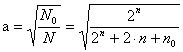 .Тогда  и плечо звездных точек .Например, для ОЦКП при числе факторов n=3 имеем следующие параметры плана  , , .Сам план принимает вид 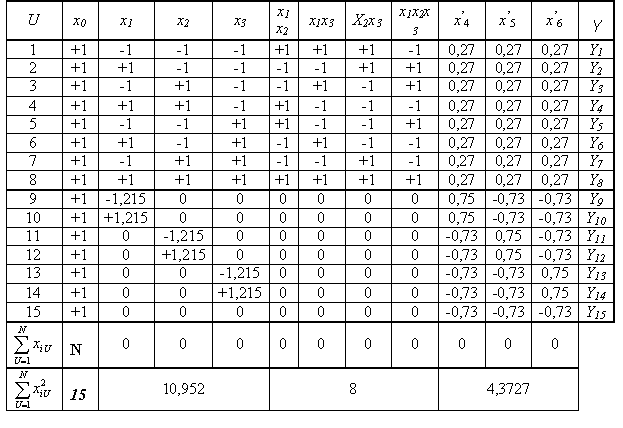 Очевидно, что план является ортогональным. В отличие от планов ПФЭ для ОЦКП сумма квадратов факторов разных столбцов не является одинаковой.По результатам опытов плана формируется полином 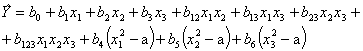 .Коэффициенты полинома 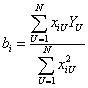 определяется как .Можно преобразовать полином к виду  ,где  Значения параметров ОЦКП при числе факторов n 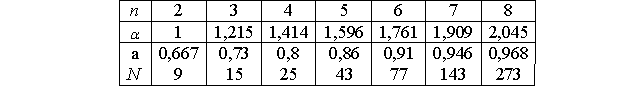 При n=2 ОЦКП совпадает с планом ПФЭ 23. Звездные точки ОЦКП в этом случае лежат на границах варьирования факторов. Если точки плана ПФЭ 2nвсегда лежат на окружности (поверхности шара, гипершара), то точки плана ОЦКП не лежат на какой-либо одной окружности (поверхности шара, гипершара). План ОЦКП не является насыщенным. Так, например, для n= 3 полином имеет одиннадцать членов со своими коэффициентами, но для их определения используются пятнадцать опытов. Список литературы1. Спирин Н.А., Лавров В.В. Методы планирования и обработки результатов инженерного эксперимента: конспект лекции Н.А. Спирина – Екатеринбург: ГОУ ВПО УГТУ – УПИ, 2004.- 257 с. 2. Налимов В.Н. Логические основания планирования эксперимента: учебник Е.А. Шалыгина -2-е изд. – М.: Колос, 2001. 3. Планирование эксперимента – studopedia.su |