Статистический пакет STATISTICA. Содержание Введение Теоретические сведения 1 Статистика. Виды статистического анализа 2 Статистический пакет statistica статистический анализ экономических данных в statistica 1 Практическое задание.
 Скачать 256.66 Kb.
|
2. Статистический анализ экономических данных в STATISTICA2.1 Практическое задание 1. Корреляционно-регрессионный анализ в STATISTICAПостановка задачи Руководство компании по результатам производственной деятельности 15 своих филиалов в различных городах России анализирует факторы, влияющие на производительность труда (y) и предполагает, что важнейшими из них являются следующие: x1 – среднегодовая стоимость основных фондов, тыс. руб. х2 – удельный вес рабочих высокой квалификации в общей численности рабочих, % х3– трудоемкость единицы продукции х4– среднегодовая численность рабочих x5– коэффициент сменности оборудования x6– удельный вес потерь от брака x7– среднегодовой фонд заработной платы, тыс. руб. Были собраны данные за последний год (см. таб. 3). Таблица 3 – Исходные данные
С использованием системы STATISTICA необходимо: 1) для y и переменных, соответствующих варианту (см. таб. 4), построить матрицу частных коэффициентов корреляции (корреляционную матрицу). Изобразить матрицу в графическом виде. Таблица 4 – Варианты заданий
2) построить линейное уравнение множественной регрессии, выбрав в качестве зависимой переменной – y, в качестве независимых – переменные хi, соответствующие варианту (см. таб. 4). 3) Определить коэффициент множественной корреляции и коэффициент детерминации R2полученной модели 4) Проверить значимость построенной модели (например, используя уровень значимости α=0,05). 5) Если модель значима дать оценку коэффициентов множественной регрессии на основе t-критерия, если tтабл(15-4-1)= tтабл(10)=2,2281 и уровня значимости α=0,05. 6) Пересчитать уравнение множественной регрессии используя только значимые факторы. 7) Проверить адекватность регрессионной модели (полученной на предыдущем этапе анализа). 8) Осуществить прогнозирование в соответствии с вариантом 9) Оформить отчет о проделанной работе используя распечатки отчета, полученного средствами пакета STATISTICA или в MS Word. Порядок выполнения задания В системе STATISTICA для построения корреляционной матрицы можно воспользоваться модулем Basic Statistics/Tables (Основные статистики и таблицы), выбрав процедуры   , используя в качестве переменных все исходные данные (Select all). И процедуру  для представления матрицы в графическом виде.По корреляционной матрице можно в первом приближении судить о тесноте связи факторных признаков х1, х2,…,xmмежду собой и с результативным признаком y, а также осуществлять предварительный отбор факторов для включения их в уравнение регрессии. При этом не следует включать в модель факторы, слабо коррелирующие с результативным признаком и тесно связанные между собой. Не допускается включать в модель функционально связанные между собой факторные признаки, так как это приводит к неопределенности решения. Выбор уравнения модели, в большинстве случаев, производятся среди функций перечисленных в таблице 3. В системе STATISTICA для построения линейного уравнения множественной регрессии можно воспользоваться модулем множественной регрессии 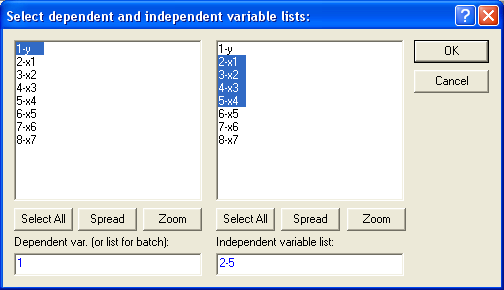 , определив зависимую (dependent) переменную y и независимые (independent) переменные х1, х2, x3, x4. Статистический вывод о пригодности (значимости) уравнения регрессии в системе Statistica обычно проверяется в следующей последовательности. Проводится общаяпроверка модели, целью которой является выяснение, объясняют ли х-переменные значимую долю изменения у. Определение значимости модели рекомендуется проводить по следующим методам (см. табл. 5). Таблица 5
Если регрессия неявляется значимой, то говорить больше не о чем. В при веденном примере модель значима, т.к. вычисленный уровень значимости модели р=0,000000<0,05.   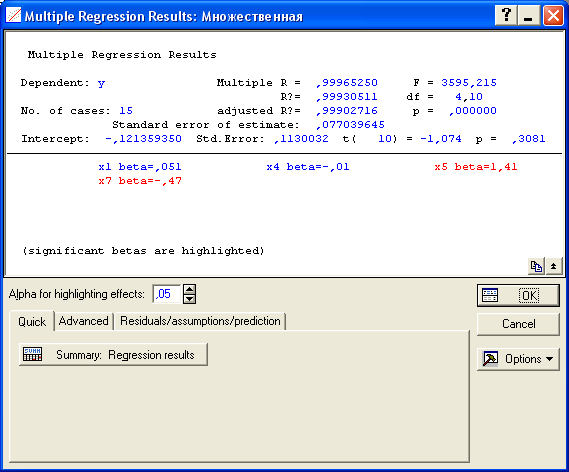 Осуществив переход к результатам регрессии (Summary: Regression results) получаем уравнение линейной множественной регрессии вида y(x1, x2, x3, x4)=6,9+0,07x1 –0,00035x2–2,08x3+0,00003x4:  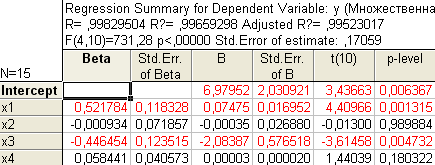 2. Если регрессия оказывается значимой, то существует взаимосвязь между параметром у и переменными х1, х2,…,xm. Однако остается неясно, каково влияние конкретных факторов х1, х2,…,xm на исследуемую функцию у. Можно продолжить анализ, используя t-тесты для отдельныхкоэффициентов регрессии а0, a1,a2,…,amс целью выяснить, насколько значимой является влияние той или иной переменной х на параметр у при условии, что все другие факторы хk остаются неизменными. Проверку на адекватность коэффициентов регрессии рекомендуется проводить по следующим эквивалентным методам (см. табл. 5). Таблица 5
Т.к. вычисленные уровни значимости p-level для коэффициентов, стоящих при x2 и x4 меньше 0,05, то они не значимы. К аналогичному выводу можно прийти, воспользовавшись t-критерием: t2(10)=-0,013<2,228 и t3(10)=1,44<2,228. С учетом этого факта, пересчитаем уравнение множественной регрессии, выбрав в качестве зависимой (dependent) переменную y и независимые (independent) переменные х1 и x3, коэффициенты при которых значимы: 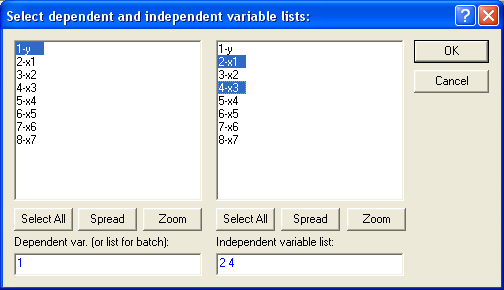 Получаем: 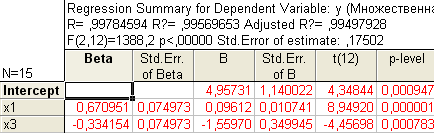 Т.о., уравнение регрессии имеет вид y(x1, x3)=4,957+0,096x1–1,559x3 Для выполнения прогнозов по полученному уравнению необходимо показать, что регрессионная модель адекватна результатам наблюдений. С этой целью можно воспользоваться критерием Дарбина-Уотсона, согласно которого, рассчитанный системой Statistica коэффициент dрасч необходимо сравнить с табличным значением dтабл(для совокупности объемом n=15, уровня значимости =0,05 и трех оцениваемых параметров регрессии, значение dтабл=1,75). Если dрасч>dтабл, то полученная модель адекватна и пригодна для прогнозирования. Для определения dрасч в Statistica в окне Residual Analysis на вкладке Advanced необходимо выбрать опцию Durbin-Watson statistic:  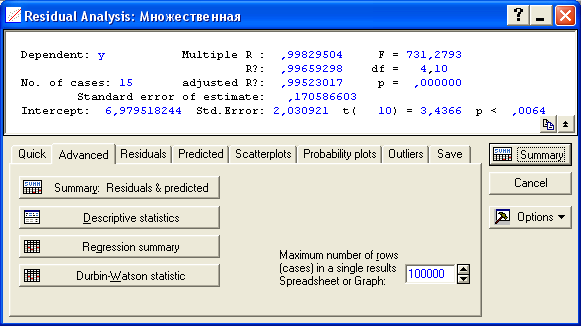 В рассматриваемом примере dрасч=1,2<1,75, следовательно, модель не желательно использовать для прогнозирования. 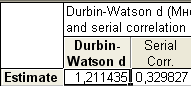 В случае, когда модель адекватна результатам наблюдения для выполнения прогноза в окне Multyple Regression Results вкладки Residuals/assumptions/prediction (Остатки/Предположения/Прогнозирование) выбрать опцию 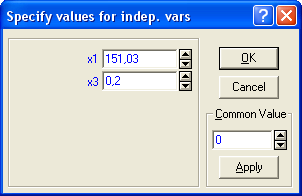 (прогнозирование зависимой переменной). Например, если в Москве среднегодовую стоимость основных фондов(переменная x1) повысить на 50 тыс. руб., а трудоемкость единицы продукции (переменная х3) уменьшить в два раза, то следует ожидать производительности труда равной 19,16 (увеличится на 19,16-14=5,16):  Прогнозируемое значение y  |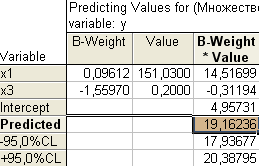
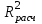сравнивается с табличными (критическими) значениями 
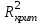, определяемым с использованием специальных таблиц по заданному уровню значимости (например, α =0,05). Если окажется, что