12 эконометрика (вариант 8). Содержание Задание 1 Сравнительный анализ метода наименьших квадратов и метода макмального правдоподобия при определении параметров эконометрических моделей. Ответ
 Скачать 168.04 Kb. Скачать 168.04 Kb.
|
|
Титульник Содержание Задание 1Сравнительный анализ метода наименьших квадратов и метода макϲᴎмального правдоподобия при определении параметров эконометрических моделей. Ответ Задание 2Данные каждого варианта определяется параметрами p1, p2. При выполнении контрольных заданий студент должен подставить там, где это необходимо, вместо буквенных параметров индивидуальные анкетные характеристики: p1 – число букв в полном имени студента (5 букв); p2– число букв в фамилии студента (9 букв). Исследуется зависимость производительности труда 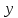 (т/ч) от уровня механизации работ (т/ч) от уровня механизации работ  (%), среднего возраста работников (%), среднего возраста работников 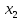 (лет) и энерговооруженности (лет) и энерговооруженности 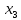 (кВт/100 работающих) по данным 14 промышленных предприятий. (кВт/100 работающих) по данным 14 промышленных предприятий.Таблица 1
В соответствии с вариантом задания, используя статистический материал, необходимо выполнить: 1. Выбор факторов для регрессионного анализа: 1) корреляционный анализ данных, включая проверку теста Фаррара –Глоубера на мультиколлинеарность факторов; 2) пошаговый отбор факторов методом исключения из модели статистически незначимых переменных; 3) проверка теста на «длинную» и «короткую» регрессии (при несоответствии результатов, полученных в пунктах 1 и 2). 2. Построение модели множественной регрессии с выбранными факторами, экономический анализ коэффициентов уравнения. 3. Оценку качества модели регрессии: 1) проверка статистической значимости уравнения с помощью F-критерия Фишера; 2) проверка предпосылки МНК о гомоскедастичности остатков; 3) оценка уровня точности модели. 4. Построение доверительных интервалов для результирующей переменной и определение компаний с заниженным и завышенным фактическим уровнем энерговооруженности (производительности «у»). Ранжирование компаний по степени их эффективности на основе результатов моделирования. 5. Оценку степени влияния факторов на результат с помощью коэффициентов эластичности, 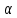 и и  коэффициентов. Выбор наиболее влияющего фактора. коэффициентов. Выбор наиболее влияющего фактора.6. Построение парной регрессии с наиболее влияющим фактором. Сравнение качества множественной и парной регрессий. 7. Прогнозирование энерговооруженности (производительности 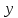 ) на основе модели парной регрессии с вероятностью 95% при условии, что прогнозное значение фактора увеличится на 10% относительно его среднего значения. ) на основе модели парной регрессии с вероятностью 95% при условии, что прогнозное значение фактора увеличится на 10% относительно его среднего значения.8. Графическое представление результатов моделирования. Решение В соответствии с исходными данными варианта составляем таблицу со значениями, которые необходимо обработать (таблица 2). Таблица 2 Исходные данные
1. Выбор факторов для регрессионного анализа: 1) Корреляционный анализ данных, включая проверку теста Фаррара –Глоубера на мультиколлинеарность факторов. На рис. 1 представлена матрица коэффициентов парной корреляции для всех переменных, участвующих в рассмотрении. Матрица получена с помощью инструмента Корреляция из пакета Анализ данных в MS Excel. Матрица коэффициентов парной корреляции 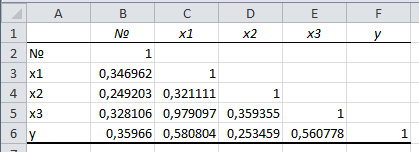 Рис. 1 – Матрица коэффициентов парной корреляции Визуальный анализ матрицы на рис. 1 позволяет установить: 1) переменная 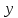 имеет довольно высокие парные корреляции с переменными имеет довольно высокие парные корреляции с переменными  и и 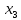 . Переменную . Переменную 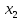 далее не будем рассматривать. далее не будем рассматривать.2) большинство переменных анализа демонстрируют довольно высокие парные корреляции, что обуславливает необходимость проверки факторов на наличие между ними мультиколлинеарности. Тем более, что одним из условий классической регрессионной модели является предположение о независимости объясняющих переменных. Для выявления мультиколлинеарности факторов выполним тест Фаррара-Глоубера по факторам  и и 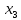 . .Проверка теста Фаррара-Глоубера на мультиколлинеарность факторов включает несколько этапов, реализация которых представлена ниже. Проверка наличия мультиколлинеарности всего массива переменных. Построим матрицу межфакторных корреляций  (рис. 2) и найдем её определитель (рис. 2) и найдем её определитель 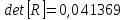 с помощью функции МОПРЕД(). с помощью функции МОПРЕД(). Рис. 2 – Матрица межфакторных корреляций R и значение определителя Определитель матрицы R стремится к нулю, что позволяет сделать предположение об общей мультиколлинеарности факторов. Подтвердим это предположение оценкой статистики Фаррара-Глоубера. Вычислим наблюдаемое значение статистики Фаррара – Глоубера по формуле: 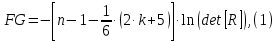 где  – количество наблюдений (заводов); – количество наблюдений (заводов);  – количество факторов (переменных анализа), подставляем значения в формулу (1): – количество факторов (переменных анализа), подставляем значения в формулу (1):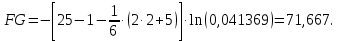 Фактическое значение этого критерия  сравниваем с табличным значением критерия сравниваем с табличным значением критерия  с с 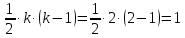 степенью свободы и уровне значимости степенью свободы и уровне значимости  . Табличное значение . Табличное значение  можно найти с помощью функции ХИ2.ОБР.ПХ(0,05; 1). можно найти с помощью функции ХИ2.ОБР.ПХ(0,05; 1).Так как 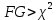 (71,667 > 3,841), то в массиве объясняющих переменных существует мультиколлинеарность. (71,667 > 3,841), то в массиве объясняющих переменных существует мультиколлинеарность.Проверка наличия мультиколлинеарности каждой переменной с другими переменными. Вычислим обратную матрицу  с помощью функции MS Excel МОБР (рис. 3). с помощью функции MS Excel МОБР (рис. 3).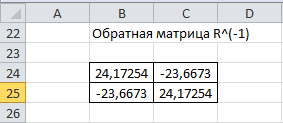 Рис. 3 – Обратная матрица  Вычисление F-критериев  где  – диагональные элементы матрицы – диагональные элементы матрицы  (рис. 4). (рис. 4). Рис. 4 – Значения F-критериев Фактические значения F-критериев сравниваются с табличным значением 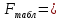 при при 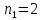 и и  степенях свободы и уровне значимости степенях свободы и уровне значимости  , где , где 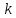 – количество факторов. – количество факторов.Так как все значения F-критериев больше табличного, то все исследуемые независимые переменные мультиколлинеарны с другими. Уточнение набора факторов, наиболее подходящих для регрессионного анализа, осуществим другими методами отбора. 2) Пошаговый отбор факторов методом исключения из модели статистически незначимых переменных В соответствии с общим подходом, пошаговый отбор следует начинать с включения в модель всех имеющихся факторов, то есть в нашем случае с трёхфакторной регрессии. Но мы не будем включать в модель факторы из заранее известных коллинеарных пар, а также фактор 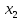 , имеющий слабую связь с , имеющий слабую связь с 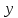 . Таким образом, пошаговый отбор факторов начнем с двухфакторного уравнения. Фрагмент двухфакторного регрессионного анализа представлен на рис. 5. . Таким образом, пошаговый отбор факторов начнем с двухфакторного уравнения. Фрагмент двухфакторного регрессионного анализа представлен на рис. 5.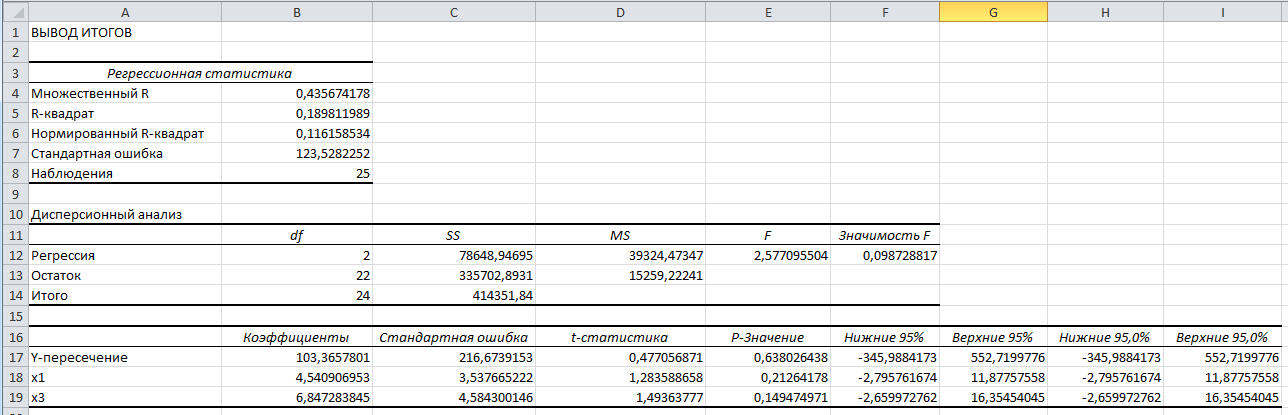 Рис. 5 – Фрагмент двухфакторного регрессионного анализа Статистически незначимыми  оказались три фактора (на рис. 1 они выделены жирным шрифтом). На следующем этапе пошагового отбора удаляем статистически незначимый фактор с наименьшим значением t-критерия, то есть фактор ОА (на рисунке 2 выделен цветом). оказались три фактора (на рис. 1 они выделены жирным шрифтом). На следующем этапе пошагового отбора удаляем статистически незначимый фактор с наименьшим значением t-критерия, то есть фактор ОА (на рисунке 2 выделен цветом).Аналогично поступаем до тех пор, пока не получим уравнение, в котором все факторы окажутся статистически значимыми. Этапы получения такого уравнения, то есть фрагменты соответствующих регрессионных анализов, представлены на рисунках 3, 4.
Рисунок 3. Фрагмент четырехфакторного регрессионного анализа
Рисунок 4. Фрагмент трехфакторного регрессионного анализа Из рисунка 3 видно, что уравнение с тремя факторами ОС, ПП и КО обладает статистически значимыми коэффициентами перед факторами (в нем незначим только свободный член), а, значит, и сами эти факторы статистически значимы. Таким образом, в результате пошагового отбора получено трехфакторное уравнение регрессии, все коэффициенты которого (кроме свободного члена) значимы при 5%-ном уровне значимости, вида где Y – ЧП, 3) Проверка теста на «длинную» и «короткую» регрессии По результатам пунктов 1) и 2) возникает необходимость выбора из двух регрессий: «длинной» – с тремя факторами (ОС, ПП и КО) и «короткой» – с одним фактором (ПП). Воспользуемся тестом на «длинную» и «короткую» регрессии. Этот тест используется для отбора наиболее существенных объясняющих переменных. Иногда переход от большего числа исходных показателей анализируемой системы к меньшему числу наиболее информативных факторов может быть объяснен дублированием информации, из-за сильно взаимосвязанных факторов. Стремление к построению более простой модели приводит к идее уменьшения размерности модели без потери её качества. Для этого используют тест проверки «длинной» и «короткой» регрессий. Рассмотрим две модели регрессии: yi= β0 + β1 xi1 +…+ βk xik+ε i (длинную) yi= β0 + β1 xi1 +…+ βk xik-q+εi (короткую) Предположим, что модель не зависит от последних q объясняющих переменных и их можно исключить из модели. Это соответствует гипотезе H0: βk-q+1 = βk-q+2…= βk =0, т.е. последние q коэффициентов Алгоритм проверки следующий: o Построить по МНК длинную регрессию по всем факторам o Построить по МНК короткую регрессию по первым o Вычислить F-статистику  o Если Fнабл>Fтабл (α, v1=q, v2=n-k-1), гипотеза отвергается (выбираем длинную регрессию), в противном случае – выбираем короткую регрессию. На основании данных нашего примера сравним две модели: «длинную» (с факторами 1) Построим длинную регрессию по трем факторам
Рисунок 5. Фрагмент регрессионного анализа для длинной (трехфакторной) регрессии 2) Построим короткую регрессию по одному фактору
Рисунок 6. Фрагмент регрессионного анализа для короткой (однофакторной) регрессии 3) Вычислим F-статистику 4) Так как 2) пошаговый отбор факторов методом исключения из модели статистически незначимых переменных; 3) проверка теста на «длинную» и «короткую» регрессии (при несоответствии результатов, полученных в пунктах 1 и 2). 2. Построение модели множественной регрессии с выбранными факторами, экономический анализ коэффициентов уравнения. 3. Оценку качества модели регрессии: 1) проверка статистической значимости уравнения с помощью F-критерия Фишера; 2) проверка предпосылки МНК о гомоскедастичности остатков; 3) оценка уровня точности модели. 1) Проверка статистической значимости уравнения с помощью F-критерия Фишера Расчетное значение F-критерия Фишера можно найти в регрессионном анализе (рисунок 7).
Рисунок 7. Фрагмент трехфакторного регрессионного анализа Так как 2) Проверка предпосылки МНК о гомоскедастичности остатков При проверке предпосылки МНК о гомоскедастичности остатков в модели множественной регрессии следует вначале определить, по отношению к какому из факторов дисперсия остатков более всего нарушена. Это можно сделать в результате визуального исследования графиков остатков, построенных по каждому из факторов, включенных в модель. Та из объясняющих переменных, от которой больше зависит дисперсия случайных возмущений, и будет упорядочена по возрастанию фактических значений при проверке теста Голдфельда-Квандта. Для трехфакторной модели нашего примера графики остатков относительно каждого из трех факторов имеют вид, представленный на рисунке (эти графики легко получить в отчете, который формируется в результате использования инструмента Регрессия в пакете Анализ данных).    Рисунок 8. Графики остатков по каждому из факторов трехфакторной модели На каждой из диаграмм ярко выражена направленность в распределении остатков, то есть непостоянство их дисперсии. В таком случае предпосылку о гомоскедастичности остатков следует проверять трижды, каждый раз упорядочивая значения переменных по возрастанию одного из факторов. Начнем с фактора, который имеет самое большое значение t-статистики, то есть с фактора ПП (t=10,282). Основные этапы теста Голдфельда-Квандта: 1. Упорядочим переменные Y – ЧП, 2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*109 3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 9). Для первой совокупности:
Для второй совокупности:
Рисунок 9. Фрагменты регрессионного анализа для первой и второй совокупностей соответственно 4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):
5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости Так как Аналогично обнаруживается наличие гетероскедастичности в остатках при упорядочении значений переменных по каждому из двух оставшихся факторов 4. Построение доверительных интервалов для результирующей переменной и определение компаний с заниженным и завышенным фактическим уровнем энерговооруженности (производительности «у»). Ранжирование компаний по степени их эффективности на основе результатов моделирования. 5. Оценку степени влияния факторов на результат с помощью коэффициентов эластичности, 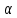 и и  коэффициентов. Выбор наиболее влияющего фактора. коэффициентов. Выбор наиболее влияющего фактора.6. Построение парной регрессии с наиболее влияющим фактором. Сравнение качества множественной и парной регрессий. 7. Прогнозирование энерговооруженности (производительности 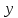 ) на основе модели парной регрессии с вероятностью 95% при условии, что прогнозное значение фактора увеличится на 10% относительно его среднего значения. ) на основе модели парной регрессии с вероятностью 95% при условии, что прогнозное значение фактора увеличится на 10% относительно его среднего значения.8. Графическое представление результатов моделирования. Список литературы |