Численные методы тест. Согласовано Утверждаю на заседании кафедры Зам директора по ур

• Название: Согласовано Утверждаю на заседании кафедры Зам директора по ур
• Дата: 07.11.2022
• Размер: 340.5 Kb.
• Имя файла: Численные методы тест.doc
• Тип: Документы; #774189

Согласовано: Утверждаю:

на заседании кафедры Зам. директора по УР

педагогики и __________Г. А. Словцова

информационных технологий «___»_____________2009г.

Зав. кафедрой ______ В.Н. Лёгкая

«___»___________2009г.

Численные методы

Тема 1. Приближенные числа и действия над ними.

Тема1. Приближенные числа и действия над ними.

1. 
   в
   
2. 
   г
   
3. 
   а
   
4. 
   б
   
5. 
   г
   
6. 
   а
   
7. 
   а
   
8. 
   б
   
9. 
   в
   
10. 
    б
    
11. 
    а
    
12. 
    б
    

1. Величина называется

а) погрешность метода;

б) погрешность округления;

в) абсолютная погрешность;

г) относительная погрешность.

2. Величина δ называется

а) погрешность метода;

б) погрешность округления;

в) абсолютная погрешность;

г) относительная погрешность.
3. Цифра числа называется верной (в широком смысле), если абсолютная погрешность этого числа не превосходит ____________ разряда, в котором стоит цифра

а) единицы;

б) десятка;

в) сотни;

г) тысячи.
4. a=2,91385, a=0,0097. В числе a верны в широком смысле цифры

а) 0,9,7;

б) 2,9,1;

в) 2,9,1,3;

г) 0,0,90,7.

5. ­­­____________ цифрами числа являются все цифры в его правильной записи, начиная с первой ненулевой слева

а) правильными;

б) верными;

в) сомнительными;

г) значащими.
6. Погрешность, обусловленная неточностью задания числовых данных, входящих в математическое описание задачи

а) неустранимая погрешность;

б) погрешность метода;

в) вычислительная погрешность;

г) результирующая погрешность.
7. Погрешность, являющаяся следствием несоответствия математического описания задачи реальной действительности

а) неустранимая погрешность;

б) погрешность метода;

в) вычислительная погрешность;

г) результирующая погрешность.
8. Погрешность, связанная со способом решения поставленной математической задачи

а) неустранимая погрешность;

б) погрешность метода;

в) вычислительная погрешность;

г) результирующая погрешность.
9. Погрешность обусловлена необходимостью выполнения арифметических операций над числами, усеченными до количества разрядов, зависящего от применяемой вычислительной техники.

а) неустранимая погрешность;

б) погрешность метода;

в) вычислительная погрешность;

г) результирующая погрешность.
10. Абсолютная погрешность округления с избытком числа 1,8 до целых равна

а) 0;

б) 0,2;

в) -0,2;

г) 0,1.
11. Известно, что π = 3,14… Точность приближенного равенства π ≈ 3,14 равна:

а) 3,14 ± 0,01;

б) 3,14;

в) 0,01;

г) 3,14 ± 0,1.

12. Известно, что 0,111 является приближенным значением для Относительная погрешность этого приближения равна:

а) ;
б) ;
в) ;
г) .
Тема 2. Приближенные решения алгебраических и трансцендентных уравнений.

Тема 2. Приближенные решения алгебраических и трансцендентных уравнений.

1. 
   б
   
2. 
   а
   
3. 
   б
   
4. 
   а
   
5. 
   в
   
6. 
   а
   
7. 
   в
   
8. 
   б
   

1. Отделить корень уравнения cosx = 2х.

а) [-1;1];

б) [0;1];

в) [1;2];

г) [2;3].
2. На рисунке изображен численный метод уравнений:
а) метод деления отрезка

б) метод хорд;

в) метод касательных;

г) метод интеграций.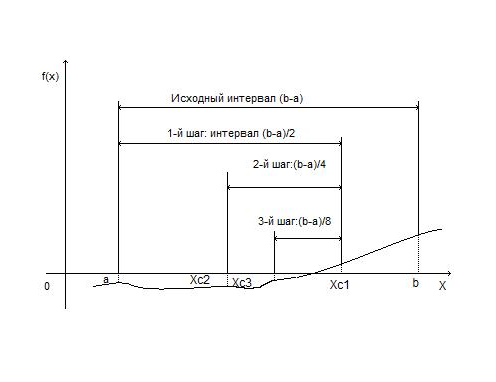
3. Метод, который приводит к решению алгебраических уравнений за конечное число арифметических операций, называется:

а) итерационный метод;

б) прямой метод;

в) метод хорд;

г) метод касательных.
4. Метод, в котором точное решение может быть получено лишь в результате бесконечного повторения единообразных действий, называется:

а) итерационный метод;

б) прямой метод;

в) метод хорд;

г) метод касательных.
5. В методе итераций процесс итераций продолжается до тех пор, пока для двух последовательных приближений и не будет обеспечено выполнение неравенства ( E – точность вычислений ):

а) | - | < E;

б) | - | ≥ E;

в) | - | ≤ E;

г) | - | > E.
6. На рисунки изображен метод:

1. 
   метод хорд;
   
2. 
   метод касательных;
   
3. 
   метод половинного деления;
   
4. 
   метод итераций.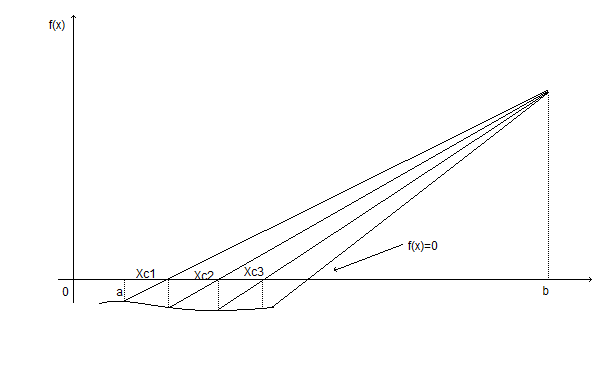
   

7. Методом Ньютона найти корень уравнения - 2х – 4=0 с точностью до 0,01:

1. 
   15,83;
   
2. 
   15,74;
   
3. 
   1,64;
   
4. 
   1,57.
   

8. Если функция f(x) представляет собой многочлен, то уравнение f(x) = 0 называется:

1. 
   трансцендентным;
   
2. 
   алгебраическим;
   
3. 
   линейным;
   
4. 
   комбинированным.
   

Тема 3. Решение систем линейных алгебраических уравнений.
Тема 3. Решение систем линейных алгебраических уравнений.

1. 
   г
   
2. 
   а
   
3. 
   а
   
4. 
   г
   
5. 
   б
   
6. 
   а
   
7. 
   б
   
8. 
   г
   
9. 
   в
   
10. 
    в
    

1. Даны матрацы , , det (AB) равен

а) -2;

б) 13;

в) -6,5;

г) -26.

2. Дана матрица А= 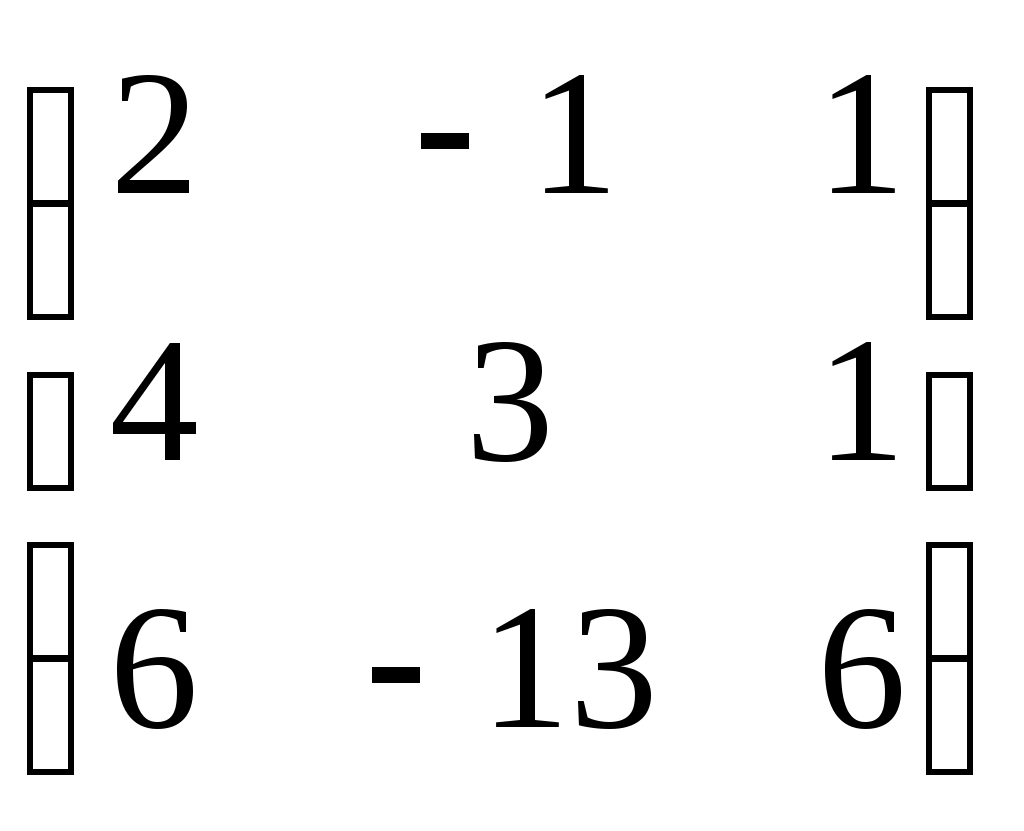. LU- разложение матрицы А:

1. 
   • ;
   
2. 
   • ;
   
3. 
   • ;
   
4. 
   •
   

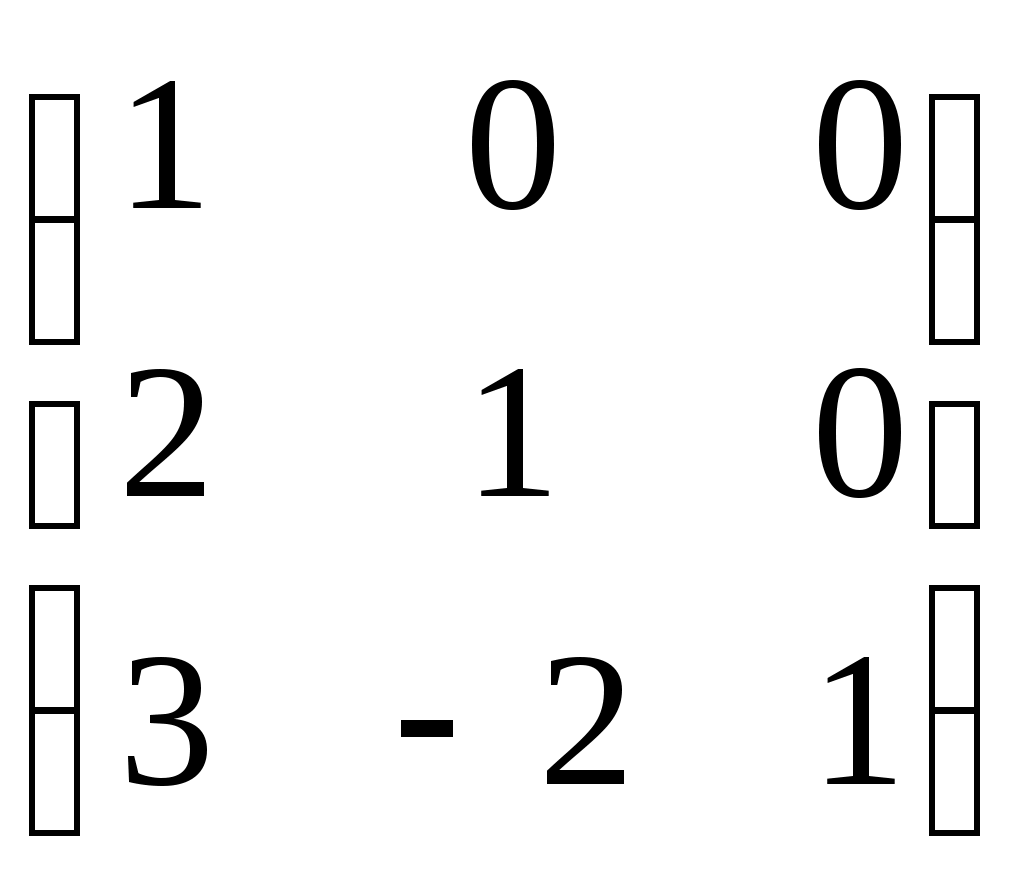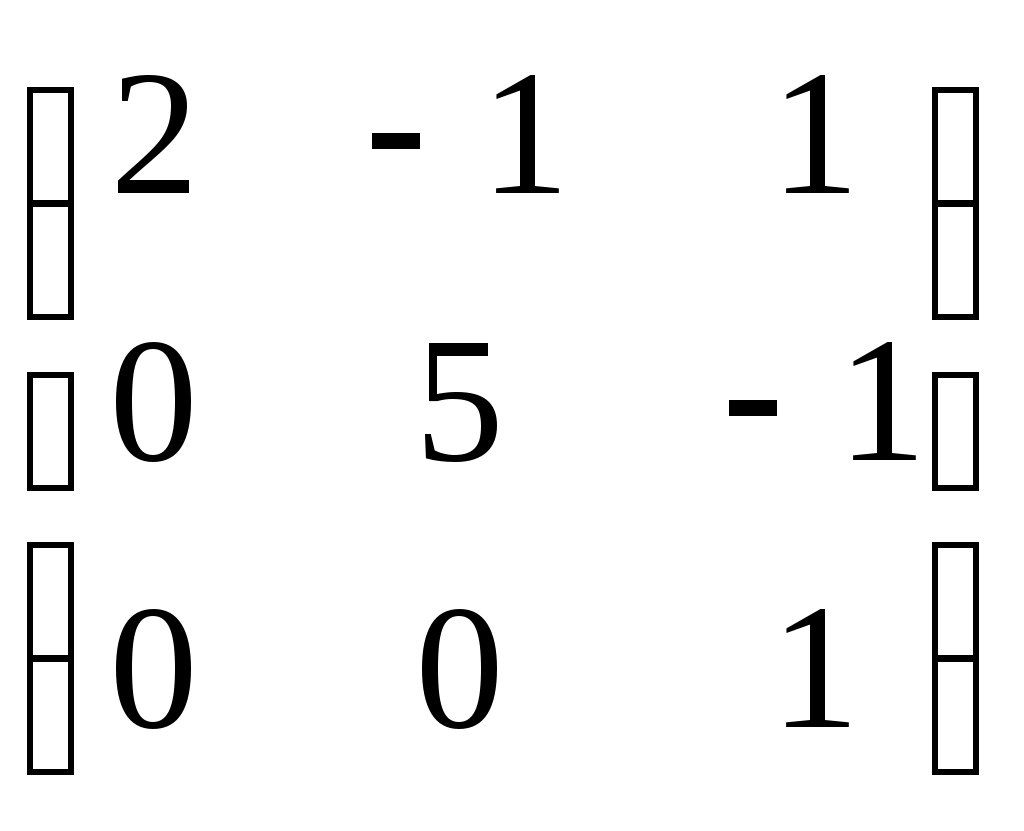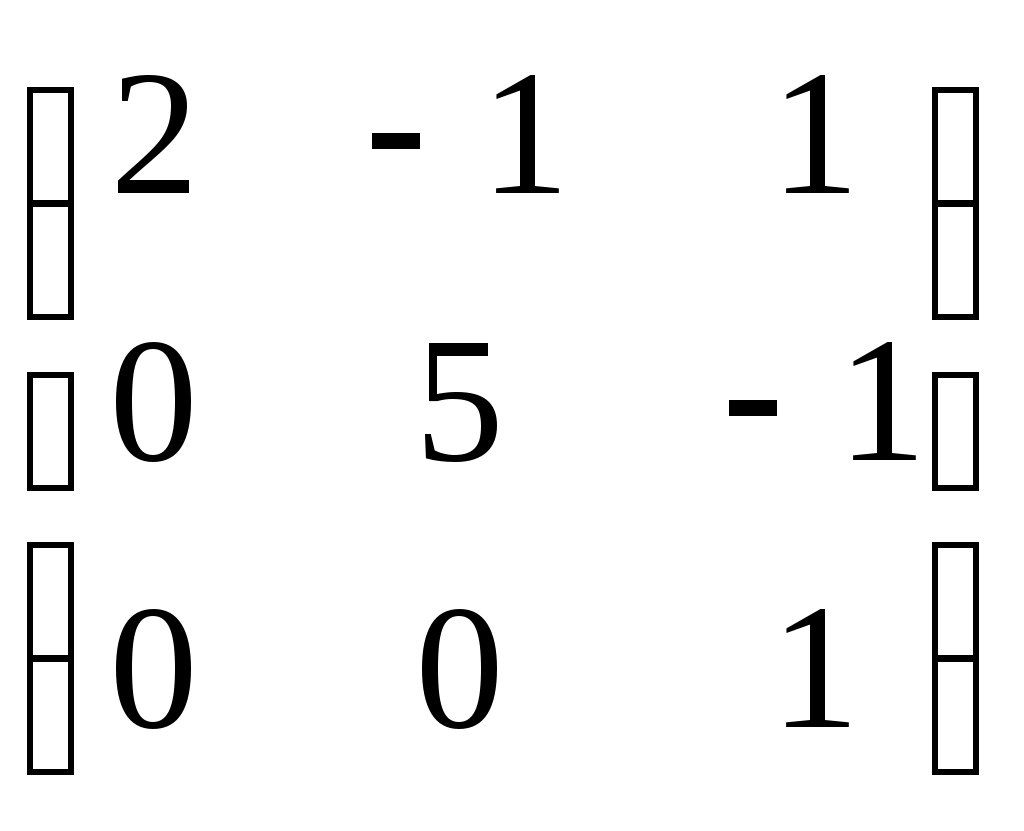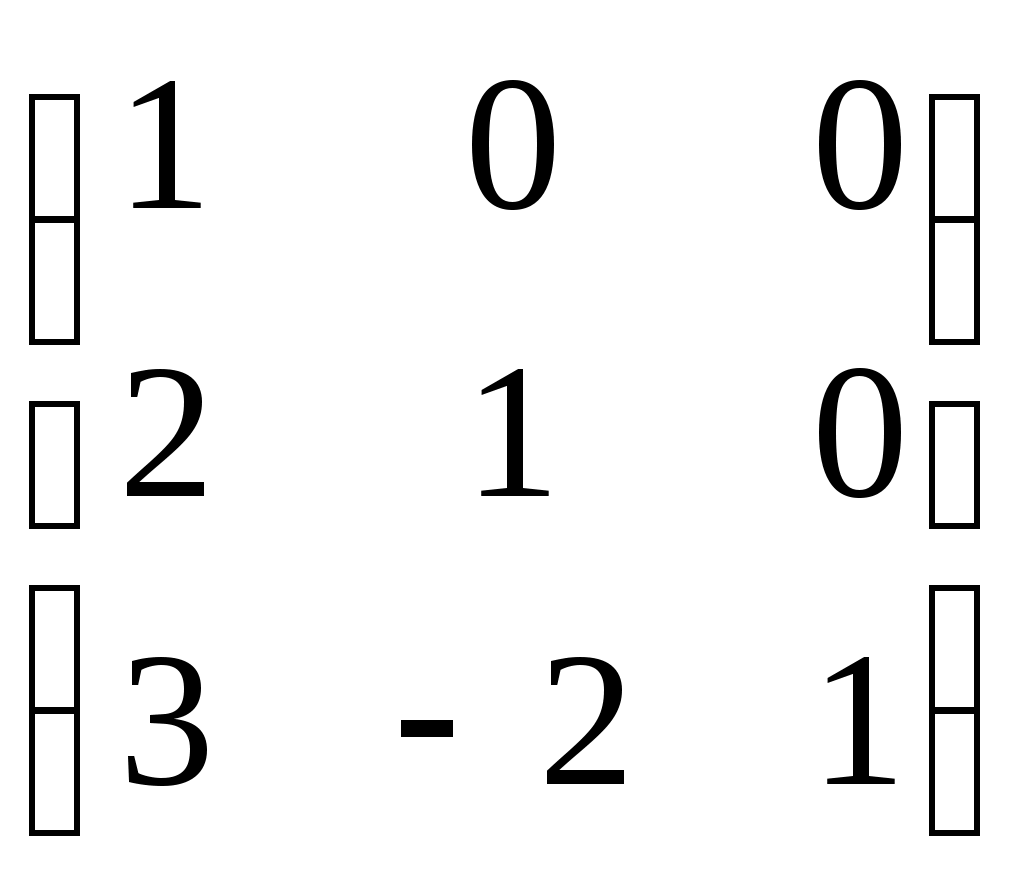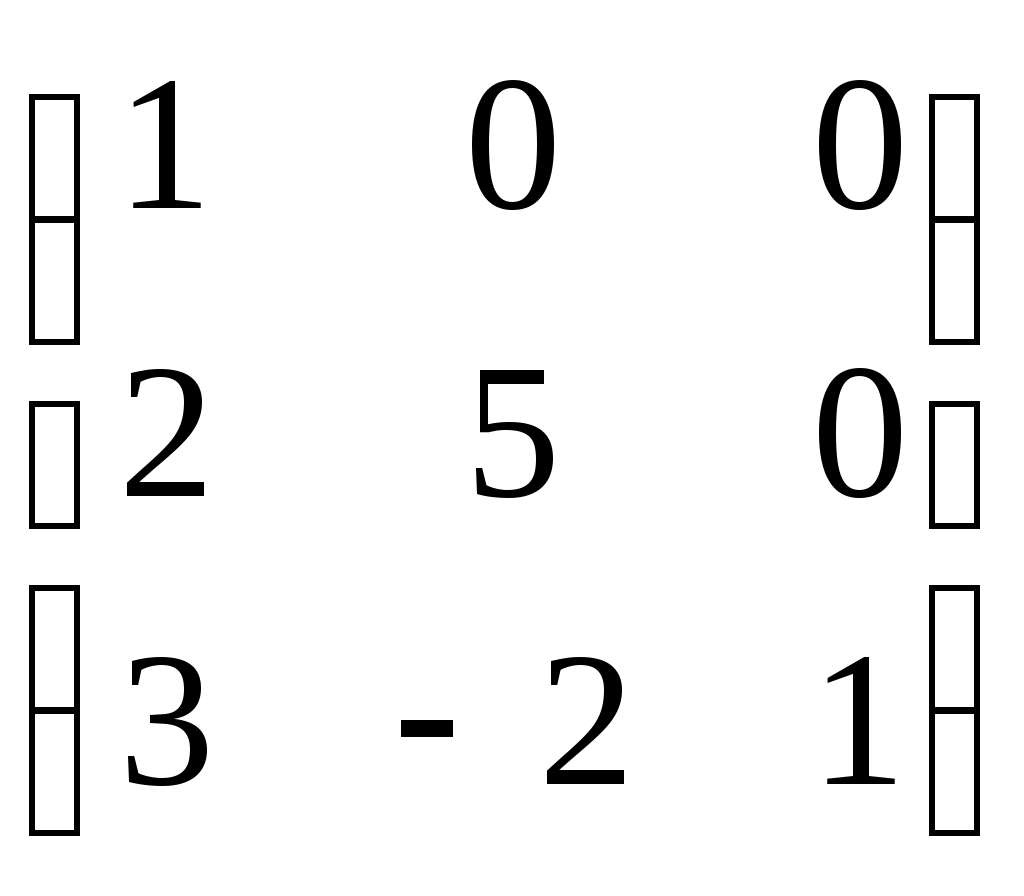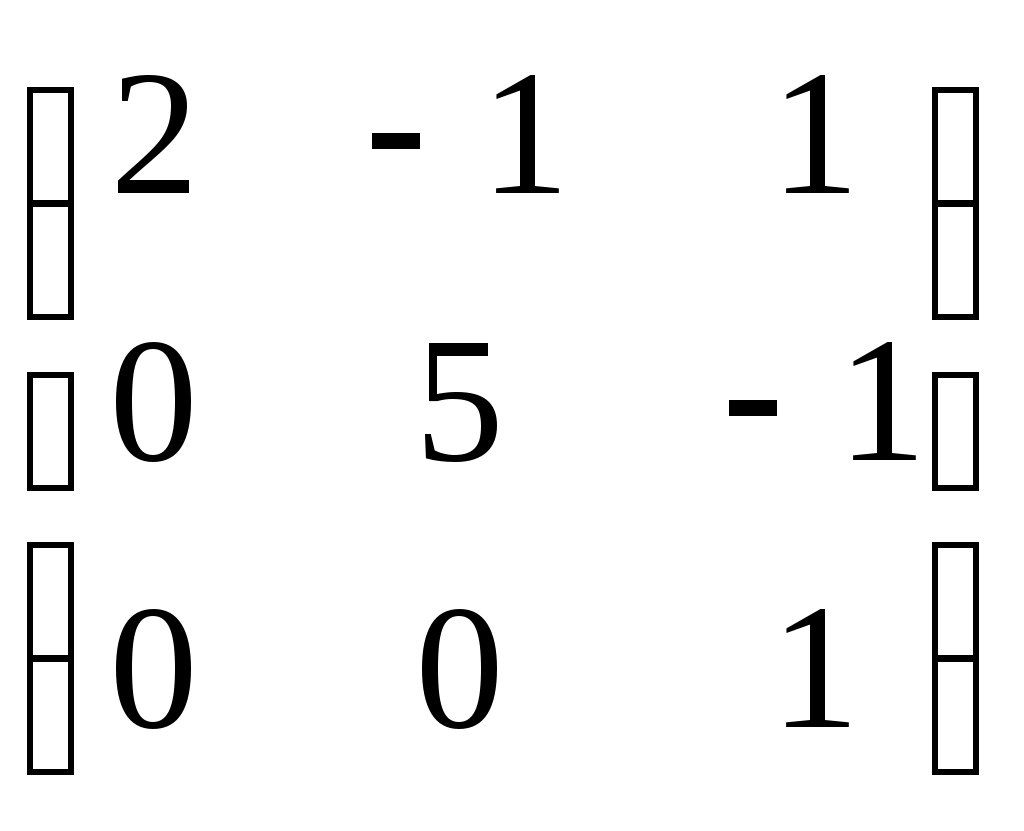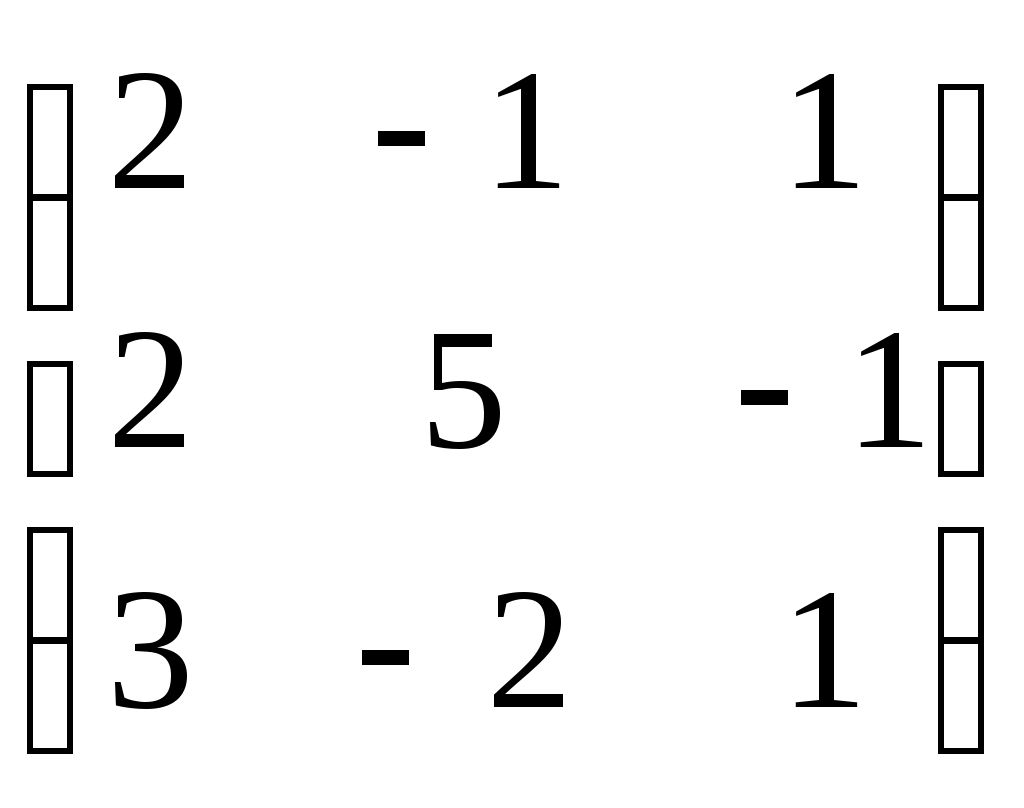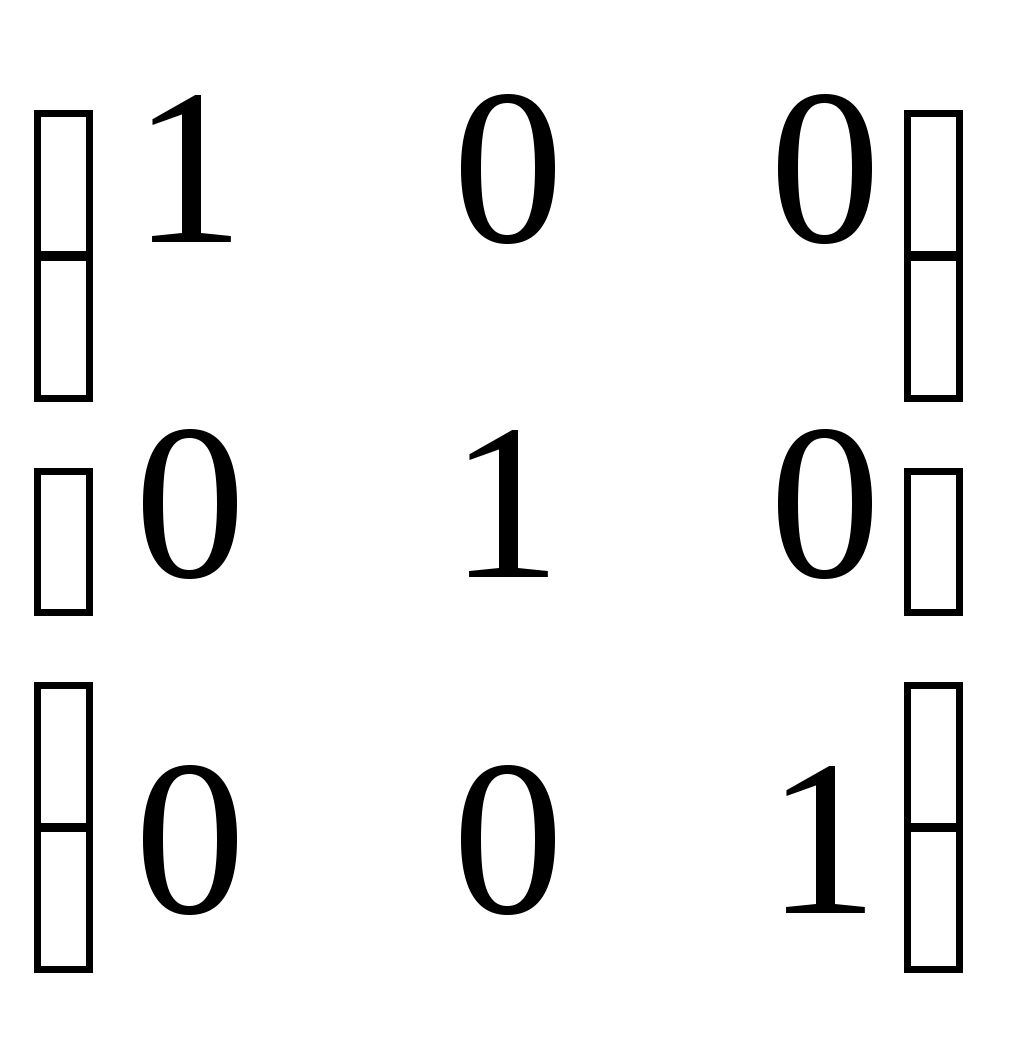3. Для того, что бы применить метод Зейделя к решению СЛАУ Ах=bс квадратной невырожденной матрицей А, необходимо предварительно преобразовать эту систему к виду:

1. 
   х=ВХ+с;
   
2. 
   х=АХ-b;
   
3. 
   х=АХ+с;
   
4. 
   х=ВХ+b.
   

4. Этот метод основан на предположении, что искомые неизвестные связаны рекуррентным соотношением = + :

1. 
   метод Зейделя;
   
2. 
   метод Гаусса;
   
3. 
   метод итераций;
   
4. 
   метод прогонки.
   

5. Метод последовательного исключения переменных:

1. 
   метод Зейделя;
   
2. 
   метод Гаусса;
   
3. 
   метод итераций;
   

г) метод прогонки.

6. Определитель матрицы равен произведению всех…….…….. при ее преобразовании методом Гаусса.

1. 
   ведущих элементов;
   
2. 
   элементов главной диагонали;
   
3. 
   ненулевых элементов;
   
4. 
   элементов, отличных от нуля.
   

7. Дана матрица А= 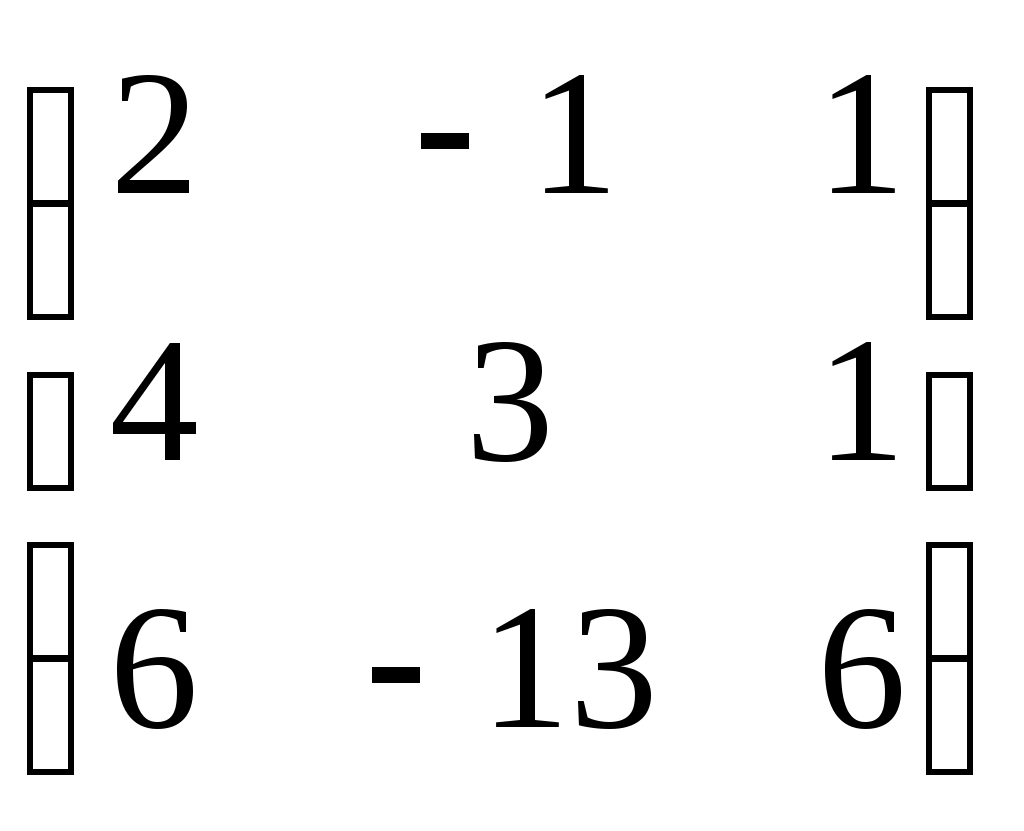. Методом Гаусса найдены элементы a и a , которые равны:

1. 
   2 и 1;
   
2. 
   5 и-1;
   
3. 
   4 и 2;
   
4. 
   -1 и 1;
   

8. Основная идея метода заключается в том, что при вычислении (k+1) -го приближения неизвестной учитываются уже вычисленные ране (k+1) – e приближения ( , , …, ).

1. 
   матричный метод;
   
2. 
   метод Крамера;
   
3. 
   метод Гаусса;
   
4. 
   метод Зейделя.
   

9. Метод используется для решения систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскание ранга матрицы.

1. 
   матричный метод;
   
2. 
   метод Крамера;
   
3. 
   метод Жордана-Гаусса;
   
4. 
   метод Зейделя.
   

10. К приближенным методам решения систем линейных уравнений относятся:

1. 
   метод Крамера;
   
2. 
   метод Гаусса;
   
3. 
   метод простой итерации;
   
4. 
   матричный метод.
   

Тема 4. Интерполирование и экстраполирование функций.

Тема 4. Интерполирование и экстраполирование функций.

1. 
   б
   
2. 
   а
   
3. 
   г
   
4. 
   в
   
5. 
   в
   
6. 
   а
   
7. 
   б
   
8. 
   в
   
9. 
   а
   
10. 
    в
    

1. Способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений:

1. 
   экстраполяция;
   
2. 
   интерполяция;
   
3. 
   метод прогонки;
   
4. 
   метод конечных элементов.
   

2. Интерполяционный многочлен Лагранжа для функций, заданной таблично

х	1	2	3	5
y	1	5	14	81

равен:

1. 
   (x) = x³-2x²+3x-1;
   
2. 
   (x) = -2x³+3x²+5x;
   
3. 
   (х) = x³+2x²+3x+5;
   
4. 
   (x)= 5 - 14x³+81x²+1.
   

3. Конечная разность первого порядка Δ функция y = х²+х+3 при начальном значении =0 и шаге h=1 равна:

1. 
   -2;
   
2. 
   3;
   
3. 
   1;
   
4. 
   2.
   

4. По таблице значений функции

х	0	1	2
y	3	5	8

составлена таблица конечных разностей:

х	y	Δy	Δ²y
0	3
		2
1	5		1
		3
2	8

Тогда приближенное значение производной функции f ´(x) = , где , в точке х=0,5 , равно

1. 
   2;
   
2. 
   3;
   
3. 
   1;
   
4. 
   4.
   

5. Интерполяционный многочлен Лагранжа для функции, заданной таблицей значений

х	1	3	4
f(x)	12	4	6

имеет вид:

1. 
   (х) = х³+3х²+4;
   
2. 
   (x) = 12x³+4x²+6x;
   
3. 
   (x) = 2x²-12x+22;
   
4. 
   (x) = x²-4x+10.
   

6. Вычисление значений таблично заданной функции за пределами диапазона значений аргумента, отраженного в таблице называется:

1. 
   экстраполяция;
   
2. 
   интерполяция;
   
3. 
   метод прогонки;
   

г) метод конечных элементов.
7. Интерполяция стандартно производятся многочленами, степень которых на ……… меньше числа узлов:

1. 
   порядок n-1;
   
2. 
   единицу;
   
3. 
   порядок n;
   
4. 
   половину.
   

8. Конечная разность вперед порядка k ≥ 1 определяется следующим образом:

1. 
   ;
   
2. 
   ;
   
3. 
   ;
   
4. 
   .
   

9.Функция y=f(x) приближается интерполяционным многочленом Ньютона 1-ой степени по узлам каков коэффициент при старшей степени Х

1. 
   
   

2. 
   
   

3. 
   
   

4. 
   
   

10. Является ли интерполяционным сплайном многочлен N, построенной по заданным значениям функций в узлах

1. 
   нет, т.к. на разных элементарных отрезках получается один и тот же многочлен;
   
2. 
   нет, т.к. сплайн не может быть многочленом высокой степени;
   
3. 
   да, это сплайн степени n дефекта 0;
   
4. 
   да, сплайн степени n дефекта N.
   

Тема 5. Численное интегрирование.

Тема 5. Численное интегрирование.

1. 
   г
   
2. 
   а
   
3. 
   а
   
4. 
   б
   
5. 
   а
   
6. 
   а
   
7. 
   б
   
8. 
   б
   
9. 
   а
   
10. 
    г
    

1. Приближенное значение интеграла (полагая n=5), вычисленное по формуле левых прямоугольников, равно:

1. 
   15;
   
2. 
   5;
   
3. 
   12,5;
   
4. 
   10.
   

2. Используя метод левых прямоугольников вычислен определенный интеграл (полагая n=4), который приблизительно равен:

1. 
   1,5744;
   
2. 
   1,6024;
   
3. 
   1,1053;
   
4. 
   1,7845.
   

3. S =

1. 
   метод Симпсона;
   
2. 
   метод трапеций;
   
3. 
   формула левых прямоугольников;
   
4. 
   формула правых прямоугольников.
   

4. S ≈

1. 
   метод прямоугольников;
   
2. 
   метод трапеции;
   
3. 
   метод парабол;
   
4. 
   метод Симпсона.
   

5. Приближенное значение интеграла при n=4, вычисленное по формуле трапеции, равно:

1. 
   0,783;
   
2. 
   0,5;
   
3. 
   0,645;
   
4. 
   0,812.
   

6. Приближенное значение интеграла при h=0,25 , вычисленное по формуле Симпсона, равно:

1. 
   0,782:
   
2. 
   0,702;
   
3. 
   0,5;
   
4. 
   0,645.
   

7.

1. 
   формула Гаусса;
   
2. 
   формула Ньютона─Котеса;
   
3. 
   формула Симпсона;
   
4. 
   формула Лагранжа.
   

8. Традиционно при получении квадратных формул Гаусса в исходном интеграле выполняется замена переменной, переводящая интеграл по отрезку [a;b] в интеграл по отрезку:

1. 
   [b;a];
   
2. 
   [-1;1];
   
3. 
   [0;1];
   
4. 
   [1;2].
   

9. Система позволяет благодаря графическим возможностям проиллюстрировать геометрический смысл интеграла

1. 
   Match Cad;
   
2. 
   Derive;
   
3. 
   Mathematica;
   
4. 
   Maple.
   

10. S ≈

1. 
   метод трапеции;
   
2. 
   метод левых прямоугольников;
   
3. 
   метод правых прямоугольников;
   
4. 
   метод средних прямоугольников.
   

Тема 6. Численное решение обыкновенных дифференциальных уравнений.
Тема 6. Численное решение обыкновенных дифференциальных уравнений.

1. 
   а
   
2. 
   б
   
3. 
   а
   
4. 
   в
   
5. 
   в
   
6. 
   г
   
7. 
   б
   
8. 
   а
   
9. 
   а
   
10. 
    г
    

1. Если последовательные значения функции, являющейся решением задачи Коши для дифференциального уравнения y´=f(x,y) с начальными условиями y ( ) = , x= , находятся по методу Эйлера , то , определяемая уравнением y´= х + y, при и шаге h=0,1 равно:

1. 
   1,1;
   
2. 
   2;
   
3. 
   1,2;
   
4. 
   1,3.
   

2. Методом Эйлера для дифференциального уравнения y´=y-x с начальным условием на отрезке [0;1,5] при h=0,25 равно:

1. 
   2;
   
2. 
   2,28125;
   
3. 
   1,45;
   
4. 
   4,75275.
   

3. При интегрировании методом Эйлера дифференциального уравнения y´=y-x с начальным условием на отрезке [0;1,5] при h=0,25 Δ равно:

1. 
   0,406;
   
2. 
   0,25;
   
3. 
   0,375;
   
4. 
   0,445.
   

4. Локальная оценка метода Рунге-Кутты 4го порядка точности имеет вид:

1. 
   | r | ≤ Ch³ ;
   
2. 
   | r | ≤ Ch²;
   
3. 
   | r | < C ;
   
4. 
   | r | ≤ C .
   

5.

1. 
   метод Зейделя;
   
2. 
   метод Эйлера;
   
3. 
   метод Рунге-Кутта второго порядка;
   
4. 
   метод Рунге-Кутта 4го порядка.
   

6. , где i=0,1;…,

1. 
   метод Зейделя;
   
2. 
   метод Эйлера;
   
3. 
   метод Рунге-Кутта второго порядка;
   
4. 
   метод Рунге-Кутта 4го порядка.
   

7. Δ

1. 
   метод Зейделя;
   
2. 
   метод Эйлера;
   
3. 
   метод Рунге-Кутта второго порядка;
   
4. 
   метод Рунге-Кутта 4го порядка.
   

8. Метод Эйлера

1. 
   одношаговый метод;
   
2. 
   n-шаговый метод;
   
3. 
   i-шаговый метод;
   
4. 
   многошаговый метод.
   

9. Метод Рунге-Кутта

1. 
   одношаговый метод;
   
2. 
   n-шаговый метод;
   
3. 
   i-шаговый метод;
   
4. 
   многошаговый метод.
   

10. Метод Адамса

1. 
   одношаговый метод;
   
2. 
   n-шаговый метод;
   
3. 
   i-шаговый метод;
   
4. 
   многошаговый метод.
   

Тема 7. Численное решение задач оптимизации.
Тема 7. Численное решение задач оптимизации.

1. 
   а
   
2. 
   б
   
3. 
   а
   
4. 
   б
   
5. 
   в
   
6. 
   г
   
7. 
   а
   
8. 
   а
   
9. 
   а
   
10. 
    а.
    

1. Воспроизводят геометрические и физические свойства оригинала и всегда имеют реальное воплощение

а) материальные модели;

б) информационные модели;

в) вербальные модели;

г) знаковые модели.
2. Совокупность информации, характеризующая свойства и состояние объекта, процесса, явления, а также взаимосвязь с внешним миром

а) материальные модели;

б) информационные модели;

в) вербальные модели;

г) знаковые модели.
3. Описание задачи, определение цели моделирования это:

а) постановка задачи;

б) разработка модели;

в) компьютерный эксперимент;

г) анализ результатов моделирования.
4. Выяснение свойств, состояний, действия и других характеристик элементарных объектов. Формирование представления об элементарных объектах

а) постановка задачи;

б) разработка модели;

в) компьютерный эксперимент;

г) анализ результатов моделирования.
5. Процесс проверки правильности модели

а) постановка задачи;

б) разработка модели;

в) компьютерный эксперимент;

г) анализ результатов моделирования.
6. Принятие решения, которое должно быть выработано на основе всестороннего анализа

полученных результатов

а) постановка задачи;

б) разработка модели;

в) компьютерный эксперимент;

г) анализ результатов моделирования.

7. Даны матрицы A=(9 6 3 1), B=(-2 3 -5 7). Произведение AB^Т равно

а) -8;

б) ;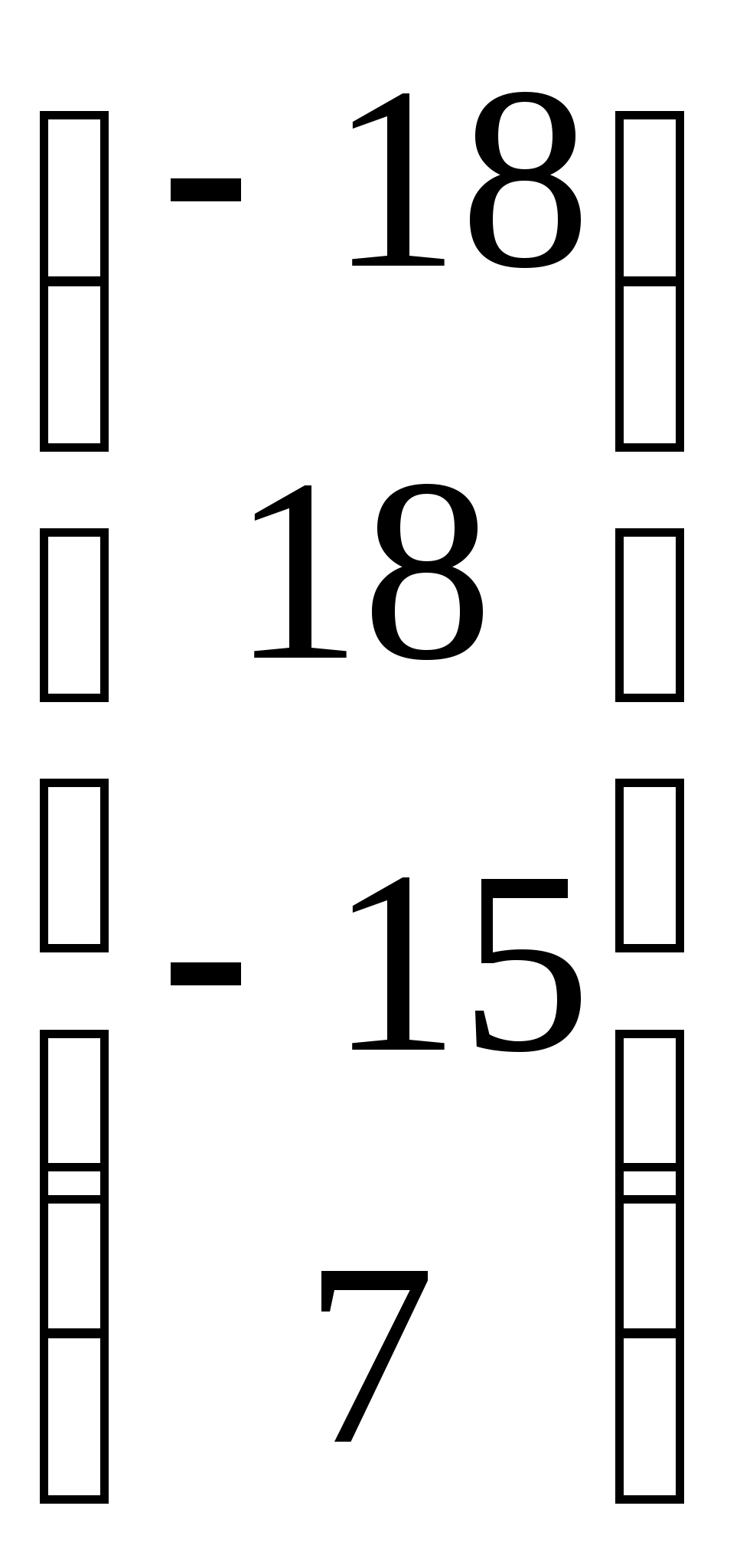

в) (-18 18 -15 7);

г) 6.
8. Исходное опорное решение системы ограничений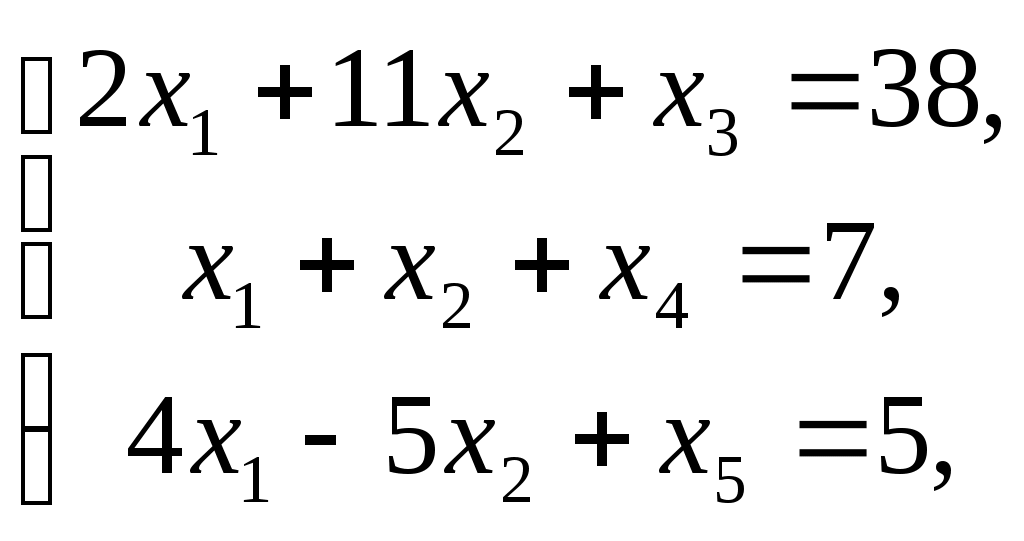

1. 
   (0,0,38,7,5);
   
2. 
   (38,7,5,0,0) ;
   
3. 
   (0,38,7,5,0) ;
   
4. 
   (38,0,7,5,0).
   

9. Оптимальное решение задачи f=2 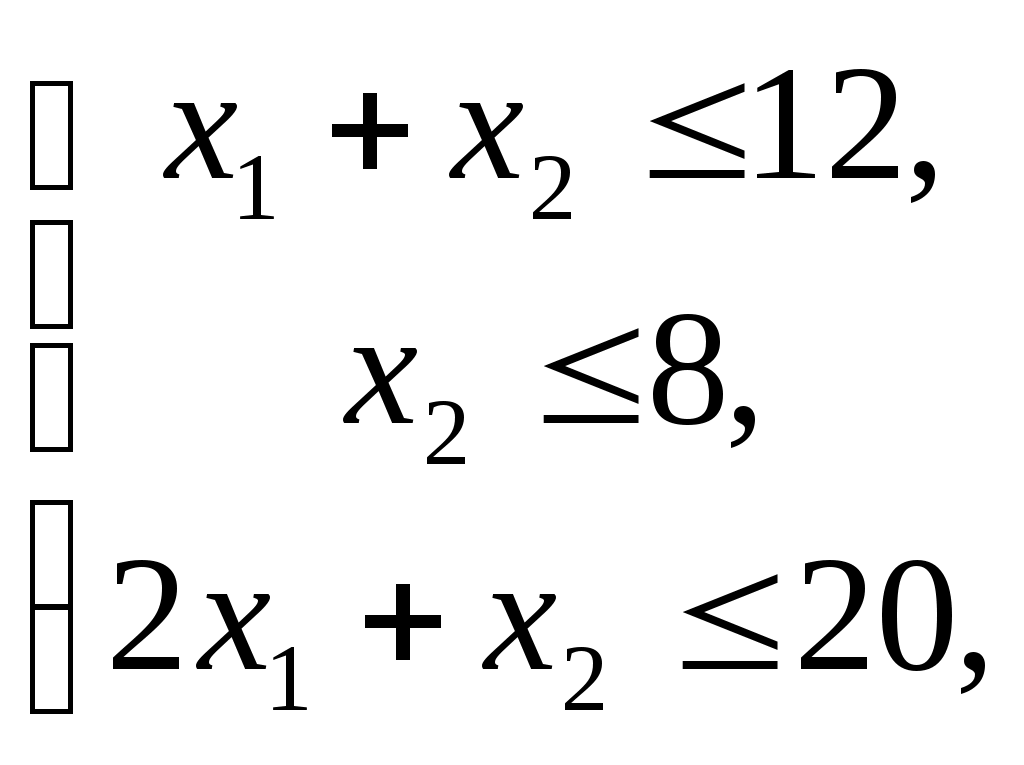так,



равно

1. 
   40;
   
2. 
   60;
   
3. 
   80;
   
4. 
   100.
   

10. Перемещение по ребрам многоугольникам допустимых решений от одной вершины к другой. Геометрическая интерпретации

1. 
   симплексного метода;
   
2. 
   метода Симпсона;
   
3. 
   метода Гаусса;
   
4. 
   метод Зейделя.
   

Эталоны ответов.

Тема1. Приближенные числа и действия над ними.

11. 
    в
    
12. 
    г
    
13. 
    а
    
14. 
    б
    
15. 
    г
    
16. 
    а
    
17. 
    а
    
18. 
    б
    
19. 
    в
    
20. 
    б
    
21. 
    а
    
22. 
    б
    

Тема 2. Приближенные решения алгебраических и трансцендентных уравнений.

23. 
    б
    
24. 
    а
    
25. 
    б
    
26. 
    а
    
27. 
    в
    
28. 
    а
    
29. 
    в
    
30. 
    б
    

Тема 3. Решение систем линейных алгебраических уравнений.

31. 
    г
    
32. 
    а
    
33. 
    а
    
34. 
    г
    
35. 
    б
    
36. 
    а
    
37. 
    б
    
38. 
    г
    
39. 
    в
    
40. 
    в
    

Тема 4. Интерполирование и экстраполирование функций.

41. 
    б
    
42. 
    а
    
43. 
    г
    
44. 
    в
    
45. 
    в
    
46. 
    а
    
47. 
    б
    
48. 
    в
    
49. 
    а
    
50. 
    в
    

Тема 5. Численное интегрирование.

51. 
    г
    
52. 
    а
    
53. 
    а
    
54. 
    б
    
55. 
    а
    
56. 
    а
    
57. 
    б
    
58. 
    б
    
59. 
    а
    
60. 
    г
    

Тема 6. Численное решение обыкновенных дифференциальных уравнений.

61. 
    а
    
62. 
    б
    
63. 
    а
    
64. 
    в
    
65. 
    в
    
66. 
    г
    
67. 
    б
    
68. 
    а
    
69. 
    а
    
70. 
    г
    

Тема 7. Численное решение задач оптимизации.

71. 
    а
    
72. 
    б
    
73. 
    а
    
74. 
    б
    
75. 
    в
    
76. 
    г
    
77. 
    а
    
78. 
    а
    
79. 
    а
    
80. 
    а.