Функции. Функции обучения математике. Современное школьное
 Скачать 73.5 Kb. Скачать 73.5 Kb.
|
|
Функции обучения математике. Гуманизация и гуманитаризация математического образования. Содержание математического образования. Основные содержательно-методические линии школьного курса математики. СОВРЕМЕННОЕ ШКОЛЬНОЕ МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ Образование это организованный процесс постоянной передачи предшествующими поколениями последующим социально значимого опыта. Это понятие используется в философии, психологии, педагогической науке и в практике школьного обучения. Современное образование характеризуется усилением внимания к ученику, к его саморазвитию и самопознанию, общечеловеческим знаниям, обращенностью ученика к окружающему миру и себе, к воспитанию умения искать и находить свое место в жизни. Образование представляет собой процесс и результат овладения учащимися системой знаний (математических), познавательных умений и навыков, формирования на этой основе мировоззрения, нравственных и других качеств личности, развития ее творческих сил и способностей. Образование рассматривается в двух аспектах: социальном,отражающем требования общества к образованию; личностном, определяющем цели образования для каждой личности индивидуально). Образованную личность характеризуют: определенность и конкретность мышления; широта и гибкость мышления; умение ориентироваться в широком круге проблем и желание решать их; разнообразие потребностей; способность прогнозировать развитие событий и моделировать свою деятельность; высокая работоспособность и т.д. Основной целью математического образования является воспитание у школьников умения рассматривать явления реального мира с математической точки зрения, видеть практическую направленность математики и её приложений. Математическое образование как феномен общечеловеческой культуры является отражением истории развития человеческой мысли. Вся современная наука (физика и химия, биология и экономика, лингвистика и социология) не только использует математические методы в своем развитии, но и строится по математическим законам. Значение математического образования для формирования духовной сферы человека, его интеллектуальных и нравственных ценностей велико. В процессе обучения математике воспитывается настойчивость, целеустремленность, дисциплина, критичность мышления, развиваются математические способности, формируется понимание красоты математических утверждений, развивается пространственное воображение и др. Современная перестройка системы математического образования осуществляется на основе: демократизации (обеспечение права каждому ученику на получение полноценного математического образования); гласности (наличие открытой и полной информации о состоянии преподавания и результативности обучения математике); децентрализации (право регионов и школ на выбор программ, учебных пособий, на самостоятельное решение проблем математического образования); реализма (реальная политика в области математического образования). ВЕДУЩИЕ ЦЕЛИ ОБУЧЕНИЯ МАТЕМАТИКЕ В ШКОЛЕ Цели образования один из определяющих компонентов педагогической системы. Они зависят от современных условий, социального заказа общества к образованию граждан. Основныецели обучения математике (в широком смысле): Овладение всеми учащимися элементами мышления и деятельности, которые наиболее ярко проявляются в математической ветви человеческой культуры и которые необходимы каждому для полноценного развития в современном обществе. Создание условий для зарождения интереса к математике и развития математических способностей одаренных школьников. Соответственно целям обучения выделяются уровни обучения математике (рис. 2): Цели обучения математике отражают общедидактические цели и вместе с тем учитывают специфику данного учебного предмета математики. Разработка целей обучения является довольно непростым для учителя делом. Цели обучения математике (в узком смысле) подразделяются на несколько групп: образовательные, воспитательные и развивающие. 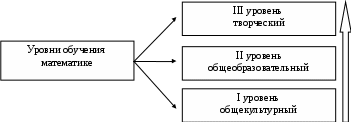 Рис. 2. Уровни обучения математике Образовательные (прогностические, обучающие) цели: овладение учащимися системой математических знаний, умений и навыков, дающей представление о предмете математики, о математических приемах и методах познания, применяемых в математике. Основным документом, в котором фиксируются цели обучения математике, является программа по математике. Общая характеристика целей обучения дается в объяснительной записке к программе по математике. Существуют различные способы конкретного представления целей обучения. Образовательные цели, например, формулируются в виде требований к уровню математической подготовки учащихся. В программе по математике для этого выделяется специальный раздел «Требования к математической подготовке учащихся». Другой раздел программы «Содержание обучения» представляет образовательные цели в еще более конкретной форме. Дальнейшей конкретизацией образовательных целей служит учебник или учебное пособие. Конкретный уровень представления образовательных целей имеет место в экзаменационных билетах для учащихся, контрольных работах. В методических пособиях часто формулируются цели обучения для отдельных тем, уроков. Образовательные цели призваны разграничить основной и второстепенный материал и помочь учителю рационально распределить учебное время. Воспитательные (личностно-ориентированные) цели: воспитание активности, самостоятельности, ответственности; воспитание нравственности, культуры общения; воспитание эстетической культуры, воспитание графической культуры школьников. Воспитательные цели должны быть тесно связаны с содержанием урока математики. Это могут быть цели: по формированию мировоззрения; сознательного отношения к учебе; развитию познавательной активности обучающихся, культуры учебного труда; воспитания сознательности в процессе обучения математике; расширения политехнического кругозора обучающихся; подготовки к сознательному выбору профессии и т.д. Важное значение в реализации воспитательных целей обучения математике имеет исторический материал, который позволяет в доступной для учащихся форме раскрыть основу происхождения математических понятий и фактов. Он воспитывает и развивает интеллект. Незаменимым средством при этом являются также старинные задачи, математические игры и т.п. Развивающие (мировоззренческие) цели: формирование мировоззрения учащихся, логической и эвристической составляющих мышления, алгоритмического мышления; развитие пространственного воображения. Развивающие цели должны находиться также в тесной связи с содержанием урока. В качестве примера, развивающими целями обучения математике могут быть: развитие у обучающихся навыков применения в процессе изучения математики научных методов (анализа, синтеза, сравнения, аналогии, индукции, дедукции, обобщения, конкретизации, моделирования классификации); развитие у учащихся геометрической, алгебраической и числовой интуиции, пространственного воображения, наблюдательности, памяти и др. Цели обучения могут формулироваться по-разному в зависимости от их ориентации. Например, можно определить цель обучения через деятельность учителя; через учебную деятельность учащихся. Требования к целям: а) образовательные цели должны обладать конкретностью, конструктивностью, проверяемостью, участием ученика в процессе учения; б) воспитательные цели должны пронизывать весь учебный процесс, выражать стремление к аргументации и четким логическим схемам рассуждения; в) личностно-ориентированные цели должны учитывать формирование возможных в том или ином возрасте качеств личности средствами предмета математики. Формирование действия целеполагания у обучающихся происходит в несколько этапов: 1) учитель раскрывает структуру действия постановки (полагания) цели; 2) учитель привлекает детей к постановке цели и критическому осмыслению полученных результатов при достижении цели; 3) учащиеся под руководством учителя конструируют цель изучения конкретного учебного материала; 4) учащиеся самостоятельно ставят цели, а классный коллектив критически анализирует процедуру постановки цели и достижения результата. Цели, содержание и методы обучения взаимно связаны и обусловливают друг друга (при сохранении ведущей роли целей обучения). Из различных целей обучения наиболее подвижны и изменчивы образовательные цели. Достижение целей обучения математике определяется функциями обучения математике. ФУНКЦИИ ОБУЧЕНИЯ МАТЕМАТИКЕФункции обучения математике: образовательная, воспитательная и развивающая, а также: эвристическая, прогностическая, эстетическая, практическая, контрольно-оценочная, информационная, корректирующая и интегрирующая. Образовательная функция обучения предполагает овладение школьниками системой математических знаний, дающей представление о предмете математики, ее методах и приложениях. Образовательная функция во многом обусловливает развитие мировоззрения школьников, которое представляет собой синтез знаний, умений и убеждений. Воспитательная функция характеризуется формированием интереса к изучению математики, развитием устойчивой мотивации к учебной деятельности. Развивающая функцияобучения заключается в формировании познавательных психических процессов и свойств личности, таких как внимание, память, мышление, познавательная активность и самостятельность, способности, а также формирование логических приемов мыслительной деятельности (анализа, синтеза, обобщения, абстрагирования и т.п.), общеучебных приемов. Информационная функция заключается в том, что в процессе обучения ученик знакомится с историей возникновения математических идей, их развитием, биографией ученых, разными точками зрения на те или иные концепции. В процессе обучения математике ученик получает достаточно большой объем информации, знакомится с различными приложениями математики, новыми открытиями в области математики. Эвристическая функция обучения предполагает создание учителем в процессе обучения условий, которые обеспечивают развитие способностей ребенка. К эвристической функции обучения относится применение учителем эвристических приемов и методов в обучении математике, умение применять их в различных конкретных ситуациях. Прогностическая функцияобучения математике ориентирована на формирование у школьников прогностических умений: умение обнаруживать нерешенные проблемы, выдвигать гипотезы, умение видеть альтернативное решение проблем и др. Эстетическая функцияпредусматривает приобщение школьников к красоте, воспитание у них эстетических вкусов. Учебный материал должен быть изложен логически последовательно, системно и привлекательно. Практическая функция обучения математике заключается в ориентации обучения на решение задач, на формирование умения математически исследовать явления реального мира, на практическую направленность учебного материала. Изначальным стимулом развития математического знания является потребность в решении конкретных практических задач. Движение вперед в области математики обусловлено возникновением потребностей, в большей или меньшей мере носящих практический характер. Но, раз возникшее, оно неизбежно приобретает внутренний размах и выходит за рамки непосредственной полезности, отмечает Р. Курант. Контрольно-оценочная функция обучения математике заключается в необходимости осуществления контроля, коррекции, оценки знаний и умений школьников. Сегодня в школах распространено тестирование. Корректирующая функция заключается в корректировании информации, получаемой учащимися. Значение и сущность информации, полученной из различных источников, может быть различной. Учитель должен предлагать учащимся откорректированную информацию. Он должен помочь ученику правильно разобраться в ней и оценить ее. Интегрирующая функция заключается в формировании системности знаний, в понимании взаимосвязи между изучаемыми понятиями, теоремами, способами деятельности, методами. Все функции обучения математике взаимосвязаны, они зависят друг от друга и реализуются на практике в различных сочетаниях. Обучение математике, реализуя свои функции, обеспечивает достижение основных целей обучения. Перечисленные выше цели математического образования составляют основу отбора его содержания. ГУМАНИЗАЦИЯ И ГУМАНИТАРИЗАЦИЯ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ Гуманизацияобразования предполагает «очеловечивание» знания, необходимость дифференциации и индивидуализации обучения. Гуманизация математического образования это, прежде всего воспитание четких представлений об этических нормах и осознание невозможности отступления от них. Появление различных типов школ, классов с углубленным изучением математики представляют собой проявления гуманизации образования. Появилась необходимость новых подходов в осмыслении проблем целей, содержания, форм, методов и средств обучения математике в школе, её места и роли в системе школьных предметов. Гуманитаризация (лат. «humanitas» - человеческая природа, духовная культура) математического образования проявляется в приобщении школьников к духовной культуре, истории развития науки, творческой деятельности, что в конечном счете реализуется в увеличении числа часов в учебных планах на изучение гуманитарных дисциплин. Гуманитарная составляющая математического образования определяется отношением к человеку, его общественному бытию и сознанию. Говоря о «гуманитарной математике», подразумевается связь математики с гуманитарными науками, а также материальными и духовными общественными отношениями. С этих позиций наиболее важными являются: методологические вопросы математики как метода познания природы и общества; философские проблемы математики, показывающие ее роль в обществе; связь математики с другими науками; связи математики с производством, ее роль в управлении, быту, трудовом воспитании; связь математики с духовной культурой, развитие мышления, политическое, нравственное и эстетическое воспитание; вклад математического образования в формирование научного гуманистического мировоззрения учащихся. С целью гуманитаризации математического образования необходимо прежде всего внести в традиционный школьный курс математики разнообразные формы, методы и стили, свойственные гуманитарным дисциплинам. Это можно осуществить через освобождение школьного математического курса от технически сложных вопросов, доказательств теорем, усиливая прикладную направленность дисциплины, раскрывая смысл математического моделирования, показывая значимую роль математики в развитии культуры и общества. Математика наука гуманитарная. Именно математика лежит в основе всех наук. Она имеет свой язык, свою лексику, грамматику. Математические идеи, методы постепенно проникают в самые традиционные гуманитарные науки, прививая им строгий стиль мышления. Математика развивает образное мышление, так как представляет собой источник образов. «Образность» мышления очень важна для людей с гуманитарными интересами. Уметь видеть разнообразные формы в их пространственном и плоскостном изображении, распознавать конфигурации, представлять себе вид графика функции, зная ее свойства, все это способствует развитию логического мышления, пространственного воображения, эстетического чувства, ассоциативного мышления, помогает почувствовать целостность изучаемых объектов и понимать простые геометрические факты и ситуации. Гуманитарное преподавание математики немыслимо без изучения ее истории. Это не только краткие биографические сведения о выдающихся математиках, но и история возникновения и развития математических идей. Уместно вспомнить о замечательных гуманитариях, которые любили математику и хорошо её знали, о математиках, внесших вклад в развитие гуманитарных наук. Таким образом, элементы истории должны органично входить в курс математики в гуманитарной школе. Математика позволяет воспитывать чувство прекрасного, совершенного, учит видеть и понимать окружающий нас мир, его красоту и внутреннюю гармонию. Математика оказывает существенное влияние на эстетические вкусы и взгляды учащихся. Гуманизация и гуманитаризация обучения математике предполагают особые отношения между учителем и учеником, в ходе которых происходит вовлечение школьников в содержание учебного процесса; используются диалогические приемы общения между учителем и учащимися; реализуются творческие начала каждого школьника. СОДЕРЖАНИЕ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ. ОСНОВНЫЕ СОДЕРЖАТЕЛЬНО-МЕТОДИЧЕСКИЕ ЛИНИИ ШКОЛЬНОГО КУРСА МАТЕМАТИКИ Содержание математического школьного образования отражается в ряде нормативных документов, учебниках, учебных планах, учебных программах, методических пособиях. Учебные программы по математике включают в себя перечень тем изучаемого материала, рекомендации по количеству времени на каждую тему, перечень знаний, умений и навыков по предмету. Расположение математического материала в учебных программах осуществляется в трех вариантах: линейное (материал располагается последовательно); концентрическое (некоторые разделы изучаются с повтором на новом уровне); спиральное (материал располагается последовательно по циклам). Cодержание математического образования включает: систему знаний об окружающем нас мире; систему общих интеллектуальных и практических навыков и умений; опыт творческой деятельности, ее основные черты, которые постепенно были накоплены человечеством в процессе развития общественно-практической деятельности; опыт эмоционально-волевого отношения к миру, обществу, друг к другу. Новые научные достижения в области математики, их внедрение в практику приводят к пересмотру школьного курса математики, обогащению его новыми приложениями. Одновременно из содержания школьного образования исключаются или сокращаются до минимума разделы, не актуальные и потерявшие свою практическую значимость. На смену приходят вопросы, имеющие важное значение в современном образовании. Содержание образования строится с учетом факторов, детерминирующих на современном этапе развития общества. Таковыми сегодня являются: соответствие логике математики как науки; степень его удовлетворения принципам обучения (научности, последовательности, системности и т.д.): учет психологических возможностей и возрастных особенностей школьников разных ступеней обучения (младший, средний, старший школьник); потребности личности в образовании (дифференцированное обучение, коррекционное обучение и т.д.); формирование профессиональной направленности школьников. Анализируя школьные программы по математике, начиная с 70-х годов прошлого ХХ века, можно во всех или некоторых из них вычленить следующие содержательно-методические линии: числовая (арифметические операции в различных числовых множествах); используется вычислительный метод; линия выражений и тождественных преобразований, использующая метод тождественных преобразований; функциональная линия, использующая метод исследования функций, функциональный метод решения уравнений и неравенств, координатный метод; линия уравнений и неравенств, использующая метод уравнений и неравенств при решении задач (метод моделирования); обобщенные методы решения уравнений и неравенств 5) линия геометрических фигур, использующая метод цепочки треугольников, метод геометрических мест точек (пересечения фигур); 6) линия геометрических величин, использующая метод исчерпывания (интегрального исчисления), методы «разрезания», дополнения и «перекраивания» фигур; методы площадей и объемов; 7) векторно-координатная линия, использующая векторный метод, координатный метод; 8) линия геометрических преобразований, использующая метод геометрических преобразований. Ведущие содержательные линии обеспечивают целостное восприятие курса математики за счет реализации многочисленных связей внутри и вне материала, относящегося к той или иной линии, и раскрытия базисных для школьного курса математики. Математические методы вводятся в содержание обучения и применяются в разных темах и разделах школьной математики, обеспечивая реализацию какой-то из фундаментальных математических идей и выступая как основное средство установления внутрипредметных математических связей. ? Вопросы для самопроверки:Охарактеризуйте роль математического образования в развитии личности. Какие принципы лежат в основе перестройки системы математического образования? Охарактеризуйте цели обучения математике. Как соотносятся цели образования и цели обучения математике? Какие уровни обучения математике выделяются? Охарактеризуйте функции обучения математике. Раскройте содержание понятий «гуманизация» и «гуманитаризация» математического образования. Назовите компоненты содержания математического образования, раскройте их содержание. Охарактеризуйте варианты расположения математического материала в учебных программах по математике. Приведите примеры. Что является основой проектирования содержания образования учебного предмета математики? Каким основным задачам должно отвечать содержание образования математике? |
