стальной каркас. КП МК Стальной каркас одноэтажного производственного здания ПЗ. Стальной каркас одноэтажного производственного здания

• Название: Стальной каркас одноэтажного производственного здания
• Анкор: стальной каркас
• Дата: 13.06.2022
• Размер: 6.69 Mb.
• Имя файла: КП МК Стальной каркас одноэтажного производственного здания ПЗ .doc
• Тип: Пояснительная записка; #587882
• страница: 5 из 9

3.4. Подбор сечения стержней фермы

Стержни стропильных ферм выполнены из прокатных уголков сечениями, показанными на рисунке 13.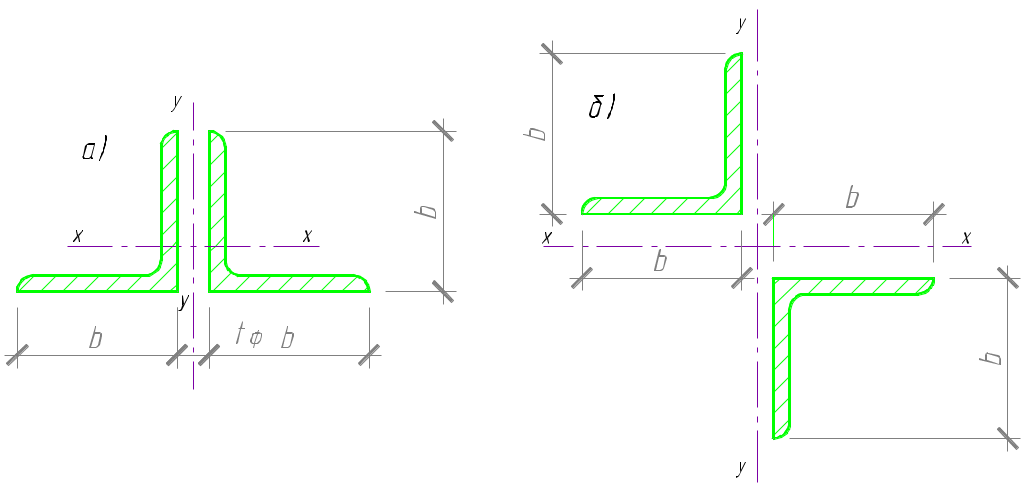

Рисунок 13. Сечения элементов легких ферм – равнополочные уголки (б – стержень 6-7, а- остальные стержни фермы)

Для изготовления фермы принимаем сталь марки С245 с расчетным сопротивлением на растяжение и сжатие R_y=240 МПа.

Подбор сечения стержней фермы выполним из условия прочности (для центрально-растянутых элементов) и условия устойчивости (для сжатых элементов):

а) Условие прочности центрально-растянутого элемента:

σ=N/A_n≤R_y*_с,

где: N – расчетное усилие в рассматриваемом стержне;

R_y – расчетное сопротивление материала;

А_n – площадь сечения стержня нетто;

_с – коэффициент условий работы, _с=1 (для растянутых элементов).

Требуемая площадь центрально-растянутого элемента из условия прочности:

A_n^тр≥N/R_y

Далее подбираем равнополочные уголки по ГОСТ 8509-93.

б) Условие устойчивости центрально-сжатого стержня:

σ=N/(φ*A)≤R_y*_с,

где: А – площадь сечения элементов брутто;

 – коэффициент продольного изгиба, который зависит от гибкости стержня .

Коэффициент условия работы учитывают для тех стержней решетки, которые получаются с небольшим сечением гибкостью   60 и которые могут легко деформироваться во время изготовления, транспортирования и монтажа фермы. Следовательно, для сжатых раскосов (кроме опорного) и стоек при   60 _с=0,8.

Требуемая площадь центрально-сжатого стержня из условия устойчивости:

A^тр≥N/(φ*_с*R_y)

т.к. коэффициент  в неявном виде зависит от площади сечения, то задачу решают методом последовательных приближений. В первом приближении задаемся: для поясов =80…100, для раскосов и стоек =100…120.

Определив  в зависимости от  и R_y вычисляем величину А^тр в первом приближении, из сортамента подбираем соответствующие профили уголков.

Необходима проверка принятого сечения по условию устойчивости: сжатый стержень потеряет устойчивость в той плоскости, относительно которой гибкость максимальная, т.к. при этом  минимальный. Поэтому вычисляем гибкости _x и _y:

_x=l_ef^x/r_x,

_y=l_ef^у/r_x,

где l_ef^x – расчетная длина сжатого стержня в плоскости фермы;

l_ef^у – то же, из плоскости фермы;

r_x, r_y – радиусы инерции сечения относительно осей х и у.

Для верхнего пояса расчетная длина стержня:

l_ef^x=l,

где l – расстояние между центрами узлов.

Расчетная длина опорного раскоса:

l_ef^x=0,5*l.

Для остальных сжатых стержней раскосов и стоек вводится коэффициент опорного защемления =0.8, так что расчетная длина будет:

l_ef^x=0,8*l,

Для определения расчетных длин сжатых стержней из плоскости фермы рассматривается схема связей по верхним поясам ферм.

Связи по верхним поясам ферм уменьшают расстояние между узлами, закрепленными от горизонтального смещения, поэтому:

l_ef^у=l_закр,

где l_закр – расстояние между закрепленными от горизонтального смещения точками (при беспрогонной системе покрытия l_закр равно шагу узлов фермы верхнего пояса).

Для сжатых раскосов и стоек расчетная длина при расчете устойчивости из плоскости фермы принимается по формуле l_ef^x=l.

Слабозагруженные сжатые стержни решетки рассчитываются по предельной гибкости, а сечения подбирают по требуемому радиусу инерции:

r_min^тр=l_ef^у/_пр.

Предельная гибкость:

- для сжатых стержней поясов и опорных раскосов: _пр=180-60*α;

- для сжатых стержней раскосов и стоек: _пр=210-60*α;

- для растянутых стержней: _пр=400,

где α=N/(φ_min*A*R_y*_с)≥0.5.

Толщину фасонок назначаем конструктивно, исходя из величины усилий в опорном раскосе: при N=-406.05принимаем толщину фасонки t_ф=12 мм.

Во избежание повреждения при транспортировке и монтаже наименьший уголок принимается с размерами 50х5 мм.

Все расчеты сведены в таблицу 5.

Таблица 5

Таблица подбора сечений стержней ферм

(толщина фасонки t_ф=12 мм, уклон i=0, сталь С245, R_y=240 МПа)

Элемент	Обозначение стержня	Расчетное усилие	Сечение, мм		Площадь сечения, см2	Геометрическая длина, мм	Расчетная длина, см		Радиусы инерции, см		Гибкости		Предельная гибкость	Коэф. продольного изгиба	Коэф. условий работы	Расчетное напряжение, МПа	Недонапряжение, %
-	-	N	b	t	А	l	lxеf	lуеf	rx	ry	x	y	пр	min	c	σ	∆
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
ВП	В-1	245.07	125	9	43.9	2800	280	280.0	3.81	5.63	73.4	49.7	400	-	0.95	55.9	308.2
	Г-3, Д-4	-460.43	125	9	43.9	3000	300	300	3.81	5.63	78.7	53.3	140	0.696	0.95	-150.8	51.2
	Е-6	-620.07	125	9	43.9	3000	300	300	3.81	5.63	78.7	53.3	127	0.696	0.95	-203.1	12.2
НП	А-2	258.78	100	7	27.3	5800	580	580	3.05	4.56	190.2	127.2	400	-	0.95	94.8	140.5
	А-5	582.26	100	7	27.3	6000	600	600	3.05	4.56	196.7	131.6	400	-	0.95	213.3	6.9
Раскосы	1-2	-406.03	110	8	34.3	4220	211	422	3.36	4.99	62.9	84.6	123	0.651	0.8	-181.7	5.6
	2-3	311.68	63	6	14.7	4250	425	425	1.92	2.97	221.2	143.2	400	-	0.95	211.4	7.8
	4-5	-199.23	100	7	27.3	4360	348.8	436	3.05	4.56	114.4	95.7	160	0.452	0.8	-161.6	18.8
	5-6	85.33	50	5	9.8	4250	425	425	1.53	2.41	278.7	176.5	400	-	0.95	87.5	160.5
Стойки	3-4	-84.02	63	6	14.7	3090	247.2	309	1.92	2.97	128.6	104.1	162	0.371	0.8	-153.4	25.1
	6-7	-84.02	63	6	14.7	3090	247.2	309	2.97	2.97	83.3	104.1	175	0.515	0.8	-110.6	73.6

Для ферм пролетом 24 м оптимальное количество типоразмеров - 4…5, и сечения поясов не меняют, поэтому окончательно принимаем:

В-1, Г-3, Д-4, Е-6 – ∟125х9;

1-2 – ∟110х8;

А-2, А-5, 4-5 – ∟100х7;

2-3, 3-4, 6-7 – ∟63х6;

А-1, 5-6 – ∟50х5.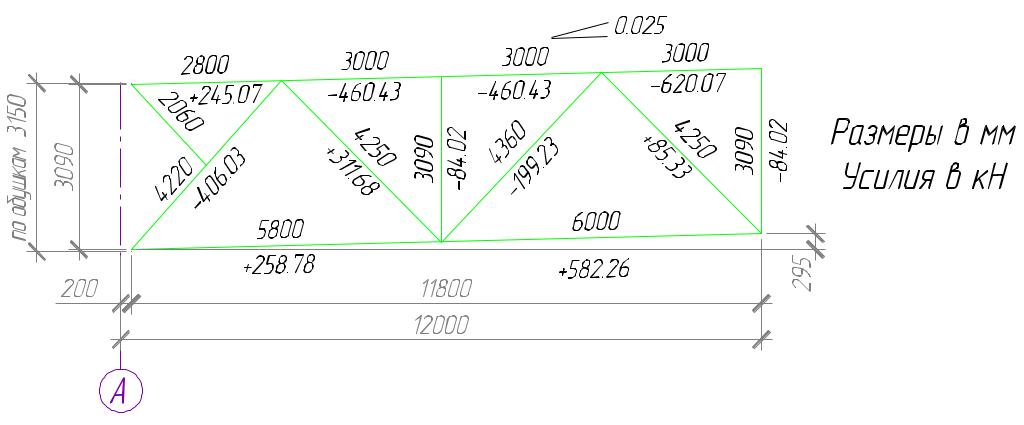

Рисунок 14. Геометрическая схема полуфермы