стальной каркас. КП МК Стальной каркас одноэтажного производственного здания ПЗ. Стальной каркас одноэтажного производственного здания

Название	Стальной каркас одноэтажного производственного здания
Анкор	стальной каркас
Дата	13.06.2022
Размер	6.69 Mb.
Формат файла
Имя файла	КП МК Стальной каркас одноэтажного производственного здания ПЗ .doc
Тип	Пояснительная записка #587882
страница	7 из 9

1 2 3 4 5 6 7 8 9

4. Расчет и конструирование ступенчатой колонны

4.1. Исходные данные для расчета ступенчатой колонны

Расчет и конструирование ступенчатой колонны

Рассчитываем ступенчатую колонну со сплошным сечением в верхней части и сквозным в нижней (ригель имеет жесткое сопряжение с колонной).

Расчетные усилия (расчетные сечения колонны изображены на рисунке 10):

- для верхней части колонны:

в сечении 1-1 М₁=-765.853 кН*м; N₁=-646.32 кН; Q₁=-208.252 кН (загружение №№ 1, 2, 3, 5, 10);

в сечении 2-2 М₂=681.619 кН*м (загружение №№ 1, 2, 3, 5, 10),

- для нижней части колонны:

в сечении 3-3 М₃=-1986.137 кН*м; N₃=-3447.64 кН; Q₃=-179.857 кН (загружение №№ 1, 3, 6; изгибающий момент догружает подкрановую ветвь);

в сечении 4-4 М₄=2207.159 кН*м; N₄=-3377.461 кН; Q₄=-253.673 кН (загружение №№ 1, 2, 3, 6, 10; изгибающий момент догружает наружную ветвь),

Q_max=-255.874 кН.

Соотношение жесткостей верхней и нижней части колонны I_B/I_H=0.1.

Материал колонны – сталь марки С245 (R_y=240 МПа), бетон фундамента марки В15 (R_b=8.5 МПа).

4.2. Определение расчетных длин колонны

Так как H_в/H_н=l₂/l₁=7200/17200=0.42<0.6, N_н/N_в=3447.64/646.32=5.3>3 и в однопролетной раме с жестким сопряжением ригеля с колонной верхний конец последней закреплен только от поворота, то для нижней части колонны μ₁=2, для верхней - μ₂=3.

Расчетные длины для нижней и верхней частей колонны в плоскости рамы:

l_x1=μ₁*l₁,

l_x2=μ₂*l₂.

l_x1=2*17200=34400 мм,

l_x2=3*7200=21600 мм.

Расчетные длины для нижней и верхней частей колонны из плоскости рамы:

l_y1=Н_н,

l_y2=Н_в-h_п.б.

l_y1=17200 мм,

l_y2=7200-1800=5400 мм.

4.3. Подбор сечения верхней части колонны

4.3.1. Выбор типа сечения верхней части колонны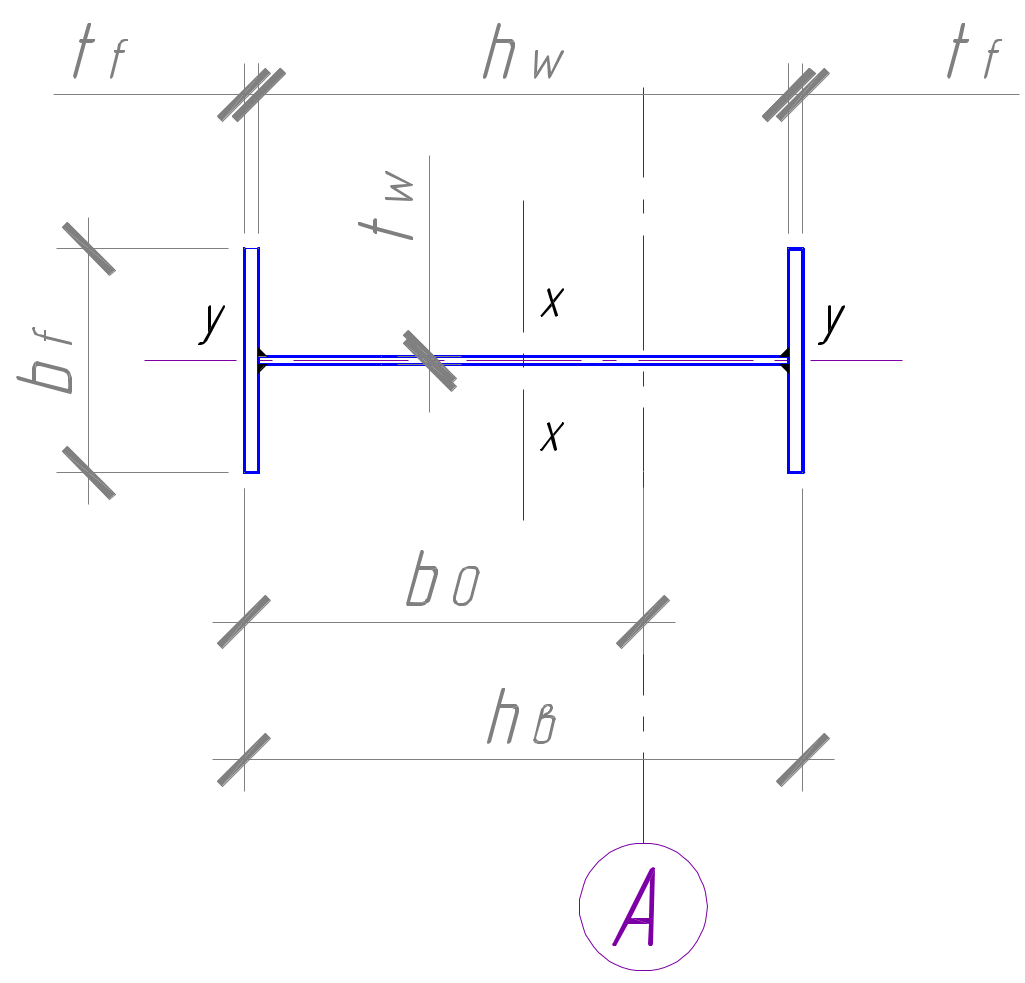

ечение верхней части колонны принимаем в виде сварного двутавра высотой h_в=700 мм (рисунок 20).

Для симметричного двутавра:

i_x≈0,42*h_в,

ρ_х≈0,35*h_в.

i_x≈0,42*700=294 мм;

ρ_х≈0,35*700=245 мм.

Условная гибкость:

=(l_x₂/i_x)*(R_y/E)^0.5,

=(21600/294)*(240/206000)^0.5=2.51. Рисунок 20. Сечения верхней части колонны

Относительный эксцентриситет:

m_x=e_x/ρ_x=M₁/(N₁*ρ_x),

m_x=765.853*10³/(646.32*245)=4.84.

Примем в первом приближении А_f/А_w=1, тогда коэффициент влияния формы сечения:

η=(1.90-0.1*m_x)-0.02*(6-m_x)*

,

η=(1.90-0.1*4.84)-0.02*(6-4.84)*2.51=1.36.

Приведенный относительный эксцентриситет:

m_x_ef=η*m_x,

m_x_ef=1.36*4.84=6.57.

По таблице 74 СНиП II-23-81* находим φ_е=0.168.

Требуемая площадь сечения надкрановой части колонны:

А_тр=N₁/(φ_е*R_y),

А_тр=646.32*10³/(0.168*240)=16030 мм².

Компоновка сечения.

Принимаем толщину полок t_f=18 мм.

Высота стенки:

h_w=h_в-2*t_f,

h_w=700-2*18=664 мм.

Условие местной устойчивости стенки при

>0.8 и m_x>1:

h_w/t_w≤(0.36+0.8*

)*(E/R_y)^0.5,

h_w/t_w≤(0.36+0.8*2.51)*(206000/240)^0.5=69.3,

t_w≥h_w/69.3=664/69.3=9.6 мм.

Принимаем толщину стенки t_w=10 мм.

Требуемая площадь полки:

А_f._тр=(А_тр-t_w*h_w)/2,

А_f._тр=(16030-10*664)/2=4695 мм².

Задаемся шириной полки из условия устойчивости верхней части колонны из плоскости действия момента:

b_f≥l_y2/20,

b_f≥5400/20=270 мм, примем b_f=280 мм.

Условие местной устойчивости полки:

b_св/t_f≤(0.36+0.1*

)*(E/R_y)^0.5,

где b_св=(b_f-t_w)/2=(280-10)/2=135, тогда

b_св/t_f≤(0.36+0.1*2.51)*(206000/240)^0.5=17.9, тогда

t_f≥b_св/17.9=135/17.9=7.5 мм.

Принимаем сечение надкрановй части колонны – сварной двутавр с размерами:

b_f=280 мм;

t_f=18 мм;

А_f=280*18=5040 мм²>А_f.тр=4695 мм²;

h_w=664 мм;

t_w=10 мм;

А_w=664*10=6640 мм².

Геометрические характеристики сечения.

Полная площадь сечения:

А₀=2*А_f+А_w,

А₀=2*5040+6640=16720 мм².

Моменты инерции сечения относительно осей х и y:

I_x=t_w*h_w³/12+2*b_f*t_f*[(h_в-t_f)/2]²,

I_y=2*t_f*b_f³/12.

I_x=10*664³/12+2*280*18*[(700-18)/2]²=1416074933 мм⁴,

I_y=2*18*280³/12=65856000 мм⁴.

Момент сопротивления сечения относительно оси х:

W_x=I_x/(0.5*h_в),

W_x=1416074933/(0.5*700)=4045928 мм³.

ρ_x=W_x/А₀=4045928/16720=242 мм.

Радиусы инерции сечения относительно осeй х и y:

i_x=(I_x/А₀)^0,5,

i_y=(I_y/А₀)^0,5.

i_x=(1416074933/16720)^0,5=291 мм,

i_y=(65856000/16720)^0,5=63 мм.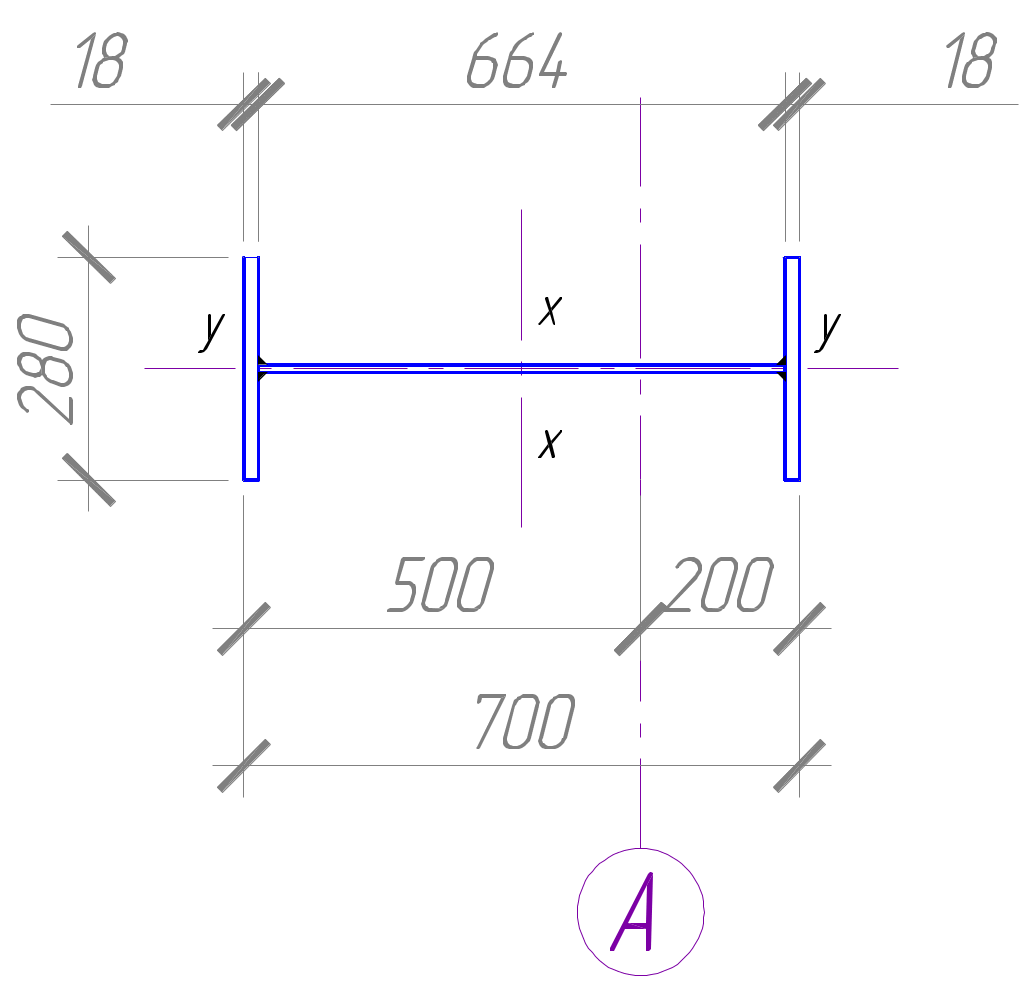

Рисунок 21. Сечение верхней части колонны

4.3.2. Проверка устойчивости верхней части колонны

Проверка устойчивости верхней части колонны в плоскости действия момента.

Расчет на устойчивость внецентренно-сжатого элемента постоянного сечения в плоскости действия момента выполняем по формуле:

N₁/(φ_e*A₀)≤R_y*γ_c,

φ_e – коэффициент определяемый по табл. 74 СНиП II-23-81* и зависящий от условной гибкости

=λ_x*(R_y/E)^0.5 и приведенного относительного эксцентриситета m_еf определяемого по формуле:

m_ef_x=η*m_x,

где η – коэффициент влияния формы сечения, определяемый по табл. 73 СНиП II-23-81*,

m_x=M_x/(N₁*ρ_x) – относительный эксцентриситет.

λ_x=l_x₂/i_x=21600/291=74.2.

=74.2*(240/206000)^0.5=2.53, 0<

<5

m_x=765.853*10³/(646.32*242)=4.90.

А_f/А_w=5040/6640=0.76≈0.5.

Коэффициент влияния формы сечения:

η=(1,75-0,1*m_x)-0,02*(5-m_x)*

,

η=(1,75-0,1*4.90)-0,02*(5-4.90)*2.53=1.26.

m_ef_x=1.26*4.90=6.15.

По таблице 74 СНиП II-23-81* находим φ_e=0.173.

σ=646.32/(0.173*240)=223.4 МПа < R_y=240 МПа.

Недонапряжение:

∆=100*(240-223.4)/240=6.9 %.

Проверка устойчивости верхней части колонны из плоскости действия момента.

Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения из плоскости действия момента выполняем по формуле:

N₁/(с*φ_y*A₀)≤R_y*γ_c,

где φ_y – коэффициент определяемый по табл. 72 СНиП II-23-81*.

Определим коэффициенты с и φ_y_.

λ_y=l_y₂/i_y=5400/63=86, по табл. 72 СНиП II-23-81* находим φ_y=0.640.

Максимальный момент в средней трети расчетной длины стержня:

M_x^1/3=M₂+(l₂-l_y₂/3)*(M₁-M₂)/l₂,

M_x^1/3=681.619+(7200-5400/3)*(-765.853-681.619)/7200=-404 кН*м.

IM_x^1/3I>IМ_max/2I=766/2=383 кН*м.

Относительный эксцентриситет:

m_x=M_x^1/3*A₀/(N₁*W_x),

m_x=-404*16720/(646.32*4045928)=2.58.

При m_x<5 коэффициент с, учитывающий влияние момента М_х при изгибно-крутильной форме, вычисляется по формуле:

с=β/(1+α*m_x),

λ_y=86<λ_с=3.14*(E/R_y)^0.5=3.14*(206000/240)^0.5=92 => β=1,

m_x=2.58>1 => α=0,65+0,05*m_x=0,65+0,05*2.58=0.78.

c=1/(1+0.78*2.58)=0.33.

Поскольку h_w/t_w=664/10=66.4<3.8*(E/R_y)^0.5=3,8*(206000/240)^0.5=111, то A_расч=16720 мм².

σ=646.32/(0.33*0.640*16720)=182 МПа < R_y=240 МПа

Недонапряжение:

∆=100*(240-182)/240=24.2 %.

1 2 3 4 5 6 7 8 9