Нечеткая логика на практике. Статья о нечеткой логике обычно грешит двумя вещами
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
6. Заключение— Классифицируемая как техника с искусственным интеллектом, нечеткая логика используется для моделирования и замещения опыта управления процессом и опыта разработчиков и операторов. — Как средство повышения качества и производительности, нечеткая логика предлагает преимущества повышения конкурентоспособности производственным компаниям в поисках технико-экономической оптимизации. — В данном документе определены области, в которых данный подход может быть использован наиболее эффективно. — Благодаря удобному пользовательскому интерфейсу среды программирования ПЛК, нечеткая логика доступна всем инженерам, занимающимся автоматическим управлением, которые хотят повысить уровень своих навыков и знаний, а также эксплуатационные характеристики своих разработок. Такой инструментарий имеется в наличии в среде программирования для некоторых контроллеров (см. рис. 30). — Конкуренция с другими традиционными средствами управления (например, ПИД-контроллеры) вызывает развитие в большинстве областей применения. — Нечеткая логика имеет свои специальные области, в которых превосходно работает: это области, где важен практический опыт, нюансы при принятии решений и учет нелинейных и субъективных параметров, не говоря уже о противоречащих друг другу факторах принятия решения. Контакт со специалистами компании Schneider поможет пользователям и разработчикам найти подходящее решение для ответа на их закономерных вопрос: “Какие несомненные преимущества может внести нечеткая логика в мое приложение?” 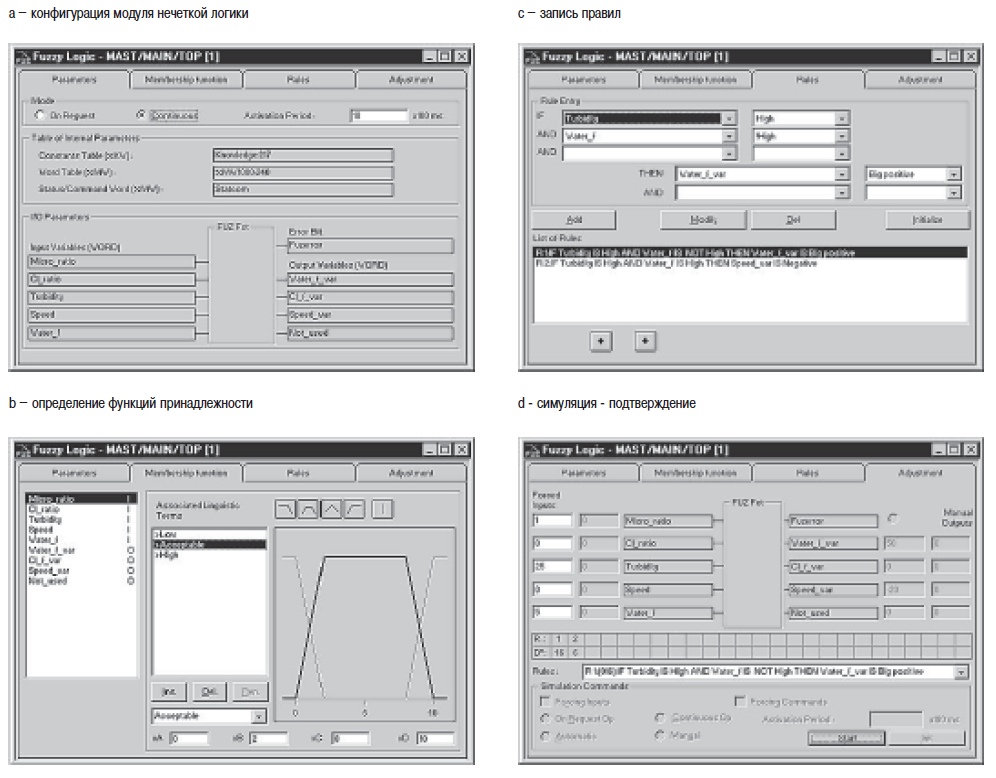 Рис. 30. ПЛК компании Schneider имеют в среде программирования на ПК дружественный пользовательский интерфейс для конфигурирования нечеткой логики ПриложениеОперации между нечеткими множествами В таблице на рис. 31 представлены операторы Заде. 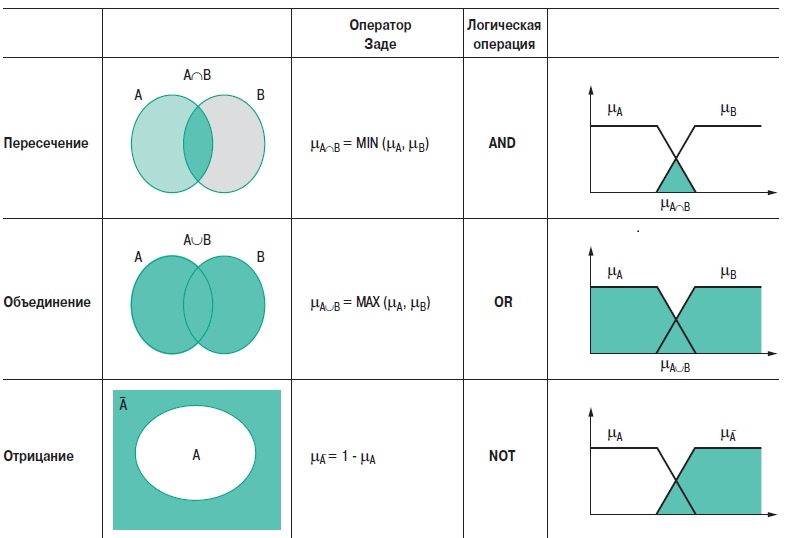 Рис. 31. Операции между нечеткими множествами Функции принадлежности одноэлементного множества Функции принадлежности одноэлементного множества часто используются в качестве выходных фунций правил нечеткой логики. Поскольку они допускают производить интерполяцию между правилами как для функций принадлежности треугольной формы (к примеру), дальнейшие вычисления упрощаются. Нет необходимости в вычислении максимума выходной функции принадлежности (агрегация) и поиск центра тяжести также упрощается. На рис. 32 представлен такой пример. 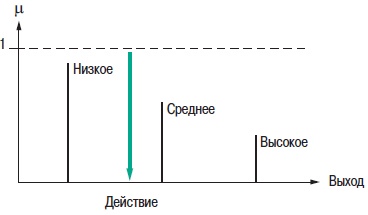 Рис. 32. Дефаззификация функции принадлежностиодноэлементного множества Нечеткий логический вывод: нечеткий вывод и обобщенное правило дедукции (Generalised Modus Ponens) Как показано на рис. 33, традиционный, направленный вперед механизм логического вывода “начиная с фронта” или “modus ponens” заключается в использовании правил, также известных как выводы, и механизма дедукции (modus ponens) для того, чтобы получить результат на основании имеющихся фактов. 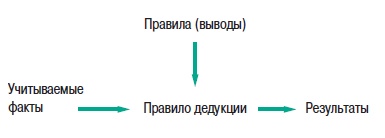 Рис. 33. Принципы логического вывода «начиная с фронта» Вывод “A ⇒ B” считается истинным до тех пор, пока не становится недействительным (A истинно и B ложно): см. рис. 34. Если есть информация, где вывод является истинным, а где ложным, то по правилу дедукции можно получить результат B’ при анализе A’. 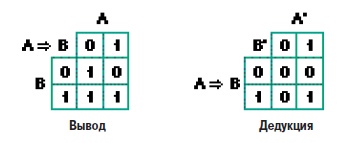 Рис. 34. Принцип вывода и правила дедукции Аналогичный теоретический принцип можно распространить в нечеткой логике. Общая диаграмма приведена на рис. 35.  Рис. 35. Принцип нечеткого логического вывода Механизм обобщения вывода также известен как “нечеткий вывод”. Существует несколько операторов нечеткого вывода, включая перечисленные ниже: Оператор МАМДАНИ: μA⇒B = MIN (μA, μB) Оператор ЛАРСЕНА: μA⇒B = μA . μB Оператор ЛУКАСЕВИЧА: μA⇒B = MIN (1,1 - μA + μB) Нечеткий вывод работает аналогично традиционному, при этом A и B представляют собой нечеткие множества. Механизм, основанный на обобщенном правиле дедукции, подчиняется следующей формуле и используется для определения вывода нечеткого множества B’. Чаще всего применяется оператор T: Минимум (также известный как оператор Заде). μB’(y) = MAXx (T(μA’(x), μA⇒B (x,y)) ) где T: оператор правила дедукции (t - стандартный). Поведение оператора Лукасевича аналогично поведению традиционного вывода, когда мы ограничиваемся только булевыми переменными. Этот случай не подходит для операторов Ларсена и операторов Мамдани, которые используются в базах правил Мамдани. Такие операторы чаще всего используются поскольку: — они имеют высокую степень устойчивости в приложениях. — значительно упрощаются вычисления и графическая интерпретация (см. секцию 2.4). Вычисления по входу x и выходу y производятся по формулам, приведенным ниже: μB’(y) = MAXx (Min (μA’ (x), μA(x), μB(y)) ) = Min (μB(y), MAXx (Min (μA’(x), μA(x)) ) БиблиографияСтандарты МЭК 61131-7: Программируемые контроллеры часть 7 Программирование нечеткого управления. Разнообразныеработы Fuzzy models for pattern recognition. IEEE Press, 1992. James C. BEZDEK & Sanker K. PAL. Fuzzy sets and systems: Theory and applications. Academic Press 1980, Mathematics in Sciences and Engineering vol. 144. D. DUBOIS, H. PRADE. Evaluation subjective ; méthodes, applications et enjeux. es cahiers des clubs CRIN, club CRIN logique floue. A.I. and expert system myths, legends and facts. IEEE Expert 02/90, pp 8-20, 29 réf. M.S. FOX. La logique floue et ses applications. Addison-Wesley, 1995. Bernadette BOUCHON-MEUNIER. Internet http://www-isis.ecs.soton.ac.uk/research/nfinfo/fuzzy.html http://www.ortech-engr.com/fuzzy/reservoir.html |
