Нечеткая логика на практике. Статья о нечеткой логике обычно грешит двумя вещами

• Название: Статья о нечеткой логике обычно грешит двумя вещами
• Дата: 27.02.2023
• Размер: 2.11 Mb.
• Имя файла: Нечеткая логика на практике.docx
• Тип: Статья; #957319
• страница: 6 из 10

2. Теория нечетких множеств

2.1. Понятие частичной принадлежности к множеству

В теории множеств элемент либо принадлежит множеству, либо нет. Понятия множеств используется во многих математических теориях. Это важное понятие, однако, не рассматривает простые ситуации, когда не все ясно и понятно. Например при выборе фруктов очень не сложно определить общий набор яблок. Однако, при этом непросто определить набор спелых яблок. Мы понимаем, что яблоки созревают постепенно ... понятие набора спелых яблок, таким образом, является не четким (расплывчатым).

Понятие нечеткого множества было принято для того, чтобы учесть представленную выше ситуацию. Теория нечетких множеств базируется на понятии частичной принадлежности к множеству: каждый элемент принадлежит к нечеткому множеству немного или частично. Очертание нечеткого множества (см. рис. 1) не имеет “Явной” границы, а представляется “нечетким” или “размытым”.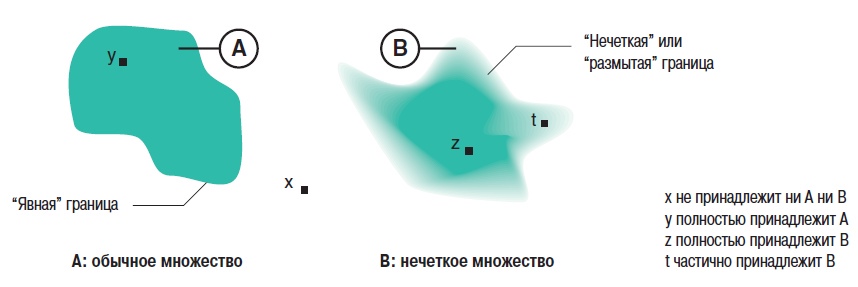



Рис. 1. Сравнение обычного и нечеткого множества

2.2. Функция принадлежности

Нечеткое множество определяется при помощи «функции принадлежности», которая соответствует понятию “характеристическая функция” в классической логике.

Предположим, мы хотим определить множество людей «среднего роста». В классической логике мы должны определить, что средним ростом мы считаем рост между 1,60 м и 1,80 м. Характеристическая функция в этом случае (см. рис. 2) дает “0” для всех, отличных от заданного диапазона ростов и “1” если рост соответствует заданному. Нечеткое множество людей «среднего роста» задается при помощи «функции принадлежности», которая в этом случае может принимать значения в диапазоне [0;1].

Каждый возможный рост в этом случае будет представлен в виде «функции принадлежности» к нечеткому множеству людей «среднего роста» (см. рис. 3), который принимает значения между 0 и 1.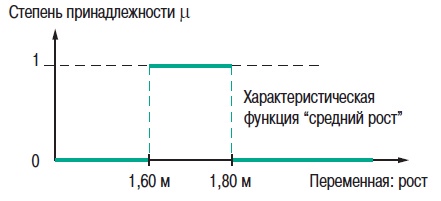



Рис. 2. Характеристическая функция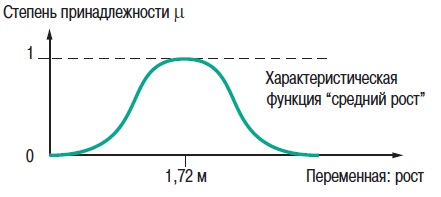



Рис. 3. Функция принадлежности

Несколько нечетких множеств можно определить через одну переменную, которая принимает нескольких значений, например множества “маленький рост”, “средний рост” и “высокий рост”. Каждое понятие описывает функция принадлежности (см. рис. 4).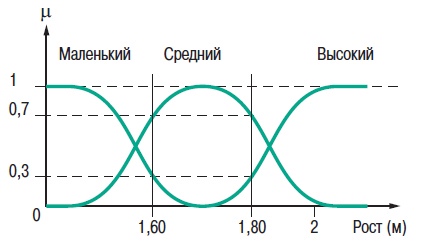



Рис. 4. Функция принадлежности, переменная и лингвистическоеописание

Этот пример показывает возможность применения нечеткой логики. Человека ростом 1,80 м можно отнести к группе “высокий рост” со степенью принадлежности 0,3 и к группе “средний рост” со степенью принадлежности 0,7. В классической логике переход от среднего роста к высокому мгновенен. Человек с ростом 1,80 м скорее всего принадлежит группе среднего роста, а человек ростом 1,81 м скорее всего высокий. Переменная (рост) и ее описания (средний, высокий), определенные функцией принадлежности, являются лингвистической переменной и лингвистическими описаниями соответственно.

Оба понятия лингвистическая переменная и лингвистическое описание могут быть напрямую использованы в правилах.

Функция принадлежности может принимать любую форму. Чаще для их представления используются кусочно-линейные линии (см. рис. 5).

Кусочно-линейные функции принадлежности обычно используется поскольку:

— они характеризуются простотой;

— они содержат точки, позволяющие задать области, где понятие является истинным, а где ложным, таким образом упрощает описание системы.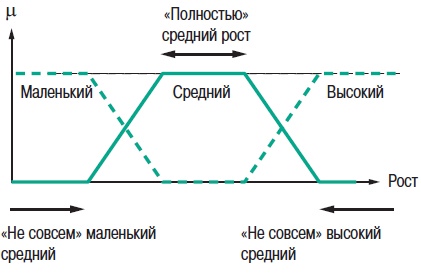



Рис. 5. Кусочно-линейная функция принадлежности

Далее в данном документе используются функции принадлежности этого типа.

Иногда функция принадлежности равна 1 для единственного значения переменной и 0 для всех других значений. В этом случае её называют функцией принадлежности одноэлементного множества. Ниже представлена (см. рис. 6) функция принадлежности одноэлементного множества переменной (рост), выраженной специфичным значением (рост Павла) данной переменной (подробная информация приведена в приложении).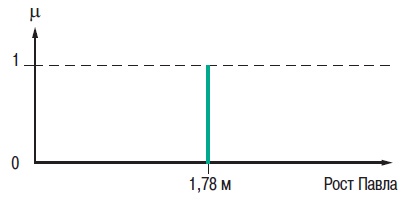



Рис. 6. Функция принадлежности одноэлементного множества

Подготовка задачи – определение степени принадлежности

Подготовка задачи для решения методами нечеткой логики (фаззификация) позволяет конвертировать реальные значения переменных в нечеткие.

Фаззификация заключается в определении степени принадлежности переменной (измерение, например) к нечеткому множеству. Например (см. рис. 7), если текущее значение «входной» переменной 2 то она принадлежит множеству “низкий уровень” со степенью принадлежности 0,4. Это и есть результат фаззификации.

Также можно сказать, что предположение “низкий уровень” является истинным при 0,4. При этом можно говорить о степени истинности предположения. Степень принадлежности и степень истинности, таким образом, являются схожими понятиями.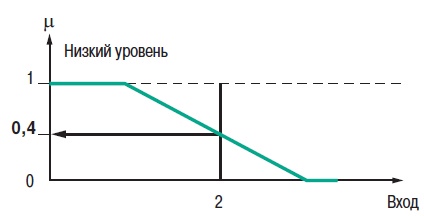



Рис. 7. Подготовка задачи - фаззификация

2.3. Операторы нечеткой логики

Операторы используются для записи комбинаций логических понятий нечеткой логикой, чтобы вычислять степени истинности. Применяются стандартные логические операторы AND, OR и NOT.

Пример: Подходящая квартира = Разумная цена аренды AND Достаточная площадь.

Выбор операторов

Существует несколько вариантов этих операторов (см. приложение). Чаще всего используются операторы Заде, описанные далее.

Степень истинности предположения А записывается как μ(A).

Пересечение

Логическим оператором пересечения множеств является оператор AND. Степенью истинности предположения “A AND B” является минимум из степеней истинности A и B:

μ(A AND B) = MIN(μ(A),μ(B))

Например:

“Низкая Температура” истинно на 0,7.

“Низкое Давление” истинно на 0,5.

Поэтому утверждение “Низкая Температура“ AND “Низкое Давление” истинно на 0,5 = MIN(0,7; 0,5).

ВАЖНО: при использовании AND в нечеткой логике результат аналогичен классической логике: 0 и 1 получается 0.

Объединение

Логическим оператором объединения множеств является оператор OR. Степенью истинности предположения “A OR B” является максимум из степеней истинности предположений A и B:

μ(A OR B) = MAX(μ(A),μ(B))

Например:

“Низкая Температура” истинно на 0,7.

“Низкое Давление” истинно на 0,5.

Поэтому утверждение “Низкая Температура“ OR “Низкое Давление” истинно на 0,7.

ВАЖНО: при использовании OR в нечеткой логике результат аналогичен классической логике: 0 OR 1 получается 1.

Отрицание

Логический оператор отрицания обозначается NOT.

μ(NOT A) = 1 - μ(A)

Например:

“Низкая Температура” истинно на 0,7.

Поэтому утверждение NOT “Низкая Температура” (можно записать как “Температура НЕ низкая”) истинно на 0,3.

ВАЖНО: при использовании NOT в нечеткой логике результат аналогичен классической логике NOT(0) получается 1 и NOT(1) получается 0.

Язык лестничных схем для нечеткой логики

Язык лестничных схем – это графический язык, который обычно используется инженерами систем управления для написания логических условий в классических описаниях алгоритмов. Компания Schneider предложила использовать этот же язык для описания выражений нечеткой логики.

Ниже приведен пример описания системы управления климатом:

горячий, влажный воздух не комфортен (формируется испарина); аналогично дыхание затруднено, если воздух холодный и очень сухой. Наиболее комфортная ситуация, когда воздух горячий и сухой или холодный и влажный. Эти формулы могут быть описаны на языке лестничных схем для нечеткой логики (рис. 8):

Комфорт = (Низкая температура AND Высокая влажность) OR (Высокая температура AND Низкая влажность).

Это логическое выражение описывает ощущение человека в помещении, в котором отсутствует принудительная циркуляция воздуха.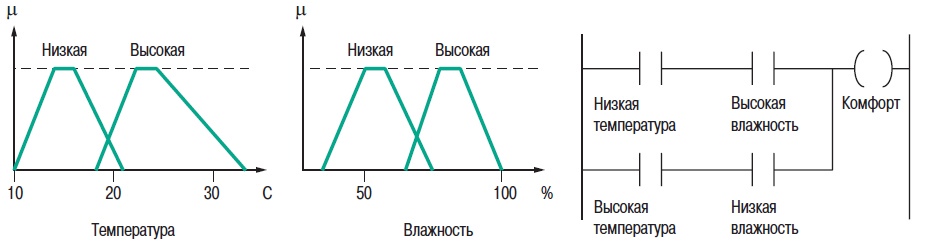



Рис. 8. Язык лестничных схем для нечеткой логики

Классификация нечеткой логики

Классификация обычно состоит из двух частей:

— подготовка: определение рассматриваемых классов;

— во время работы: назначение элементов классам.

Понятия классов и множеств идентичны с обычной логикой.

Существует три типа методов назначения в соответствии с получаемым результатом:

— двоичный: элемент либо принадлежит, либо не принадлежит классу;

— вероятностный: элемент, вероятно, принадлежит двоичному классу, например, установка диагноза по симптомам, которые перечисляет пациент (диагностирование),

— градационный: элемент имеет степень принадлежности какому-либо классу, например, «салат» принадлежит к группе «свежая зелень».

Методы классификации, независимо от типа выдаваемого результата: двоичный, вероятностный или градуированный, могут быть реализованы через:

— эксперимент (в случае применения языка лестничных схем для нечеткой логики, описанной выше);

— примеры, используемые для учебных целей (например, классификаторы нейронных сетей);

— математических или физических знаний о проблеме (например, комфортность тепловой обстановки может быть получена из уравнений теплового баланса).

Градационный (или нечеткий) метод классификации может использоваться для управления петлями регулирования. Примером этого может служить промышленная печь для производства бисквитов, описание которой приводится далее.

2.4. Правила в нечеткой логике

Нечеткая логика и искусственный интеллект

Целью базовых правил нечеткой логики является формализация и применение человеческого умозаключения. Таким образом, нечеткая логика является частью искусственного интеллекта. Базы правил нечеткой логики являются наиболее часто используемым инструментов в приложениях с нечеткой логикой. Базы правил нечеткой логики представляют собой набор правил, которые обычно используются параллельно, но в некоторых приложениях могут быть объединены.

Применяются правила следующего типа:

IF “утверждение” THEN “результат.

Например: IF “высокая температура“ AND “высокое давление” THEN “хорошая вентиляция“ AND “открытый клапан”.

Базы правил нечеткой логики, подобно традиционным экспертным системам, основываются на базе знаний, построенной на основе человеческого опыта. В то же время существует существенные отличия в обработке и характеристиках этих знаний (см. рис. 9).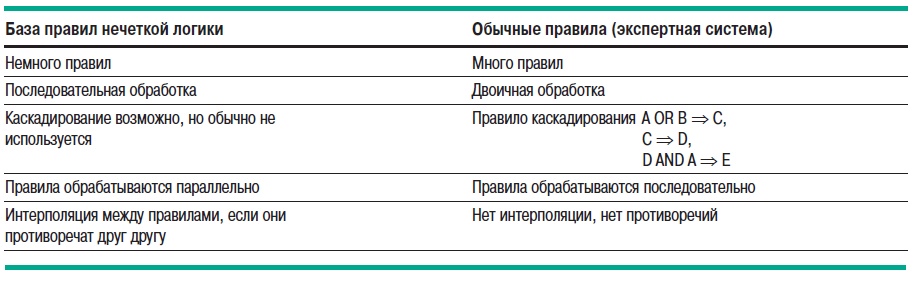



Рис. 9. Нечеткая логика и традиционная

Процесс обработки нечеткой логики состоит из трех частей (см. рис. 10).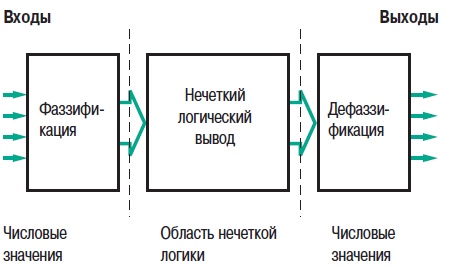



Рис. 10. Процесс обработки нечеткой логики

Утверждение

Утверждение (также известное, как преположение или условие) является комбинацией предположений и операторов AND, OR, NOT.

“Высокая температура” и “Высокое давление” предположения из примера выше, соединенные оператором AND, образуют правила.

Нечеткий логический вывод

Наиболее часто используется механизм нечеткого логического вывода, называемый механизмом Мамдани. Он представляет собой упрощение более общего механизма, который базируется на “нечетком выводе” и обобщенном правиле дедукции (generalised modus ponens). Информация о этих концепциях приведена в приложении. Далее используются только базы правил Мамдани.

Результат

Результат нечеткого правила представляет собой комбинацию предложений объединенных операторами AND. В примере, представленном выше “хорошая вентиляция” и “открытый клапан” являются предложениями этого правила.

Инструкция “OR” не используется при формировании предложений результата, потому что она вносит неоднозначность в правило (при этом для выявления корректной обработки необходима дополнительная экспертиза). Обработка неоднозначностей не рассматривается механизмом логического вывода Мамдани, он обрабатывает только неточности. Поэтому правила нечеткой логики, основанные на механизме Мамдани не подходят для применения в медицине, где результаты неоднозначны. Теория вероятностей, предложенная Лотфи Заде, описывает соответствующую методику для этих целей.

Отрицание таже не применяется предложений результата в механизме Мамдани. Поскольку, если правило имеет результат THEN “вентиляция HЕ в среднем положении” это не означает, что можно сказать “слабая вентиляция” или “сильная вентиляция”. Это представляет собой еще один вариант неопределенности.

Механизм логического вывода Мамдани

Основная идея:

База нечетких правил Мамдани содержит лингвистические правила, использующие функции принадлежности для описания применяемых концепций (см. рис. 11).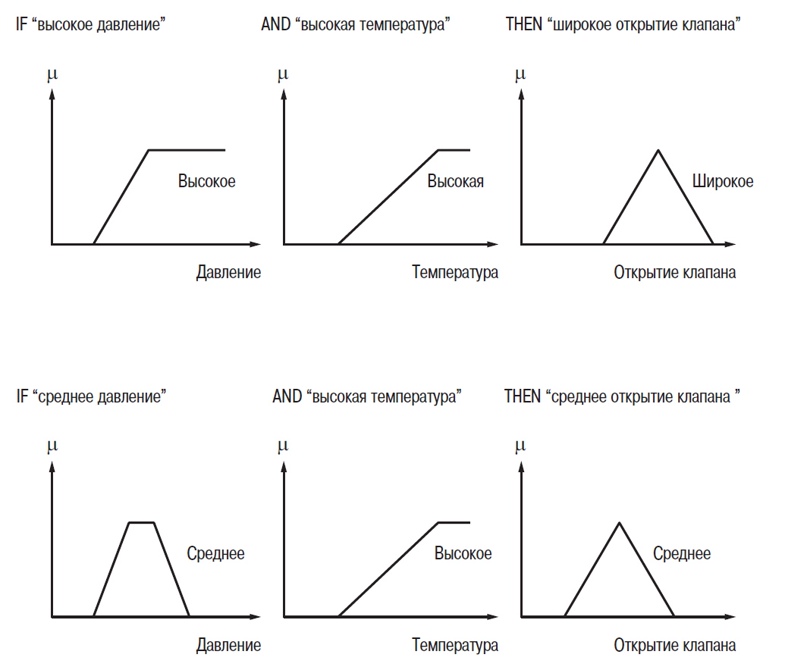



Рис. 11. Результат правила

Механизм логического вывода состоит из следующих этапов:

— Постановка задачи (фаззификация)

Процесс фаззификации заключается в выведении функций принадлежности, используемых в утверждениях правил как показано на рис. 12: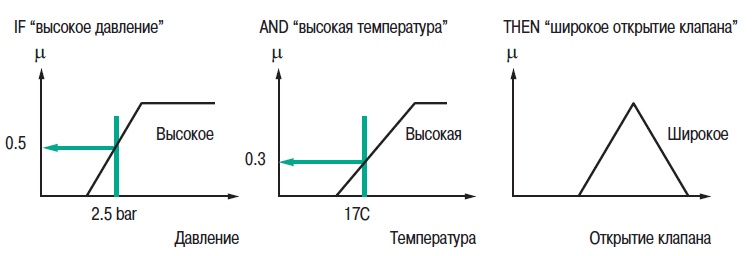



Рис. 12. Фаззификация

— Степень активизации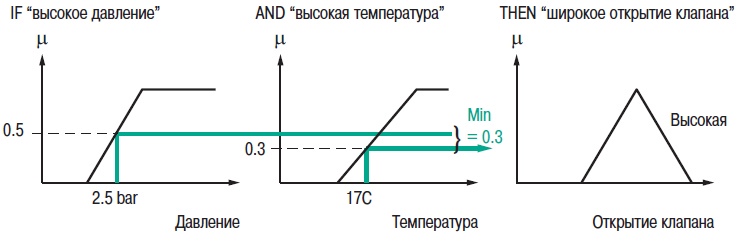



Рис. 13. Активизация

— Результат

Степень активизации правила используется для того, чтобы определить результат правила: данная операция называется выводом результата. Применяются несколько операторов вывода результата (см. приложение), чаще всего используется оператор выбора минимума.

Результирующее нечеткое множество строится с помощью поиска минимальных значений среди степеней активизации и функций принадлежности и сортировки «урезанных» функций принадлежности (см. рис. 14).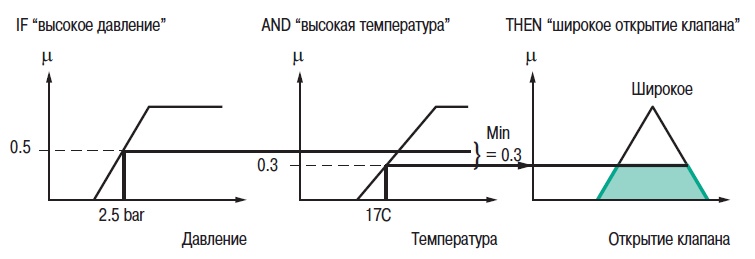



Рис. 14. Вывод результата

— Объединение

Общее выходное нечеткое множество получается путем объединения нечетких множеств, полученных в результате применения каждого правила формирования для данного выхода. На примере ниже представлен случай, когда на формирование одного выхода влияют два правила. Предполагается, что правила связаны логической операцией “OR”, поэтому необходимо найти максимальное значение среди результирующих функций принадлежности для каждого правила (см. рис. 15).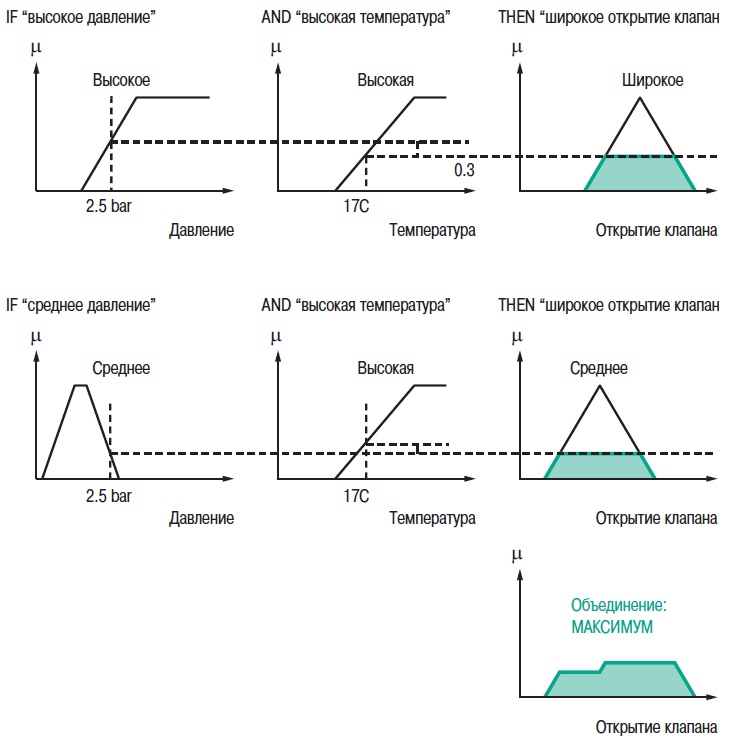



Рис. 15. Объединение правил

Дефаззификация

На последнем этапе нечеткого логического вывода, выходное нечеткое множество уже определено, но оно не может быть напрямую использовано для предоставления оператору точной информации или для управления исполнительным механизмом. Необходимо выполнить переход из “мира нечеткой логики” в “реальный мир”: этот этап называется дефаззификация.

Можно использовать разнообразные методы дефаззификации, однако чаще всего используется метод вычисления “центра тяжести” нечеткого множества (см. рис. 16).



Рис. 16. «Центр тяжести» нечеткого множества

“Свободные” правила и правила “возможности”

В базах нечетких правил, в общем случае, используются функции принадлежности для системных переменных и правила, которые могут быть записаны в текстовом виде. В каждом правиле используется свой вход и выход, как показано в примере ниже:

R1:

IF “Высокая температура”

THEN “Высокий выход”

R2:

IF “Средняя температура”

AND “Низкое давление”

THEN “Средний выход”

R3:

IF “Средняя температура”

AND “Высокое давление”

THEN “Низкий выход”

R4:

IF “Низкая Температура”

AND “Высокое давление”

THEN “Очень низкий выход”

“Зоны действия” правил и их наложения могут быть представлены в виде графической диаграммы, показанной на рис. 17.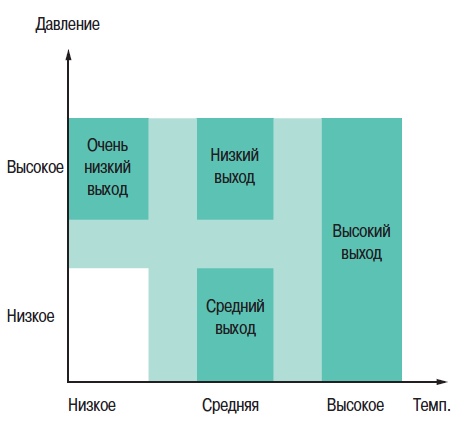



Рис. 17. Результаты применения правил

Можно сделать следующие наблюдения:

— нет необходимости покрывать все области: в данном случае комбинация «Низкая температура» и «Низкое давление» не рассматривается. Это можно объяснить, например, тем, что данная комбинация физически невозможна для данного механизма, или тем, что она не представляет интереса. Такая графическая диаграмма является лучшим способом проверки на наличие возможных ошибок или упущений;

— первое правило учитывает только параметр «Температура»: это нормально, потому что отражает существующий опыт.

Однако, для многих приложений определяют «таблицы» правил. При таком подходе, все пространство разбито на ячейки и каждой ячейке назначено правило. Преимуществом такого подхода является его методичность, однако:

— он не всегда позволяет использовать простое выражение существующего накопленного опыта (с минимальным количеством правил),

— он может применяться только для двух или трех входов, тогда как базы ”свободных” правил могут быть построены на основе большого количества переменных.

Замечания

— Поведение базы нечетких правил зависит от входов и является статичным и нелинейным.

— Базы нечетких правил сами по себе не являются динамическими, хотя они часто используют, как входы, переменные, отображающие динамику системы (производные, интегралы и т.д.) или время.

— Основным преимуществом контроллера с функцией нечеткого ПИД-регулирования, часто представляемого как учебный пример для объяснения идеи нечеткой логики, является выполнение нелинейного ПИД-регулирования, которое может быть использовано вместо традиционного ПИД-регулирования. Более того, при традиционном подходе трудно учесть весь накопленный опыт для конкретного применения.