Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил. Твердое тело

• Название: Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил. Твердое тело
• Дата: 20.06.2022
• Размер: 431.47 Kb.
• Имя файла: Tekh_Mekh.docx
• Тип: Документы; #606335
• страница: 3 из 5

Понятие о напряжении

Согласно гипотезе 1 (см. п. 2.1.1) можно предположить, что внутренние силы непрерывно распределены по площади поперечного сечения бруса. Пусть на малую, но конечную площадку А (рис. 2.5) действует внутренняя элементарная сила R. Разложив R на составляющие по осям   получим ее компоненты   Отношение вида

 (2.2)

определяет среднее напряжение на данной площадке в данной точке.

Полное, или истинное, напряжение в точке есть отношение

 (2.3)

которое определяет интенсивность внутренних сил в данной точке рассматриваемого сечения. Поскольку через точку тела можно провести бесчисленное множество сечений, то в данной точке имеется бесчисленное множество напряжений, связанных с площадками действия. Совокупность всех напряжений, действующих на разных площадках в данной точке, называется напряженным состоянием точки. Единица напряжения – Н/м2 или Па. По аналогии с выражением (2.3) можно записать:

 (2.4)

 (2.5)

 (2.6)

Выражение (2.4) определяет нормальное напряжение σx (рис. 2.6), вектор которого направлен так же, как и вектор нормальной силы Νx. Выражения (2.5) и (2.6) определяют касательные напряжения  ; их векторы имеют те же направления, что и, соответственно,  и . Первый индекс при τ указывает, какой оси параллельна нормаль к площадке действия рассматриваемого напряжения, второй индекс показывает, какой оси параллельно данное напряжение.

Зависимость между полным напряжением К и его составляющими выражается формулой

 (2.7)

Рассмотрим связь между напряжениями и внутренними силовыми факторами в поперечном сечении бруса.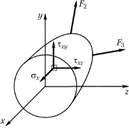



Рис. 2.5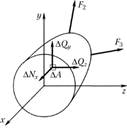



Рис. 2.6

Составляющие главного вектора и главного момента внутренних сил будут иметь следующий вид: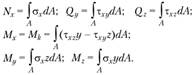

 (2.8)

23. Растяжение и сжатие, внутренние силовые факторы, напряжения, эпюры, деформации. Закон Гука.

Растяжение вызывает удлинение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба). В поперечных сечениях бруса возникает один внутренний силовой фактор — нормальная сила.

Сжатие — вид продольной деформации стержня или бруса, возникающей при приложении к нему нагрузки по его продольной оси. Сжатие — силовое воздействие на газообразное тело, приводящее к уменьшению занимаемого им объёма, а также к повышению давления и температуры.

Внутренние силовые факторы (ВСФ) в поперечном сечении бруса Проекции главного вектора R и главного момента M на ГЛАВНЫЕ ЦЕНТРАЛЬНЫЕ ОСИ поперечного сечения и ПРОДОЛЬНУЮ ось бруса называются ВНУТРЕННИМИ СИЛОВЫМИ ФАКТОРАМИ (ВСФ) в поперечном сечении.

Закон Гука формулируется так: сила упругости, которая возникает при деформации тела, вследствие приложения сторонних сил, пропорционально его удлинению. Деформация в свою очередь это изменение межатомных или межмолекулярных расстояние вещества под действием внешних сил

24. Диаграмма растяжения низко углеродистой стали. Механические свойства пластичных и хрупких материалов.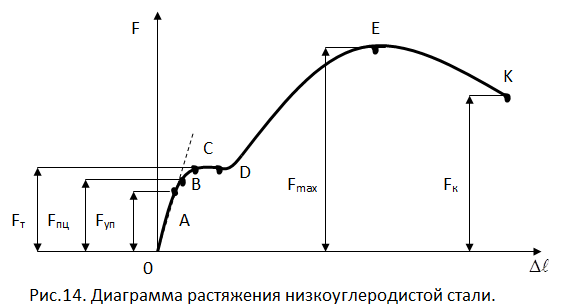


Способность материала получать большие остаточные деформации, не разрушаясь, назовём пластичностью. Материалы, обладающие такой способностью, именуют пластическими, к ним относятся сталь, бронза, алюминий и другие.

Способность материала разрушаться без образования заметных остаточных деформаций назовём хрупкостью. Материалы с такой способностью именуют хрупкими, к ним относятся чугун, камень, бетон, стекло и другие.

25. Коэффициент запаса прочности. Условия прочности. Три вида расчетов на прочность при растяжении и сжатии.

Коэффициент запаса — величина, показывающая способность конструкции выдерживать прилагаемые к ней нагрузки выше расчётных. Наличие запаса прочности обеспечивает дополнительную надёжность конструкции, чтобы избежать повреждений и разрушения в случае возможных ошибок проектирования, изготовления или эксплуатации.

Условия прочности позволяют оценивать прочность элементов конструкций при соответствующем нагружении, сравнивая максимальные напряжения, действующие в них с допустимыми значениями.

В сопротивлении материалов основным критерием надежности конструкции является ее прочность.

В зависимости от цели расчета (постановки задачи) различают три вида расчетов на прочность: 1) проверочный, 2) проектный и 3) определение допускаемой нагрузки.

26. Срез. Внутренние силовые факторы, напряжения, Условие прочности.

Срез - разрушение соединительных деталей под действием поперечных нагрузок (т.е. перпендикулярных осям этих деталей).

Например, разрушение штифта может произойти при штифтовом соединении двух деталей, которые нагружены двумя противоположно направленными силами. Вместо штифта может быть шпонка, болт, шпилька, заклепка.

Допущения при расчете на срез:
- в поперечном сечении детали, где может быть срез, возникает только поперечная сила Q
- касательные напряжения распределены по поперечному сечению равномерно
- при соединении несколькими одинаковыми деталями – все они нагружены одинаково

Условие прочности при расчете на срез:


- расчетное напряжение среза
Q = F/i – поперечная сила в сечении
i – число соединительных деталей (например, число заклепок)
Aср – площадь поперечного сечения срезаемой детали (заклепки)
 - допускаемое напряжение

Три вида расчетов на срез:
- проверочный
- проектировочный – определение числа соединительных деталей или размеров деталей
- определение допускаемой нагрузки

27 Смятие. Внутренние силовые факторы, напряжения, условие прочности.

Смятие – разрушение от давления между поверхностями соединительной детали и отверстия (при штифтовом, шпоночном соединениях и т.д.). При изменении формы отверстия от давления соединение разрушается.

Допущения при расчете на срез:
- силы давления распределены по поверхности смятия равномерно
- силы давления перпендикулярны поверхности смятия

Условие прочности при расчете на смятие:

F/i – нагрузка на один соединительный элемент
i – число соединительных элементов
Aсм – площадь смятия

 - допускаемое напряжение

28 Расчёты соединений заклёпками, штифтами.

Условия нагружения заклепок при заклепочном соединении двух листов металла и штифтов, соединяющих, например, обод зубчатого колеса с корпусом в планетарном редукторе, практически одинаковы. Схема штифтового соединения показана на рис. 6.4.



Рис. 6.4. Схема штифтового соединения

Расчет штифта на срез. Из условия прочности на срез ^среза- ч [^тсреза1* Штифт может срезаться по круглому поперечному сечению. Площадь среза Л_среза = л(/²/4. Приравнивая два выражения Л_среза, определяем диаметр штифта d.

Расчет на смятие. Из условия смятия находим допускаемую площадь смятия А_смкт > F/ [о_смят |. Реальная площадь смятия определяется толщиной скрепляемых штифтом деталей. Истинная поверхность смятия — это зона контакта листа металла и штифта на поверхности цилиндра, но размер ее и распределение напряжений на ней неизвестно. Напряжения на поверхности контакта распределяются по сложному степенному закону.

Удовлетворительные результаты расчета получаются, если взять в качестве площади смятия проекцию криволинейной поверхности цилиндра на диаметральную плоскость А_смят = d/z, где И — наименьшая из толщин соединяемых деталей. Если детали разной прочности, то возможно потребуется проверка прочности на смятие обеих деталей. Приравнивая два выражения Л_смят, находим допустимую толщину детали И.

Обычно толщина листов задана, тогда диаметр штифта или заклепки определяют дважды (из условий прочности на срез и на смятие). Окончательно принимают диаметр, удовлетворяющий обоим условиям прочности. Расчет заклепочного соединения абсолютно аналогичен расчету штифтового соединения.

29 Кручение. Внутренние силовые факторы, напряжения, эпюры.

КРУЧЕНИЕ

Внутренние силовые факторы при кручении. Построение эпюр крутящих моментов

Кручением называется такой вид нагружения, при котором в поперечных сечениях возникает внутренний силовой фактор — крутящий момент Л/, (рис. 6.1).



Рис. 6.1. Действие крутящего момента на одном участке

В дальнейшем стержень, работающий на кручение, будем называть валом.

Крутящие моменты в поперечных сечениях вала определяются с помощью метода сечений. Принципиально эпюры Л/, строят так же, как эпюры продольных сил. В сечении, где определяется крутящий момент, вал мысленно рассекают плоскостью, одну часть (любую) отбрасывают и, рассматривая равновесие оставленной части, вычисляют крутящий момент через внешние скручивающие (вращающие) моменты, приложенные к этой части вала.

Таким образом, крутящий момент, возникающий в произвольном сечении вала, численно равен алгебраической сумме внешних вращающих моментов, действующих на вал по одну сторону от рассматриваемого сечения. Найденные значения крутящих моментов в произвольно выбранном масштабе откладываются на графике с учетом знака крутящего момента.

Знак крутящего момента не имеет физического смысла, но для определенности при построении эпюр примем следующее правило: крутящий момент будем считать положительным, если наблюдатель, глядя на поперечное сечение со стороны внешней нормали, видит крутящий момент направленным против часовой стрелки. При построении эпюр удобнее устанавливать знак крутящего момента через действующие на вал внешние моменты. Положительный крутящий момент вызывается действием моментов, стремящихся повернуть отсеченную часть по часовой стрелке, если смотреть со стороны внешней нормали к проведенному сечению.

Рассмотрим примеры построения эпюр крутящих моментов.

Найдем крутящие моменты на участках вала, изображенного на рис. 6.2, а. Воспользуемся методом сечений и определим крутящий момент А/,] на участке I (рис. 6.2, б). На левую часть вала действует только один внешний момент, равный А/. Этот момент будет закручивать указанную часть вала против часовой стрелки, если смотреть со стороны внешней нормали к проведенному сечению. Тогда согласно принятому правилу знаков А/;1 = -А/.



Рис. 6.2. Действие крутящего момента на различных участках: а — расчетная схема; 6 — действие крутящего момента на первом участке; в — действие крутящего момента на втором участке; г — действие крутящего момента на третьем участке; д — эпюра крутящих моментов

На участке II найдем крутящий момент М,и через внешние моменты, действующие на ват левее проведенного сечения (рис. 6.2, в). Согласно принятому правилу знаков М,п = -М + 3М = 2М.

На участке III удобнее рассмотреть равновесие правой части стержня, на которую действует один внешний момент, равный 4М, отбросив левую (рис. 6.2, г). Согласно принятому правилу знаков М1Ш = 4М.

Построим по найденным значениям эпюру крутящих моментов (рис. 6.2, д). Для этого проведем базовую линию (линию нулевых значений Л/,) параллельно оси стержня и отложим перпендикулярно к ней найденные по участкам значения крутящих моментов в некотором произвольно выбранном масштабе. В пределах каждого участка нагружения Мг не изменяется, поэтому эпюра состоит из прямых, параллельных базовой линии. В точках приложения сосредоточенных внешних моментов на эпюре Л/, имеются «скачки», равные этим моментам. Опасными будут все сечения третьего участка.

Рассмотрим второй пример. Стержень нагружен по всей длине равномерно распределенными моментами интенсивностью М/1 (рис. 6.3, а). Проведем сечение на расстоянии I от свободного конца вала и рассмотрим равновесие левой отсеченной части (рис. 6.3, б). Сумма внешних моментов, действующих на левую часть, должна уравновешиваться крутящим моментом, возникающим в рассматриваемом сечении.



Рис. 6.3. Стержень нагружен равномерно распределенными моментами:

а — расчетная схема; б — отсеченная часть; в — эпюра крутящих моментов



Крутящий момент в данном случае изменяется по линейному закону, а поэтому эпюра представляет собой наклонную прямую

(рис. 6.3, в). На левом конце вала, где I = О, М. = 0. На правом I= / и Мг =(М/^1 = м.

Зачастую при решении задач задаются не внешние моменты, передаваемые валом, а передаваемая валом мощность. В этом случае внешние моменты легко найти по формуле



(6.1)

где Р — мощность, выраженная в ваттах; со — угловая скорость вращения вала, измеряемая в радианах в секунду; в этом случае вращающий момент получается в ньютон-метрах.

Если частота п вращения вала задана в оборотах в минуту, то угловую скорость можно найти по формуле



(6.2)

Пример 6.1 [25, 26]. Построить эпюру крутящих моментов для вала, изображенного на рис. 6.4, а. Вал имеет постоянную частоту вращения п = 248 мин-1. Передаваемые мощности соответственно равны: Р2 = = 15 Вт; />3 = 7,5 кВт; Р4= 10 кВт. Моментами трения в опорах пренебречь.



Рис. 6.4. Определение крутящих моментов, передаваемых валом: а — расчетная схема; б — эпюра крутящих моментов

Вычислим вращающие моменты, передаваемые каждым из шкивов, предварительно определив угловую скорость вала:

со = пп/^ = со = 248^ = 25 рад/с;



= 600 Нм;



= 300 Н м;



= 400 Н • м.

При равномерном вращении вала алгебраическая сумма вращающих моментов должна быть равна нулю, откуда

М{ = М2 + М$ + М4 = 600 + 300 + 400 = 1300 Н м.

Для определения крутящих моментов воспользуемся методом сечений. На участках I и V вала крутящий момент М, = 0. Если рассечь вал плоскостью на участке II и отбросить его правую часть, то можно увидеть, что на оставшуюся часть будет действовать единственный момент М2, стремящийся повернуть ее против часовой стрелки, если смотреть на вал со стороны сечения; следовательно, согласно принятому правилу знаков М1П — -М2 — -600 Н м. Мысленно рассекая вал плоскостью на участке III и оставляя левую часть, находим

М:Ш = -М2 + М, = -600 + 1300 = 700 Н • м.

На участке IV удобнее оставить правую часть. На нее действует только момент М4, вращающий эту часть по часовой стрелке, значит, М.|у — М4 — 400 Н • м.

Теперь можно построить эпюру крутящих моментов (рис. 6.4, б).
30. Условия прочности и жесткости при кручении, Три вида расчетов напрочность и жесткость.

1. Проверочный расчет: максимальный относительный угол закручивания должен быть меньше или равным допускаемому.

, где  - полярный момент инерции сечения,   - допускаемый угол закручивания, 

Мz – крутящий момент,  G –это модуль сдвига.

2. Проектный расчет

Из условия жесткости подбор сечения (определяем полярный момент инерции сечения):



Для круглого сечения:



или при переходе к градусной мере:



3. Определение допускаемого крутящего момента

Допускаемый крутящий момент из условия жесткости:



31 Изгиб. Внутренние силовые факторы, напряжения, эпюры.

Изгибом называется вид деформации, при котором искривляется продольная ось бруса. Прямые брусья, работающие на изгиб, называются балками. Прямым изгибом называется изгиб, при котором внешние силы, действующие на балку, лежат в одной плоскости (силовой плоскости), проходящей через продольную ось балки и главную центральную ось инерции поперечного сечения.

Изгиб называется чистым, если в любом поперечном сечении балки возникает только один изгибающий момент.

При плоском поперечном изгибе в сечениях балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М. Для их определения используют метод сечений (см. лекцию 1). Поперечная сила Q в сечении балки равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.

Особенности эпюр внутренних силовых факторов при изгибе.

1. На участке балки, где нет распределенной нагрузки, эпюра Q представлена прямой линией, параллельной базе эпюре, а эпюра М — наклонной прямой (рис. а).

2. В сечении, где приложена сосредоточенная сила, на эпюре Q должен быть скачок, равный значению этой силы, а на эпюре М -точка перелома (рис. а).

3. В сечении, где приложен сосредоточенный момент, значение Q не изменяется, а эпюра М имеет скачок, равный значению этого момента, (рис. 26, б).

4. На участке балки с распределенной нагрузкой интенсивности q эпюра Q изменяется по линейному закону, а эпюра М — по параболическому, причем выпуклость параболы направлена навстречу направлению распределенной нагрузки (рис. в, г).

5. Если в пределах характерного участка эпюра Q пересекает базу эпюры, то в сечении, где Q = 0, изгибающий момент имеет экстремальное значение Mmax или Mmin 
32 Условия прочности при изгибе. Расчеты на прочность. Рациональные формы сечения балок.

Условие прочности в сопротивлении материалов имеет вид атах < [о]. Запишем выражение для отах: 

где W. = Jz/утах — момент сопротивления при изгибе.

Расчеты на прочность при изгибе.

1. При проверочном расчете определяется максимальное расчетное напряжение, которое сравнивается с допускаемым напряжением:



2. При проектном расчете подбор сечения бруса производится из условия:



3. При определении допускаемой нагрузки допускаемый изгибающий момент определяется из условия:



Далее по полученному значению [Mx] определяют допускаемые значения внешних поперечных нагрузок [Q] и внешних изгибающих моментов [Mвнеш]. Условие прочности имеет вид:



33 Линейные и угловые перемещения при изгибе. Расчёты на жёсткость. Касательные напряжения.

При прямом изгибе различают два вида перемещений: линейные перемещения, которые называются прогибы и угловые перемещения, которые называются углы поворота. Линейные перемещения (прогибы) измеряются расстоянием между центрами тяжести одного и того же поперечного сечения до и после деформации. Угловые перемещения (углы поворота) измеряются углами между осью бруса до деформации и касательной, проведённой к изогнутой оси бруса в каждой её точке.

Жесткость при изгибе вычисляют по формуле: Dи = Eи∙I, (4.1) где Eи – модуль упругости при изгибе, Па; I = bh3/12 – момент инерции поперечного сечения образца, М4 (b – ширина образца, м; h – толщина образца, м). При определении свойств материалов при изгибе применяют различные методы испытания: метод кольца; метод консоли; метод опоры пробы на двух опорах; метод продольного изгиба; определяют драпируемость и несминаемость материалов.

Максимальные нормальные напряжения при изгибе возникают в сечениях, где действует максимальный изгибающий момент, в точках сечения наиболее удаленных от нейтральной оси. Максимальные касательные напряжения возникают в сечениях балки, где действует максимальная поперечная сила. Касательные напряжения τmax обычно малы по сравнению с σmax и в расчетах, как правило, не учитываются.
34 Гипотезы прочности. Изгиб с кручением. Условия прочности. Расчеты на прочность при изгибе с кручением

Гипотезы прочности – это научные предположения об основной причине достижения материалом предельного напряженного состояния при сочетании основных деформаций.

Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары противоположных по направлению сил в его поперечной плоскости, точки приложения которых находятся на определённом удалении друг от друга. При этом данные силы образуют в поперечных сечениях тела единственный внутренний силовой фактор — крутящий момент. Примеры кручения: пружины растяжения-сжатия, валы.
Расчет прочности при изгибе с кручением производится по энергетической гипотезе прочности. В опасных точках при изгибе с кручением существует плоское напряженное состояние.



35 Детали машин. Основные понятия: машина, механизм, деталь. Требования к машинам и их деталям. Роль стандартизации в машиностроении.

Система деталей для передачи (преобразования движения одних звеньев в заданные другие) называется механизмом.

Машиной называется механизм, предназначенный для преобразования энергии материалов и информации с целью замены или облегчения физического и умственного труда человека.

Важным требованием к машинам является их социальная приспособленность, т.е. возможность обеспечивать безопасные и благоприятные условия труда обслуживающего персонала. Сюда относятся необходимая устойчивость против опрокидывания под воздействием внешних нагрузок, безопасность, утомляемость обслуживающего персонала при длительной непрерывной работе. Вредное влияние шума и вибрации на человека должно быть ограничено.

К деталям машин предъявляются следующие основные требования: технологичность - изготовление изделия при минимальных затратах труда, времени и средств при полном соответствии своему назначению; прочность - свойство детали в определенных условиях и пределах, не разрушаясь, воспринимать приложенные к ней нагрузки.

Стандартизация обеспечивает государственный контроль за соблюдением этих норм и требований.

36 Переменные напряжения. Циклы напряжений и их характеристики. Предел выносливости.

Переменному напряжению соответствует термин «Alternating Voltage», который можно дословно перевести как «чередующееся» или «перемежающееся» напряжение – напряжение, полярность которого постоянно изменяется. Аналог «постоянного» напряжения – «Direct Voltage» – можно перевести как «направленное» напряжение – напряжение, которое не меняет своей полярности.

Совокупность всех значений напряжений в течении одного периода называется циклом напряжений. Характеристиками циклов напряжений являются: максимальное напряжение цикла – σ max; минимальное напряжение цикла – σ min; среднее напряжение цикла– σ m = (σ max + σ min)/2; амплитуда цикла– σ a = (σ max – σ min)/2; Коэффициент асимметрии цикла– r= σ min / σ max. Циклы, имеющие одинаковые коэффициенты асимметрии цикла, называются подобными.

Преде́л выно́сливости (также преде́л уста́лости) — в науках о прочности: одна из прочностных характеристик материала, характеризующих его выносливость, то есть способность воспринимать нагрузки, вызывающие цикличные напряжения в материале.

Предел выносливости определяется, как наибольшее (предельное) максимальное напряжение цикла, при котором не происходит усталостного разрушения образца после произвольно большого числа циклических нагружений.

37.Сварные и клеевые соединения их расчёт при осевом нагружении.

Основным критерием работоспособности сварных швов является прочность. Расчет на прочность основан на допущении, что напряжения в шве распределяются равномерно как по длине, так и по сечению.

Соединения встык. Расчет стыковых швов (рис. 2.7) производят на растяжение или сжатие по сечению соединяемых деталей без учета утолщения шва. Условие прочности шва на растяжение

 (2.1)

где Q - осевая растягивающая нагрузка;

s – толщина шва (принимается равной толщине детали);

lш – дина шва;

и  - расчетное и допускаемое напряжения на растяжение для шва (см. табл. 2.1).



Рис. 2.7 Соединение встык

Соединения внахлестку угловыми швами. Расчет угловых швов производят на срез по опасному сечению I—I (см. рис. 2.4, а), совпадающему с биссектрисой прямого угла.

Расчетная высота опасного сечения шва равна k·sin 45°≈0,7k. Условие прочности шва на срез



 

где  и  - расчетное и допускаемое напряжения среза для шва (табл. 2.1);

lш - длина шва.

В соединении лобовыми швами lш=2lл (см. рис. 2.5, а), фланговыми швами lш=2lфд (см. рис. 2.5,6). В комбинированном сварном соединении (см. рис. 2.5, в) lш равна сумме длин всех лобовых и фланговых швов.
Клеевое соединение представляет собой систему, прочность которой определяется силой сцепления клея по склеиваемым материалам (адгезионные связи), а также силой сцепления частиц клея или частиц материала между собой (когезионные связи) 

При нагружении разрываются слабейшие связи. В зависимости от их вида различают адгезионное и когезионное (по клею и по материалу) разрушение.

Таким образом, формула для расчета клеевого соединения примет следующий вид:



где S - площадь склеиваемых поверхностей, см2;

Q - нормативная нагрузка, кг;

г= 1,1 коэффициент перегрузки;

ш = 0,6 -г- 0,8 - коэффициент условий работы;

п = 1,5 - коэффициент концентрации напряжений;

R - расчетное сопротивление, МПа.
38. резьбовые соединения классификация резьб

Резьбовое соединение — соединение деталей при помощи резьбы. Все знают, что такое резьба, все ее видели. Многим так же известно, что резьбы отличаются между собой, так как они имеют разные размеры, шаг и так далее. Однако не многие представляют, чем это регламентировано, а также что существует не только привычная для нас метрическая резьба цилиндрической формы, но и многие другие ее виды.

Резьбы классифицируются по следующим признакам:

− по форме поверхности, на которой нарезается резьба 

− цилиндрические и конические;

− расположению резьбы на поверхности стержня или отверстия

− внешние и внутренние; − форме профиля

− треугольные, прямоугольные, трапецеидальные, круглые;

− эксплуатационному назначению

− крепежные (метрические, дюймовые), крепежно-уплотнительные (трубные, конические) и ходовые (трапецеидальная, упорная, прямоугольная).

Резьбой называется поверхность, образованная при винтовом движении плоского контура по цилиндрической или конической поверхности, другими словами, спираль с постоянным шагом, образованная на этой поверхности.

В зависимости от формы поверхности различают цилиндрические и конические резьбы. Оба этих типа резьб могут быть наружными и внутренними. По направлению витков нарезка может быть левой или правой. Ключевым параметром для классификации является тип профиля нарезки. По этому признаку выделяют следующие виды резьбовых соединений деталей: метрическая; дюймовая; трубная цилиндрическая; трапецеидальная; упорная; круглая.
39. расчет резьбовых соединений

Поэтому расчет на прочность резьбового соединения проводят только по одному основному критерию - прочности резьбовой части стержня при растяжении: – осевая сила, растягивающая болт, Н; – допускаемое напряжение при растяжении, МПа; расчетная площадь поперечного сечения нарезанной части болта, мм 2.

40. Шпоночные соединения .соединения призматическими шпонками.

Соединение охватывающей и охватываемой детали для передачи крутящего момента с помощью шпонки. Шпоночное соединение позволяет обеспечить подвижное соединение вдоль продольной оси. Классификация соединений в зависимости от формы шпонки: соединения призматическими шпонками, соединения клиновыми шпонками, соединения тангенциальными шпонками, соединения сегментными шпонками, соединения цилиндрическими шпонками.

Шпоночные соединения –это разборные подвижные или неподвижные соединения двух деталей, с применением специальных закладных деталей – шпонок. Шпонка – это деталь, устанавливаемая в пазах двух соединяемых деталей.

Наиболее распространены призматические шпонки, устанавливаемые в пазу вала по посадкам с натягом Р9/h9 (врезные шпонки) или по посадке Js9/h9 (закладные шпонки). Шпонки входят в паз ступицы так, что между верхней гранью шпонки и днищем паза оставляют зазор s

Достоинства шпоночного соединения – простота конструкции и сравнительная легкость монтажа и демонтажа, благодаря чему шпоночные соединения применяют во всех отраслях машиностроения.

Недостаток – шпоночные пазы ослабляют вал и ступицу насаживаемой на вал детали. Ослабление вала обусловлено не только уменьшением его сечения, но главное, значительной концентрацией напряжений изгиба и кручения, вызываемой шпоночным пазом. Шпоночное соединение трудоемко в изготовлении.

41. Сегментные шпонки

Сегментные шпонки, или шпонки Вудруфа (табл. 10), обладают некоторыми технологическими преимуществами по сравнению с призматическими шпонками. Пазы на валах обрабатываются дисковыми фрезами с большей производительностью и точностью, чем для призматических шпонок. Шпонки изготовляют из чистотянутых сегментных профилей, а в мелкосерийном производстве — из цилиндрического проката с разрезанием на сегменты. Демонтаж шпонок несложен и осуществляется легким ударом по концу шпонки.

Крепление шпонок на валу устойчивее вследствие большей глубины врезания. Однако сегментные шпонки значительно ослабляют валы (особенно полые). Это обстоятельство наряду с малой длиной шпонок, обусловливающей повышенные напряжения смятия на рабочих гранях шпонок, ограничивает применение сегментных шпонок областью малонагруженных соединений. Сегментные шпонки, за редким исключением, устанавливают только в массивных валах.

1. 
   Передачи их классификации. Механические передачи. Основные кинематические и силовые соотношения.
   

Передача – механизм, служащий для передачи движения от двигателя к исполнительному органу, как правило, с преобразованием скорости и изменением вращающегося момента.

Основные функции механических передач:

1.изменение скорости

2.изменение направления движения

3.преобразования вида движения: вращательного в поступательное и наоборот, равномерное в прерывистое

4.приведение в движение одним двигателем нескольких механизмов

Во всех механических передачах различают два основных звена: входное (ведущее) и выходное (ведомое). Между этими звеньями в многоступенчатых передачах располагаются промежуточные звенья. Звенья, передающие вращающий момент, называют ведущими, а звенья, приводимые в движение от ведущих, – ведомыми.

Параметры передачи, относящиеся к ведущим звеньям, будем отмечать индексом 1, а к ведомым - индексом 2, т. е. d1, v1 , ω1, P1, M1 – соответственно диаметр, окружи ная скорость, угловая скорость, мощность, вращающий момент на ведущем валу; d2, v2, ω 2, P2, M2 – то же, на ведомом.



Рис. 3.1

Любая механическая пе-редача характеризуется следующими основными параметрами (рис. 3.1): мощностью Р2 – на выходе, кВт; быстроходностью, которая выражается угловой скоростью ведомого вала ω2, рад/с, или частотой вращения n, измеряемой в об/мин (мин-1), и передаточным отношением u.

Это три основные характеристики, необходимые для проектировочного расчета любой передачи.

Кроме основных различают производные характеристики, которыми часто пользуются при расчетах.

Коэффициент полезного действия (КПД)

η = Р2 / Р1

Для многоступенчатой передачи, состоящей из нескольких отдельных последовательно соединенных передач, общий КПД определяют по формуле

ηобщ = η1η2η3…ηn                                                                                (4.1)

где η1, η2– ηn – КПД каждой кинематической пары, а также других звеньев привода, где имеются потери мощности (подшипники, муфты).

Окружная скорость ведущего или ведомого звена (м/с)

v = ωd/2,

где d – диаметр катка, шкива, колеса и др., м.

Окружная сила передачи (Н)

Ft = P / v = 2M / d,

где Р – в Вт.

Вращающий момент (Н*м)

М = P / ω = Ftd/2,

где Р – в Вт; d – в м; ω – в рад/с.

Вращающий момент ведущего вала M1 является моментом движущих сил; его направление совпадает с направлением вращения вала. Момент ведомого вала М2 – момент сил сопротивления, поэтому его направление противоположно направлению вращения вала.

Передаточным отношением механической передачи на-зывается отношение угловой скорости ведущего звена к угловой скорости ведомого звена. Передаточное отношение, определяемое в направлении потока мощности от ведущего звена к ведомому, обозначим u12; тогда расчетная формула имеет вид u12 = ω1 / ω 2 = n1 / n2,

где ω – в рад/с; n – в мин-1.

Если передача многоступенчатая (см. рис. 2.4), то ее

передаточное отношение равно произведению передаточных отношений ступеней, т. е.

uобщ = u1u2...un.                                                           (4.2)

При выполнении кинематических расчетов может возникнуть необходимость в определении угловой скорости ведомого вала при известном диаметре и окружной скорости колеса шкива, звездочки и т. п.; тогда

ω = 2v / d,                                                                      (4.3)

где v – в м/с; d – в м.

Если заданы шаг цепи t (мм) и число зубьев звездочки z, то определяют диаметр делительной окружности звездочки

dд = t /sin(180°/z)                                                         (4.4)

и далее угловую скорость ведомого вала–по формуле (4.3) » Учитывая,   что   в   большинстве  случаев   v1 = v2   или

ω1d2 = ω2d2/2, имеем ω1/ω2 = d2/d1 = и.

При необходимости передаточное отношение можно определить по вращающим моментам на ведущем и ведомом валах

M1 = P1 / ω1 и M2 = P2 / ω2

или M2/M1 = P2ω1/(P1ω2).

Следовательно, u12 = M2 / (ηM1).

Итак, передаточное отношение для рассматриваемого примера будет иметь вид

u12 = ω1/ω2 = d2/d1 = М2 / (М1η).

При u12 > 1, ω1 > ω2 – передача понижающая; ее называют редуктором.

При u12 < 1, ω1 < ω2 – передача повышающая; ее называют мультипликатором.

8 Брак по семейному праву - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Передаточным числом называют отношение числа зубьев большего колеса к числу зубьев меньшего колеса и обозначают той же буквой u, но без индексов:

где z2 – число зубьев колеса (большего); z1 – число зубьев шестерни (меньшего колеса).

Передаточное число в отличие от передаточного отношения всегда положительное и не может быть меньше единицы. Передаточное число характеризует передачу только количественно. Передаточное число и передаточное отношение могут совпадать только у передачи внутреннего зацепления. У передач внешнего зацепления они не совпадают, так как имеют разные знаки: передаточное отношение – отрицательное, а передаточное число – положительное.

Наиболее распространены понижающие передачи, так как частота вращения исполнительного механизма в большинстве случаев меньше частоты вращения вала двигателя.

Если ведущее и ведомое колеса вращаются в одну сторону (например, у зубчатой передачи с внутренним зацеплением, см. рис. 3.4, г), то передаточное отношение считается положительным. Если ведомое и ведущее колеса вращаются в разные стороны (например, у зубчатой передачи внешнего зацепления, см. рис. 3.4, д), то передаточное отношение считается отрицательным.

Передачи выполняют с постоянным или переменным (регулируемым) передаточным отношением. Как те, так и другие, широко распространены. Регулирование передаточного отношения может быть ступенчатым или бесступенчатым. Ступенчатое регулирование реализуется в коробках передач с зубчатыми колесами, в ременных передачах со ступенчатыми шкивами и т. п.; бесступенчатое регулирование – с помощью фрикционных, ременных или цепных вариаторов. Заметим, что ступенчатое регулирование дешевле и осуществляется более простыми и надежными механизмами. Механизмы бесступенчатого регулирования позволяют менять угловую скорость на ходу и выбирать оптимальные законы движения. Применение того или иного способа регулирования передаточного отношения зависит от конкретных условий работы машины, которую обслуживает передача. Вообще передаточное отношение следует считать основной кинематической характеристикой передач.

2. 
   Фрикционные передачи. Условие работоспособности достоинства и недостатки ,классификация, расчёт.
   

Фрикционная передача – передаточный механизм, располагающийся в приводах машин. Она используется для трансформации механической энергии по частоте вращения и передаваемым усилиям. Они позволяют осуществлять бесступенчатое регулирование скорости и отличаются высоким КПД. Фрикционные механизмы изучаются технической механикой и используются в промышленности.

Фрикционные передачи состоят из 2 тел вращения: ведомого и ведущего катков, насаженных на валы. Передача вращательного движения производится посредством силы трения, появляющейся на площадках контакта рабочих тел под действием сил прижатия. Прижатие катков производится следующими способами:

1. 
   Посредством гидроцилиндров. Используется во время больших нагрузок.
   
2. 
   Собственным весом машины или ее узла.
   
3. 
   При помощи комплексных рычажных механизмов.