курсовая теория вероятности АГЗ МЧС. курсач. Статистическая обработка результатов выборки
 Скачать 170.24 Kb. Скачать 170.24 Kb.
|
|
Министерство Российской Федерации по делам гражданской обороны, чрезвычайным ситуациям и ликвидации последствий стихийных бедствий АКАДЕМИЯ ГРАЖДАНСКОЙ ЗАЩИТЫ Кафедра №72 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ ПО ВЫСШЕЙ МАТЕМАТИКЕ НА ТЕМУ «СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ВЫБОРКИ» Руководитель: Уфимцева А.М. Исполнитель: Макаров В.Ю. «305» учебная группа I. Целевая установка: Провести статистическое исследование случайной величины. II. Основные вопросы: 1) Графическое представление выборки; 2) Точечные оценки параметров распределения; 3) Интервальная оценка параметров распределения; 4) Статистическая проверка статистических гипотез. III. Исходные данные (обстановка): Выборка объёмом из 100 чисел и 20 чисел, надёжность, уровень значимости. IV. Перечень материалов, представляемых к защите: Пояснительная записка, включающая в себя теоретическую и практическую части. V. Перечень экспериментальных работ и расчетов на ЭВМ, проводимых в процессе работы над темой: Вычисление точечных оценок параметров, нахождение интервальных оценок, проверка различных статистических гипотез с помощью программы «Excel». VI. Общий объем и требования к оформлению отчетных материалов: 25 листов. VII. Перечень литературы: Гмурман В.Е. «Теория вероятностей и математическая статистика», Гмурман В.Е. «Руководство к решению задач по теории вероятностей и математической статистике», Фролов В.Д. «Учебно-методическое пособие по курсовой работе для студентов и курсантов вторых курсов (высшая математика)». VIII. Сроки представления выполненной работы руководителю и готовность ее к защите:________________________________ Руководитель: Уфимцева Александра Михайловна «_____» _______________ 2022 г. Задание получил: Макаров Вадим Юрьевич «» 2022 г. АннотацияВ данной курсовой работе, на основании данных выборки была выполнена проверка статистических гипотез. Для решения поставленной задачи использовались методы математической статистики: графическое представление выборки, вычисление точечных и интервальных оценок, критерия согласия Пирсона, критерий Стъюдента и хи квадрат ( 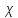 2). 2).Условие: в представленной таблице, показано количество граждан, подверженных угрозе наводнения из 100 населенных пунктов. Имея данные из 100 населенных пунктов построить вариационный ряд и статистическое распределение, эмпирическую функцию распределения, полигон частот, полигон относительных частот, гистограмму частот, гистограмму относительных частот, выборочное среднее, выборочную дисперсию и выборочное среднее квадратическое отклонение, доверительный интервал. Проверили гипотезу о нормальном распределении генеральной совокупности. СодержаниеАннотация 3 Введение 4 Теоретическая часть 5 Выборка и способы ее задания 5 Графические элементы анализа 6 Точечные оценки параметров распределения выборки 7 Интервальные оценки параметров распределения выборки 8 Статистическая проверка статистических гипотез 9 Часть I. Графическое представление выборки. 10 Часть 2. Точечные оценки параметров выборки 15 Часть 3. Проверка статистических гипотез. 16 Часть 4. Интервальные оценки параметров нормального распределения случайной величины 20 Заключение 22 Список использованной литературы: 23 ВведениеМатематическая статистика – наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющая оценивать надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании). Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов. Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования. В данной работе рассмотрены принципы статистических расчетов для выборки значения. Выборка состоит из 100 чисел. Для облегчения восприятия материала, значение выборки будем считать, как статистические данные по численности населения, в населенных пунктах, чаще подверженных наводнениям и затоплениям. Теоретическая частьВыборка и способы ее заданияГенеральной совокупностью называют полную совокупность объектов, из которых производится выборка. Выборкой называют совокупность случайно отобранных объектов из генеральной совокупности. Объемом выборки называют число объектов этой выборки. Если результаты выборки представлены числовыми значениями, то размах выборки — это разность между самым большим и самым малым значениями выборки. Наблюдаемые значения xi выборки называют вариантами, а их последовательность, записанная в возрастающем порядке, - вариационным рядом. Числа ni называют частотами соответствующих вариантов, wi = ni/n – относительными частотами. Статистическим распределением выборки называют перечень вариант и соответствующих им частот. Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения аргумента x относительную частоту наступления события, состоящего в том, что значение X выборочной варианты будет меньше x: 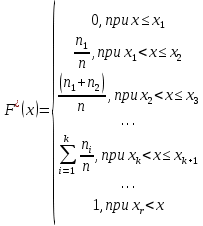 (1) (1)Графические элементы анализаГрафиком эмпирической функции распределения называют график функции F*(x). График строится на двух осях: на оси OX откладываются значения вариант xi, а на оси OY – значения функции F*(x). График представляет ступенчатую линию , начинающуюся с 0 для x ≤ x1, и монотонно поднимающуюся до значения 1 при xr Полигоном частот называют ломаную, отрезки которой соединяют точки (x1;n1), (x2;n2), …, (xr;nr). Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1,w1), (x2,w2), … , (xr,wr). Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы ∆iдлиной h и высотой ni/h (плотность частот). Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы ∆i длиной h и высотой wi/h (плотность относительных частот). Точечные оценки параметров распределения выборкиТочечной называют оценку, которая определяется одним числом. Точечные оценки обычно используют в тех случаях, когда число наблюдений велико. Выборочной средней xв называют среднее арифметическое значение вариант выборки. Если значения вариант x1, x2, …, xr имеют соответственно частоты n1, n2, …, nr, то 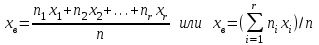 . (2) . (2)Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонений вариант xi от их среднего значения xв, т.е. 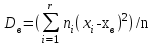 .(3) .(3)Выборочным средним квадратическим отклонением σв называют квадратный корень из выборочной дисперсии Dв 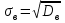 .(4) .(4)Исправленную (несмещенную оценку) дисперсию s2 выборки получают по формуле 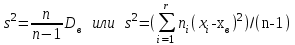 .(5) .(5)Аналогично вводится исправленное среднее квадратическое отклонение s 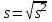 .(6) .(6)Интервальные оценки параметров распределения выборкиИнтервальной называют оценку, которая задается в виде интервала. Интервальные оценки удобно использовать в тех случаях, когда число наблюдений n относительно невелико. Надежностью оценки неизвестного параметра θ по вычисленному статистическими методами значению θ* называют вероятность γ, с которой выполняется неравенство | θ - θ*| < δ, при этом δ называется точностью оценки. В статистике обычно задаются надежностью γ и определяют точность δ. Доверительным интервалом для параметра θ называют интервал (θ* - δ, θ* + δ), который покрывает неизвестный параметр θ с вероятностью γ: P[θ* - δ Доверительный интервал с уровнем надежности γ для математического ожидания aпризнака X, распределенного нормально, при неизвестном среднем квадратическом отклонении определяется как 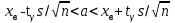 . (8) . (8)Доверительный интервал с уровнем надежности γ для среднего квадратического отклонения σ признака X, распределенного нормально, определяется как 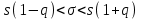 . (9) . (9)Статистическая проверка статистических гипотезСтатистической называют гипотезу (предположение) о виде неизвестного распределения или о параметрах известного распределения. Основной или нулевой гипотезой H0 называют выдвинутую гипотезу о неизвестном распределении, вместе с основной H0 выдвигается и конкурирующая (альтернативная) гипотеза H1, противоречащая основной. Основной принцип проверки статистических гипотез состоит в следующем: в зависимости от вида гипотезы и характера неизвестного распределения вводится функция K, называемая критерием, по значениям ее будет приниматься решение о принятии или отклонении основной гипотезы H0. Вводится также уровень значимости α как вероятность того, что будет отвергнута верная нулевая гипотеза и принята неверная гипотеза H1. Областью принятия гипотезы H0 называют те значения критерия K, при которых основная гипотеза H0 принимается, критической областью – отвергается. Для каждой выборки и конкретного вида критерия K по специальным таблицам находятся значения kкр, называемые критическими точками; критические точки отделяют область принятия гипотезы от критической области. Правосторонней называют критическую область, где K>kкр, левосторонней K Для проверки гипотезы о нормальном распределении генеральной совокупности c уровнем значимости α используется критерий χ2 Пирсона: 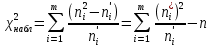 . (10) . (10)где 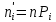 ; n – объем выборки, ; n – объем выборки, 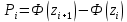 если значение критерия χ2набл меньше χ2кр, нет оснований отвергнуть основную гипотезу, если больше – основная гипотеза не принимается. Часть I. Графическое представление выборки.Исходные данные (41-140) : Таблица 1  1.Размах выборки R и объем выборки n. Используя функции Excel МИН или МАКС, задаем диапазон выбора, выделив всю рабочую часть таблицы. Находим xmin=137,3 и xmax=225,7. Размах выборки: R=xmax - xmin. R=225,7-137,3=88,4 Объем выборки по условию задачи n=100. 2.Разбиваем значения выборки на 10 интервалов. Для упрощения расчётов полагая их длины одинаковыми и равными ∆ = R/8= 88,4/10= 8,84 Таблица 2
3. Строим вариационный ряд выборки. Результаты выборки следует упорядочить (отсортировать) по возрастанию.. Для удобства расчетов в первом столбце приведены интервалы ∆i и их границы. Далее находим количество ni (частоты) вариант, попавших на интервалы ∆i и среднее значение xi ср случайной величины на соответствующем интервале. Таблица 3
По найденным значениям ni и xi ср составляем табл. 4, где проводим подсчеты для относительных частот wi = ni/n, приведенных частот Ni = ni/∆ и приведенных относительных частот Wi = wi/∆, отвечающих соответствующим интервалам ∆i. Проводим подсчеты для эмпирической функции распределения вероятностей: 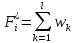 . .
4. Строим график эмпирической функции распределения вероятностей F*(x) 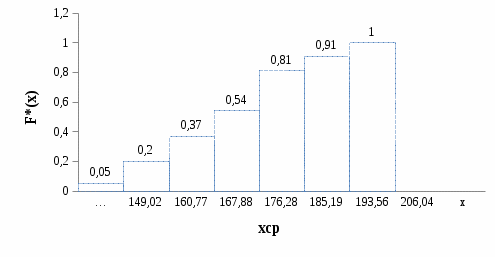 5. Строим полигон частот n(x). 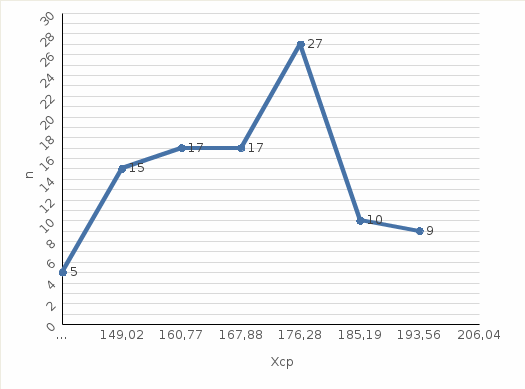 6. Строим полигон относительных частот w(x). 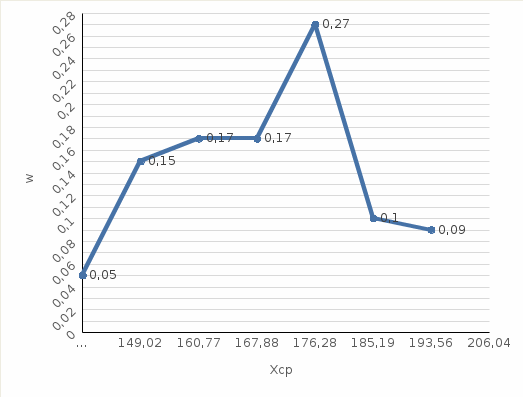 7. Строим гистограмму приведённых частот Ni(х). 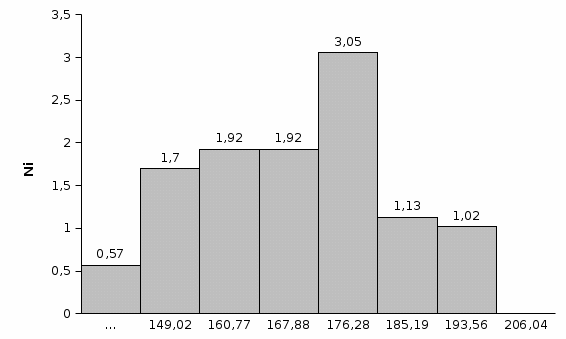 8. Строим гистограмму относительных частот Wi(х). 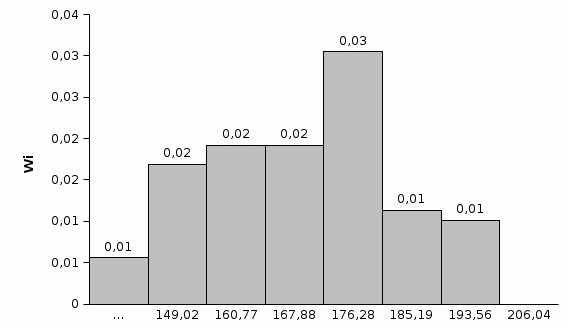 Часть 2. Точечные оценки параметров выборкиТочечные оценки параметров выборки вычисляем по данным табл. 4. Выборочное среднее Хв=(∑nixi) / n. Xв=174,27 Выборочная дисперсия Dв=(∑ni(xi-xв)2)/n. Dв=224,7 Выборочное среднее квадратичное отклонение Ϭв=√Dв . Ϭв=√224,7=14,98 Исправленная выборочная дисперсия S2=n* Dв/(n-1). S2= 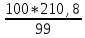 =226,97 =226,97Исправленное выборочное среднее квадратичное отклонение S=√s2=√226,97=15,06
Часть 3. Проверка статистических гипотез.Используем данные выборки (вариационный ряд в третьем столбце табл. 5). Проверить гипотезу о нормальном распределении генеральной совокупностипри уровне значимости 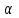 = 0,05. = 0,05.Данные для разделов 3 и 4 берём из исходных данных (табл. 1), ограничившись первыми 20 числами (табл. 5). В качестве нулевой (основной) гипотезы Н0 примем предположение о нормальном распределении генеральной совокупности при уровне значимости 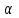 = 0,05. = 0,05.Вычислим выборочную среднюю Хв* и среднее квадратичное отклонение σ*, причём в качестве варианта хi берём середины интервалов xi ср = (xi + xi+1*)/2. Результаты сведены в табл. 6 Таблица 5
Таблица 6
хв*=(∑ Хi ср*ni*)/20 = 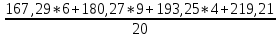 = 180,92 = 180,92σ*=√(∑(xiср*xв)2ni*)/20)= 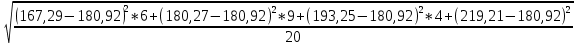 =12,63; =12,63;От случайной величины Х перейдём к стандартной случайной величине Z из N(0,1), сдвинув математическое хв в начало координат и пронормировав по σ к единице: zi = (xi ср*-xв*) / σ*; i = 1, 2, 3, 4, 5; при этом полагаем z1 = -∞, a z7 = ∞. Результаты сведены в табл. 7 Таблица 7
Вычислим теоретические частоты в предположении, что Z нормальная случайная величина. ni 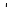 = nPi, где n – объём выборки (в рассматриваемом случае n = 20), = nPi, где n – объём выборки (в рассматриваемом случае n = 20),Pi = Ф(zi+1) – Ф(zi), вероятность попадания Х на интервал (xi*, xi+1*) или Z на (zi, zi+1), а Ф(zi) – функция Лапласа (её значения определяются по справочным таблицам). Результаты вычисления сведены в табл. 8. Таблица 8
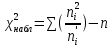 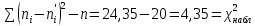 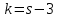 – число степеней свободы – число степеней свободы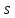 – число интервалов – число интервалов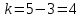 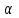 = 0.05 – уровень значимости (по условию) = 0.05 – уровень значимости (по условию)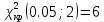 – критическая точка правосторонней критической области (Приложение №5) – критическая точка правосторонней критической области (Приложение №5)4,35 < 6,0 Часть 4. Интервальные оценки параметров нормального распределения случайной величиныВ табл. 9 второй столбец это первые 20 чисел выборки, заданной в табл. 1, третий столбец получен упорядочением выборочных данных, записанных во втором столбце. Таблица 9
Найдём доверительный интервал для оценки математического ожидания при неизвестном среднем квадратичном отклонении с надёжностью 0,95. Согласно формуле (2) при объёме выборки n = 20 и надёжность γ = 0,95 , нужно найти выборочное среднее хв и исправленное квадратичное отклонение s Хв=(∑xi*ni )/n =180,345 Dв=(∑ni(xi-xв)2)/n. Dв=199,79 D≈ S²=(n/(n-1))*Dв= 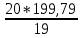 =210,3 =210,3S=√s2 = 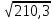 = 14,5 = 14,5По справочным таблицам для n = 20 и γ = 0,95 находим tγ: tγ = 2,09. Тогда доверительный интервал для математического ожидания а равен xв-t γS/√n< a < xв+tγ S/√n или 180,345-(2,09*14.5) /√20 33,56 Найдём доверительный интервал для оценки среднего квадратичного отклоненияϬ с надёжностью 0,95. Согласно формуле (11) при объёме выборки n = 20 и надёжность γ = 0,95, S(1-q) <Ϭ< S(1+q) (q<1) Значение q находим из справочных таблиц: q = 0,37. Тогда доверительный интервал для среднего квадратичного отклонения Ϭ равен 14,5*(1-0,37) <Ϭ <14,5*(1+0,37); 9,135<Ϭ <15,87 Вывод: Так как χ2набл < χ2кр, делаем вывод о том, что данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности. Гипотеза H0 подтверждается. ЗаключениеВ данной курсовой работе было произведено статистическое исследование случайной величины. И выполнены ряд задач, которые научили работать со статистическими данными. Результатом выполнения курсовой работы стало получение навыков, которые помогают применять знания для решения конкретных практических задач, производства расчетов, программирования, также самостоятельно проводить научное исследование и обосновывать применяемые решения. А так же проделанная работа научила высчитывать размах и объем выборки, строить вариационный ряд, строить графики эмпирической функции распределения, полигон частот, полигон относительных частот, гистограмму частот, гистограмму относительных частот, находить доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения, проверять статистические гипотезы, используя критерии Стьюдента и Пирсона. Список использованной литературы:Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В.Е. Гмурман. – 9-е изд., стер. – М.: Высш. шк., 2003. С81-209.: ил. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

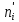 =
=