stroymekh4 Кокурин 19. Стержень элемент, у которого один размер (длина) много больше двух других 2) оболочка
 Скачать 7.44 Mb. Скачать 7.44 Mb.
|
15.Теорема о действительной и возможной работеРабота силы на соответствующем этой силе действительном перемещении, вызываемом той же силой, называется действительной работой. Рассмотрим упругую систему, находящуюся под воздействием системы сил Р1 , Р2 , … Рn , которые вызовут ее деформации и перемещение точек 1, 2, … n (рис.1.1). Эти перемещения представляют собой проекции истинных перемещений соответствующих точек на линии действия нагрузок. Будем считать, что все заданные силы прикладываются статически, т.е. их значения нарастают от нуля до максимальных значений настолько медленно, что они не вызывают ускорений точек системы, а значит и инерционных сил. В условиях идеальной упругости работа этой системы сил не зависит от порядка приложения нагрузок и определяется только их окончательными значениями. Будем считать, что все нагрузки Рn изменяются пропорционально одному параметру и соотношение между ними не меняется. Тогда действительная работа на соответствующем перемещении может быть определена по теореме Клайперона: 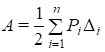 Работа силы на соответствующем перемещении, но вызываемом иной силой или другими факторами, называется возможной или виртуальной работой. Возможная работа определяется по формуле: 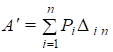 где i n - перемещение точки приложения "i"-той силы, вызванное силой "n". где i n - перемещение точки приложения "i"-той силы, вызванное силой "n".Теорема взаимности работ и перемещенийДля доказательства данной теоремы используется принцип независимости действия сил. Рассмотрим произвольную линейно-деформируемую систему в двух различных состояниях, под действием двух различных нагрузок. Для упрощения выкладок возьмем балку, нагруженную в обоих состояниях самой простой нагрузкой - силами F и F2 (рис. 69). Вначале приложим к балке силу Fj, а затем, к уже деформированной балке, приложим силу F2. В результате последовательного действия этих сил балка изогнется. Отметим, какие перемещения при этом возникают: Ап - перемещения по направлению силы F], вызванные действием силы F A2i - перемещения по направлению силы F2, вызванные силой F Д|2 - перемещения по направлению силы Fu вызванные действием силы F2; Д22 - перемещения имеющие место по направлению второй силы F2, вызванные действием самой силы F2. В обозначении указанных коэффициентов прослеживается следующая закономерность - первый индекс указывает направление, по которому происходит перемещение, а второй индекс говорит о том, какой силой это перемещение вызвано. 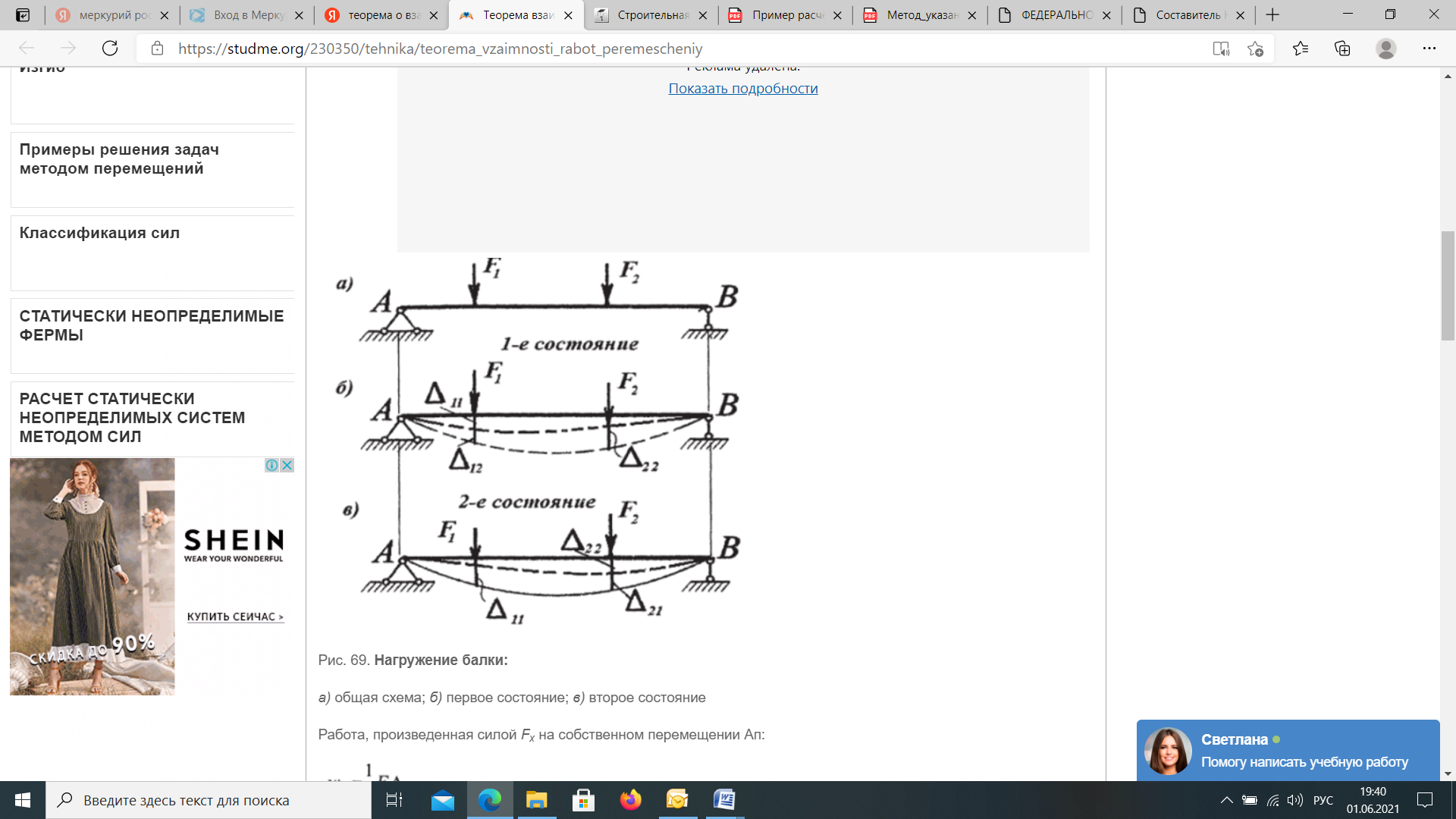 а) общая схема; б) первое состояние; в) второе состояние Работа, произведенная силой Fx на собственном перемещении Ап: Работа, произведенная силой F2 на собственном перемещении Д22* Дополнительная работа Wj2 силы F на перемещении Д12, вызванном силой F2: Здесь множитель /2 отсутствует, т. к. сила Fx на перемещении Д|2 совершав!' работу, оставаясь постоянной. Тогда полная работа, совершенная внешними силами F и Fi при первом способе нагружения: Нагрузим теперь балку в другой последовательности. Вначале приложим силу F2, а затем Ft. Работа, произведенная силой F2 на собственном перемещении Д2г: Работа, произведенная силой F на собственном перемещении Дц: Дополнительная работа w2), произведенная силой F2 на перемещении Д21: Как видим, множитель 'А отсутствует, т. к. сила F2 на перемещении Д2] совершает работу, оставаясь постоянной. Полная работа, совершенная внешними силами F, и F2 при втором способе нагружения: Сопоставим полную работу внешних сил при первом и втором способах нагружения: W) = wM. Следовательно, работа сил не зависит от порядка их приложения. Отсюда получаем: Работа силы Ft на перемещениях, вызванных второй силой F2, равна работе силы F: на перемещениях, вызванных силой Ft (теорема взаимности работ или теорема Бетти). Принимая F2 = F2 = 1, получаем Д12 = Дгь Данное выражение носит название теоремы о взаимности перемещений (теоремы Максвелла). Формулируется она так: перемещение тонки приложения первой силы по ее направлению, вызванное действием второй единичной силы, равно перемещению точки приложения второй силы по ее направлению, вызванному действием первой единичной силы. Теорема о взаимности единичных перемещений. Теорема Максвелла - это теорема о взаимности работ для частного случая нагружения системы, когда F1=F2=1. Очевидно, что при этом δ12=δ21. Перемещение точки первого состояния под действием единичной силы второго состояния равняется перемещению точки второго состояния под действием единичной силы первого состояния. 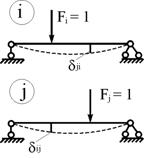 16. Рассмотрим балку, находящуюся под действием произвольных нагрузок (рис. 10.7, а). Назовем состояние балки под действием заданных нагрузок грузовым или действительным состоянием. Допустим, требуется определить прогиб балки в некоторой точке С. Приложим в этойточке по направлению искомого перемещения единичную силуР{ — 1, то есть создадим единичное или вспомогательное состояние (рис. 10.7, б). 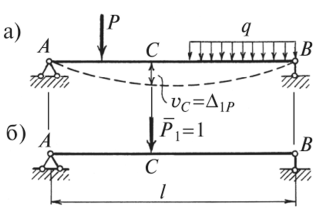 Рис. 10.7 Примем следующую последовательность нагружения: вначале действует единичная сила, а затем заданная нагрузка. Определим работу постоянной по величине единичной силы на перемещении по ее направлению от действия заданных нагрузок, то есть на искомом перемещении точки С. На основании теоремы Бетти она равна Выражая работу Л]р с помощью (10.8) через внутренние усилия в балке в единичном и грузовом состояниях, получаем формулу для определения искомого перемещения:
|