stroymekh4 Кокурин 19. Стержень элемент, у которого один размер (длина) много больше двух других 2) оболочка

• Название: Стержень элемент, у которого один размер (длина) много больше двух других 2) оболочка
• Дата: 10.10.2022
• Размер: 7.44 Mb.
• Имя файла: stroymekh4 Кокурин 19.docx
• Тип: Документы; #726177
• страница: 3 из 3

Если в результате вычислений величина А_кр оказалась положительной, то направление перемещения совпадает с направлением действия единичной нагрузки, а если отрицательной, то оно противоположно этому направлению.

Отметим, что в общем случае нагружения стержня или стержневой системы формула Мора содержит шесть членов (интегралов) по числу внутренних усилий в поперечных сечениях стержня.

Для систем, стержни которых работают на растяжение или сжатие (например, для ферм), отличен от нуля только один член формулы Мора: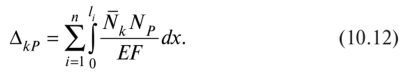 

При расчете балок и стержневых систем, работающих в основном на изгиб (например, рам), влияние поперечных и продольных сил на перемещения несущественно и в большинстве задач не учитывается. Поэтому в формуле Мора можно с достаточной степенью точности использовать только слагаемое, содержащее изгибающие моменты: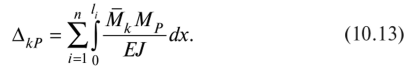



В случае пространственной работы стержня или стержневой системы, элементы которой работают в основном на изгиб и кручение, в формуле Мора обычно используются слагаемые, содержащие изгибающие и крутящие моменты.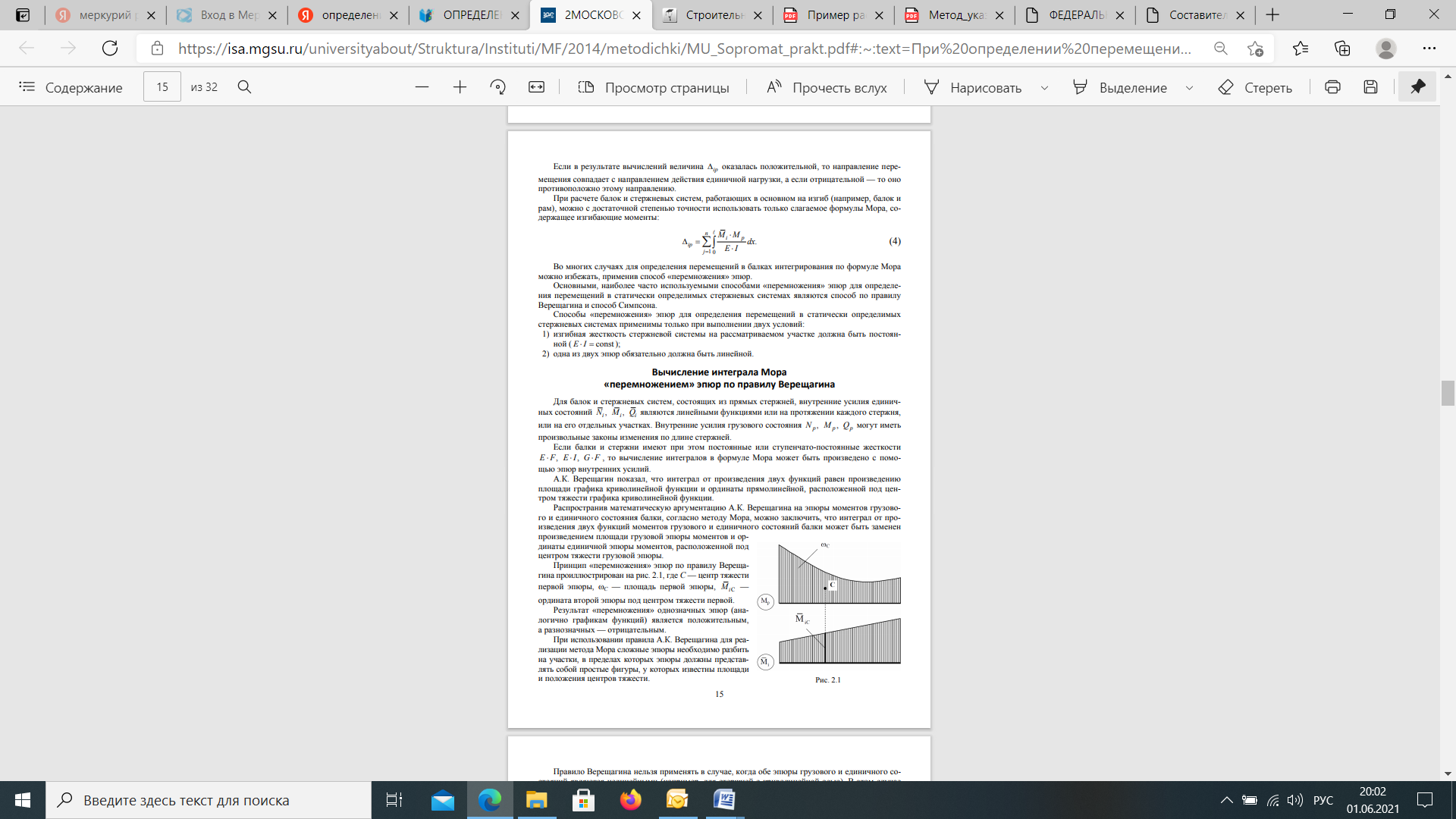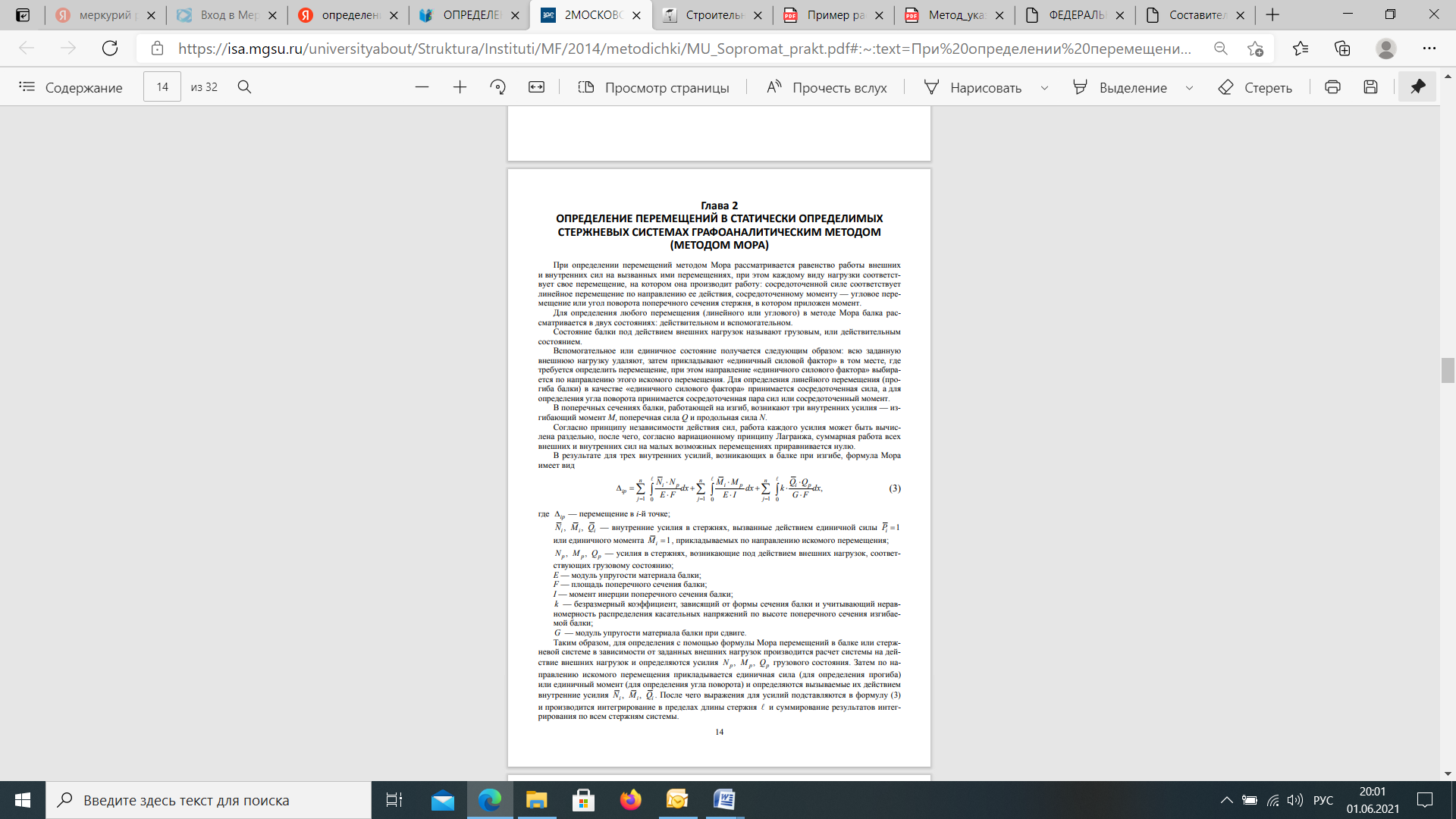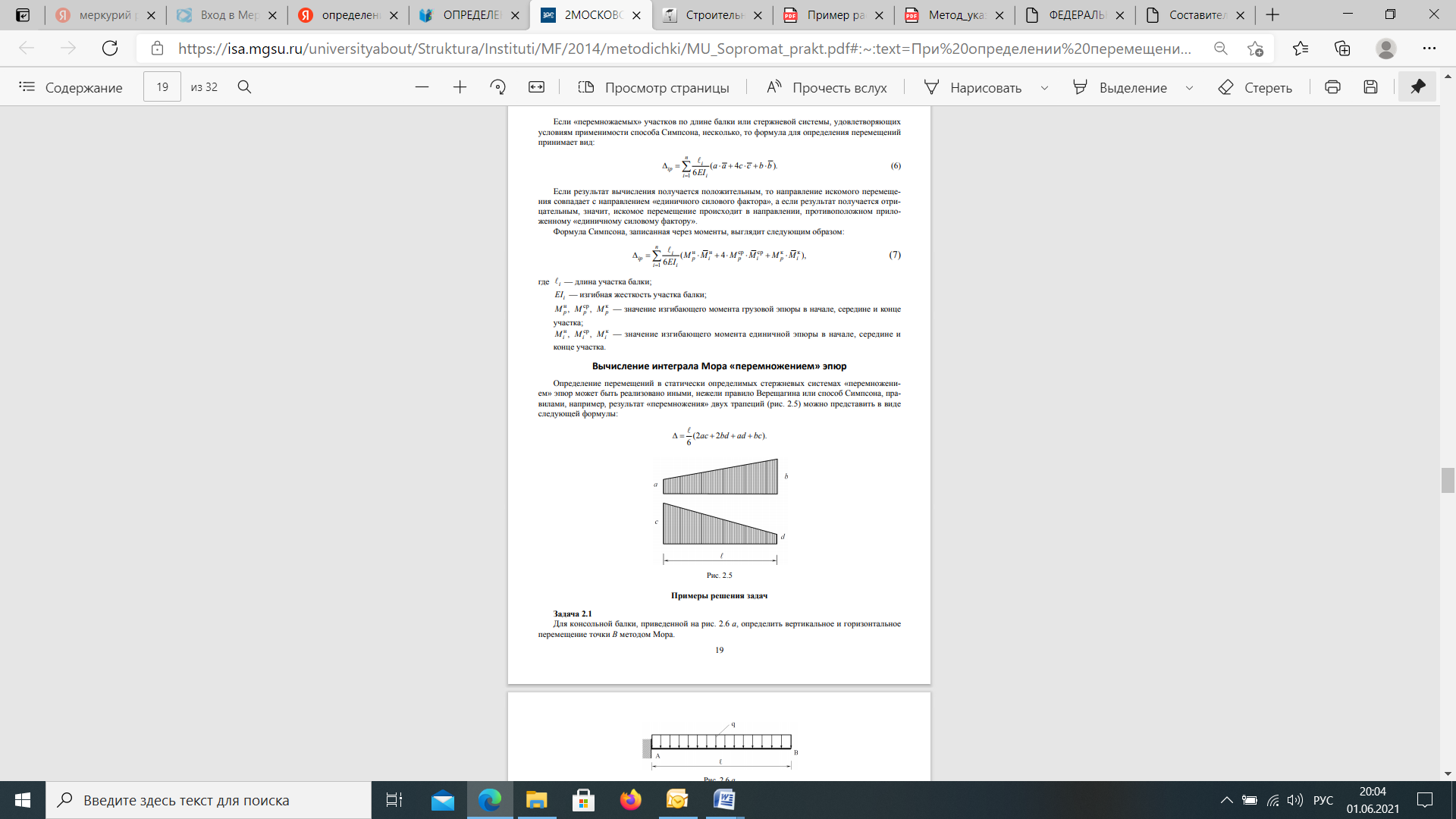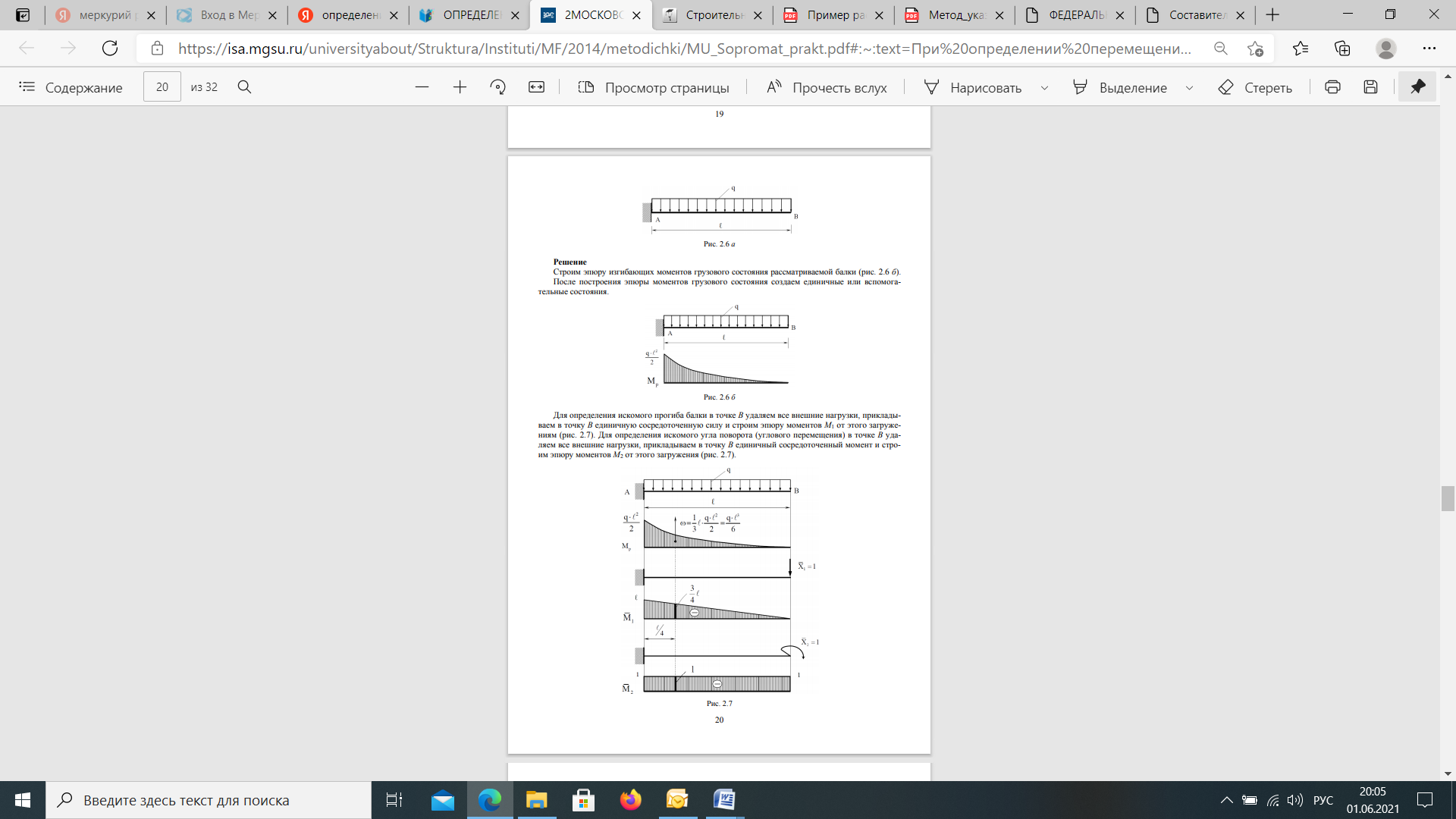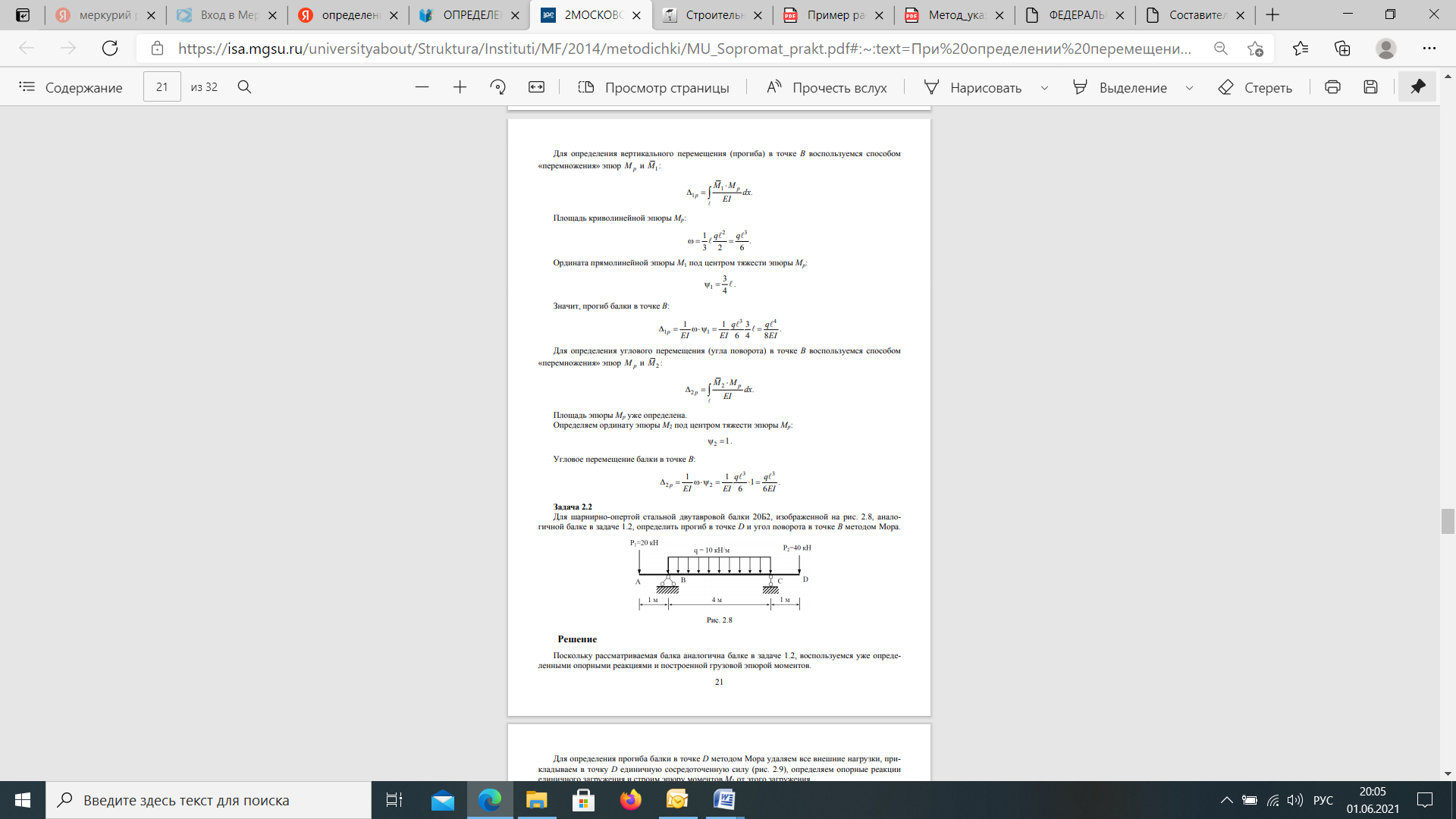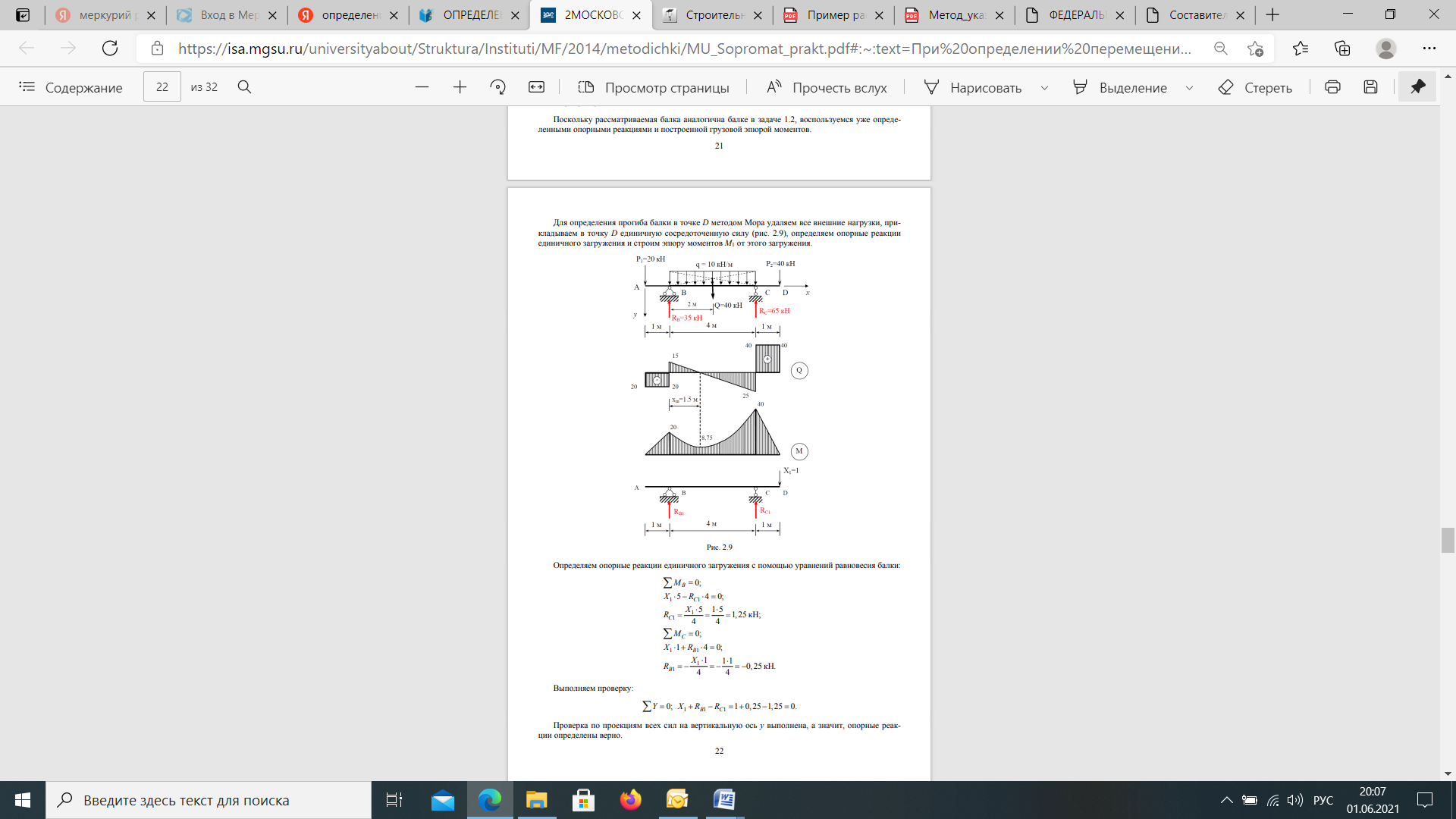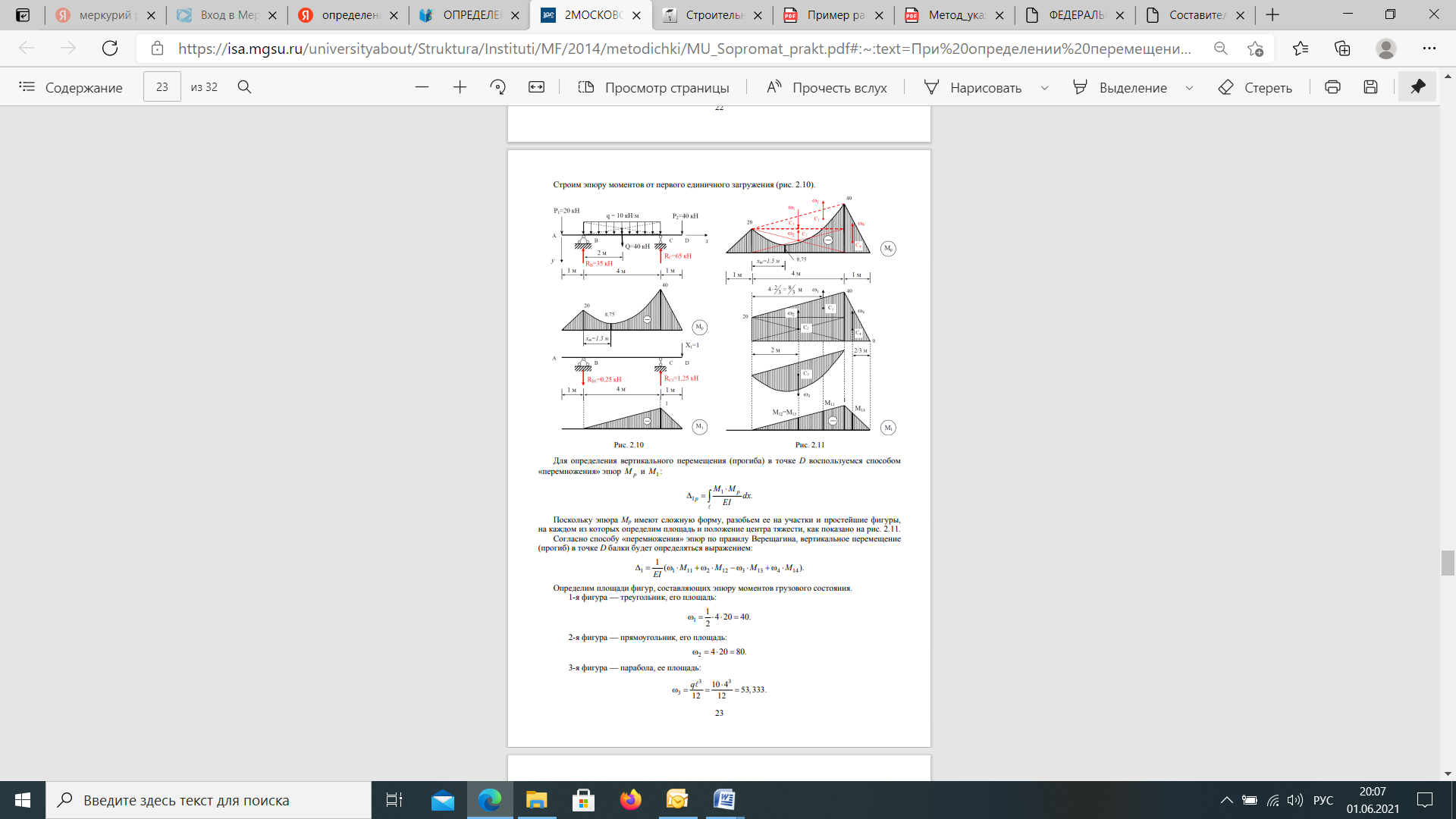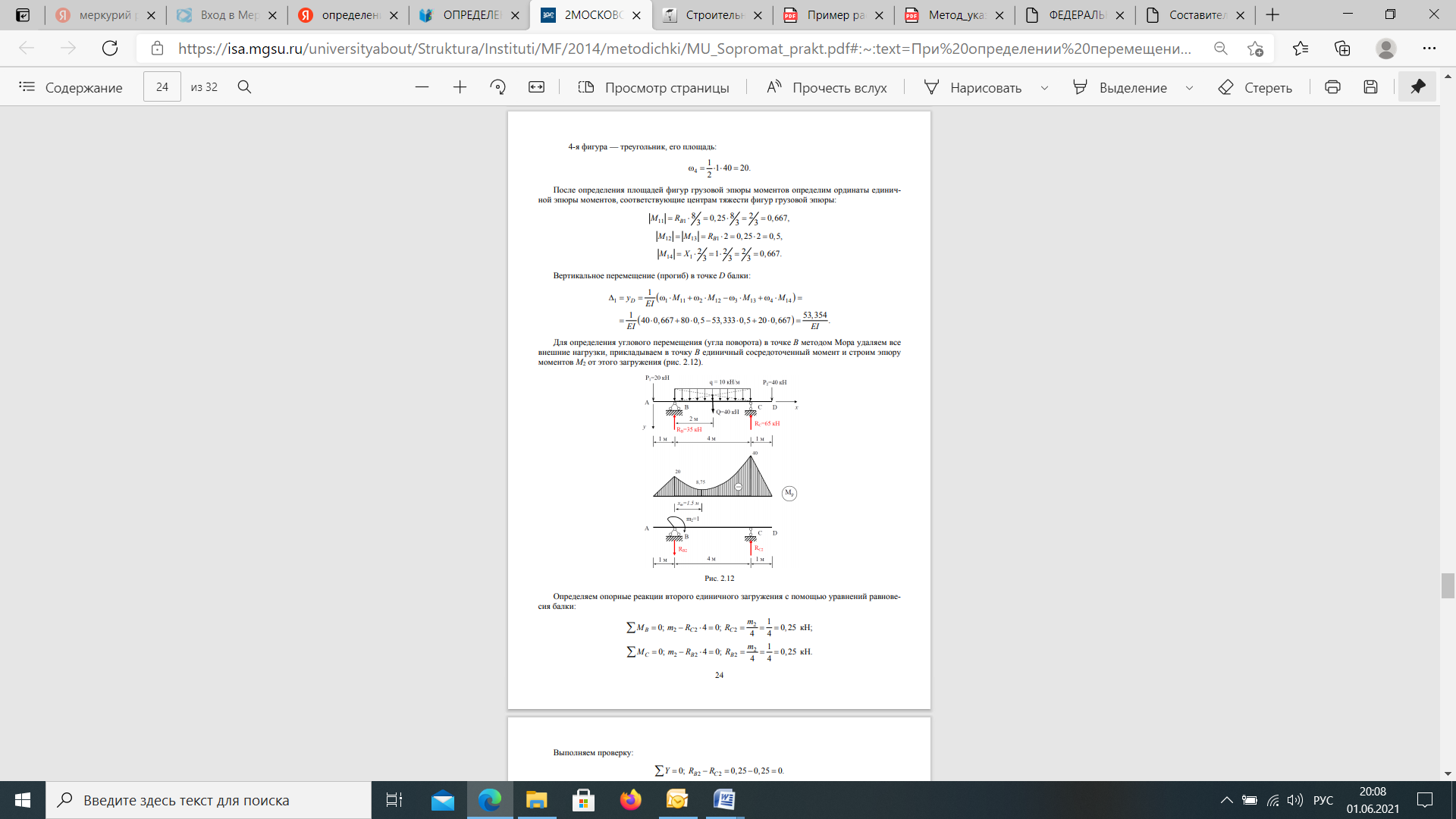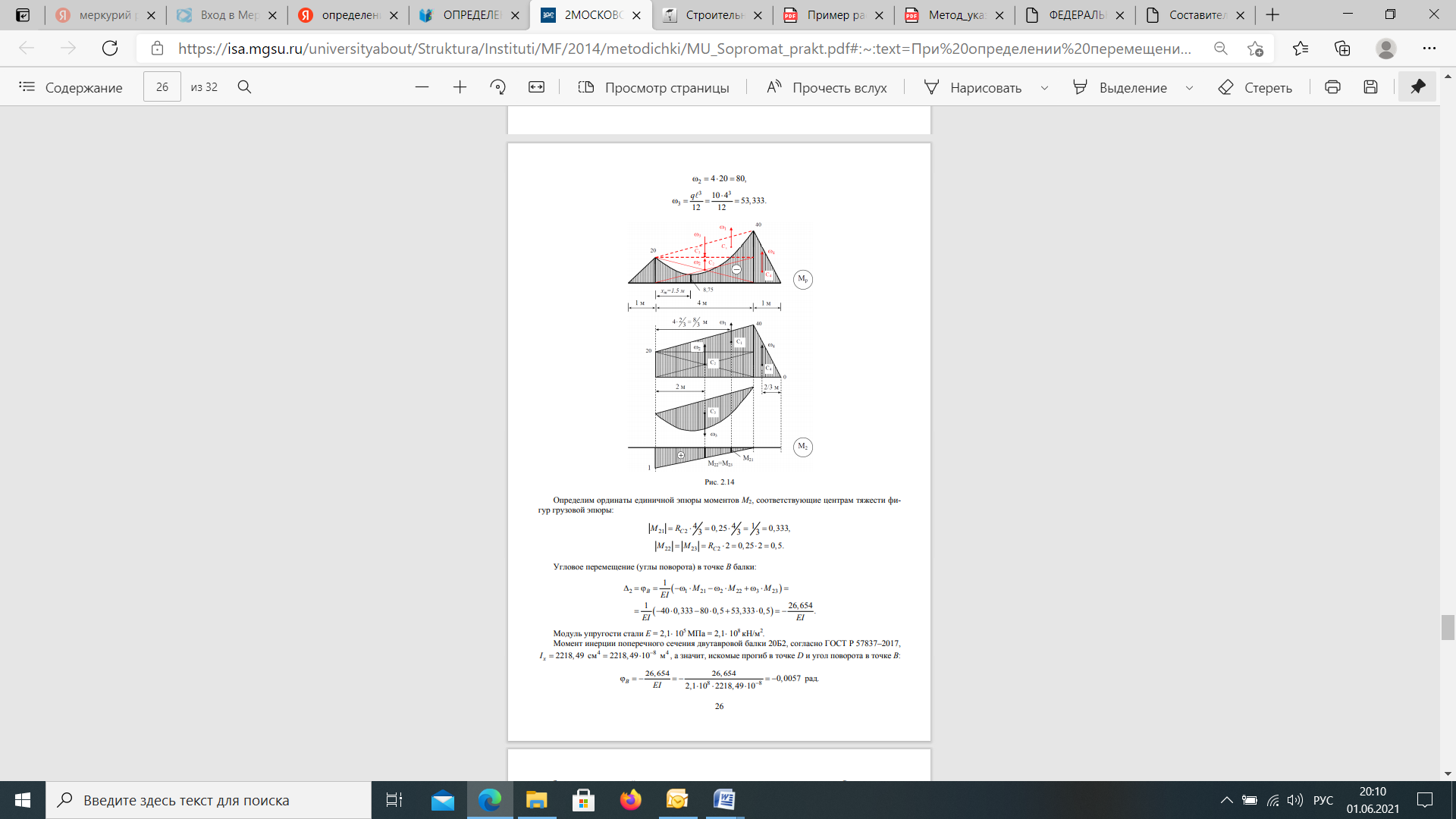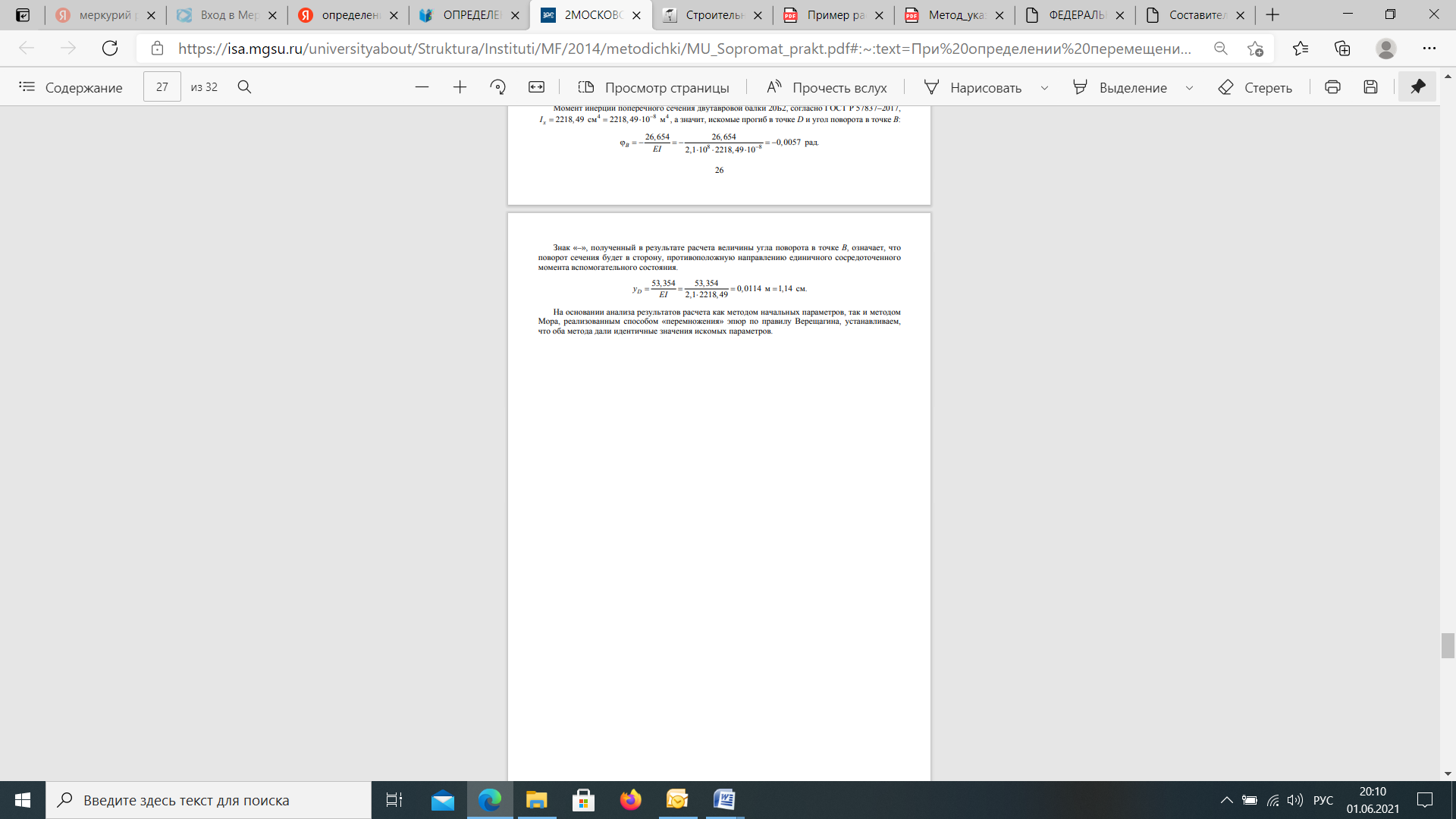




















18. При тепловом воздействии любой материал изменяет форму. Поэтому необходимо различать деформации от силового и теплового воздействий.

При силовом воздействии на плоские расчетные схемы имеют место изгиб и растяжение (сжатие) . При тепловом воздействии происходит искривление и удлинение (укорочение).

Последние виды деформаций изменяют только форму элемента, но не вызывают никаких напряжений в расчетных сечениях статически определимых систем.

При расчете на тепловое воздействие учитывается не температура окружающей среды, а ее ожидаемое изменение в процессе эксплуатации сооружения.

С целью упрощения инженерных расчетов вводится допущение о линейном характере изменения температуры но высоте сечения элемента. Зная расположение нейтральной оси стержня, можно заданное изменение температуры разложить на два воздействия: на равномерный и неравномерный нагрев.

Равномерный нагрев характеризуется температурой t°₀ на уровне нейтральной оси стержня п — п и вызывает только удлинение или укорочение стержня.

При этом температура на уровне нейтральной оси в общем случае равна



а при h_x=h₂ = 0,5h

Неравномерный нагрев характеризуется перепадом температур At, вызывающим искривление стержня из-за различия в удлинении волокон по высоте сечения стержня.

Рассмотрим деформации бесконечно малого элемента стержня dr (рис. 12.17) при тепловом воздействии отдельно для равномерного и неравномерного нагрева.

При действии неравномерного нагрева основным показателем искривления является угол Adcp₍ (рис. 12.17, 6) между боковыми гранями элемента, значение которого определяют следующим образом.

Изменение длины крайних волокон по высоте сечения будет равно:

• 
  • для нижних: Adx, = «,/;'dx;
  
• 
  • для верхних: Adx, = a,?"dx.
  

Тогда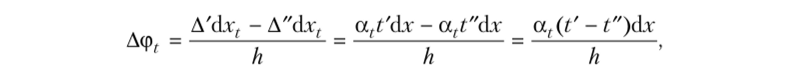



или, так как (t'-t") = At (рис. 12.16), окончательно получим



Для получения формулы определения перемещений от теплового воздействия рассмотрим линейно деформируемую расчетную схему (состояние f) при заданном тепловом воздействии (рис. 12.18, а) и вспомогательное состояние k с приложенной единичной силой по направлению искомого перемещения

Для состояния k применим принцип возможных перемещений (12.15), приняв для него в качестве возможных перемещения состояния f.

Возможная работа внешних сил равна





где a_t — коэффициент линейного расширения материала стержня.

Возможная работа внутренних сил для плоской стержневой системы определяется выражением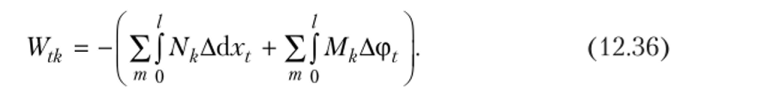



Подставив в (12.36) выражения деформаций от теплового воздействия (12.33) и (12.34) и вынося за знаки интегралов постоянные множители, не зависящие от интегрирования, получим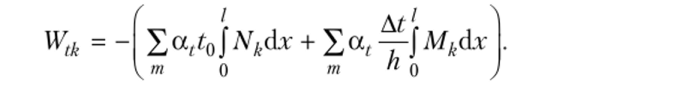



В полученном выражении величины, стоящие под знаками интегралов,

представляют собой площади эпюр N_k и М_к.

Обозначив Qy_k = J N_kdx и =$M_kdx, получим окончательное выражение для возможной работы внутренних сил: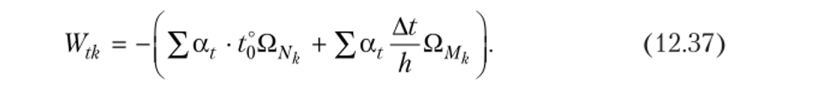



Подставив (12.35) и (12.37) в (12.15), получим формулу для определения перемещений от температурного воздействия: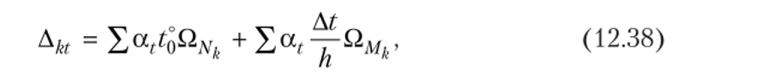



для которой применимо следующее правило знаков.

Каждый член формулы (12.38) при вычислении по участкам будет положительным при совпадении характера деформации от теплового воздействия (растяжения с удлинением или изгиба с искривлением) с характером деформации от единичной силы вспомогательного состояния.

Для первого члена формулы (12.38) знак может быть получен автоматически, если при вычислении значения ?q и N_k подставлять со своими знаками.

Пример. Рассмотрим пример определения перемещения от действия температуры в ломаном стержне (рис. 5.24, а).

Пусть температура^.наружной части контура равна -30°С, а внутри 20°С. Эпюра М_х показана на рис. 5.24, б, а эпюра N_x — на рис. 5.24, в. Для всех трех стержней



Найдем площади эпюр: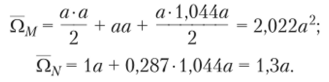



Для определения знаков слагаемых в формуле (5.33) сравним кривизны. Легко заметить, что волокна, расположенные внутри контура, для всех трех стержней от действия температуры удлиняются, а от изгиба силой Р = 1, наоборот, укорачиваются, следовательно, кривизны имеют разные знаки и первое слагаемое формулы (5.33) будет со знаком «минус».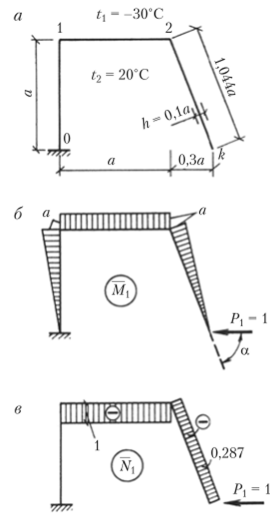



Рис. 5.24

К противоположному выводу приходим относительно знака второго слагаемого. В самом деле, средняя температура (температура оси стержня) для всех трех стержней отрицательная, поэтому стержни укорачиваются, и от силы Р = 1 стержни также укорачиваются, поэтому второе слагаемое будет со знаком «плюс». Таким образом,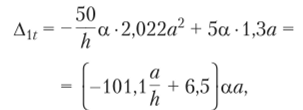



но a/h = 10, поэтому Д₁₍ = -1004,5аа.

Итак, получено отрицательное значение перемещения. Это означает, что перемещение точки k происходит в сторону, противоположную направлению силы Р = 1.

19. В статически определимых стержневых системах смещение опор по направлению опорных связей не вызывает деформацию стержней. Стержни при этом совершают перемещения как жесткие тела. В простых случаях определение перемещений может быть произведено на основании геометрических соображений без использования специальных формул.

Например, вертикальное перемещение точки В балки АС при смещении (осадке) опоры А на величину с (рис. 8.43) легко определяется из пропорции



Для более сложных случаев используется формула, вывод которой можно сделать на основании принципа возможных перемещений или на основании теоремы Бетти о взаимности работ.

Рассмотрим, например, смещения и поворот жесткой заделки статически определимой рамы (рис. 8.44, а). Новое положение стержней рамы показано пунктиром. Деформации стержней отсутствуют.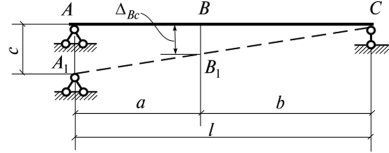



Рис. 8.43

Определим горизонтальное перемещение точки К. Для этого приложим по направлению искомого перемещения единичную силу Р = 1, т.е. создадим единичное состояние (рис. 8.44, б). При этом на смещаемой опоре возникают опорные реакции, которые обозначим Rj (i — номер опорной связи).

Составим выражение для работы сил единичного состояния на перемещениях действительного состояния. Учитывая, что в действительном состоянии нагрузки отсутствуют и работа сил этого состояния равна нулю, на основании теоремы Бетти о взаимности работ запишем: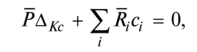



где С/ — компоненты смещения опоры.

Из данного уравнения получаем формулу



В этой формуле произведение R_ic_j представляет собой работу опорных реакций соответствующего единичного состояния на заданных смещениях опор. Это произведение будет положительным, если направления опорных реакций совпадают с направлениями соответствующих смещений опор.

При определении углов_поворота сечений единичное состояние создается моментом М= 1, приложенным по направлению соответствующего углового перемещения.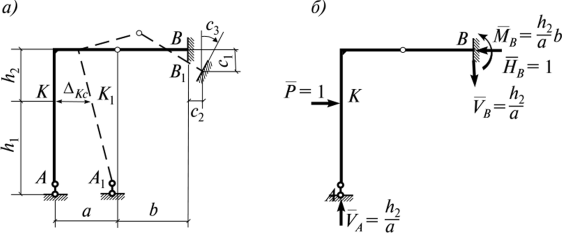



Рис. 8.44

Выполним для рассматриваемой рамы статический расчет в единичном состоянии и определим опорные реакции в жесткой заделке (рис. 8.44, б). По формуле (8.30) находим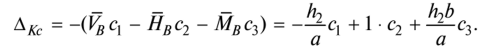



Пример 8.15. Определим вертикальное перемещение точки В шарнирно опертой рамы (рис. 8.45, а) при смещении опор А и Сна величины с_х = 0,02 м и с₂ = 0,01 м.

Приложим в точке В вертикальную единичную силу Р = 1 (рис. 8.45, б) и определим опорные реакции на смещаемых опорах. По формуле (8.30) находим искомое перемещение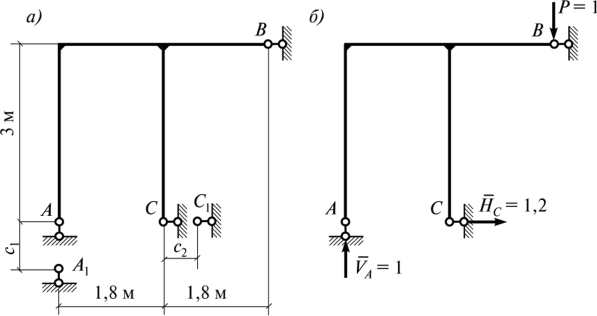

 

Рис. 8.45

Точка В перемещается по направлению действия единичной силы, т.е. вниз.

Пример 8.16. Определим угол поворота жесткого узла В для рамы с промежуточным шарниром при повороте жесткой заделки на величину с_х = 0,02 рад и осадке опоры С на величину с₂ = 0,03 м (рис. 8.46, а).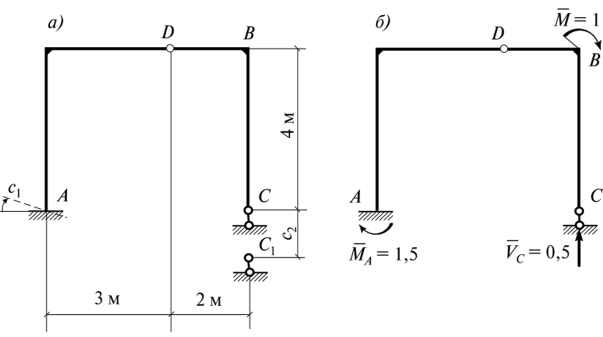



Рис. 8.46

Приложим в точке В момент М = 1 и произведем статический расчет рамы в единичном состоянии. Величины опорных реакций на смещаемых опорах приведены на рис. 8.46, б. По формуле (8.30) находим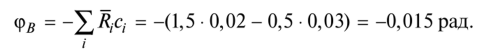



Поворот жесткого узла В происходит против хода часовой стрелки.